远距航空通信变换域通信系统设计

王桂胜，任清华，徐兵政，刘　洋

(1.空军工程大学 信息与导航学院，西安 710077；　2.中国电子科技集团航天信息应用技术重点实验室，石家庄 050081)(*通信作者电子邮箱wgsfuyun@163.com)

0　引言

变换域通信系统(Transform Domain Communication System, TDCS)作为一种典型的战场认知无线电系统，能够主动规避干扰，具有抗干扰、低截获等传输特征，更适合对抗条件下的无人机数据链应用[1-2]。在远距航空通信中，TDCS常面临收发双方电磁频谱环境差距较大的问题，极易导致通信过程中误码率较高，严重影响整体通信质量[3]。因此，研究分析TDCS在远距航空通信下的电磁频谱环境，针对性设计远距航空通信下系统模型对于提升TDCS整体通信性能具有重要意义。

目前，针对TDCS在复杂电磁环境下的研究较多，文献[4]针对频谱不一致下的通信干扰问题，设计了一种基于信令信道的远距离航空型TDCS，能够有效抵抗多音干扰；文献[5]研究了TDCS在收发频谱不一致条件下的基函数设计方法，实现了信噪比(Signal-to-Noise Ratio, SNR)的次优解；文献[6-7]则针对TDCS在幅度谱成型过程中存在的问题，利用功率谱翻转和注水定理对基函数生成进行改进，提高了整体的抗干扰和低截获性能。以上研究主要围绕小范围频谱一致条件下的TDCS进行设计与仿真，没有对远距航空型TDCS通信进行针对性研究。针对不一致信息交互问题，常用的处理方案通常有建立专有信令信道或者直接信息交互。信令信道构造原理简单，但信道利用率低，且在动态、广域等实际应用中受限；而直接信息交互则利用较为复杂的技术和相关算法实现可靠传输，信道利用率高，实际应用较为广泛。

针对这一现状，本文针对远距航空型TDCS通信过程中面临的通信干扰问题，对其电磁频谱环境及典型干扰进行分析建模，基于存储转发模式，设计适合远距航空通信的TDCS模型及通信方案。仿真结果表明，本文建立的远距航空型TDCS模型能够适应收发双方复杂的电磁频谱环境，提出的通信方案与传统TDCS相比，误码率较低，抗干扰性能显著。

1　远距航空通信电磁环境

在远距航空通信过程中，我方通信平台极易受到敌方机载或地面干扰平台强烈的电磁干扰，通信有效范围将主要受收发双方天线位置、电波传输特性及地球曲率等因素影响。如图1所示，机载干扰平台B、C对地面电台A、集群D的干扰效果受到视距传播条件的限制，因此，基于收发双方的相对位置不同，收发两端的频谱感知可能会受到各自周围电磁环境的影响，从而导致双方的频谱感知结果不一致，通信能力下降。

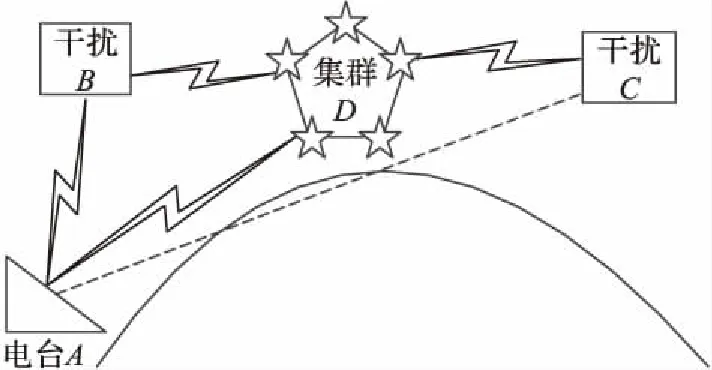
图1　远距航空通信示意图Fig. 1　Schematic diagram of long distance aeronautical communication

1.1　电磁频谱环境分析

在远距航空通信过程中，地面电台和机载电台将面临复杂多变的电磁环境，根据干扰平台的相对位置，对收发双方各自的频谱感知情况作具体分类，见图2。因此，收发双方的电磁频谱感知结果决定着远距航空通信过程中TDCS的整体性能好坏：收发双方频谱一致情况下，通过各自感知结果，实现干扰规避，完成正常通信；在不一致情况下，TDCS收发双方需要交互频谱感知信息，构建性能较优的基函数实现抗干扰通信。

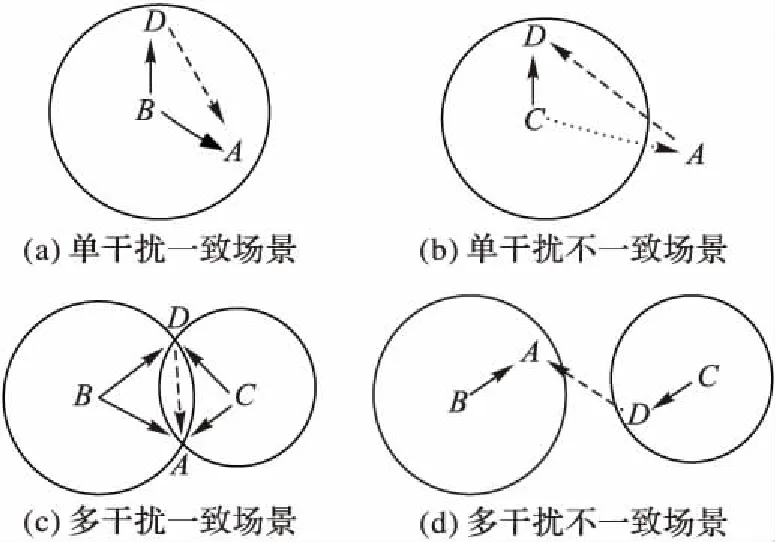
图2　通信电磁频谱环境Fig. 2　Communication electromagnetic spectrum environment

1.2　典型干扰时频特性分析

干扰信号通常包括自然干扰和人为干扰两种[8]。本文主要研究人为干扰，按照频率特性可分为单音、多音、部分频带干扰及线性调频干扰等，具体分类模型如下：

单音干扰是针对某一特定的频点的干扰，其干扰模型为：

J(n)=J0cos(2nπf0+θ0)

(1)

多音干扰由多个单音干扰组成，能同时对多个频点进行干扰，其数学模型为：

(2)

部分频带干扰又称为窄带干扰，主要以瞄准式干扰和阻塞式干扰[9]为主：瞄准式干扰通常围绕某一特定频率，干扰辐射频带较窄，见图3；阻塞式干扰(以梳状谱干扰为例)中各干扰在频域间断输出，干扰频带呈梳形，见图4。由于实际干扰常以瞄准式干扰和梳状谱干扰为主，故本文重点对这两种干扰进行TDCS性能分析。

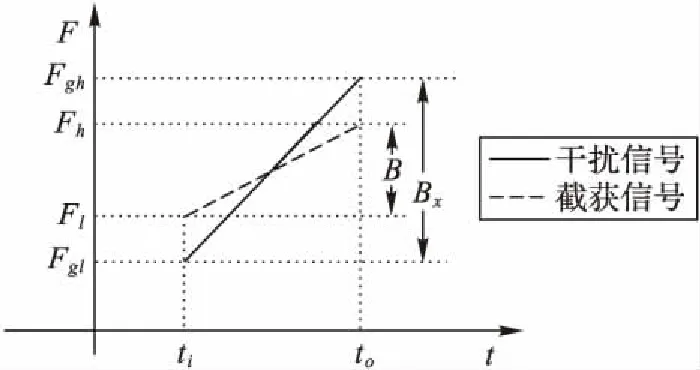
图3　瞄准式干扰时频关系Fig. 3　Time-frequency of spot jamming

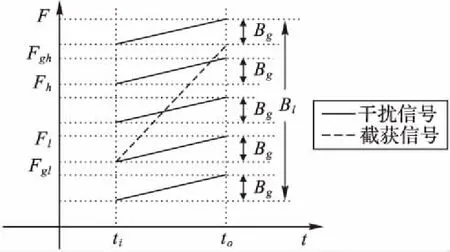
图4　梳形阻塞式干扰时频关系Fig. 4　Time-frequency of comb jamming interference

2　远距航空通信下的TDCS模型

目前，TDCS通信技术研究主要针对系统单个模块或关键技术，但对特定应用场景下的系统研究和整体实现相对匮乏，加之收发两端频谱感知信息的获取较为方便，对其频谱是否一致的判决可直接进行频谱信息比较或者利用对应基函数进行相关运算，通过相关性能的比较可判别[10-12]。针对远距航空通信过程中可能面临的复杂电磁环境及收发双方存在的频谱不一致现状，需要在传统TDCS基础上进行改进，通过收发双方的信息交互，设计适合远距航空通信下的TDCS模型，从而实现安全可靠的信息通信。

2.1　频谱一致条件下TDCS

频谱一致条件下TDCS通过收发双方联合进行空闲频谱感知，从而达到躲避干扰的目的，实现军事航空通信的抗干扰。TDCS发射机和接收机原理分别如图5、6所示。

TDCS发端首先对周围电磁环境进行频谱感知，得到基函数幅度谱Ak，然后利用循环移位寄存器产生伪随机序列，并经相位映射产生随机相位ejθ，从而生成基函数Bk：

Bk=Akejθk

(3)

经傅里叶逆变换后得到基函数的时域形式bn：

(4)

并利用该基函数对产生的随机信号fn进行常用的循环码移键控(Cyclic Code Shift Keying, CCSK)调制，得到发射信号sn：

(5)

其中:c代表功率调整因子，mi代表第i次发送的数据。

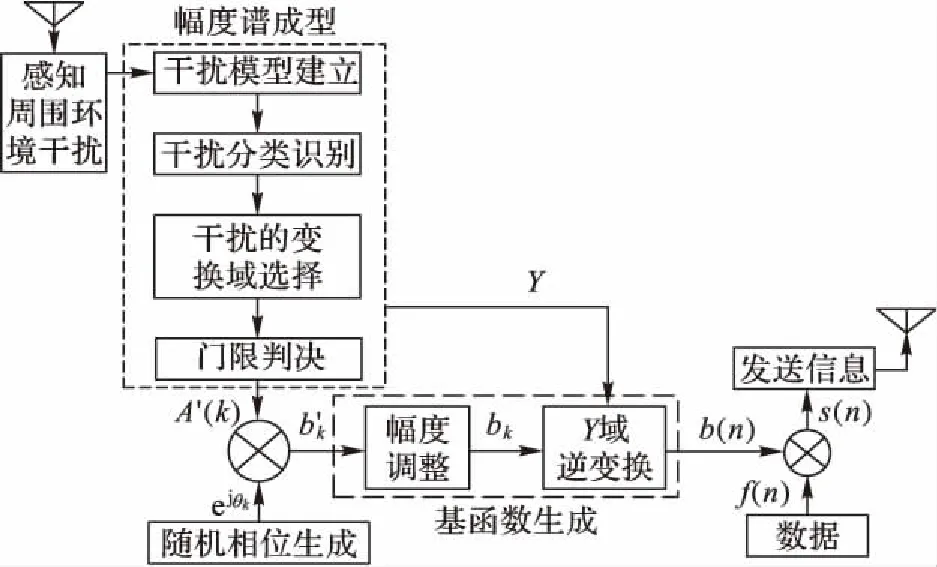
图5　TDCS发射机原理图Fig. 5　Schematic diagram of TDCS transmitter

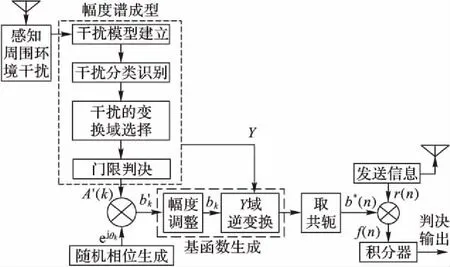
图6　TDCS接收机原理图Fig. 6　Schematic diagram of TDCS receiver

发射信号后经高斯白噪声信道传至接收端，则接收信号rn为：

rn=sn+jn+zn;n=0,1,…,N-1

(6)

其中：zn是均值为0、方差为N0/2的高斯白噪声；jn为接收端干扰。

考虑到收发双方频谱基本一致，收端仍对周围环境进行频谱感知生成自身基函数，利用基函数共轭形式进行近似相关接收处理，从而得到解调信号：

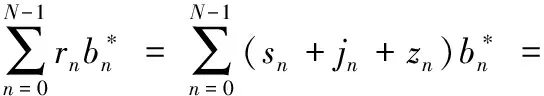
(7)

由于收发双方的频谱感知结果基本一致，接收端基函数幅度谱在对应的干扰各频点处全为0，故∑JkAk≈0，再通过门限判决输出即可消除噪声的影响，从而保证传输信号的准确性。

2.2　频谱不一致条件下TDCS

2.2.1系统整体设计

频谱不一致条件下TDCS需要通过收发两端的相互交互来实现安全可靠通信。为满足通信的时效性，通信双方应尽量保证全双工工作方式(收发可同时进行通信，以保证双方能在较短时间内交互信息)。期间，收发两端的基函数生成模块生成各自的基函数，而存储转发模块用于将发(收)端传递的基函数进行调制或恢复处理，从而实现简易可靠的基函数安全传输。TDCS原理如图7所示。

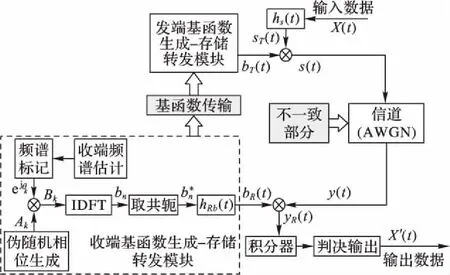
图7　TDCS原理图Fig. 7　Schematic diagram of TDCS

2.2.2存储转发模块

在此情景下，假设收发端通信的平均传播时延τ一定，每组数据通信完成(发送-接收-解调)的时刻为…,ti-1,ti,ti+1,…，即：

ti-1+τ=ti

(8)

令b1(ti-1)、b2(ti-1+τ)和b2(ti)分别表示为ti-1时刻发端生成的基函数、ti-1+τ时刻收端解调发端信息的基函数以及ti时刻收端产生的基函数，则TDCS收发两端的基函数生成-存储转发模块的信息通信流程如图8所示。

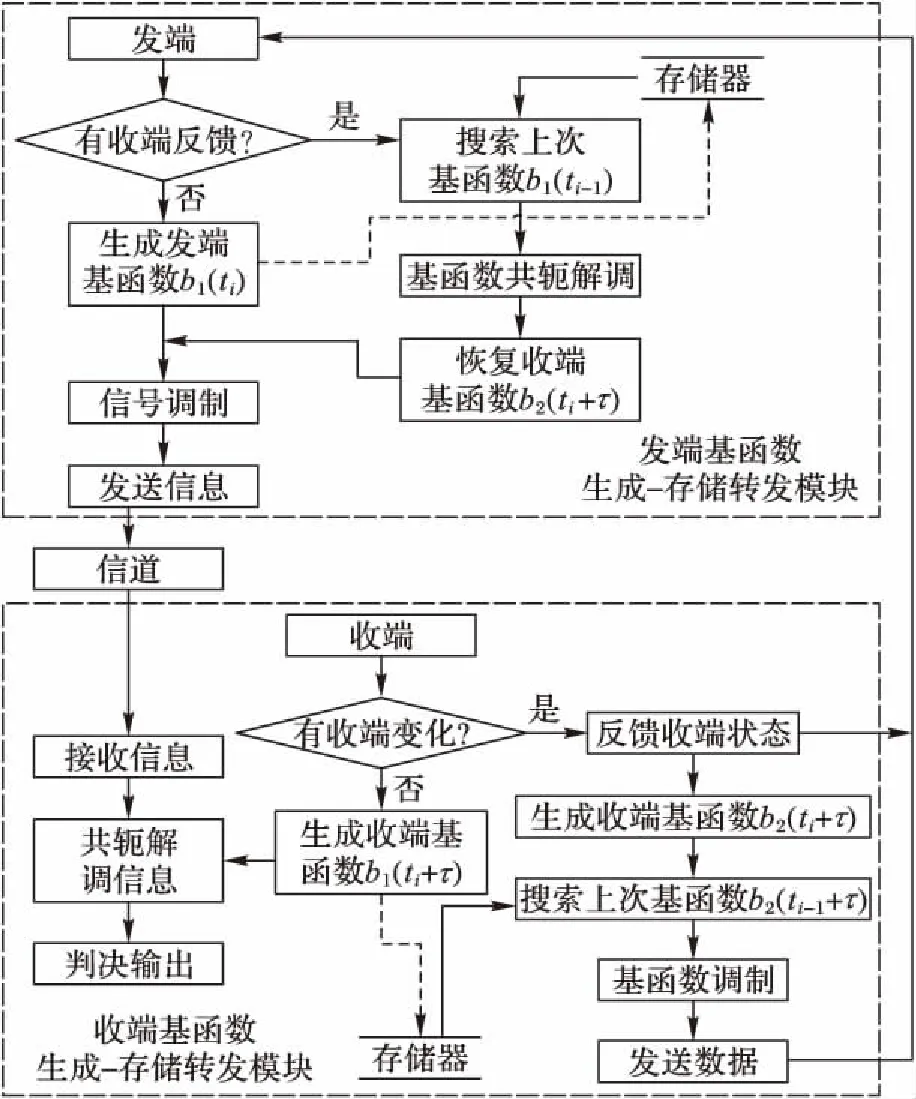
图8　基函数生成-存储转发模块Fig. 8　Basis function generate-store and forward model

步骤1假设在ti-1时刻TDCS收发两端处于频谱一致条件下，仍进行正常通信：

b1(ti-1)=b2(ti-1+τ)=b2(ti)

(9)

步骤2收发两端将各自的基函数b2(ti)、b1(ti-1)进行存储。

步骤3假设在ti时刻收端受到强干扰影响，导致收发频谱不一致，令基函数频谱相同部分为b0(ti)，则

b2(ti-1+τ)=b0(ti)+b1′(ti-1)=

(10)

步骤4收端将自身当前状态反馈给发端，以便下一步发端进行调整。此时，收端反馈信息fb(ti)设定为收发双方的基函数互相关函数：

fb(ti)=b2(ti-1+τ)*b2(-ti)

(11)

由于收发双方的频谱信息有较大程度相似，则反馈信息呈现冲激特性(相关性较强)，再通过相应的采样、量化、编码等步骤实现反馈信息的数字化。

步骤5收端生成新的基函数b2(ti)：

(12)

步骤6收端搜索前一时刻发端发送过来的基函数b2(ti-1+τ)。

步骤7收端利用旧基函数b2(ti-1+τ)将反馈信息和新基函数b2(ti)依次调制成类噪声并发送给发端。

f2(ti+τ)=f2(ti)=

cb2(ti-1+τ)×fb(ti)+j0(ti)+z0(ti)=

(13)

s2(ti+τ)=s2(ti)=

cb2(ti)×b2(ti-1+τ)+j0(ti)+z0(ti)=

(14)

步骤8发端搜索前一时刻基函数b1(ti-1)，利用得到的基函数对接收到的反馈信息进行基函数共轭解调，从而得到反馈信息，并根据其能量检测结果判断收发双发的状态信息：

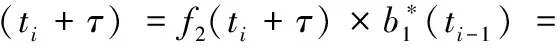
fb(ti)+j0(ti)+z0(ti)]×

(15)

步骤9发端接收到收端的反馈信息后，对收端发送信息进行解调：

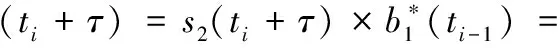
(16)

步骤10恢复出收端的基函数b2(ti+τ)，再利用其重新进行信号调制并发送。

3　性能分析与仿真验证

为验证远距航空通信TDCS模型及其通信流程的合理性，针对远距航空通信电磁环境及典型干扰的时频特性进行仿真实验，并与传统的TDCS模型进行对比。

仿真硬件平台为配置Pentium Dual Core (3.06 GHz)CPU、2 GB内存的计算机，所有实验均在Matlab R2010a环境下进行。仿真中假设信道为高斯白噪声信道，采样速率Fs=512 MHz，采用m序列生成基函数，调制方式采用码移键控(Code Shift Keying, CSK)，干扰信号与基函数幅度谱采用共轭对称频谱，频谱幅度取值参考文献[16]。

本文仿真实验中共选取两种干扰类型作对比，其中:窄带瞄准式干扰选取占频比为25%，干扰频点位置为3/8Fs～5/8Fs；梳状谱干扰选取占频比也为25%，各子带宽为25 Hz。

根据设定的仿真参数，本文分别开展干扰频谱仿真、收发频谱一致TDCS通信及不一致TDCS通信等仿真实验。

3.1　干扰频谱仿真

针对干扰模型的时频特性，结合设定的仿真参数，以窄带和梳状谱干扰为例，得到如图9和图10所示的干扰频谱仿真结果。从图9、10中可以看出，各干扰模型的频谱设定均符合理论分析需要，基本能够满足下一步收发不同频谱场景下TDCS的通信需求。

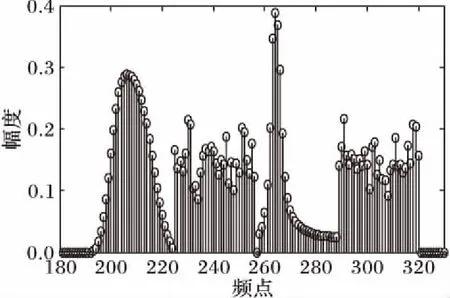
图9　窄带瞄准式干扰模型仿真结果Fig. 9　Simulation result of narrowband spot jamming model

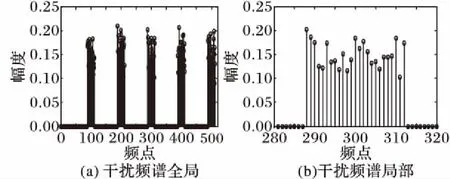
图10　梳状谱干扰模型仿真结果Fig. 10　Simulation result of comb spectrum interference model

3.2　收发频谱一致条件下TDCS性能验证

收发端频谱一致时通信以正常的远距航空TDCS通信为主，干扰类型以窄带干扰为例：通过对基函数的幅值进行设定，利用循环移位寄存器产生m序列，后经相位映射产生随机相位，通过快速傅里叶变换(Fast Fourier Transformation, FFT)逆变换得到基函数的时域形式，并利用该基函数对产生的随机信号进行CSK调制，经高斯白噪声信道传至接收端，利用基函数共轭形式进行相关解调，对比解调后信息与原始信息求得TDCS误码率。初始信息位数为1 000 bit，信干比(Signal to Interference Ratio, SIR)为-3 dB，信噪比为1～12 dB，进行100次蒙特卡罗实验后，其仿真结果如图11所示。从图11中可以看出，在不同干扰下，基函数的类噪声性能良好，且具有较好的自相关性能，便于解调；收发频谱一致条件下TDCS性能与理想误码率比较接近，基本满足远距航空通信的需求。

3.3　收发频谱不一致条件下TDCS性能验证

收发频谱不一致时，TDCS通信主要以受干扰强度较大的接收端频谱为基准构建基函数，然后根据建立的基于存储转发机制的基函数调制解调，进行不一致条件下的通信。此时，干扰的影响主要体现在收发两端频谱不一致部分及其门限判决结果，可能影响因素有：占空比、相似度、频点位置和判决门限等，本文采用较普遍的硬门限判决[4]，仿真参数设置如表1。

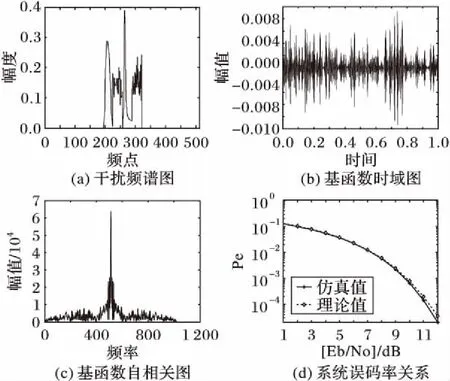
图11　收发端频谱一致时窄带干扰下TDCS性能Fig. 11　TDCS performance in narrowband jamming under the consistent transmit and receive spectrum

表1　收发频谱不一致时的仿真参数设置Tab. 1　Simulation parameters of inconsistent transmit and receive spectrum

将传统TDCS收发各自基函数调制解调通信、通过建立信令信道取收发公共部分建立基函数以及本文提出的基于存储转发机制的基函数调制传递三种方法进行比较，分别在不同占空比、相似度和频点位置进行系统性能的仿真实验，得到如下仿真结果。

3.3.1时延分析

本文提出的基于存储转发模块的远距航空通信TDCS模型的关键模块(存储转发)在频谱一致条件下与传统TDCS模型基本类似，各类性能差距较小，可作近似处理；而在频谱不一致条件下，其存储转发机制的作用愈发突出，故本节主要在频谱不一致条件下进行算法的时延分析。

不一致条件下TDCS的时延分析从频谱感知开始分为两个阶段：基函数生成阶段(幅度判决—随机相位生成—基函数逆变换)和信号处理阶段(信号调制—信道传输—相关解调)，最终实现信号的发送与接收过程。由于基函数处理阶段不涉及信噪比的变化，且与信号长度无关，故不对其进行分析，主要比较信号处理阶段的时延性能。

仿真中初始信号长度范围为100～500 bit，信噪比范围为8～12 dB(误码率低于10-2)，由于信号处理阶段随着信号长度的增加其时延会急剧增长，不便于数据表示，故对原始数据作进一步处理，采用时延率vt(单位：s/bit)来表征其延时性能，具体仿真结果如图12所示。由图12可以看出，本文设计的TDCS模型比信令信道传输模型的时延率受信噪比的影响较小，可近似忽略其影响；同时由于信令信道需要提前建立安全可靠的信道，成本较高，信道利用率较低，而本文设计的TDCS模型比信令信道传输模型时延略长，增加仅约20%，由于TDCS具有宽带、高速传输特性，通过牺牲部分开销来保证信息的可靠传输，具有一定的实用价值。

图13是信噪比范围内平均时延率与信号长度的关系，可以看出：平均时延率随信号长度的增加而增加，基本呈线性增长关系，因此在通信过程中应控制数据分组的长度，以保证在时延可接受的范围内提高信道利用率。

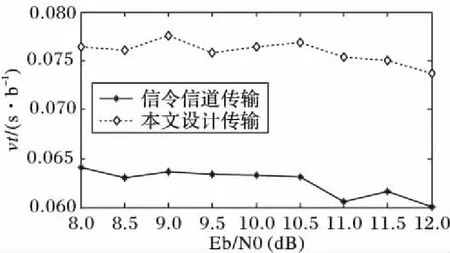
图12　500 bit下时延率与信噪比关系Fig. 12　Relationship of time delay rate and SNR with 500 bit signal

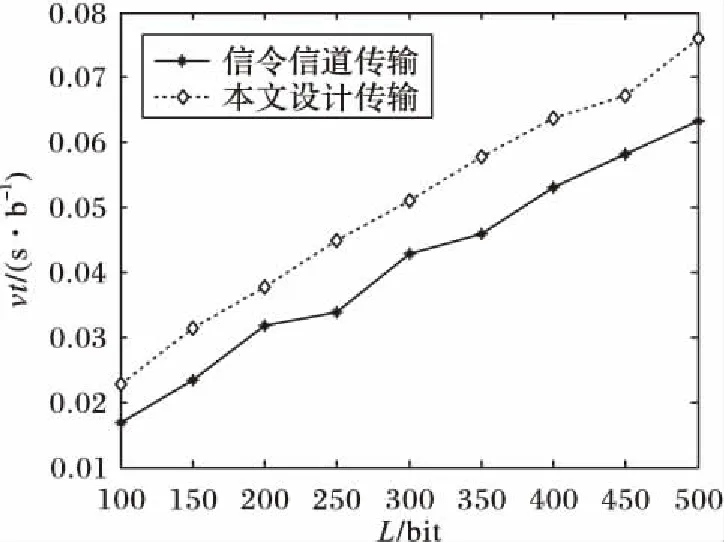
图13　平均时延率与信号长度的关系Fig. 13　Relationship between average time delay rate and signal length

3.3.2性能分析

如图14～16所示，通过对比发现：由于梳状谱干扰的干扰频点较集中，因而收发两端的基函数自相关及其互相关性能较好；本文提出基于存储转发机制的不一致条件下TDCS通信误码率与建立信令信道的通信方式基本相同，较传统的TDCS通信误码率有较大程度降低，在信噪比1～12 dB范围内，误码率平均降低24.48%，相同误码率下性能提升约1 dB，且随信噪比的增加，性能提升越明显。

4　结语

本文从远距航空型TDCS面临的通信干扰问题出发，对不同电磁频谱环境分析建模，提出了远距航空型TDCS模型及通信流程，改善了应对复杂电磁环境的系统性能。仿真表明，在不同干扰条件下，本文建立的干扰模型与频谱设定基本满足复杂电磁环境的理论分析需求，提出的远距航空型TDCS模型相比传统TDCS具有较低的误码率。

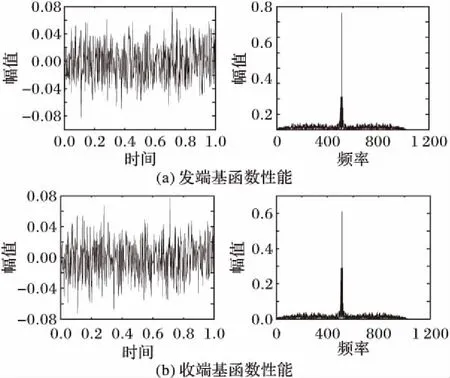
图14　收发端基函数性能Fig. 14　Basic function performance of transmitter and receiver

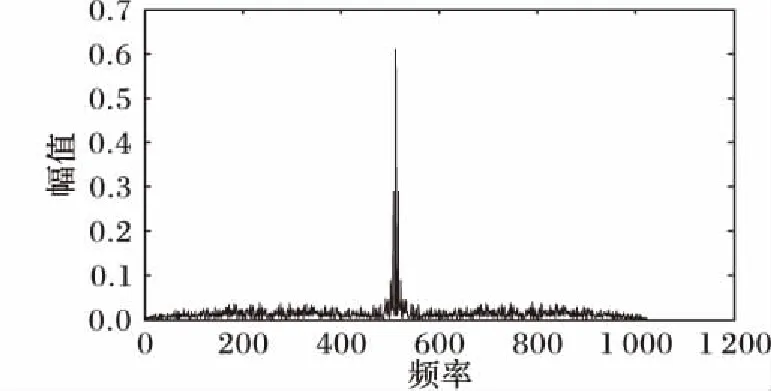
图15　收发端基函数互相关性能Fig. 15　Basic function correlation performance of transmitter and receiver

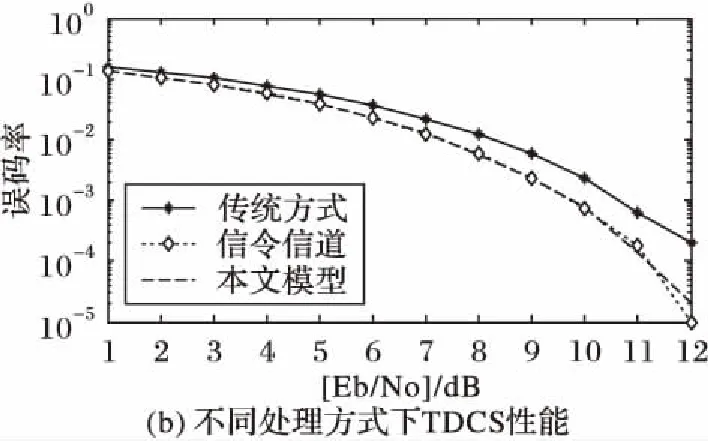
图16　不同处理方式下的TDCS性能Fig. 16　TDCS performance under different communication modes

参考文献:

[1]NI S P, DENG L H. Application on OFDM-based transform domain communication system in mine [J]. Applied Mechanics and Materials, 2012, 143-144: 843-848.

[2]王桂胜,任清华,刘洋,等.基于干扰模型的变换域优选算法研究[J].计算机仿真,2017, 34(4):66-71. (WANG G S, REN Q H, LIU Y, et al. The optimization of transform domain algorithm based on the jamming models [J].Computer Simulation, 2017, 34(4): 66-71.)

[3]HU S, GUAN Y L, BI G, et al. Cluster-based transform domain communication systems for high spectrum efficiency [J]. IET Communications, 2012, 6(16): 2734-2739.

[4]熊金石,任清华,李正刚.一种远距离航空型变换域通信系统设计与仿真[J].电讯技术,2009,49(2):14-18. (XIONG J S, REN Q H, LI Z G. Design and simulation of a long-distance aviation transform domain communication system [J]. Telecommunication Engineering, 2009, 49(2): 14-18.)

[5]谢铁成,达新宇,褚振勇,等.收发频谱不一致条件下的变换域通信系统基函数设计[J].吉林大学学报(工学版), 2014,44(6):1825-1830. (XIE T C, DA X Y, CHU Z Y, et al. Basis function design for transform domain communication system in the presence of spectral mismatches [J]. Journal of Jilin University (Engineering and Technology Edition), 2014, 44(6): 1825-1830.)

[6]王杰,毛玉泉,张衡阳,等.一种新的TDCS基函数生成方法及性能分析[J].空军工程大学学报(自然科学版),2014,15(2): 67-71. (WANG J, MAO Y Q, ZHANG H Y, et al. A new method of generating TDCS’s basis function and the analysis of its performance [J]. Journal of Air Force Engineering University (Natural Science Edition), 2014,15(2): 67-71.)

[7]刘立,张衡阳,毛玉泉,等.改进的TDCS基函数生成算法及性能分析[J].重庆邮电大学学报(自然科学版)，2016,28(3):312-318. (LIU L, ZHANG H Y, MAO Y Q, et al. Modified generation algorithm of basis function in TDCS and its performance analysis [J]. Journal of Chongqing University of Posts and Telecommunications (Natural Science Edition), 2016, 28(3): 312-318.)

[8]蒋莹,何明浩,郁春来,等.基于相位量化DRFM的欺骗干扰信号建模与分析[J].中国电子科学研究院学报, 2015(4): 361-366. (JIANG Y, HE M H, YU C L, et al. Modeling and analysis of deceptive jamming signal based on phase quantization DRFM [J]. Journal of China Academy of Electronics and Information Technology, 2015(4): 361-366.)

[9]ROMERO LAUROA L J, ROSANOVA M, MATTAVELLI G, et al. TDCS increases cortical excitability: direct evidence from TMS-EEG [J]. Cortex, 2014, 58: 99-111.

[10]O’SHEA J, BOUDRIAS M-H, STAGG C J, et al. Predicting behavioral response to TDCS in chronic motor stroke [J]. NeuroImage, 2014, 85(Pt 3): 924-933.

[11]LI Q, QU X, YIN L, et al. Generalized low-density parity-check coding scheme with partial-band jamming [J]. Tsinghua Science and Technology, 2014, 19(2): 203-210.

[12]SU Y, REN Q, MENG Q. A compressed sensing sparse channel estimation method for TDCS based on cyclic prefix [C]// ICSPCC 2015: Proceedings of the 2015 IEEE International Conference on Signal Processing, Communications and Computing. Piscataway, NJ: IEEE, 2015:1-5.

[13]QUAN Z, CUI S, SAYED A H, et al. Optimal multiband joint detection for spectrum sensing in cognitive radio networks [J]. IEEE Transactions on Signal Processing, 2009, 57(3): 1128-1140.

[14]谢铁城,达新宇,褚振勇,等.CCSK调制的变换域通信系统基函数序列估算方法[J].系统仿真学报,2014,26(8):1713-1717. (XIE T C, DA X Y, CHU Z Y, et al. Estimation of basis functions sequence for transform domain communication systems based on CCSK modulation [J]. Journal of System Simulation, 2014, 26(8): 1713-1717.)