基于动态近邻反馈修正的室内定位算法

党小超，黑毅力，郝占军，李芬芳

(1.西北师范大学 计算机科学与工程学院，兰州 730070；　2.甘肃省物联网工程研究中心，兰州 730070)(*通信作者电子邮箱hei_yili@163.com)

0　引言

无线传感器网络(Wireless Sensor Network， WSN)是一种低能耗、自组织、结构多样、连接广泛的网络系统，由大量无线传感器节点组成。其目的是实现节点间的合作，以感知、采集和处理覆盖区域中对象的信息，并最终发送给观察者。它在军事国防、工农业控制、城市管理、生物医疗、环境监测、目标跟踪、危险区域远程控制等应用中具备良好的应用前景[1]。在这些应用中，确定无线传感器节点的位置非常重要，定位技术也因此吸引了研究人员的广泛关注[2]。目前世界上使用的定位系统主要是全球定位系统(Global Positioning System, GPS)[3]，但是由于室内障碍物的存在，使得GPS信号很难被接收从而导致定位失效，所以人们通过WSN节点定位算法来寻求解决方案[4]。

在现有的无线传感器网络定位算法中，可以将定位算法分为基于距离的定位算法和距离无关的定位算法两大类[5]。前者需要测量待定位目标的距离或方位等位置参数以进行定位，主要测距技术有基于到达时间(Time Of Arrival, TOA)、基于到达时间差(Time Difference Of Arrival, TDOA)、基于到达角度(Angle Of Arrival, AOA)、基于接收信号强度(Received Signal Strength Indicator, RSSI)的定位等；在距离无关的定位算法中，如质心定位(Centroid)算法、距离向量-跳段定位(Distance Vector-Hop， DV-Hop)算法、自组织定位(Amorphous Positioning)算法、近似三角形内点测试法(Approximate Point-In-Triangle test， APIT)等，未知节点无须测量与邻居节点的距离或相对角度，而是利用连接或者跳数信息计算节点的位置。其中，RSSI测距技术因其成本低廉、能耗低等优势在无线定位技术中得到广泛应用。但在实际室内环境中，信号易受到室内地板、墙壁、人员走动等影响，产生多径效应，导致基于RSSI定位算法的定位精度下降。为了最大限度地消除RSSI测距误差对无线传感器节点自身定位精度的影响，文献[6]提出了一种基于RSSI的无线传感器网络距离差分修正定位算法(Distance Difference Localization Algorithm， DDLA)。该算法以三边定位算法为基础，将离目标节点最近的信标节点作为参考节点对基于RSSI的测距进行差分修正，最后利用差分和质心定位方法相结合的方式实现定位，在一定程度上减少了定位误差；但是该算法未能实现稀疏节点的定位，增加了网络中的通信开销。文献[7]为了解决传统的以蒙特卡罗为基础的移动定位算法中定位精度差、采样效率低的问题，提出了一种基于接收信号强度指示测距的蒙特卡罗盒定位(Monte Carlo Boxed localization， MCB)算法。该算法首先对RSSI的采样区域进行细化，以提高样本的成功率，最后利用估计节点运动轨迹的方法计算节点位置；然而该算法存在随机性较强、多次迭代耗时较长的缺陷。文献[8-9]考虑了三维空间中因接收信号的不确定性导致算法定位误差较大的因素，提出了混合测量定位算法。该算法将传统到达角度和接收信号强度的定位技术相结合，得到了混合测量的优化模型精确估计位置坐标，在一定程度上减少了定位误差和网络中的通信开销。文献[10]针对传统测距定位算法中无线信号传输模型及模型参数对环境因素依赖性强的特点，考虑传统的使用固定的路径损耗参数模型代替信号强度和距离的关系会造成较大误差，提出了一种新的动态估计路径损耗参数的方法。该算法首先确定最小定位子区域，然后利用已知参考节点的信息估计模型参数，最后实现准确测距，达到精确定位的目的。

通过对以上算法的研究及分析，提出了一种基于动态近邻反馈修正的室内定位算法FC-DNN(Feedback Correction of Dynamic Nearest Neighbors)。该算法为了减少环境因素带来的测距误差，在定位前首先通过区域划分思想确定最小定位区域，并在该子区域中利用节点间的几何关系估算路径损耗参数；同时引入向量混合积的概念对选取的信标节点进行过滤，使锚节点得到充分利用，同时降低定位算法对初始锚节点数量的需求；最后，动态选取锚节点并计算其定位误差因子来修正未知节点的坐标，进一步提高定位精度。

1　相关理论

1.1　基于信号衰减的距离估计模型及问题分析

目前，无线信号传输中最常用的是Shadowing模型[11]，即锚节点向未知节点广播信息，未知节点收到广播之后作出响应。当锚节点再次收到响应后，利用式(1)推算出与未知节点的距离。

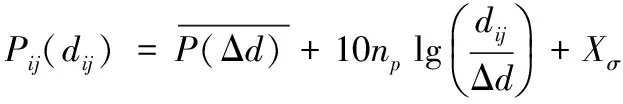
(1)

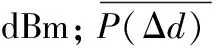
RRSSI=ARSSI-10nplg(d)

(2)

通过多次测量RSSI平均值后，利用式(2)可以计算出两点之间的距离RSSI。然而对数距离路径损耗模型方法存在两个主要缺点：一是RSSI值是高度随机的，并且易受多径和衰落的影响[13]；二是定位区域中路径损耗模型参数ARSSI和n与无线信号传输环境密切相关，且随着定位节点的移动参数也在不断变化中。为了解决这些问题，可以采用损耗参数动态估计的方式，即在定位区域选取两组已知锚节点，分别测出其距离及对应的RSSI值，并结合其已知的位置信息，借助式(2)计算定位区域中的路径损耗模型参数，减少测距误差，提高定位精度。

1.2　Voronoi图划分

Voronoi图又叫泰森多边形，作为计算几何中一种基本的几何结构，在解决无线传感器网络覆盖控制、网络定位等问题中应用广泛。它是由连接相邻两点的直线的垂直平分线组成的连续多边形组成。平面中的N个离散点按照最邻近原则把平面划分为几个区，该点所在的区是到该点距离最近点的集合。

假设P是由n个离散的传感器节点组成的集合，P={p1,p2,…pi…,pn}(2≤n<∞)平面上任意一点X(x,y)与节点pi(xi,yi)(pi∈P)的欧氏距离为：

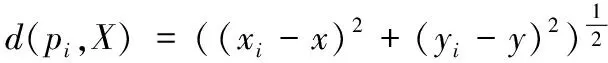
(3)

定义生长点pi的Voronoi多边形区域V(pi)为所有到pi距离最小点的集合：

V(pi,X)=

{x|d(pi,X)≤d(pj,X),∀i≠j,j=1,2,…,n}

(4)

整个平面被n个生长点划分为n个单元，而所有生长点pi的Voronoi多边形集合构成了P的Voronoi图，可以将其表示为V={V(p1),V(p2),…,V(pn)}。

1.3　Spearman等级相关系数

Spearman等级相关系数(Spearman’s rank correlation coefficientρ)是一种非线性相关测量方法，主要用于确定两组数据之间关联程度。假设给定两组不重复顺序样本数据{X1,X2,…,Xn}和{Y1,Y2,…,Yn}，定义xi(1≤i≤n)在{X1,X2,…,Xn}中的秩次为Ri，yi在{Y1,Y2,…,Yn}中的秩次为Qi，秩次差为di=Ri-Qi，利用式(5)计算相关系数为：

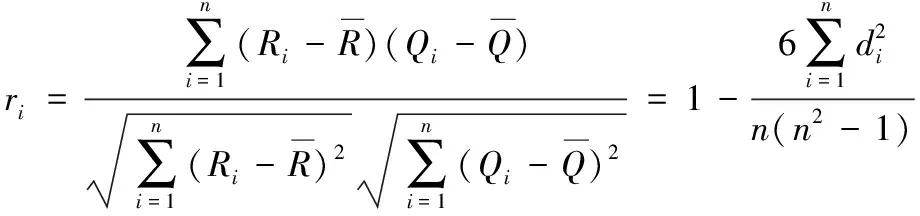
(5)

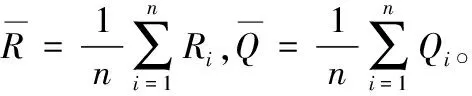
2　FC-DNN算法描述

动态近邻反馈修正的室内定位算法主要有三个阶段：1)区域划分判断阶段。使用Voronoi图对定位空间中信标节点进行区域划分，构造Voronoi多边形，判定待定位节点所在子区域。2)区域参数动态估计阶段。在室内狭小的范围内，通信信号在传输过程中受到的因素影响也相似，可以充分利用锚节点的位置信息动态估计子区域中的模型参数ARSSI、n。3)节点位置计算阶段。节点定位阶段分为节点预估计和节点反馈修正两个步骤，首先，利用已知信息及空间几何向量关系对节点定位，然后引入Spearman等级相关系数动态计算邻居锚节点反馈修正因子对初次定位结果进行修正。

2.1　区域划分判断阶段

为了使信号衰减的距离估计模型更加符合实际环境，同时考虑到室内复杂的环境因素对测距误差的影响程度，在实现无线定位之前，采用Voronoi图的构建思想将整体区域进行划分，目的是缩小被定位区域的范围，在分割后的子区域中拟合环境参数，从而进一步提高RSSI测量值的精确度和环境适应性。

如图1所示，假设实心五星节点代表锚节点Mi，空心圆代表未知节点U。随机选择k个锚作为初始节点，通过Voronoi图将区域划分，并且根据Voronoi图中任何多边形内的点到它所在区域的种子点的距离比到其他区域种子点的距离近的性质，可以计算出未知节点U与其他初始锚Mi之间的欧氏距离dui，选择距离最小的锚节点所在的区域即为待定位子区域。

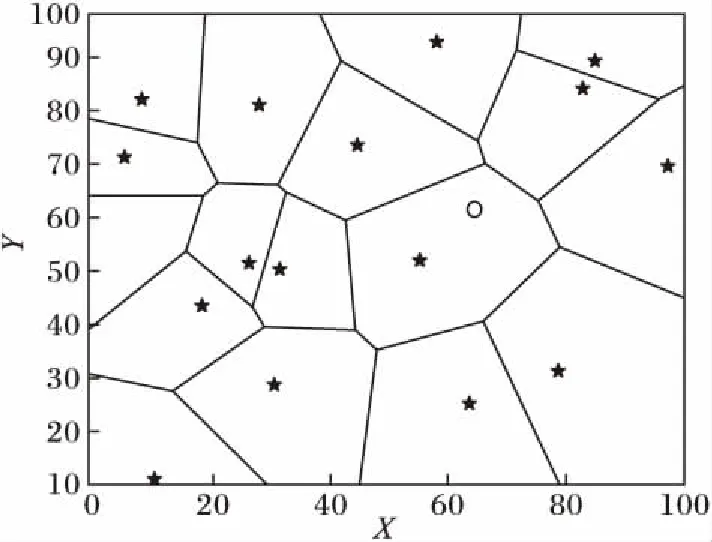
图1　Voronoi图的构建Fig. 1　Construction of Voronoi diagram

2.2　定位区域路径损耗参数动态估计阶段

由于基于RSSI测距模型参数ARSSI、n在实际环境中会随着诸多因素的改变而不同，所以本文利用一种动态估计路径损耗模型参数的方法[14]，以减小测距模型的误差,从而提高定位精度。因为算法在第一阶段对定位区域进行了有效的划分，在一个非常小的范围内，物理位置越接近，信号的通信环境也越相似，可以认为在定位子区域中的路径损耗模型也近似相同。假设节点之间可以相互通信，可以充分利用锚节点的位置信息估计定位区域内路径损耗参数。

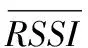
根据式(2)可以建立方程组：

(6)

(7)

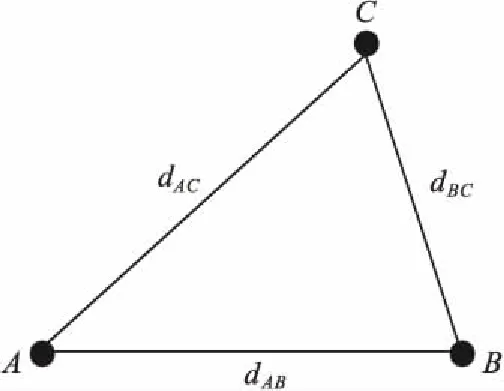
图2　区域内路径损耗模型参数计算Fig. 2　Parameters calculation of path loss model in each region

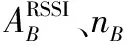
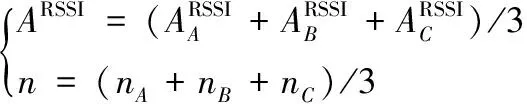
(8)

2.3　节点位置计算阶段

假设在三维空间中分布着N个位置已知的锚节点Mi(i=1,2,…,N)，其位置坐标为(Mix,Miy,Miz),同时区域中未知节点U的位置坐标表示为(Ux,Uy,Uz)，未知节点U与锚节点Mi间的RSSI测量值表示为RSSi。节点位置计算阶段具体步骤如下：

步骤1节点共线过滤。在确定未知节点定位区域后，选取最优RSSi，即未知节点在收到超过阈值m(文中m=4)个信标信息后，至少需要4个锚节点作为参考节点进行自身定位计算，其中三个锚节点用于初步几何向量定位，其余锚节点将充当修正节点对初步定位坐标进行修正。因此至少获取4点位置信息用以定位未知节点，但是存在两种特殊情况无法完成定位，即当获取的4点在同一个平面上或者其中存在3点在同一条直线上。为了解决这个问题，本文根据空间向量理论来过滤这些节点。假设对于获取的4个锚节点M1、M2、M3和M4，利用式(9)的进行检验，如果存在向量M1M2，M1M3和M1M4的混合积不为0，则利用这4个不共面的点的坐标来计算待定位节点的坐标位置[15]。否则，返回继续寻求符合条件的锚节点。

[M1M2,M1M3,M1M4]=(M1M2×M1M3)×M1M4=

(9)

通过上面的过滤处理，可以得到4个有效的锚节点来计算未知节点的位置。

然后利用已知信息及空间几何关系对未知节点定位。

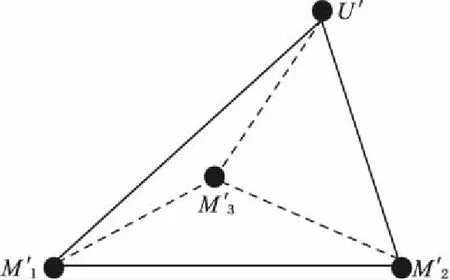
图3　锚节点反馈的几何定位Fig. 3　Geometric localization of anchor node feedback

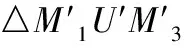
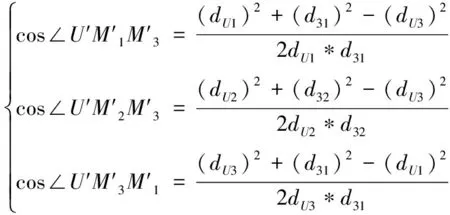
(10)

又根据向量的定义可得：

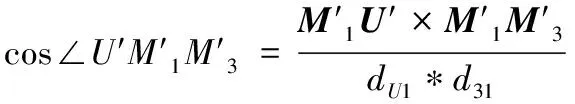
(11)

所以联合方程(10)和(11)建立方程:

(12)

同理可得：

(13)

(14)

通过式(12)、(13)、(14)得到的就是待定位节点U′的初步定位坐标，因为对节点进行了筛选过滤，同时几何向量的算法也很好地消除了多解问题。

步骤3锚节点反馈修正。利用步骤1中节点过滤方法和Spearman等级相关系数动态判断选定锚节点的邻居节点及个数，根据最近锚节点通过对比其定位结果与自身实际位置得到修正因子，并将值反馈给邻居未知节点,邻居未知节点利用收到的修正因子对最终定位结果进行修正，得到更加精确的定位坐标。

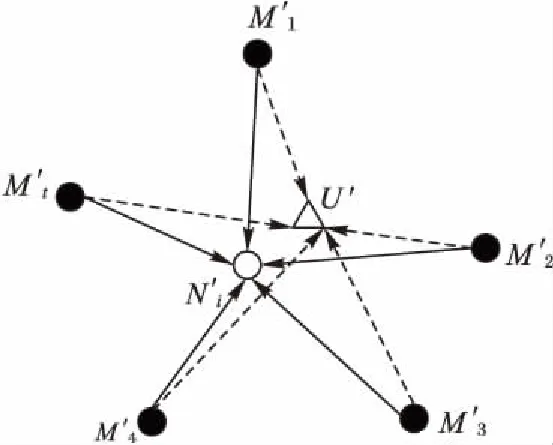
图4　邻居节点示意图Fig. 4　Illustration of neighbor nodes

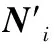
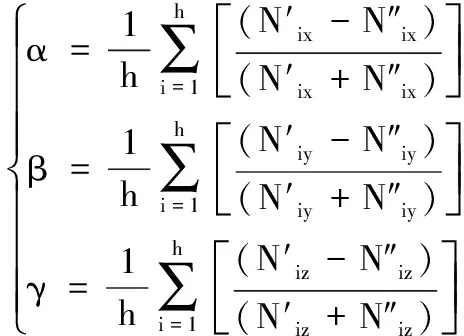
(15)

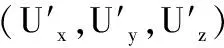
(16)

3　实验仿真与分析

为了检验FC-DNN算法的性能，使用Matlab 2016仿真实验平台进行仿真实验,并与基于RSSI的无线传感器网络距离差分修正定位算法(DDLA)[6]、受限三维空间传感器定位(CO-3D)算法[16]在误差、能耗方面进行比较。详细仿真参数信息如表1所示。

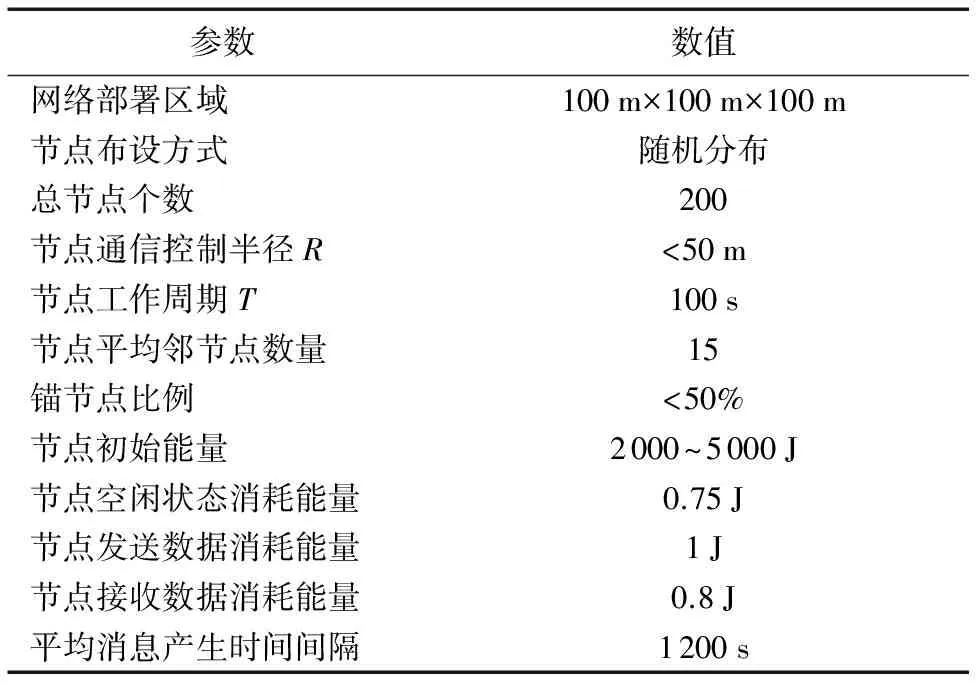
表1　仿真参数Tab. 1　Parameters of simulation

3.1　定位误差率比较

为了刻画FC-DNN算法的性能，减少实验中随机误差的干扰，最终结果取30次实验的平均值。采用均一化定位误差来评价算法性能，均一化定位误差定义为：

error=

(17)

式中:(xi,yi,zi)为未知节点i的实际坐标，(xki′,yki′,zki′)为第k次估计的未知节点i的坐标，N为未知节点数量，R为通信半径，K为实验次数。

图5显示了在固定节点通信半径而锚节点个数变化时，FC-DNN算法与其他两种算法的均一化定位误差比较。从图5可以看到，随着锚节点个数的增加，定位误差总体呈下降趋势，这是因为在定位前期过程中随着更多有效锚节点被引入参数和坐标计算，在一定程度上提高了定位精度。根据仿真结果的统计数据，本文算法的平均定位精度约为33%，而CO-3D、DDLA算法平均定位精度分别为48%和46%，综合分析，在不同的锚节点个数时，FC-DNN算法的误差相比其他两种算法都更低。尤其在锚节点个数超过50%时，其误差下降速度加快。这是因为FC-DNN算法是对若干个可能的节点位置利用邻居节点进行修正计算，同时算法通过增加对锚节点的判断、过滤操作得到了符合条件的锚节点信息，而两种对比算法仅利用求平均值的方法得到最终坐标，误差较大，相比之下，FC-DNN算法的定位精度更高。

图6为定位过程中随着节点通信半径R的增大，不同锚节点个数时，FC-DNN算法与CO-3D和DDLA算法的均一化定位误差比较。从图6可以看出，当锚节点比例确定时，随着R增大，节点定位误差均呈下降趋势，这是因为随着通信半径增大，节点覆盖区域呈正相关，即提高了网络连通性，定位更加准确。仿真结果显示在相同条件下，FC-DNN算法相比CO-3D算法和DDLA算法的误差始终最低，而且更加平缓，尤其是与CO-3D算法相比，因为锚节点的信息得到更加充分的利用，多次累计定位减少了定位误差率(约15个百分点)，提高了节点的定位精度，说明本文的算法对通信半径的改变并不敏感，更加稳定。

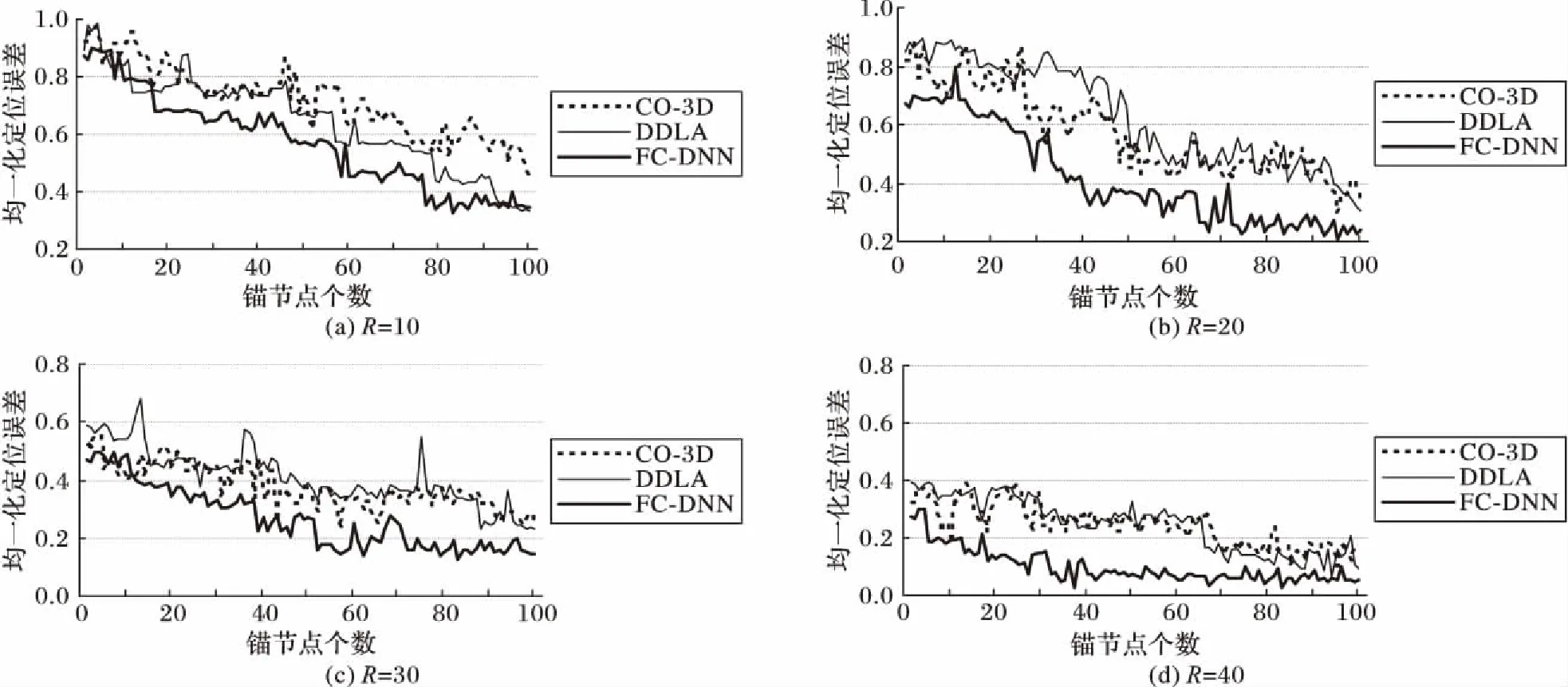
图5　均一化误差随锚节点个数的变化Fig. 5　Normalized position error with different number of anchors nodes

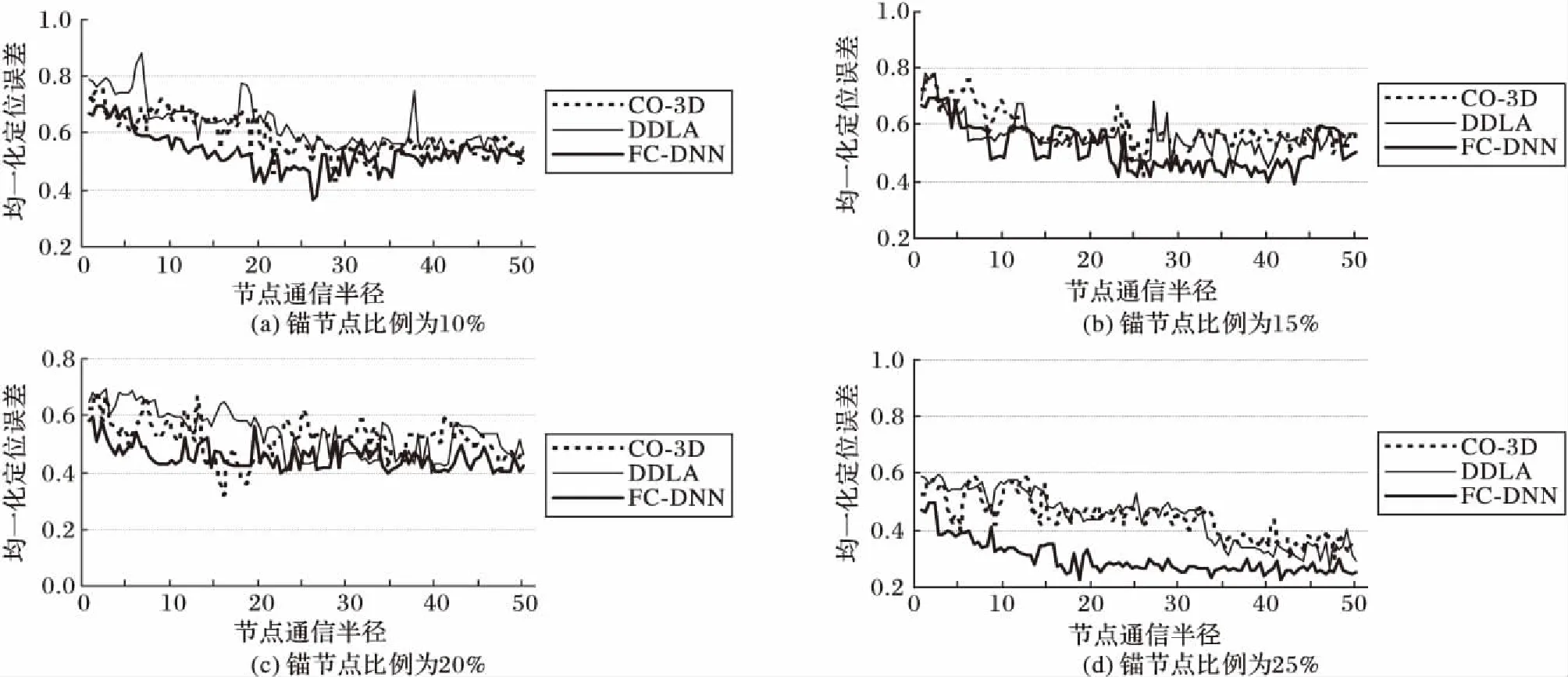
图6　均一化误差随节点通信半径的变化Fig. 6　Normalized position error with different node communication radius

3.2　能耗比较

设置固定的节点通信半径，当锚节点数取不同值时，FC-DNN算法与CO-3D算法和DDLA算法的能耗比较如图7所示。图7显示的能耗与实际情况吻合，原因是在FC-DNN算法中，首先对区域进行了合理的划分，在待定位区域内，通过筛选最优邻居节点实现定位。FC-DNN算法由于对区域进行合理划分后，将空间复杂度降为O(lbn)，而CO-3D算法的空间复杂度为O(n)，同时其不断随机选择几个可能的锚节点进行定位也导致了定位能量的消耗。而且本文算法通过过滤优选邻居锚节点，使得在每轮计算中锚节点信息得到充分利用，使用频率大幅度降低，同时延长了整个系统的生命周期，提高了定位的覆盖率和成功率，所以FC-DNN算法的能耗最低。

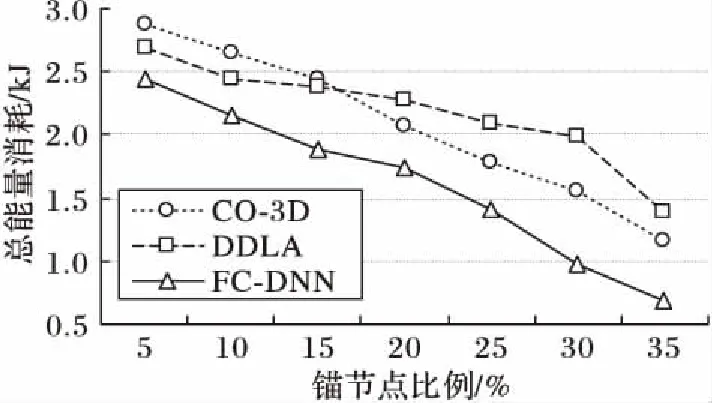
图7　能耗随锚节点个数的变化Fig. 7　Energy consumption with different number of anchor nodes

4　结语

针对无线传感器网络中基于RSSI测距模型中可能由于反射、多径效应和天线增益导致重大的传播损耗而引起定位精度的问题，提出了动态邻居锚节点反馈修正算法，引入锚节点反馈修正因子来修正未知节点的坐标，有效解决了传统的RSSI测距技术导致定位结果误差比较大的问题。通过仿真和实验结果验证，与CO-3D算法和DDLA算法相比，该算法在定位误差、平均能耗等方面性能更优，能够更精确地定位节点。但是，当划分后的定位区域中锚点数比较稀疏时，定位仍存在困难，同时区域划分判断阶段也以消耗定位时间为代价，这是以后研究需要解决的问题。

参考文献:

[1]ZHANG R, XIA W, JIA Z, et al. The indoor localization method based on the integration of RSSI and inertial sensor [C]// GCCE 2014: Proceedings of the 2014 IEEE 3rd Global Conference on Consumer Electronics. Piscataway, NJ: IEEE, 2014: 332-336.

[2]ADEWUMI O G, DJOUANI K, KURIEN A M. RSSI based indoor and outdoor distance estimation for localization in WSN [C]// ICIT 2013: Proceedings of the 2013 IEEE International Conference on Industrial Technology. Piscataway, NJ: IEEE, 2013: 1534-1539.

[3]MEHRA R, SINGH A. Real time RSSI error reduction in distance estimation using RLS algorithm [C]// IACC 2013: Proceedings of the 2013 IEEE 3rd International Advance Computing Conference. Piscataway, NJ: IEEE, 2013: 661-665.

[4]YASSIN A, NASSER Y, AWAD M, et al. Recent advances in indoor localization: a survey on theoretical approaches and applications [J]. IEEE Communications Surveys & Tutorials, 2017, 19(2): 1327-1346.

[5]钱志鸿，孙大洋，LEUNG Victor.无线网络定位综述[J].计算机学报，2016，39(6):1237-1256. (QIAN Z H, SUN D Y, LEUNG Victor. A survey on localization model in wireless networks [J]. Chinese Journal of Computers, 2016, 39(6): 1237-1256.)

[6]任维政，徐连明，邓中亮，等.基于RSSI的测距差分修正定位算法[J].传感技术学报，2008，21(7):1247-1250. (REN W Z, XU L M, DENG Z L, et al. Distance difference localization algorithm based on RSSI for wireless sensor networks [J]. Chinese Journal of Sensors and Actuators, 2008, 21(7): 1247-1250.)

[7]武晓琳，单志龙，曹树林，等.基于接收信号强度指示测距的蒙特卡罗盒移动节点定位算法[J].计算机应用，2015，35(4):916-920. (WU X L, SHAN Z L, CAO S L, et al. Monte Carlo boxed localization algorithm for mobile nodes based on received signal strength indication ranging [J]. Journal of Computer Applications, 2015, 35(4): 916-920.)

[8]SINGH A, KUMAR S, KAIWARTYA O. A hybrid localization algorithm for wireless sensor networks [J]. Wireless Personal Communications, 2013, 71(2): 1365-1385.

[9]严长虹，马静.三维传感网空间RSS与AOA混合测量的精确定位方法[J].传感技术学报，2017，30(3):450-455. (YAN C H, MA J. Precise positioning method with hybrid RSS and AOA measurement in 3-D WSN space[J]. Chinese Journal of Sensors and Actuators, 2017, 30(3): 450-455.)

[10]李瑶怡，赫晓星，刘守印.基于路径损耗模型参数实时估计的无线定位方法[J].传感技术学报，2010，23(9):1328-1333. (LI Y Y, HE X X, LIU S Y. Wireless localization algorithm based on path loss model parameter estimated in real time[J]. Chinese Journal of Sensors and Actuators, 2010, 23(9): 1328-1333.)

[11]AWARD A, FRUNZKE T, DRESSLER F. Adaptive distance estimation and localization in WSNs using RSSI measures [C]// DSD 2007: Proceedings of the 2007 IEEE 10th Euromicro Conference on Digital System Design Architectures, Methods and Tools. Piscataway, NJ: IEEE, 2007: 471-478.

[12]胡咏梅，张欢.一种改进的无线传感器网络质心定位算法[J].计算机工程与科学，2012，34(2):45-49. (HU Y M, ZHANG H. An improved algorithm for the centroid localization of wireless sensor network [J].Computer Engineering and Science, 2012， 34(2): 45-49.)

[13]XUE W, QIU W, HUA X, et al. Improved Wi-Fi RSSI measurement for indoor localization [J]. IEEE Sensors Journal, 2017, 17(7): 2224-2230.

[14]ZHENG J, WU C, CHU H, et al. An improved RSSI measurement in wireless sensor networks [J]. Procedia Engineering, 2011, 15: 876-880.

[15]戴桂兰，赵冲冲，邱岩.一种基于球面坐标的无线传感器网络三维定位机制[J].电子学报，2008，36(7): 1297-1303. (DAI G L, ZHAO C C, QIU Y. A localization scheme based on sphere for wireless sensor network in 3D [J]. ACTA Electronica Sinica, 2008, 36(7): 1297-1303.)

[16]LIANG J, SHAO J, XU Y, et al. Sensor network localization in constrained 3-D spaces [C]// Proceedings of the 2006 IEEE International Conference on Mechatronics and Automation. Piscataway, NJ: IEEE, 2006: 49-54.