一种堆垛机状态异常区间自动筛选新方法

赵良德, 梁胜涛, 陈良坤, 张宏生, 杨　乐, 梁晓伟, 黄大荣

(1.国网安徽省电力有限公司电力科学研究院, 安徽 合肥　230000;2.重庆交通大学, 重庆　400074)

随着经济的快速发展,立体仓库越来越趋向于自动化、智能化。自动化智能仓储系统具有空间利用率高、便于实现自动化管理、实时自动结算库存货物种类和数量、立体仓库信息库可以和中央计算机系统联网运行等许多优点,对加快物流速度、提高劳动生产率、降低生产成本都有重要意义,已开始应用于汽车、电子、医药、烟草、建材、邮电等许多行业。堆垛机是自动化立体仓库中最主要的作业机械设备,是输送系统的核心设备,是决定整个出入库是否能流畅运行的关键。故检测其状态异常点并及时维修是保证堆垛机的安全正常运行的有效手段,从而保障智能运维仓库正常运行。基于此,如何有效地检测堆垛机状态异常区间逐渐成为学者研究的重点[1-2]。但遗憾的是国内目前对堆垛机的研究大多数是从结构设计或者控制角度进行的研究,而基于堆垛机运行状态数据进行分析的还没有。

为解决上述问题,本文提出一种基于堆垛机运行状态数据异常检测方法。首先,建立均值平滑模型,对数据进行预处理;其次,利用箱形图法建立异常区间筛选模型,对异常区间进行定位。最后,利用从电力行业自动化智能仓储系统中采集的堆垛机运行信号进行实例验证,证明算法的工程有效性和适用性。

1　数据均值平滑处理

1.1　数据分析

分析现今所采集得到的数据包括3-6月堆垛机的电流及振动数据,其采集位置范围为:0m-24m。数据分布如图1所示。

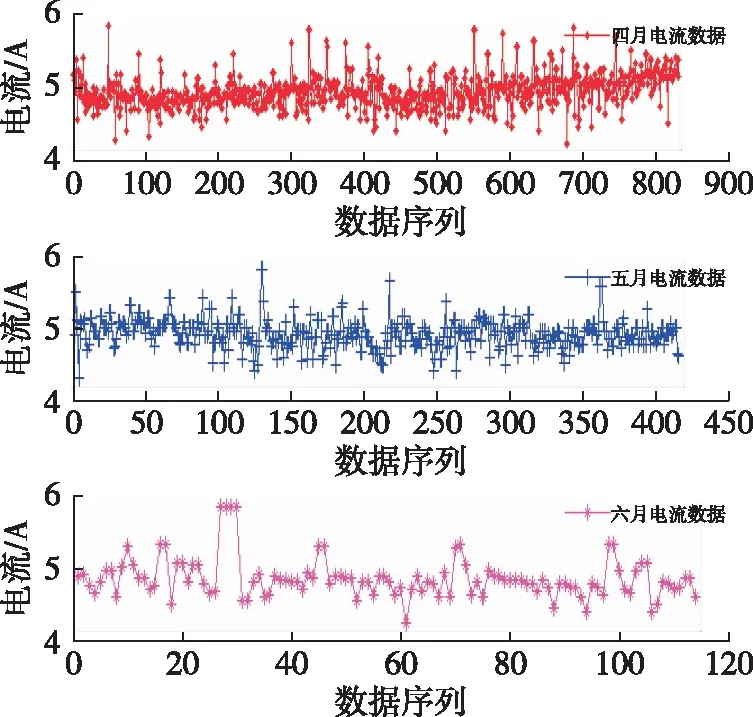
图1　原始电流数据

由图1可知,原始数据杂乱无序,样本量过大。从原图上无法发现任何规律及有用信息,因此对首先得数据进行均值平滑处理,既可减少数据量大小,又可增强其规律性。

1.2　数据平滑处理

实际运行过程中,存在运行区间重复,含有启动电流与停止电流;偶发性故障与隐形故障存在相互干扰,区间均值对数据进行平滑。为此,本文建立一种数据平滑模型,总体分为两步:区间采样[3-5]和均值平滑。

1)区间采样

为解决采样数据区间重复问题,将堆垛机运动数据采集等区间划分,设置区间采样参数如下:

区间采样起点:start=0 mm；

区间采样间隔:interval=100 mm。

综上可知,均值平滑即将0m-24m划分如下:[0 100]、[101 200]…直到取到24m。

2) 均值平滑

对于给定区间I,在这个区间所包含信号集表示为SI(t)=(s1(t),s2(t),…sN(t)),规定这个区间值为

(1)

由此可知,平滑后的区间信号集如下:

S=(S1′,S2′…SM′)

(2)

其中,M=24000/100=240。

数据平滑整体算法流程如图2所示。

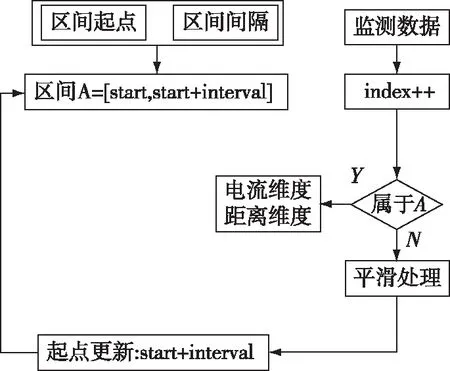
图2　平滑算法流程

利用Matlab软件对上述进行实现,堆垛机运动状态数据平滑结果如图3所示。

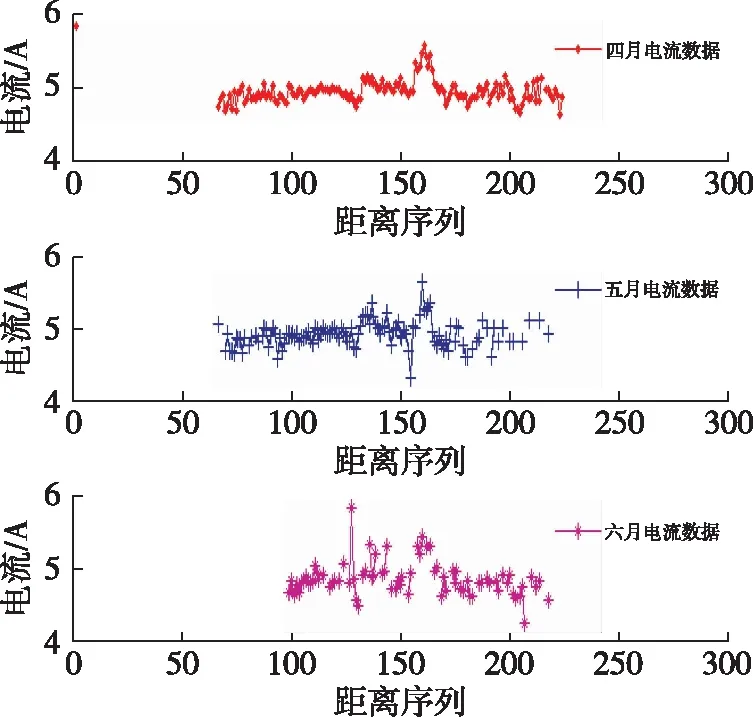
图3　4-6月份电流平滑结果

1.3　机动目标跟踪技术的发展

对比分析原始信号和均值平滑后信号,可发现,均值平滑后的信号规律性更强,更清晰。总之,均值平滑后的信号更利于异常区间的定位及筛选。

2　基于箱形图法的异常区间定位

箱线图需要用到统计学的四分位数(Quartile)的概念,所谓四分位数,就是把组中所有数据由小到大排列并分成四等份,处于三个分割点位置的数字就是四分位数[6-8]。

由于堆垛机运行状态数据属于无标签数据,因此在进行异常检测时只能设定异常数据占总体百分比。而箱形图法可以自主设定其百分比,自动筛选异常点。

异常值通常定义为小于QL-1.5IQR或大于QL-1.5IQR的值。其中,QL称为下四分位数,表示全部观察值中有四分之一的数据取值比它小;QU称为上四分位数,表示全部观察值中有四分之一的数据取值比它。IQR称为四分位数间距,QU是上四分位数与下四分位数QL之差,其间包含了全部观察值的一半。如图4所示。

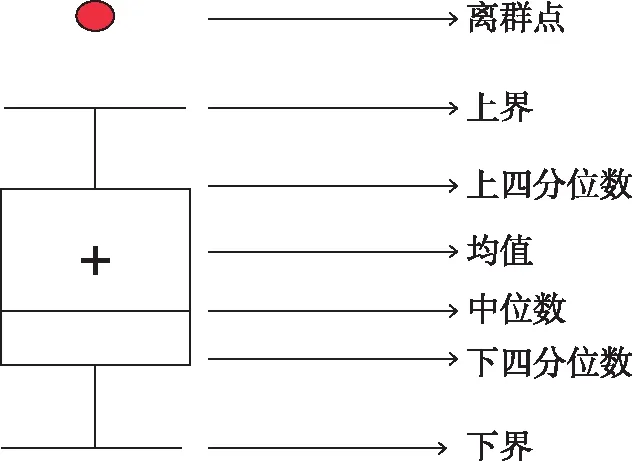
图4　箱形图算法原理

3　实验验证

自动化立体仓库(ASRS)作为现代物流的核心技术之一,受到了各类企业的普遍关注,广泛应用于各个领域中。其中堆垛机作为自动化立体仓储系统中的最关键设备,随着运行速度不断提高,而随之带来堆垛机异常问题越来越多。因而,检测堆垛机的运行状态异常是整个自动化物流系统的异常检测关键。本文以电力行业自动化智能仓储系统中的堆垛机电流信号为数据源,其中数据中包含了轨道焊缝、轨道凹凸等异常。如图5-7所示。

图5　位置大约为7200mm天轨接头处

图6　位置大约为13000mm地轨凹陷

图7　位置大约为15200mm地轨凹陷

此外,在轨道20m,10m,18m分别都有轨道焊缝。

首先利用等区间采样定理进行区间采样,其次利用均值对采样数据进行平滑处理,最后利用箱形图法对平滑处理后数据进行异常点筛选。如果只进行异常点筛选会造成误判结果太大,且由于采集信号时存在时延,因此导致记录位置存在误差。为此,对所检测出的异常点进行区间拓展,仿真结果如图8(a-c)所示。

图8(a)　4月份电流数据箱线图结果

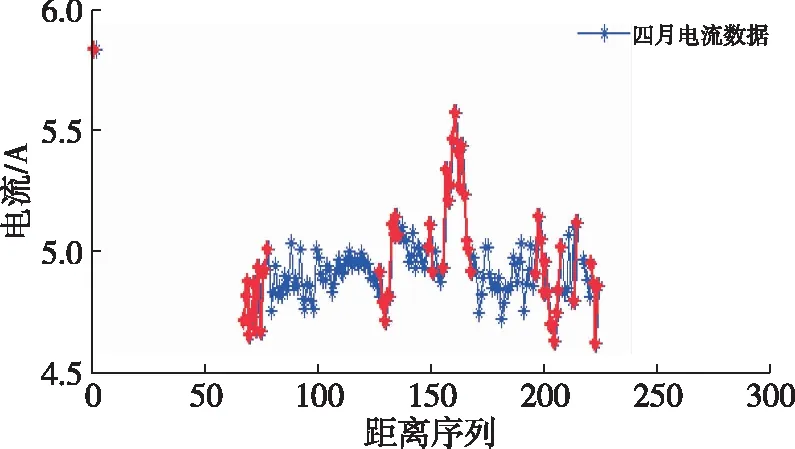
图8(b)　4月份电流数据异常点检测结果

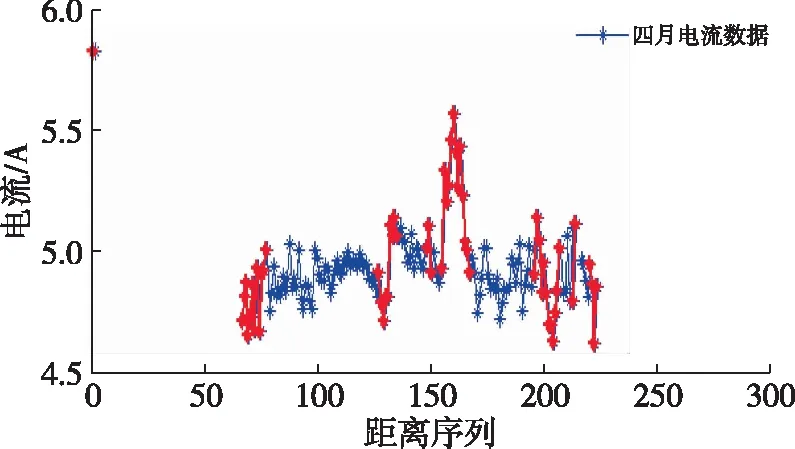
图8(c)　4月份电流数据异常区间检测结果

仿真检测异常区间如表1所示。

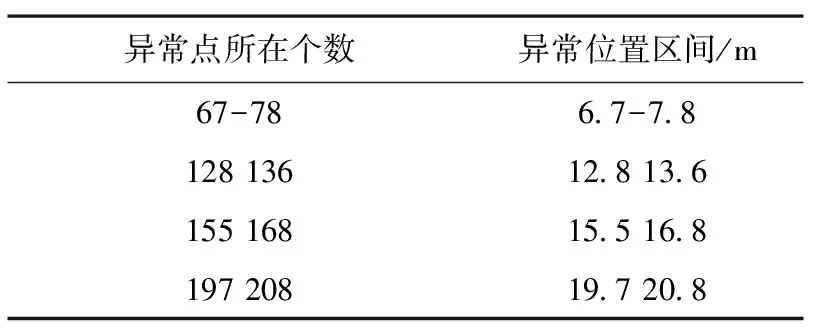
表1　4月份异常位置区间

利用5月份电流数据进行仿真,结果如图9(a-c)所示。

图9(a)　5月份电流数据箱线图结果

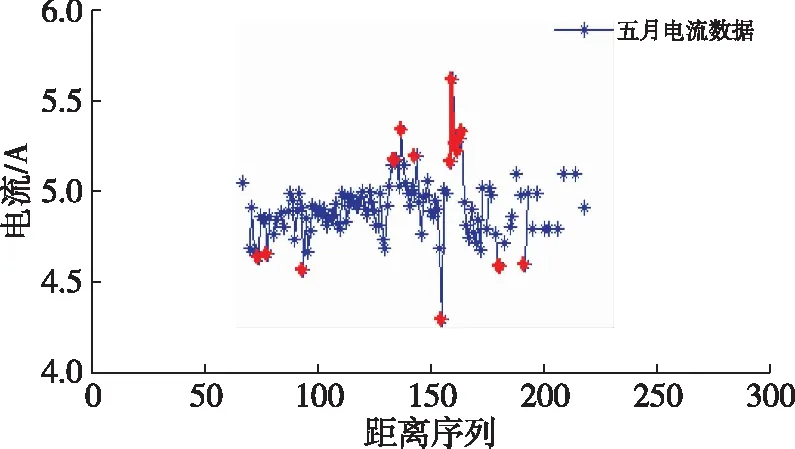
图9(b)　5月份电流数据异常点检测结果

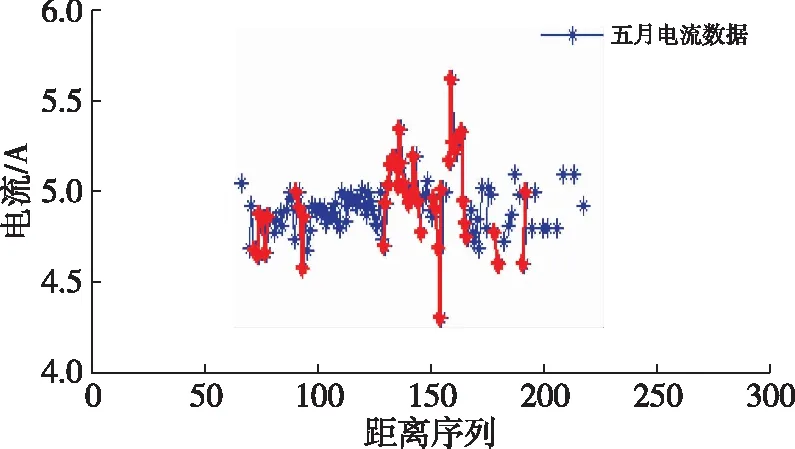
图9(c)　5月份电流数据异常区间检测结果

从图9可知,由5月份堆垛机电流数据所得的异常区间如表2所示。

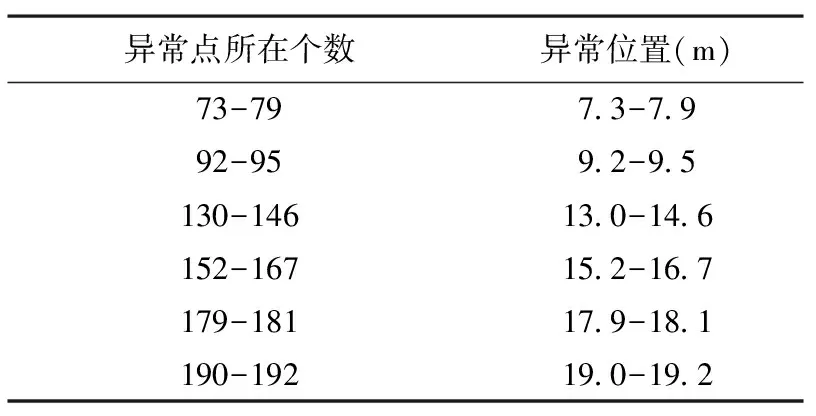
表2　5月份异常位置区间

利用6月份电流数据进行仿真,结果如图10(a-c)所示。

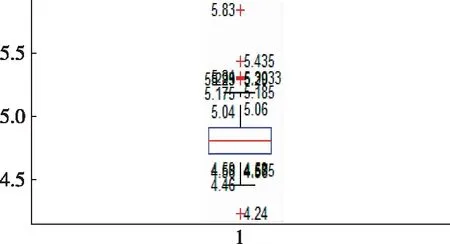
图10(a)　6月份电流数据箱线图结果

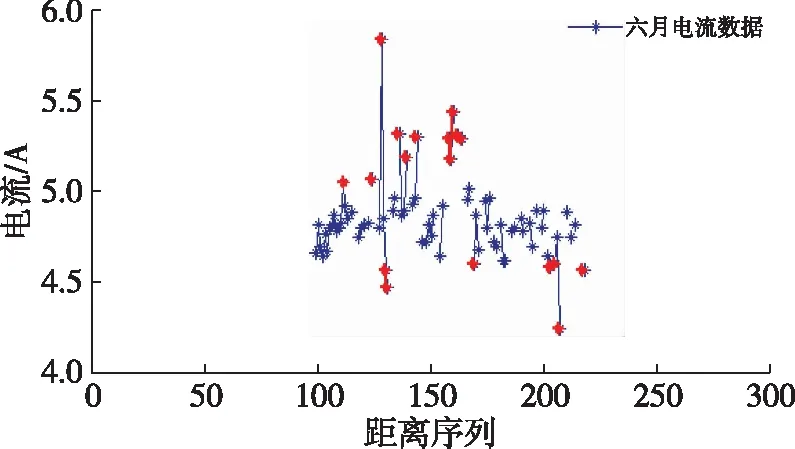
图10(b)　6月份电流数据异常点检测结果

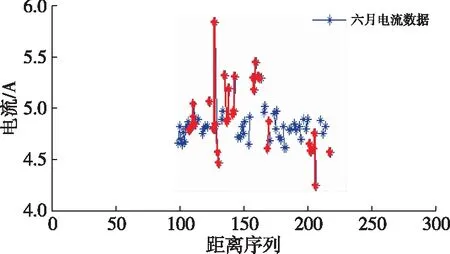
图10(c)　6月份电流数据异常区间检测结果

从图10可知,由6月份堆垛机电流数据所得的异常区间如表3所示。

表3　6月份异常位置区间

4　结束语

本文首先通过将堆垛机运行轨道进行区间划分,并利用等区间采样对原始数据进行采样,其次利用均值平滑对每个区间进行均值处理。对比均值平滑后的信号图和原始信号图,发现均值平滑后的信号图数据量更少,规律性更强。再者,利用箱形图法对平滑后的信号进行异常点筛选,筛选结果与堆垛机轨道现场异常相吻合,证明了本文所提出的异常检测方法的有效性和工程可靠性。

参考文献:

[1]吕婷,杨涛,韩宾,等.基于模糊贝叶斯网络的堆垛机系统可靠性分析[J].计算机应用研究,2014,31(12):3632-3636.

[2]范红岩,刘军,张可薇.堆垛机状态监测与故障诊断的研究和进展[J].物流技术,2017,36(2):33-37.

[3]贾继德,陈荣刚,陈剑.基于抽区间采样的内燃机状态监测方法研究[J].内燃机工程,2005,26(6):72-75.

[4]宋晓宇,郭寒冰,袁帅,等.基于自适应阈值区间的动态采样Hough变换直线检测算法[J].沈阳建筑大学学报(自然科学版),2014,30(5):945-952.

[5]周彪,李乔,周筱航.基于探索性数据分析的桥梁模态识别数据处理方法[J].四川建筑科学研究,2017,43(2):33-37.

[6]李新春,侯跃.基于改进AP选择和K最近邻法算法的室内定位技术[J].计算机应用,2017,37(11):3276-3280+3287.

[7]李梦辉,桑小田,田振川,等.箱形图在长江流域棉区棉花含杂率异常值检验中的应用[J].湖北农业科学,2016,55(11):2895-2898+2954.

[8]赵超.偏态抗差箱形图函数分析[J].武汉大学学报(工学版),2015,48(6):778-781.