基于变步长稀疏A*搜索和MPC的多无人机层次化协同航迹规划*
薄 宁, 李相民, 代进进, 唐嘉钰
(海军航空大学, 山东 烟台 264001)
无人机(Unmanned Aerial Vehicle, UAV)由于其独有的成本、机动性等优势,目前已被广泛用于战术压制敌防空系统、侦察搜索、定位跟踪、战毁评估等枯燥、危险、恶劣的战术任务[1]。灵活高效的自主航迹规划是无人机系统生存与成功的核心基础之一[2],其成为近年来理论研究的重难点问题之一。
UAV航迹规划可分为路径规划和轨迹规划。路径规划结果是与时间无关的静态几何路径。轨迹规划比路径规划更为细化,规划结果是与时间相关的三维空间曲线。路径规划主要求解方法分为两类:一类是确定型搜索算法,如D*算法、A*算法、Dijkstra算法[3]等;一类是随机型搜索,如遗传算法、粒子群算法等。但路径规划方法一般不考虑UAV动力学与运动学约束,结果较为粗略。轨迹规划方法分为直接法与间接法两种,直接法又可分为可行方向法、非线性规划法等;间接法如牛顿法,最速下降法、共轭梯度法等[4]。轨迹规划方法可以求得UAV运动控制的较优解,但随着避障、避碰、多机协同等约束的增多以及规划地域范围的扩大,其求解复杂度增大,实时性降低。例如,文献[5]考虑UAV动力学运动学约束、避障约束,建立了UCAV武器投放轨迹规划最优控制问题框架,使用Gauss伪谱法求解,仿真结果表明,在使用较少插值点的情况下,计算时长仍在十几秒左右。
针对上述问题,本文提出了一种路径规划与轨迹规划相结合的多UAV实时航迹规划层次结构策略。在路径规划阶段,考虑避障等约束,建立了路径规划问题模型,针对传统稀疏A*算法中步长固定的限制,提出了一种连续可变步长的SAS算法,对问题进行了求解,得到由中间航路点连接而成的多条航路段;然后,针对任一中间航路段实时轨迹规划过程,设计了基于DMPC思想的轨迹规划问题求解框架,综合考虑UAV运动学约束、避碰约束,建立了DMPC单步非线性规划模型。仿真结果表明,该策略求解速度快,所得解较优,能够满足UAV在线实时航迹规划需求。
1 问题分析与求解框架
由于UAV可以应用于多种不同的战场环境和战术用途,在进行航迹规划时,需要考虑的因素条件,例如优化目标、约束条件、协同要求、时限要求等各不相同,首先对所研究的问题背景进行分析和描述,然后选择优化问题所建立的模型和求解方法,并确定问题的整体求解框架。
1.1 问题分析
本文研究的问题背景是多UAV协同执行任务中的航迹规划问题。每架UAV上除挂载任务载荷外,还具有一定范围内的数据通信机制以进行相邻UAV间的状态信息通报。本文研究的内容为:UAV在分别接收所分配的任务后,从当前时刻点到任务点航线飞行中考虑避障、避碰、到达时间等多种约束的航迹规划问题。航迹规划考虑主要因素有:1)障碍物规避约束,如山川地形障碍、气象禁飞区、敌方雷达等;2)任务执行过程中的突发威胁,包括实现通过侦查情报已经获知的敌方预警雷达、防空系统,以及在执行任务过程中侦察发现或者接收的敌方威胁;3)己方UAV间的避碰以及UAV与有人机间的避碰问题;4)计算实时性要求。
1.2 求解框架
根据对于UAV编队协同作战航迹规划问题的分析,本文设计了UAV层次化航迹规划结构,每架UAV上运行的航迹规划框架如图1所示。

图1 层次化航迹规划结构
方案采用完全分布式求解策略,每架UAV无须存储全局战场态势,而是仅存储任务执行区域相关的战场态势信息。每架UAV接收任务,负责为自身平台进行航迹规划。多UAV间的时间协同关系由任务管理单元进行规划前解耦。第一步为路径规划过程,此阶段根据指控节点提供的分配任务以及本机状态,态势管理单元提供的各类障碍物,协同UAV任务完成情况等各种信息,将其转换为路径规划问题模型,并使用连续可变步SAS算法进行求解,将生成的由多个中间航路点组成的航路规划结果交至第二阶段的航线存储单元。同时,路径规划过程根据一定的触发条件(例如任务改变、新的威胁区出现等)进行航迹重规划判断,若满足条件,则进行航迹在线规划以满足态势变化。经过第一阶段处理后,整个航迹被分解为多段小的航路段,再在每一航路段上运行第二阶段的轨迹规划过程。
第二个过程为轨迹规划过程,轨迹规划过程基于模型预测控制(Model Predictive Control, MPC)思想,在每个时域周期内,根据预先建立的UAV运动预测模型,推导出预测域内的UAV多步状态,然后通过避碰管理单元输出的本时刻避碰约束,采用轨迹规划中的直接法,建立非线性规划问题模型并进行求解,所得解为多步控制向量序列,取出第一个向量交由UAV控制器进行执行。整个流程在一个步长周期内运行一次,不断循环,从而构成一个滚动在线规划过程。
2 路径规划过程
路径规划过程部分综合考虑地形、禁飞区、敌方威胁等情况,为UAV生成一条可飞航路并根据环境变化进行重规划。本文不考虑UAV的飞行高度变化,假设所有UAV均在同一高度平面内飞行。
2.1 环境建模
首先在UAV任务空间建立直角坐标系,并对整个任务区域的战场环境进行建模,将整个战场划分为若干正方形栅格,栅格的边长依据式(1)确定[6]。
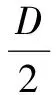
(1)
其中,D为网格边长,δN为UAV导航系统误差,δM为数字地图误差,δA为其他误差。K为兼顾鲁棒性和算法运算速度的系数。
文献[6]提供了航路规划时,地形高程、威胁危险、战略回避三种威胁区的单元格代价计算方法,本文为简化计算,将地形障碍、禁飞区、威胁区等统一处理为禁飞区,规划航路不得穿越标识为禁飞区的单元格,定义单元格代价为
(2)
其中,(xi,yj)为单元格坐标,C(xi,yj)为单元格(xi,yj)的代价值。
2.2 问题建模
航路规划的一般问题模型为寻找一条从起始点到终点的航路,使得经过航路的代价最小。由于本文中将安全区单元格代价定义1,威胁区单元格代价定义为无穷大,则航路总代价最小等效为航路路径在满足避障的条件下路径总长度最小,则问题可描述为

(3)
其中,Np为UAV规划的航路点数量,Lineseg(j+1,j)表示第j个航路点与其下一航路点连接而成的线段,Intersect()为相交性判断函数,其值为0表示线段(j+1,j)与单元格cellk不相交。
2.3 改进的SAS求解算法
A*算法是一种经典的启发式搜索算法,被广泛应用于路径搜索问题中。随着研究的不断深入,其得到了不断完善和改进。如SAS算法[7]、动态A*算法(Dynamic Sparse A* Search, DSAS)[8]等。A*搜索通过在每一次迭代中选择搜索空间中启发函数值最小的节点进行扩展。其代价函数形式为
f(x)=a·g(x)+b·h(x)
(4)
其中,g(x)表示从起始位置到当前位置x的真实代价;h(x)表示从当前位置到目标点的预计代价;a,b为真实代价与预计代价的权值。
传统的SAS算法需要事先选定固定步长,算法的效率一定程度受步长选取效果影响。当选取步长较小时,可求得较为精确的解,但是搜索迭代次数变大,搜索效率降低。若步长较大,遇到障碍物较密的情形时,有可能发生绕路,特殊情况下可能导致规划失败。文献[9]对算法进行了改进,其思想是在绝对安全区域使用大步长搜索,在“紧迫环境”下使用小步长搜索,可以在搜索速度与解的质量之间进行折衷,但其通过使用紧迫度阈值判断的方法,由大步长直接跳转至小步长,仍不够灵活,且尚未对大步长与小步长两种情况下搜索子扇形区的数量进行讨论。本文借鉴文献[9]变步长基本思想,设计了连续可变步长和搜索区域联合调整方法,使变步长方案更为合理。
首先对子扇形区数量进行确定。假设UAV速度大小不变,使用下式确定搜索扇面角:

(5)
其中,L为步长,v为UAV速度大小,ωmax为UAV最大角速度,ρ1为调节比例系数。则步长为L时,进行一步搜索扩展的子扇形区数量为
(6)
其中,Δθ为子扇形区扇面角。根据公式(6)可以得出,假设扩展搜索的子扇形区扇面角不变,则待扩展的子扇形区数量与步长成正比。
然后确定搜索步长。定义最大步长与最小步长的关系为
Lmax=Lmin+mmax·ΔL
(7)
其中,Lmax预定义的搜索最大步长,Lmin为最小步长,mmax为最大步长对应的搜索子扇形区数。ΔL为单位变换步长。
从待扩展表中取出节点进行扩展时,首先使用最大步长进行扩展试探,然后根据穿越禁飞区的子扇区数量确定搜索步长:

(8)
其中,mf为使用最大步长试探时落入禁飞区的扩展节点数,ρ2为步长调节系数,满足1≤ρ≤mmax。
其他步骤同传统的SAS算法相同。改进的算法流程图如图2所示。

图2 改进的变步长SAS算法流程图
3 轨迹规划过程
航迹规划过程得到的结果,送至UAV轨迹规划模块的航迹存储单元,每次从中取出一个中间航路点,作为目标点,目标状态的速度、航向角可不做严格约束。以当前时刻状态(位置,速度,航向角)为初始状态,主要考虑UAV性能、协同避碰管理等约束,对UAV进行轨迹规划。UAV到达中间航路点后,再从航迹存储单元中取出下一航路点作为目标点进行轨迹规划过程,不断进行,直至到达UAV航迹最后一个航路点。
文献[11]采用分布式模型预测控制(Decentralized Model Predictive Control, DMPC)结构进行UAV轨迹规划控制。对UAV质点运动学模型离散化后,以UAV速度大小、航向角速度大小为输入,推导出了UAV位置预测模型;以能力-时间组合最优为目标函数,综合考虑无人机性能、协同避碰控制规则、避碰距离等约束条件,建立了MPC滚动优化过程中的单步优化问题模型;设计了UAV避碰管理单元,采用交互图更新机制解决多碰撞管理问题了,形成了一套完整的基于MPC的UAV编队协同轨迹规划方案。本文直接采用其轨迹规划方案。在每一采样时刻,MPC通过求解一个有限时域优化问题,得到系统当前时刻的最优控制序列,从而实现在整个控制时域内的在线闭环控制。UAV协同轨迹规划DMPC控制器滚动优化工作过程如图3所示。

图3 UAV分布式协同轨迹规划MPC工作过程
其中,本机状态由本机传感器获取并传送至MPC控制器,通过预测模型得到带有控制量参数的预测状态,由此得到滚动在线优化问题的一步,通过一定的算法对一步优化问题进行求解后,得到关于UAV速度、角速度大小控制量的优化结果,并将结果输出至UAV动作控制单元。
4 仿真分析
采用计算机仿真验证层次化航迹规划方案的性能。对于路径规划过程,主要对比本文方法与其他方法的性能比较。对于轨迹规划过程,首先通过本文路径规划方法得到多架UAV规划航路,然后将航路作为轨迹规划过程的输入,验证本文方案在多UAV协同轨迹规划过程的可实现性及性能,进而总体验证本文层次化航迹规划方案的有效性。仿真程序运行计算机基本配置:Intel Core i3 3.1GHz、3G内存。仿真平台为MATLAB R2012b。
4.1 路径规划过程仿真
基本参数设置如下:
D=500m,ωmax=0.2rad/s,v=80m/s,ρ1=0.2,Δθ=π/24rad,Lmax=5000m,Lmin=1000m,ΔL=200m,ρ2=1。战场区域为0km×100km的矩形区域,经栅格化后,变为0×200的二维搜索空间,UAV起始点位于(10, 10),终点位于(195, 195)。本文分别对SAS算法使用三类步长方案进行仿真比较。第一类是固定步长,分别取步长为5000m(Lmax)、4000m、3000m、2000m、1000m(Lmin);第二类是文献[9]的双步长阈值切换方法;第三类是本文的改进SAS方法。共计7种步长选取方案,为便于行文,分别命名为方案1至方案7。其中,方案1、方案5、方案6、方案7的计算机仿真结果分别如图4、图5、图6、图7所示。

图4 方案1路径规划结果

图5 方案5路径规划结果

图6 方案6路径规划结果

图7 方案7路径规划结果
7种方案在运算时间、生成路径航路点数、生成航迹长度、open表与close表节点数等更为具体的结果对比如表1所示。
由上述图表对比分析可以得出,传统固定步长的SAS算法大步长搜索时求解速度最快,航路点数最少,close表和open表存储空间占用也最少,但是所得解在四种方案中最差。固定小步长优缺点正好与之相反,求得解较优,但是计算时间、空间占用等均大幅增加。方案6使用的通过阈值来控制在大、小两种步长间切换,经试验仿真,改进效果并不明显,并且仿真中发现,方案3对于阈值的选取要求较高,在阈值选取不精确的情况下,容易导致寻径搜索失败。本文的方案在计算时间、解质量、存储空间占用等性能上介于最大步长SAS算法和最小步长SAS算法之间,与方案3结果相近。但由于每步采用“试探-选择”的方法确定步长,步长的大小根据试探结果在多个离散值上动态选择,解决了SAS算法中确定性步长对于不同环境条件下求解质量不稳定的问题,对于不同条件的规划环境具有非常好的适应性,较之于固定步长SAS,其更适应于环境动态变化或信息部分已知的路径规划。

表1 不同方案下的运行结果对比
4.2 轨迹规划过程仿真
为验证轨迹规划过程的有效性,对多无人机协同轨迹规划过程进行仿真,假定整个飞行过程中UAV速度保持不变。基本参数设置如下:
ΔT=1s,N=20,Nc=10,dif=5000m,ds=500m,


为简化计算,假设MPC的预测控制序列中仅第一项不为0,即MPC预测控制序列中角速度输入序列形如(ω1,0,…,0)。假设UAV获取自身状态信息是完全准确的,即仿真中UAV当前时刻获取的状态等于MPC在上一时刻模型计算输出的本时刻状态。
4架UAV初始信息、终点信息、参数设置等如表2所示。

表2 UAV参数表
其中,第一航路点位置由路径规划阶段计算得出。这里仅对4架UAV从初始状态到第一航路点进行轨迹规划仿真。障碍物设置、区域大小、栅格大小等初始条件与4.1节完全相同。4架UAV的路径规划阶段得到结果如图8所示。

图8 4架UAV航路规划结果
其协同轨迹规划结果如图9所示。
使用航向角变化规则进行分布式自主协同轨迹规划,UAV速度大小保持不变。由图9中可以看出,4架UAV可以有效进行分布式协同轨迹规划, 4架UAV间距始终保持在大于安全间距。
5 结束语
本文采用路径规划与轨迹规划相结合的层次化航迹规划方法,将UAV执行任务中,航线飞行阶段的航迹规划过程,众多的避障约束和UAV协同约束等主要非线性约束部分交由路径规划部分处理,均衡路径规划过程和轨迹规划过程的计算负担。对于路径规划过程使用可变步长机制,改进了传统SAS算法固定步长,难以满足动态环境变化的不足。而轨迹规划过程又可以为UAV在中间航路段过程提供精细的运动控制,而由于此时规划地域范围小,使得轨迹规划计算量大为减轻,从而实现在能够快速得到可行解的情况下实现对UAV的较优控制。仿真结果表明,该方案能够在动态环境条件下得到较优解,算法实时性较好。
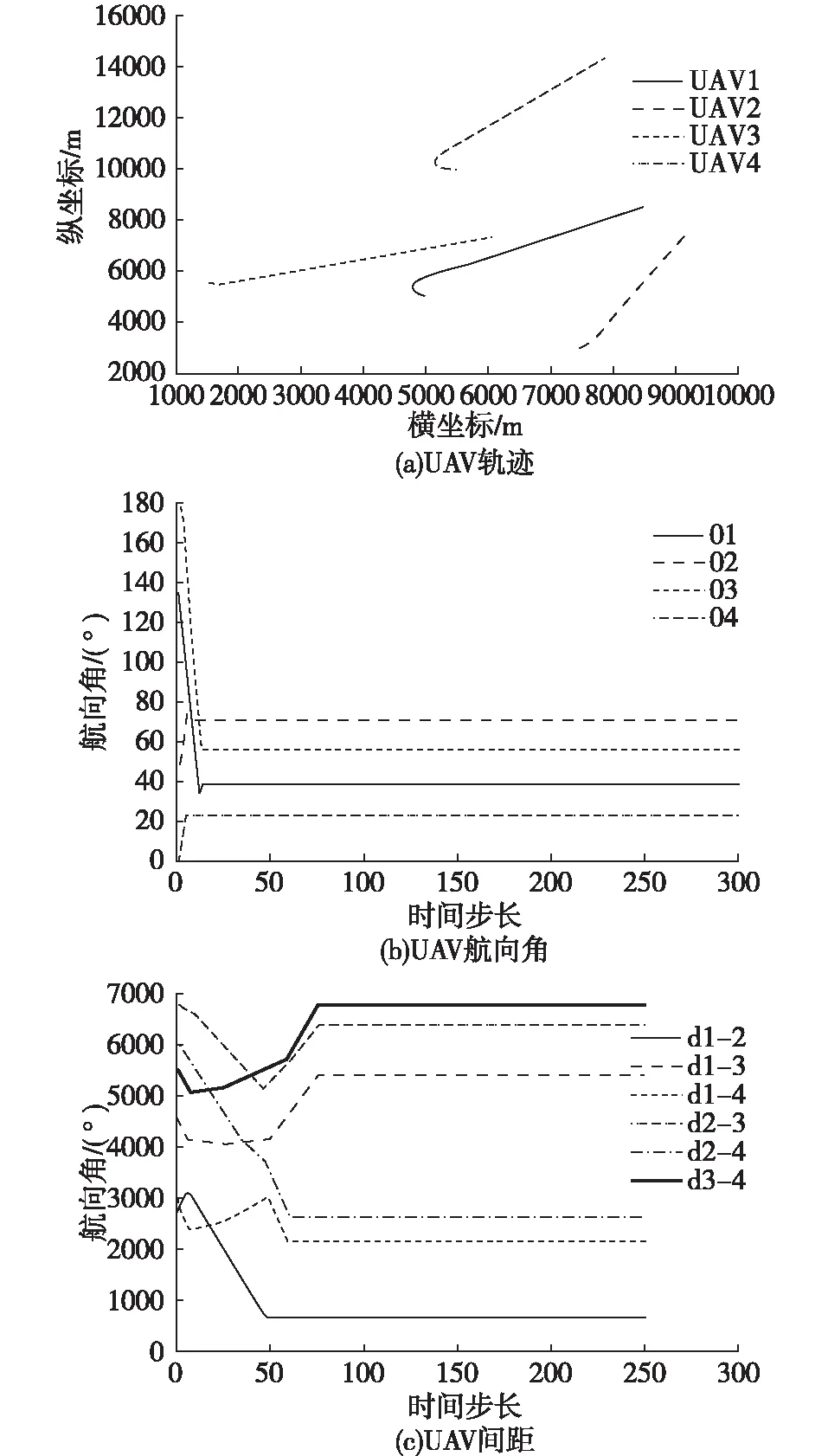
图9 4架UAV协同轨迹规划仿真结果
参考文献:
[1]沈林成,牛轶峰,朱华勇. 多无人机自主协同控制理论与方法[M]. 北京: 国防工业出版社, 2013.
[2]M.Valenti, T.Schouwenaars, Y.Kuwata,E.Feron, J. How. Implementation of a Manned Vehicle-UAV Mission System[C].AAIA Guidance, Navigation and Control Conference, Providence, RI, August 2004,AIAA2004.
[3]Jungert E, Holmes P D. A Knowledge-based Approach to the Shortest Path Problem in a Digtized Map[R]. IEEE Workshop on, Visual Languages, 1998.
[4]王维平,刘娟. 无人飞行器航迹规划方法综述[J]. 飞行力学,2010, 28(2): 6-10.
[5]张煜,张万鹏,陈璟,等. 基于Gauss伪谱法的UCAV对地攻击武器投放轨迹规划[J]. 航空学报, 2011, 32(97): 1240-1250.
[6]谢晓方,孙涛,欧阳中辉. 反舰导弹航路规划技术[M]. 北京: 国防工业出版社, 2010.
[7]SZCZERBA ROBERT J. Robust algorithm for realtime route planning[J]. IEEE Transaction on Aerospace and Electronic Systems(S0018-9251), 2000, 36(3): 869-878.
[8]Guo Jianming, Liu Liang. A study of improvement of D* algorithms for mobile robot path planning in partial unknown environments[J]. Kybernetes, 2010, 39(6):935-945.
[9]黄文刚,张怡,姜文毅,等. 变步长稀疏A*算法的无人机航路规划[J]. 计算机工程与应用,2012, 48(29):206-209.
[10] 魏瑞轩,吕明海,茹常剑,等. 基于 DE-DMPC的 UAV编队重构防碰撞控制 [J]. 系统工程与电子技术,2014, 36(12):2473-2478.
[11] 李相民,薄宁,代进进. 基于模型预测控制的多无人机避碰航迹规划研究[J]. 西北工业大学学报,2017,35(3): 513-521.

