玻璃振动模压中变幅杆高温模态分析及实验研究
余剑武,柳波,罗红,易成,李婵
玻璃振动模压中变幅杆高温模态分析及实验研究
余剑武,柳波,罗红,易成,李婵
(湖南大学国家高效磨削工程技术研究中心,湖南长沙 410082)
为研究应用于光学元件的超声振动模压中变幅杆的高温振动特性,基于纵振波动方程设计所需频率的超声变幅杆,利用Creo软件建立其参数化模型。考虑变幅杆高温下的材料特性变化,结合实验所得数据对高温下的变幅杆进行模态分析,得到其在高温下的谐振频率。分析研究表明,变幅杆谐振频率随着温度的升高而降低。为提升变幅杆高温的下频率稳定性,通过有限元软件对其进行了结构优化设计。按照优化后的尺寸加工出变幅杆,通过实验检测其谐振频率,结果表明,在高温下优化后变幅杆的谐振频率仍稳定在设定频率附近。
高温;变幅杆;谐振频率;玻璃模压
0 前言
玻璃模压成型(Glass Molding Press,GMP)利用高精度热压成型机将软化状态下的玻璃坯料(gobs)在超精密模具中加温加压直接压制成高精度的光学元件。GMP技术开创了大批量、高效率制造光学玻璃元件的新时代,加工对象从非球面透镜扩展到了微结构光学元件的成型。M. Heckele[1]等人认为模压成型可制造出高精度与高品质兼具的产品,是光学元件微结构成形的理想技术,其特点是材料流动距离短与剪切速率低,可避免产生内应力。周天丰[2]等人采用模压成型工艺加工V形槽光学玻璃元件,存在较多的缺陷,尺寸的传递性较差,填充不饱满,影响了光学元件的形状精度和表面质量。
近年来,超声波辅助加工在高温下的应用也越来越广泛,日本 HOYA株式会社在注塑成型过程中用超声振动系统带动模具高频振动,使聚合物熔体的流动性能增加[3]。为了提高微结构光学元件的填充性,J. C. Hung[4]等人开展了超声振动模压设备研究,其研究表明超声振动有助于提高玻璃元件的成形精度。变幅杆是超声加工系统中的主要部分,主要起放大换能器输出机械振动振幅、聚集超声振动能量及匹配超声振动系统阻抗等作用,其振动特性对整个超声加工装置极其重要[5-6]。
本文所涉及的V形微结构光学元件具有几何形状比较复杂、尺寸小、单元数量多等特点,模压后V形微结构容易出现填充不饱满的情况。为了提高其填充性能,提出将超声振动应用于V形微结构的模压成型,因此,探究高温下的超声变幅杆稳定性非常有必要。本文基于解析法[7]设计超声振动模压用变幅杆,考虑高温对TC4材料特性的影响,通过ANSYS对其进行模态分析,获得变幅杆在不同温度下的谐振频率,然后根据仿真结果对变幅杆进行结构优化设计和实验验证,提升高温下变幅杆振动频率的稳定性。
1 应用于玻璃模压的变幅杆设计
1.1 超声振动模压成型
微结构光学玻璃元件的超声振动模压成型原理如图1所示。模具放置于加热腔内,通过加热腔对其进行加热。变幅杆直接与上模具接触,通过上模将高频振动传递给软化的玻璃坯料。
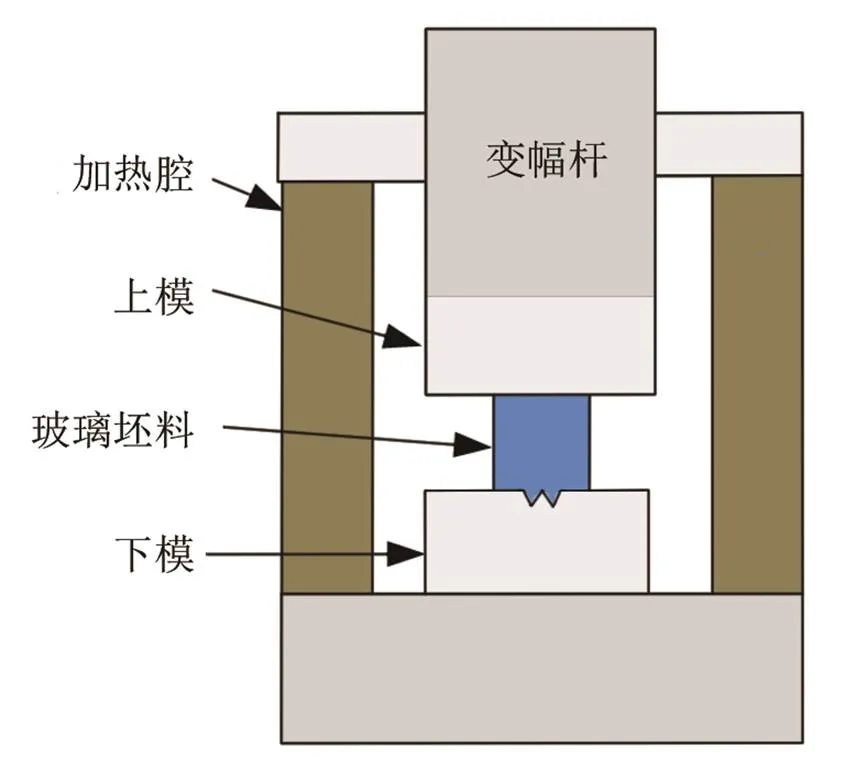
图1 微结构光学元件超声振动模压成型示意图
1.2 变幅杆材料选择
在超声振动模压中,变幅杆一端在加热腔内与高温模具相接触,模具的工作温度为600℃左右,另一端与超声振动系统的压电换能器相连,需保持室温,所以在变幅杆的两端呈现较大的温度梯度分布,此时材料性能参数会因温度分布而发生改变,将影响高温下变幅杆的振动特性。对变幅杆的材料选择要求主要有[8]:(1) 在其工作频率范围内材料的损耗小;(2) 材料的抗疲劳强度高,而且声阻抗率小;(3) 在高温下,要有较好的振动稳定性。因此本研究的变幅杆的材料选择了具有良好高温特性的TC4钛合金,相关性质参数如表1所示[9]。
1.3 超声变幅杆设计
在设计变幅杆时,需考虑模压加热腔的空间限制及模具的尺寸大小和形状。变幅杆的设计采用复合型变幅杆,将其设计为两段式,采用螺纹连接。小端直径与模具直径相同。基于半波长理论进行变幅杆设计,其频率为35 kHz,在谐振条件下,变幅杆纵振波动方程为[10]

表1 钛合金TC4材料参数
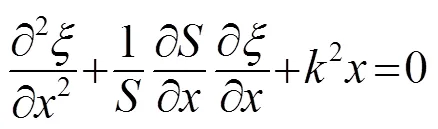
式中:为变幅杆截面积;函数为质点位移函数;=/为圆波数,为纵波在变幅杆中的传播速度。
在等向性固体材料细长杆中,超声波的波速可以由式(2)近似得到:

其中:为波速;为杨氏模量;为材料密度。
图2是用于模压成型的超声振动系统结构示意图,其中振子由压电陶瓷环,前、后端板和预紧螺栓等组成,振子的法兰位于系统振动节点处,用于固定振子。变幅杆设计尺寸如图3所示。

图2 超声振动系统

图3 变幅杆尺寸(单位:mm)
2 变幅杆模态分析
2.1 常温下模态分析
针对常温下的变幅杆进行模态分析,验证变幅杆尺寸设计的正确性。首先利用三维设计软件Creo2.0建立变幅杆三维模型,将模型导入到ANSYS中划分网格,网格划分采用自由划分方式,如图4所示。单元类型采用六面体20节点结构单元solid197,按照表1定义TC4相关材料参数。并在法兰盘施加约束,将法兰盘轴向位移和径向位移设置为0。在频率30~40 kHz范围内进行模态分析,获得4阶模态,对于超声加工而言,理想模态为纵振模态,其中第二阶模态为纵振模态,模态分析结果表明其谐振频率为35 279 kHz,与理论设计谐振频率35 kHz较接近,其位移云图如图5所示。

图4 变幅杆网格划分图

图5 模态分析位移云图
2.2 高温下模态分析
在模压成型中,模具的工作温度高达600℃左右,根据常温设计的变幅杆在高温下的工作频率可能会出现漂移或不能正常起振等不利现象,所以需对高温下变幅杆进行模态仿真分析,以得到其高温下谐振频率的变化数据。变幅杆高温下的模态分析属于热力耦合分析,其分析流程如图6所示,首先需对有限元模型进行稳态热分析,可得到变幅杆的温度梯度分布;然后将此温度梯度分布结果作为初始条件进行结构分析,可得变幅杆受热膨胀后的外形;最后将变幅杆的温度分布及热膨胀后的外形作为初始条件,进行模态分析,即可得知振动系统的谐振频率。
首先进行变幅杆稳态热分析,在超声振动玻璃模压成型中,变幅杆内存在较大的温度梯度分布。为了方便边界条件添加和使分析结果更符合实际情况,因此在系统加热到稳定状态时,测量变幅杆轴向在0、10、20、30 mm处在加热炉内的温度值(图7)。本实验测量了3组模压温度(200℃、400℃和600℃)下变幅杆的实际温度分布情况,实验测定的温度值如表2所示。在稳态热分析中,变幅杆在0、10、20、30 mm四处的横截面温度设定与该处实验测定温度值相同,将变幅杆在加热腔外的另一端的环境温度设定为25℃。仿真分析中加热端只考虑热传导系数(如表1所示),不考虑对流和辐射,得到了变幅杆内的温度梯度分布情况(如图8所示)。

图6 高温下变幅杆模态分析流程

表2 变幅杆的温度实验测定值
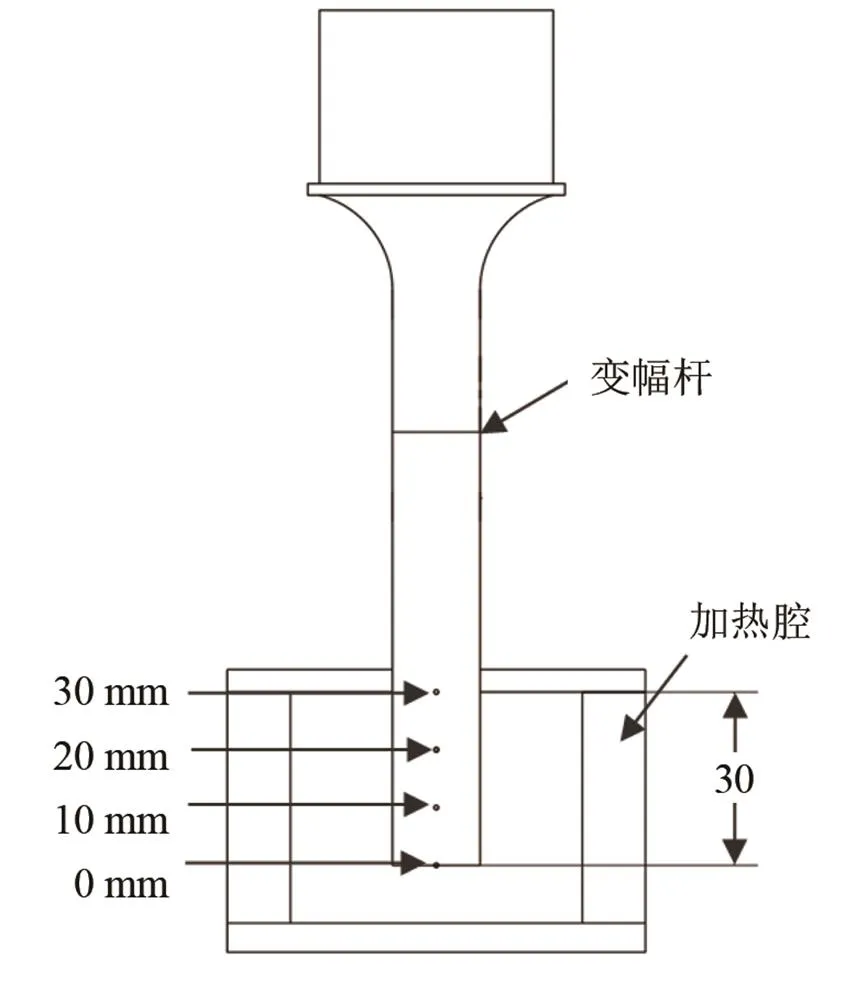
图7 变幅杆测温示意图
在结构分析中,将上述热分析所得的温度梯度分布作为初始条件,由于变幅杆法兰盘位于振动节点位置,因此将法兰盘轴向位移设置为0,以静态结构求解,得到变幅杆的热应力及热膨胀等数值。再以变幅杆的温度梯度分布及热膨胀后的外形作为初始条件,并考虑高温下的材料的参数变化进行模态分析,求得变幅杆谐振频率随温度变化的偏移量。各温度下热膨胀值及谐振频率如表3所示,随着模压温度逐步升高,变幅杆的谐振频率偏移量增大;当模压温度达到600 ℃时,变幅杆谐振频率为32 072 Hz,严重偏移超声振动系统的35 kHz的设定频率。

200℃

表3 各温度下热膨胀值及谐振频率
2.3 高温下变幅杆尺寸优化
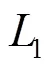
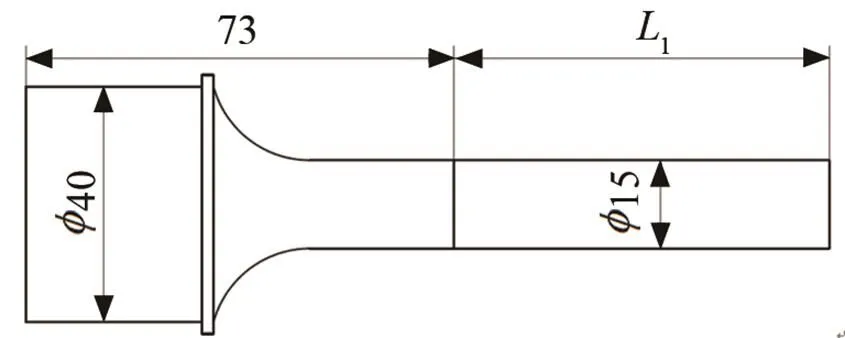
图9 变幅杆尺寸优化示意图(单位:mm)
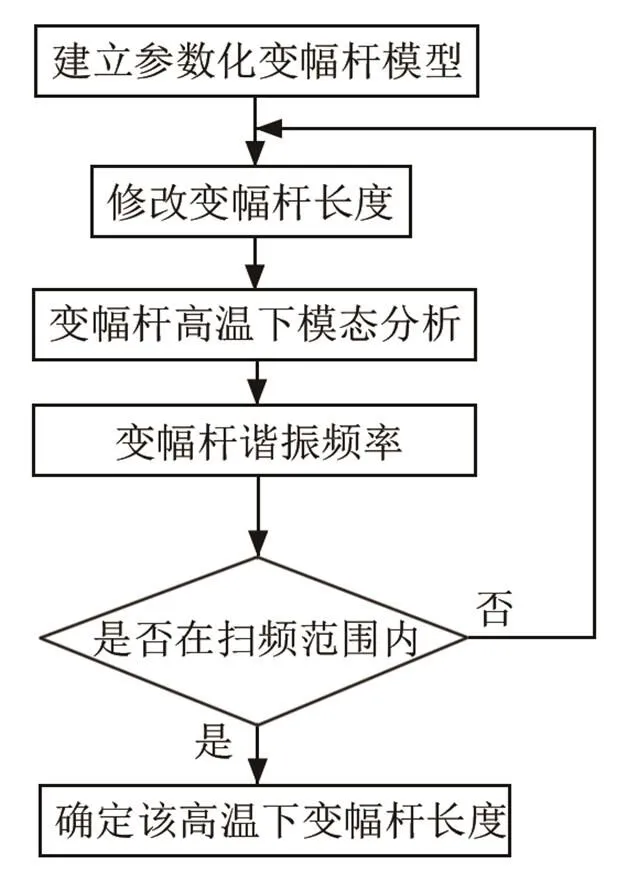
图10 高温下变幅杆尺寸优化设计流程图
通过分析,确定了200、400、600 ℃各温度下的变幅杆最优长度尺寸,优化尺寸后的变幅杆谐振频率如表4所示,其谐振频率都处于设定频率附近,且非常接近理论设计频率35 kHz。
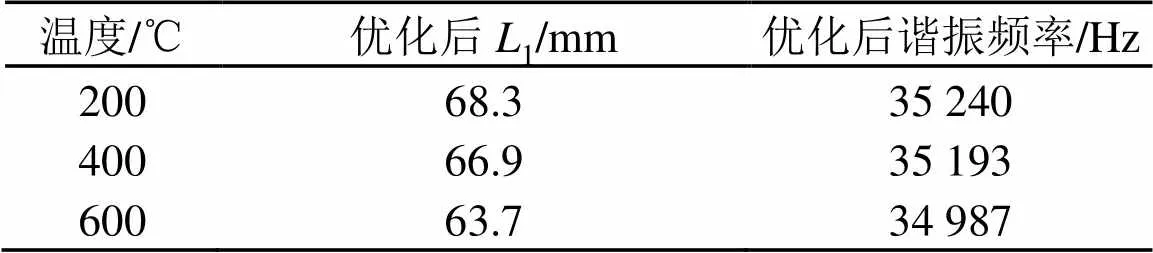
表4 优化后变幅杆尺寸值和谐振频率
3 实验验证
按照尺寸优化后定制出的变幅杆实物如图11所示,振动系统的装配图如图12所示,两截变幅杆采用螺纹连接,为方便变幅杆安装固定,加装了套筒。

图11 200℃和600℃下的变幅杆实物图

图12 超声换能系统
下面将通过实验来验证仿真变幅杆尺寸优化设计的正确性。针对高温下变幅杆的谐振频率检测,采用加热炉对超声变幅杆进行加热,用温度控制器对加热炉内温度进行控制,测量装置如图13所示。超声波发生器将输出信号接入振子,调节输出信号频率并通过阻抗分析仪器(PV520A)检测变幅杆的谐振频率。

图13 谐振频率测量示意图
首先以小信号激励,用精密阻抗分析仪测量出超声振动系统的谐振频率。测得常温下其谐振频率为34.9 kHz,与ANSYS模态仿真分析所得的结果35.2 kHz较为吻合,误差仅在0.7%左右。
在600 ℃下,优化前的振动系统出现了无法起振的情况,说明其谐振频率偏移出设定值35 kHz。为了检测其谐振频率,参考仿真结果(见表3),选用32 kHz频率换能器与变幅杆装配,用精密阻抗分析仪测出振动系统的谐振频率为31.9 kHz,与模态仿真分析所得的结果比较吻合,验证了高温下模态分析的准确性。通过实验分别测出在200、400、600 ℃温度下的优化前后变幅杆的谐振频率。对变幅杆尺寸优化前后的谐振频率进行了对比分析,如图14所示。尺寸优化前变幅杆的谐振频率随模压温度的升高而降低,实验结果与仿真结果的变化趋势基本吻合。尺寸优化后变幅杆的谐振频率基本上都在超声波发生器的扫频范围(35±0.5 kHz)内,不随温度的升高而较大幅度降低,满足设计要求,且实验结果与仿真结果较为吻合,表明优化后的变幅杆的谐振频率稳定性得到了提高。同时可知,谐振频率的仿真结果和实验结果存在一定偏差,这可能与仿真分析中忽略变幅杆中的螺纹连接有关。

图14 实验结果与仿真结果对比
4 结论
高温下变幅杆振动频率稳定性研究对于超声振动辅助玻璃模压具有重要意义:(1) 本文通过理论计算和模态分析相结合的方法,得到了变幅杆的谐振频率随模压温度的升高而下降的变化趋势;(2) 从提高变幅杆高温下振动特性的稳定性出发,对不同模压温度下的变幅杆的结构尺寸进行了优化设计;(3) 按照优化后的尺寸加工不同模压温度下的变幅杆,实验检测的谐振频率与仿真分析结果十分接近,且在高温下仍稳定在设定的超声波扫频频率附近,变幅杆的振动稳定性得到提升,为高温下变幅杆的设计提供了参考。
[1] HECKELE M, BACHER W, MüLLER K D. Hot embossing-The molding technique for plastic microstructures[J]. Microsystem Technologies, 1998, 4(3): 122-124.
[2] ZHOU T F, YAN J W, MASUDA J, et. al. Numerical and experimental investigation on the transferability of ultraprecision glass molding press for microgrooves[C]//Asian Symposium for Precision Engineering and Nanotechnology (ASPEN2009), Nov. 11-13, 2009, Kitakyushu, Japan, 2009: 1-5.
[3] SAITO K, INOUE K, SATO A, et al. Molding method and molding device utilizing ultrasonic vibration and optical lens: European, EP1621315A1[P]. 2006.
[4] HUNG J C, TSAI Y P, HUNG C. Development of a new apparatus for ultrasonic vibration-assisted glass hot embossing process[J]. Precision Engineering, 2013, 37(1): 222-227.
[5] 赵明利, 程雪利, 赵波. 带工具头超声变幅杆节点定位偏差问题分析[J]. 声学技术, 2013, 32(3): 253-256. ZHAO Mingli, CHENG Xueli, ZHAO Bo. Research on the node localization deviation of the ultrasonic amplitude transformer with tool head[J]. Technical Acoustics, 2013, 32(3): 253-256.
[6] 张向慧, 钱桦. 旋转超声加工振动系统的研究[J]. 振动与冲击, 2010, 29(4): 218-221. ZHANG Xianghui,QIAN Hua. Research on the vibration system of Rotary ultrasonic machining[J]. Journal of Vibration and Shock, 2010, 29(4): 218-221.
[7] 贺西平, 高洁. 超声变幅杆设计方法研究[J]. 声学技术, 2006, 25(1): 82-86. HE Xiping, GAO Jie. A review of ultrasonic solid horn design[J]. Technical Acoustics, 2006, 25(1): 82-86.
[8] 潘巧生, 刘永斌, 贺良国, 等. 一种大振幅超声变幅杆设计[J]. 振动与冲击, 2014, 33(9): 1-5. PAN Qiaosheng, LIU Yongbin, HE Liangguo, et al.Design of an ultrasonic horn with high amplitude of longitudinal vibration[J]. Journal of Vibration and Shock, 2014, 33(9): 1-5.
[9] 王振东, 林兴照, 武希哲,等. TC4钛合金全面性能测试[J]. 稀有金属材料与工程, 1982(8): 49-50.
WANG Zhendong, LIN Xingzhao, WU Xizhe, et al. TC4 titanium comprehensive performance test[J]. Rare Metal Materials and Engineering, 1982(8): 49-50.
[10] 林仲茂. 超声变幅杆的原理和设计[M]. 北京: 科学出版社, 1987. LIN Zhongmao. Theory and design of ultrasonic horns[M]. Beijing: Science Press, 1987.
High temperature modal analysis and experimental study of the ultrasonic horn for glass vibration molding
YU Jian-wu, LIU Bo, LUO Hong, YI Cheng, LI Chan
(National Engineering Research Center for High Efficiency Grinding, Hunan University, Changsha 410082, Hu’nan, China)
In order to understand the vibration characteristics of the ultrasonic horn for glass vibration molding at high temperature, a horn with a required frequency is designed based on longitudinal vibration theory, and a parameterized model of the horn is established with Creo2.0 software. Considering the material properties change of the horn at high temperature, the corresponding modal analysis is made, the resonance frequency of the horn is obtained by simulation analysis and the resonance frequency decreases with increasing temperature. In order to improve the frequency stability of the horn at high temperature, structural optimization design is carried out by finite element software. The horn is manufactured according to the optimized size, and the resonance frequency is tested by experiment. The experimental results indicate that the resonance frequency of the horn remains stable near the set frequency at high temperature.
high temperature; horn; resonance frequency; glass vibration molding
TB559
A
1000-3630(2018)-01-0051-06
10.16300/j.cnki.1000-3630.2018.01.009
2017-02-22;
2017-04-15
国家自然科学基金资助项目(51275165)
余剑武(1968-), 男, 湖南冷水江人, 博士, 教授, 博士生导师, 研究方向为高速/超高速磨削技术及数控装备, 精密与超精密加工技术及装备。
余剑武, E-mail: yokenbu@hotmail.com

