基于改进遗传算法的多目标优化生产调度模型

郭　梅，李西兴

(1.山西北方晋东化工有限公司，山西 阳泉 045000；2.湖北工业大学 机械工程学院，湖北 武汉 430068)

随着计算机科学和信息技术的不断发展，制造物联网、云计算、大数据和智能制造等先进制造技术和管理思想不断被提出和应用，特别是中国制造2025战略为中国制造企业指明了发展方向。作为订单任务制造执行过程管理和控制的关键问题——生产调度问题(production scheduling problem，PSP)一直是机械制造企业中管理者最为关心的，它属于NP(nondeterminism polynomial)问题[1]。目前，随着管理科学、计算机科学和信息科学等相关学科的不断发展，众多专家学者从不同的方面对生产调度问题开展了针对性的研究[2-3]，主要包括生产调度模型的构建与优化、生产调度目标的求解(包括一般算法和优化算法)、生产调度平台的设计开发和应用[4-6]。笔者在已有研究的基础上，以机械制造企业作为研究背景，

首先分析了企业内部在生产制造执行过程中存在的生产调度问题，其次构建了基于成本、平均完工时间和延迟概率的多目标生产调度优化模型，并对传统遗传算法加以改进作为模型的求解算法，最后通过实例验证模型和算法的有效性。

1　机械制造企业关键零部件生产调度问题分析

1.1　机械生产流程分析

当前机械制造企业的生产模式主要是按订单制造(make-to-order，MTO)，企业根据内部以及外部现有生产资源制定生产计划，安排生产加工，在制作过程中会遇到机器故障、人员调整等突发事件，此时生产调度将决定下一步工作任务的完成方式与路线，具体的生产流程如图1所示。

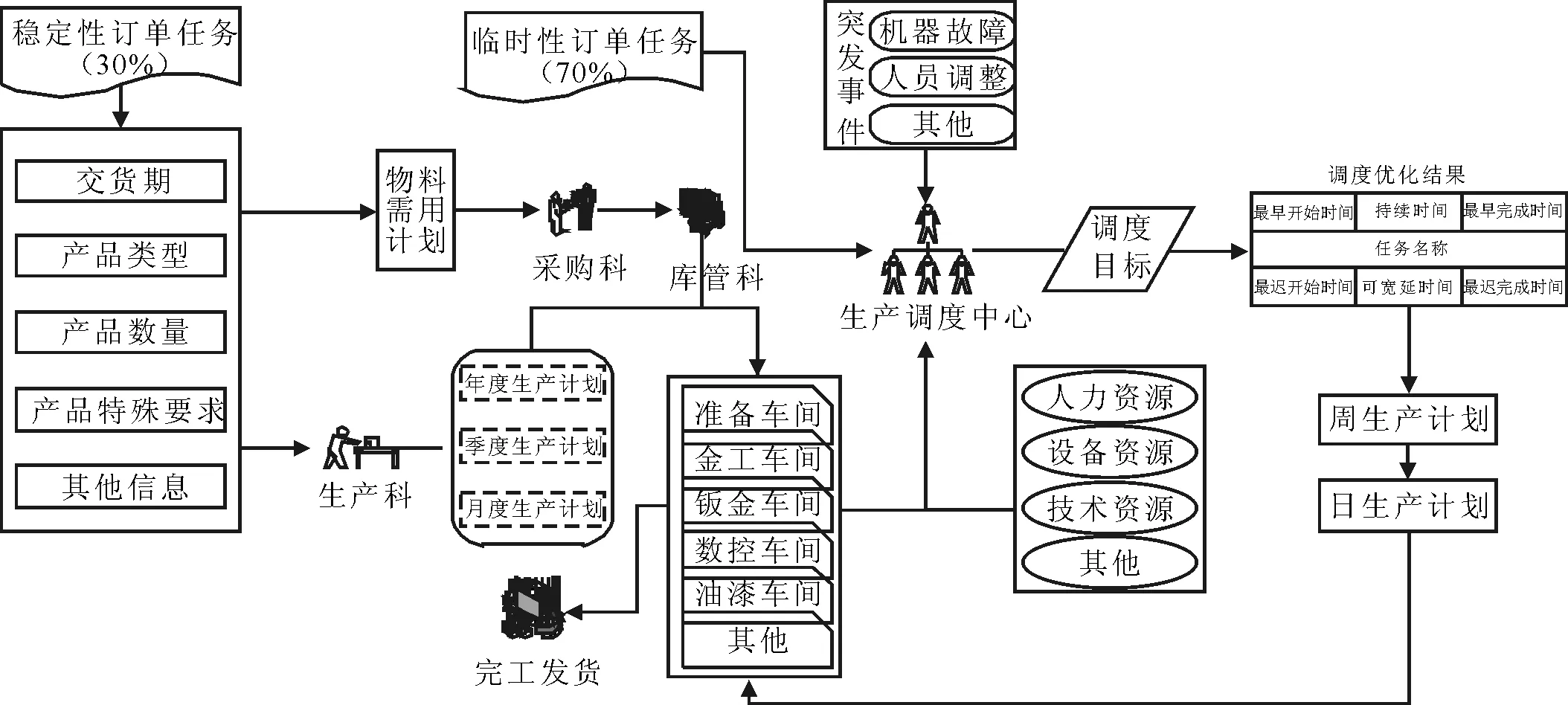
图1　机械制造企业生产流程

1.2　生产调度问题分析

在生产管理中首先要根据现有资源来合理调度主要零部件的生产加工任务，目前主要存在的调度问题有以下几个方面：

(1)调度信息不及时，传递不准确；

(2)调度次数多，周期有效性短；

(3)调度柔性不足；

(4)调度标准不统一。

当前市场竞争环境变得越来越激烈和复杂，客户的个性化需求也越来越突出，这对企业整体的生产管控结构带来重要影响，传统的管控方法不再适合。面对这种情况，机械制造企业对于生产管控的变更将更依赖于订单产品的准时交货率和订单产品的利润率，二者之间是相辅相成的。因此针对上述问题笔者将从以下两个方面开展研究：

(1)构建面向机械制造企业的基于生产成本、平均完工时间和延迟概率的多目标生产调度优化模型；

(2)引入一种基于聚类轮盘赌选择方法的双阶段遗传因子改进遗传算法(improved genetic algorithm，IGA)来求解该生产调度优化模型。

2　生产调度优化模型的构建

2.1　模型假设条件

针对上面提到的问题，笔者提出基于生产成本、平均完工时间和延迟概率的多目标生产调度优化模型，在构建优化模型前作出如下假设：

(1)订单任务信息、加工设备信息、人员信息和其他基本信息在制定生产调度时(假设为0时刻)都是已知的；

(2)每一个加工设备一次最多只能加工一个零部件，且一旦开始加工某一零部件必须完成加工后才能继续加工该零部件的下道工序或者是其他零部件的某道工序；

(3)每一个零部件一次最多只能被一个加工设备加工；

(4)每一个零部件包含若干道加工工序，且工艺路线一旦确定就不得更改；

(5)零部件在各个设备之间运输、装夹、卸载时零部件的大小不做考虑，只考虑对应时间；

(6)不同零部件之间没有加工优先级之分；

(7)加工设备的损耗成本(即折旧成本)在该优化模型中不作考虑。

2.2　优化模型的建立

笔者构建基于总生产成本TC、平均完工时间ACT和延迟概率DP的多目标优化模型F，这样既满足客户交货期的需求，又符合企业的自身利益。根据构建模型时的假设条件，构建数学模型如下:

F=Wtc×TC+Wact×ACT+Wdp×DP

(1)

式中：Wtc、Wact和Wdp分别为TC、ACT和DP的权重值，并满足Wtc+Wact+Wdp=1。

(1)将总生产成本划分为工序成本PC、运输成本TrC、延期成本DC。

TC=PC+TrC+DC

(2)

其中，工序成本PC主要是针对机械零部件在机加工的过程中常用到的工序备、车、铣、磨、镗、钻、煮黑、喷丸、油漆等工序中产生的成本。在计算工序成本时常采用基于工时的计算方式，即以技术部给定的加工工时乘以企业内部规定的单元工时价格。因此工序成本的计算公式如下：

(3)

pijk=λ×pjk

(4)

式中：n为零件数；m为工序数；pijk为零部件i的第j道工序在加工设备k上的加工成本；pjk为零部件i的第j道工序在加工设备k上的单位加工成本。

运输成本TrC主要包括两方面：一方面是零部件在不同加工设备间加工时会造成零部件的转运，从而引起转运成本，规定单位转运成本是固定不变的，在进行转运工作时不考虑零部件的大小，只考虑转运距离；另一方面是零部件的装夹和卸载成本，规定零部件的装夹和卸载的单位成本是固定不变的，在进行装夹和卸载工作时不考虑零部件的大小，只考虑装夹和卸载的总时间。运输成本的计算公式如下：

(5)

(6)

Lijk=Timeijk×Unit_L

(7)

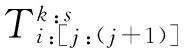
由于在实际的生产加工过程中会出现临时订单、机器故障、人员调整等情况，从而造成原加工任务中部分任务的延期完工，延期完工将给企业带来延期成本，延期成本的计算公式如下：

(8)

Delayi=ceil((CTi-OTi)/8)

(9)

s.t. 如果Delayi<0,则Delayi=0；否则Delayi值不变。

式中：Delayi为零部件i的延期时间；“8”为企业规定的每天8小时工作时间长度(由于企业中在计算延期成本时通常是以天作为延期单位，而零部件的完工时间是以小时为单位，因此为了将完工时间小时转换为天，采用公式(9))；CTi为零部件i的实际完工时间，OTi为零部件i的规定完工时间；Unit_Di为零部件i的单位延期成本；ceil(x)为取整函数，输出结果为比x大的最小整数。

平均完工时间是所有加工任务的整体加工时间之和除以加工任务的数量，具体如下：

(10)

延迟概率是指延迟总加工任务数除以加工任务的数量，具体如下：

(11)

s.t.如果Delayi=0,则qi=0，否则qi=1。

3　基于聚类轮盘赌选择方法的双阶段遗传因子改进遗传算法

遗传算法是根据自然界的“优胜劣汰”的规则首次由J.Holland教授提出，基本思想是将每一代较优的个体保存到下一代中，这样在规定的求解代数后将获得近似最优解。笔者提出利用聚类轮盘赌选择方法来求解初始化种群，保证了初始化种群的多样性，同时针对过早收敛和容易陷入局部最优解的问题，笔者提出分段遗传算子，即在实际的计算过程中若连续Ncontinuous代没有产生新个体时，将分别改变遗传算子的值，从而进一步提高种群的多样性，降低优良基因丢失的可能性。具体的改进遗传算法流程如图2所示。

3.1　基于聚类轮盘赌选择方法的种群初始化方法

传统的轮盘赌选择方法是一类基本的随机选择法，它容易引起算法的过早收敛和陷入最优解，聚类轮盘赌的思想，即将个体按照其适应度值的大小进行分组，然后按照传统轮盘赌的基本思想进行选择，降低某一类超级个体的数量，保证初始种群的多样性，初始种群数定义为Initial_Pop。

(1)依据个体适应度值的大小对初始化种群进行分组，分组的个数即聚类数H，满足公式gen=CF1∪CF2∪…∪CFH，同时以随机率参数rH设定对应的初始聚类中心(f1,f2,…,fH)；

(2)对于群体中的每一个体按照个体与聚类中心之间相邻距离最近的原则分别对每一个个体进行聚类，如果fi-fh=min|fi-fh|,fh∈(f1,f2,…,fH)，则i∈CFh；

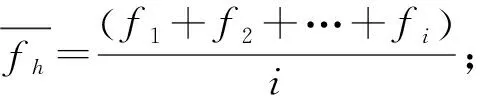
(4)如果新的聚类中心与上一个聚类中心相同，则输出H个聚类，否则转步骤(2)。

3.2　编码和解码

根据优化模型的需求，采用基于待加工任务编号、加工工序编号、加工设备编号的混合十进制编码方法，具体编码和解码规则说明如表1所示。编码和解码示例如表2所示。

表2中给出了3个零部件相应的加工工序、工艺线路以及满足条件的加工设备和对应加工时间的编码样式。

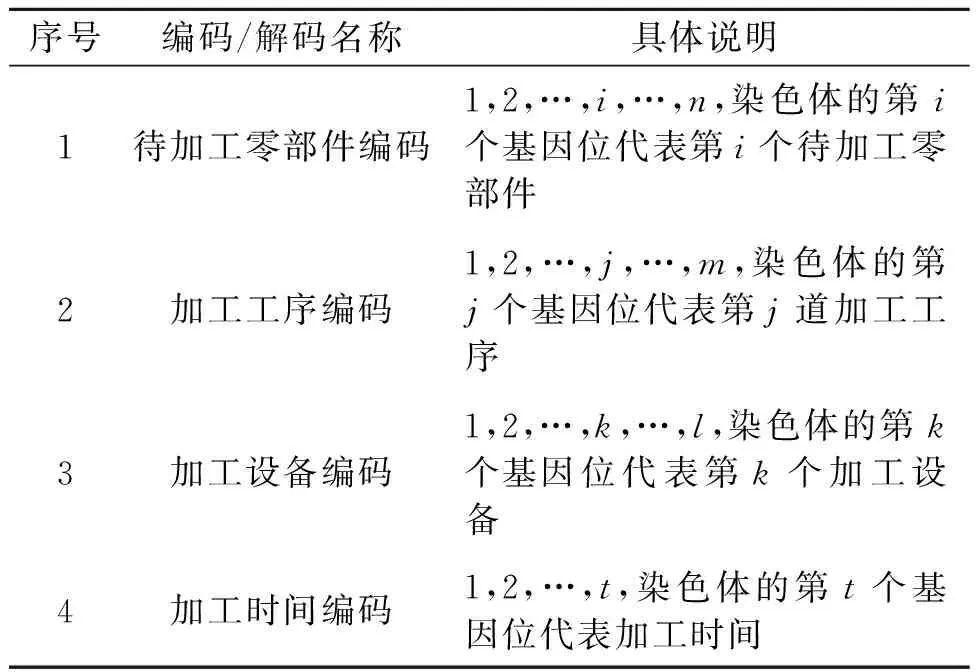
表1　编码和解码规则说明

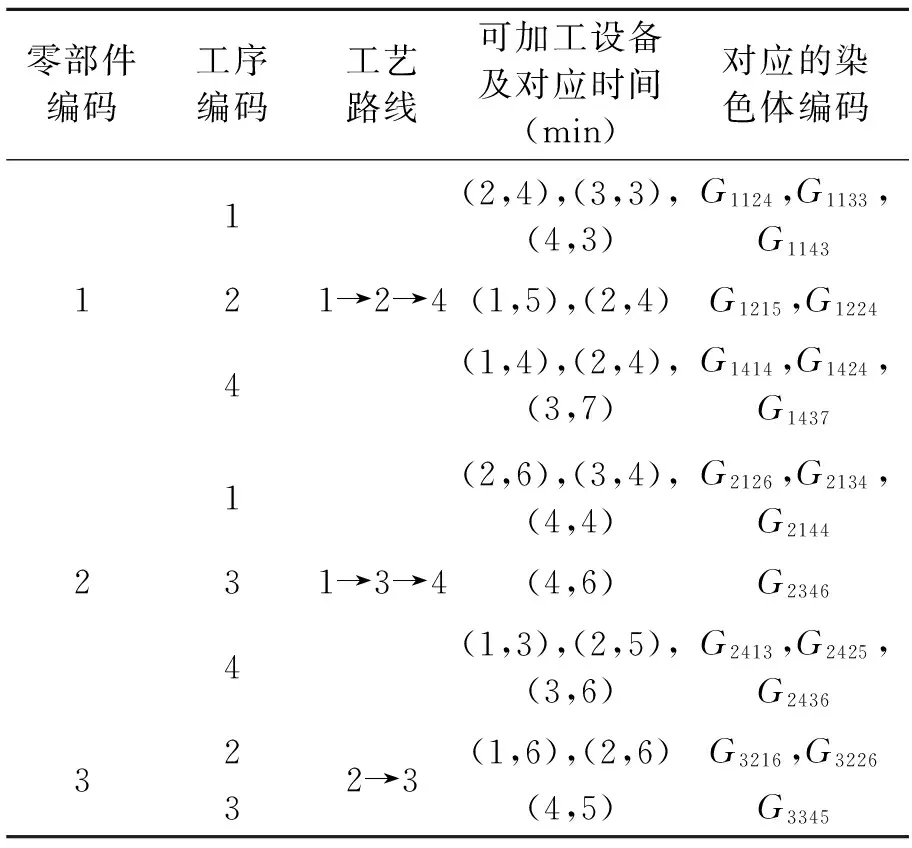
表2　编码和解码示例说明

在解码时，根据染色体编码时的规则解读相应的数据信息，如一个染色体G1124表示零部件1的第1道工序在加工设备2上进行加工，需要消耗的加工时间为4 min。

3.3　适应度函数

适应度函数主要是为了评估个体的优劣性而设定的，通常它是根据目标函数演化而来，在本文中由于目标函数F是最小化多目标优化问题，且各目标单位不同，因此在设定适应度函数时要对其进行标准统一化，如式(12)所示。

f(x)=F=Wtc×TC(x)′+

Wact×ACT(x)′+Wdp×DP(x)′

(12)

(13)

式中：TCm、ACTm和DPm为同一代中所有样本染色体的均值；TCs、ACTs和DPs为同一代中所有样本染色体的标准差。

3.4　遗传算子

遗传算子主要包含选择算子(selection operator，SO)、交叉算子(crossover operator，CO)和变异算子(mutation operator，MO)，主要作用是保证个体的多样性，降低算法陷入局部搜索的概率。

选择算子SO采用聚类轮盘赌的方法对个体进行选择操作，其中选择概率定义为ps。

交叉算子CO对不同染色体的单个或多个相同基因位进行交叉重组，生成新的染色体，其中交叉概率定义为pc，笔者采用优先级交叉操作方法完成父代个体(Parent)交叉生成新的子代个体(Offspring)，具体过程如图3所示。

图3　交叉算子

变异算子MO对于染色体的基因位进行变异重组生产新个体，但变异的范围必须在染色体原有基因范围内，其中变异概率定义为pm，且pm的值通常小于pc，笔者采用翻转变异方法实现染色体的变异操作，如图4所示。

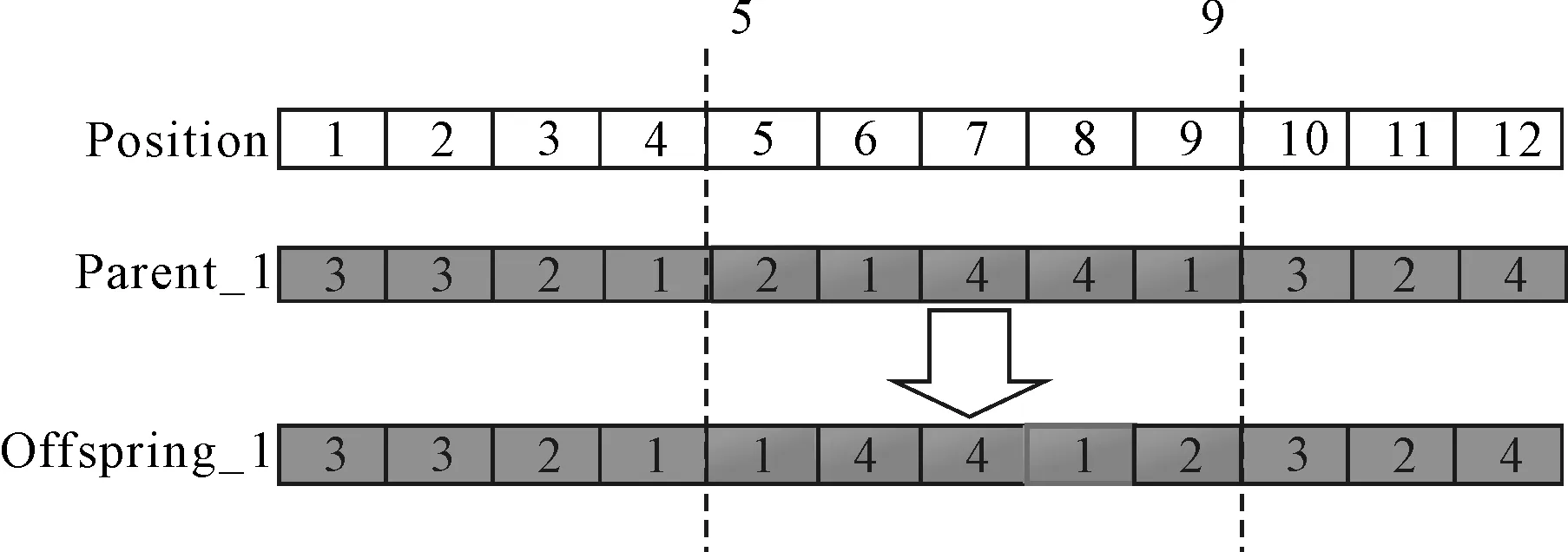
图4　变异算子

3.5　终止条件

由于多目标优化求解过程中很难获得最优解，通常都是以近似最优解作为最终输出，因此为了防止避免算法求解过程中的不断循环，常设定算法最大迭代次数max_Iterations，当算法的实时迭代次数gen大于max_Iterations时算法跳出循环，算法终止并输出近似最优解。即终止条件为：

gen>max_Iterations

(14)

4　算法实例

为了验证模型和算法的有效性，首先搭建基于Matlab2013a的仿真模型，同时根据某机械制造企业的实际生产调度情况进行实例验证。在机械制造中，关键零部件的生产加工对于整机的装配完工和发货有着重要影响，文中表3、表4和表5分别对应着工序基础信息、零部件基础信息和算法参数。由于同种类型加工设备(和工序类别一致)通常放置在相同加工车间中，因此它们之间的距离可以忽略不计，即不考虑同种类型加工设备之间的运输成本。表6中的距离表示不同类型加工设备之间的距离，同时对于单位转运成本Unit_T和单位装卸成本Unit_L分别设定为0.05元/m和0.1元/min。

表3　加工工序基础信息

表4　零部件基础信息

表5　算法参数设定

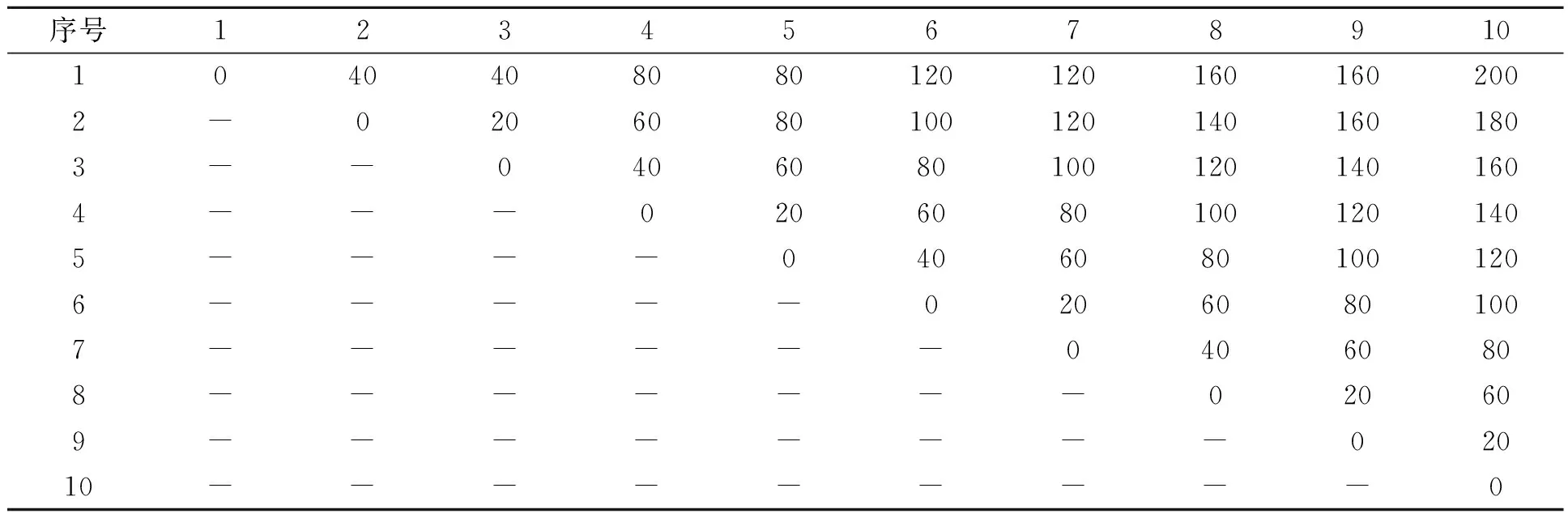
表6　加工设备之间距离　m

为了尽可能的获取到最优解，对算法进行了20次测试，得出最优适应度值为1.462，平均求解耗时为7.74 s，具体的收敛曲线如图5所示，图6列出了对应的Gantt图。笔者在传统遗传算法的基础上分别引入聚类轮盘赌方法和分段遗传因子方法，表7列出了单一聚类遗传算法(Cluster-GA)和传统遗传算法(Traditional-GA)的对比结果，同时与粒子群算法(PSO)进行对比，各自对应的进化曲线如图5所示。首先聚类轮盘赌选择方法比传统的随机初始化方法和单一轮盘赌选择方法提供了更优的初始化种群个体，在保证初始种群多样性的同时确保相对最优种群个体的数量；其次利用分段遗传算子方法可以降低算法迭代过程中陷入局部最优解的可能性，并且最大限度地避免全局近似最优解的丢失，使得IGA在求解的速度和有效性方面更好。为了更好的与以上3种算法作比较，应用方差分析法的理论来验证各个算法对应的可靠性，通过置信水平值为5% 的LSD(least-significant difference，最小显著性差异法)来分析各个方法的差异，结果如图7所示，IGA方法的可靠性优于其他3种方法。

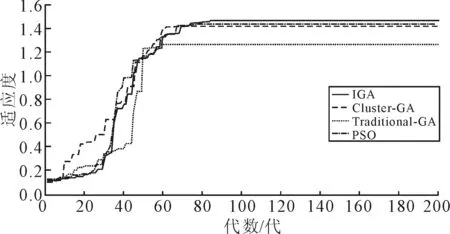
图5　收敛曲线对比分析

图6　近似最优解Gant图

算法最优解计算时间/s获取最优解代数最优解比例/%Traditional-GA[7]1.26110.436040Cluster-GA[8]1.4138.636470IGA1.4627.748480PSO[9]1.4337.987770

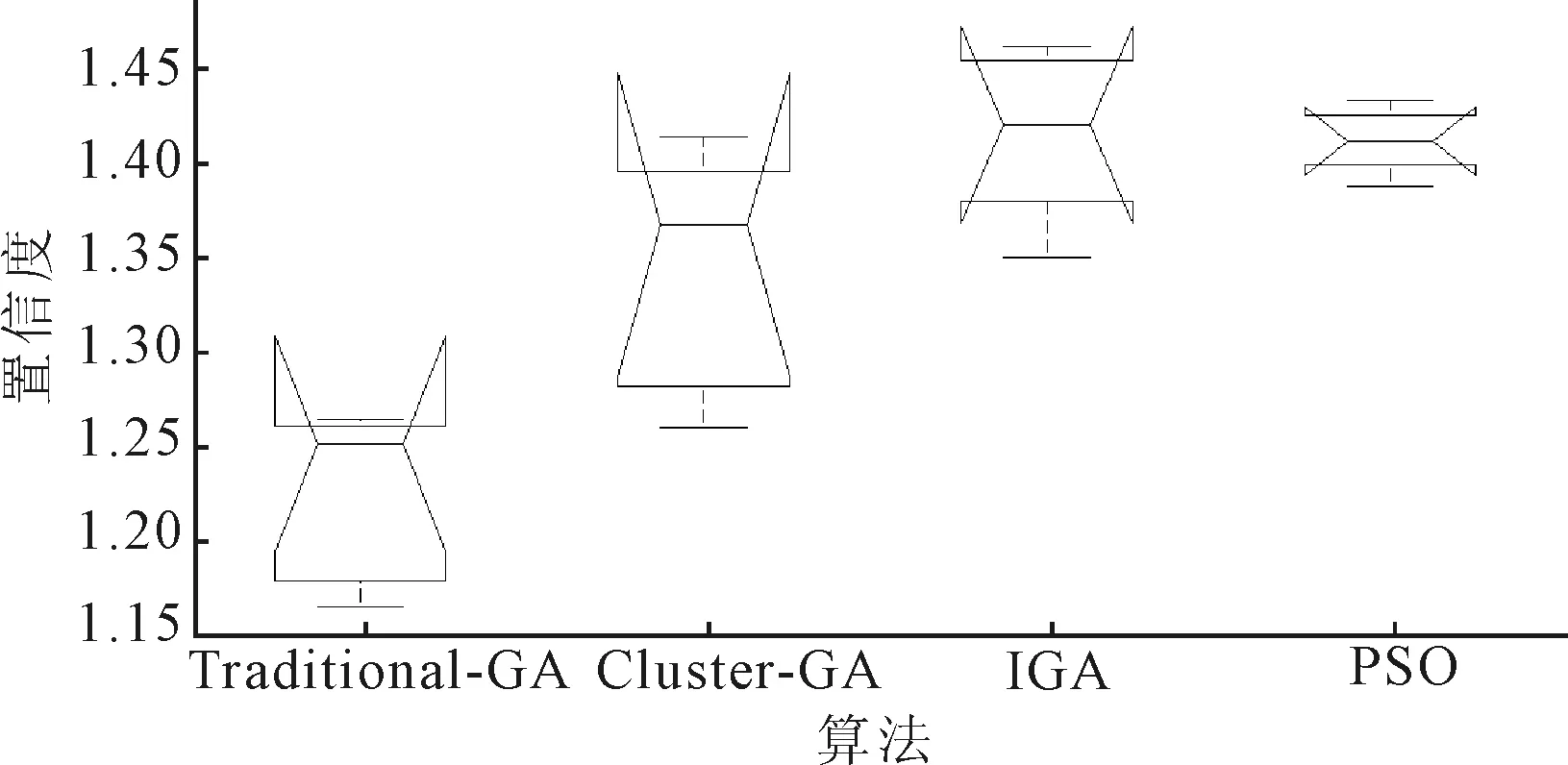
图7　置信度评估

5　结论

由于机械制造企业的生产模式发生了变化，为了快速响应市场变化更好地满足客户个性化需求，首先分析了当前企业的生产流程及生产调度中存在的问题，其次构建了基于生产成本、平均加工时间和延迟概率的多目标优化调度模型，提出基于聚类轮盘赌的双遗传因子的改进遗传算法，并对模型进行求解，最后通过实例数据测试和对比分析，证明了该方法的有效性和可行性。该理论模型和算法的特点和优势包括以下两个方面：

(1)客户满意度和生产成本是当前机械制造企业关注的重点，因此该模型以订单任务中关键零部件的平均加工时间、生产成本和延迟概率作为优化目标，满足企业的实际要求；

(2)传统遗传算法存在容易过早收敛和陷入局部最优解的缺点，笔者分别通过应用分段遗传算子和聚类轮盘赌的种群初始化方法来解决上述问题，从而获取了更好的近似最优解。

参考文献：

[1]Liang Gao, Guohui Zhang, Liping Zhang, et al. An Efficient Memetic Algorithm for Solving the Job Shop Scheduling Problem[J]. Computers & Industrial Engineering, 2011,60:699-705.

[2]刘琼,张超勇,饶运清，等.改进遗传算法解决柔性作业车间调度问题[J].工业工程与管理，2009,14(2):59-65.

[3]巴黎,李言,曹源,等.考虑批量装配的柔性作业车间调度问题研究[J].中国机械工程，2015,26(23):3200-3207.

[4]杨晓梅，曾建潮.遗传算法求解柔性Job-Shop调度问题[J].控制与决策，2004,19(10):1197-1200.

[5]张铁男,韩兵,于渤.生产能力约束条件下的柔性作业车间调度优化[J].系统工程理论与实践,2011,31(3):505-509.

[6]张国辉,党世杰.遗传算法求解低碳柔性作业车间生产调度问题[J].组合机床与自动化加工技术,2016(11):141-143.

[7]Alebachew D Yimer, Kudret Demirli. A Genetic Approach to Two-phase Optimization of Dynamic Supply Chain Scheduling[J]. Computers & Industrial Engineering, 2010,58:411-422.

[8]杜百岗,郭顺生,彭兆,等.集团制造多主体外协订单任务制造资源配置[J].计算机集成制造系统,2015,21(2):455-466.

[9]祁文博,郭顺生,赵国，等.改进初始化方法求解柔性作业车间调度问题[J].数字制造科学，2017，15(4)：192-196.