基于IPSO-BP神经网络的锂电池SOC预测

罗晓东

(1.武汉理工大学 汽车工程学院，湖北 武汉 430070；2.武汉理工大学 现代汽车零部件技术湖北省重点实验室，湖北 武汉 430070)

锂离子电池由于其质量轻、单体能量密度大、充电时间短等优点，已被各大厂商广泛运用于纯电动汽车[1]，而动力电池系统中SOC(state-of-charge)的精确估算具有十分重要的现实意义。

当前预测SOC的方法有：开路电压法、安时积分法、放电实验法等，这些是基于电池内部的物理化学模型，需要深入研究电池内部的电化学反应、电池电化学材料的特性，以及失效机理，从而建立起电池的物理失效模型。模型内部有大量经验参数，精度不高[2-5]，而且建模时间长，过程繁杂。另一大类是基于数据驱动,利用人工神经网络，不需要直接确定输入量和输出量的关系，而将其模糊化，其中BP(back propagation)神经网络结构简单，可调整参数多，且易于操作，因此笔者采用BP神经网络对SOC进行预测[6]。但由于人工神经网络虽泛化能力强，却容易陷入局部最优。笔者分别引入粒子群(particle swarm optimization,PSO)算法和遗传算法(genetic algorithm,GA)对BP的权值和阈值进行优化，并将结果进行比较，得出更优的算法模型。

1　BP神经网络预测SOC

1.1　BP神经网络

BP神经网络是一种由信息的正向传播和误差反向传播组成的多层前馈网络[7]。网络由三层组成，输入层，隐含层，输出层，其中对于隐含层，可分为单隐含层和多隐含层，多隐含层网络泛化能力强，预测精度高，但增加了复杂程度导致训练速度下降，因此具体问题需具体分析。对于预测SOC，可采用三层神经网络，如图1所示。输入层选取影响SOC最重要的3个参数：放电电压(U)、放电电流(I)，环境温度(T)，输出层为SOC，隐含层个数可通过下列经验公式判断，算出m为7。

(1)

(2)

m=2n+1

(3)

式中：m为隐含层个数；l为输入层个数；n为输出层个数；α为1～10之间的调节常数。

图1　BP神经网络结构图

1.2　BP神经网络学习过程

BP神经网络学习算法的基本原理是梯度下降法，中心思想是调整神经网络结构的连接权值与阈值，从而使误差达到理想状态。整个学习阶段按顺序分为两部分：正向传递和误差的反向传递。在第一阶段，输入量首先经过输入层，传递至隐含层，经过每一层的处理，传向输出层，每一层级影响范围有限，只能影响下一级神经元状态。当误差达不到所设置的期望误差时，进入第二阶段，进行反向传播，误差信号会按照原来的通路返回，修改各层神经元的权值，使误差达到最小，具体过程如下：

(1)初始化网络。由系统的输入输出序列(x,y)确定各层节点数，初始化各层间连接权值ωij,ωki，初始化隐含层阈值a,输出层阈值b,给定学习速率及神经元激励函数。

(2)BP神经网络的前馈计算。由输入参数组成的矩阵，按式(4)，式(6)分别计算隐含层和输出层的输出。

(4)

式中：H为隐含层输出；M为输入层节点数量；i为隐含层节点数；ωij为输入层和隐含层之间的连接权值；q为隐含层节点；f为隐含层激励函数；a为隐含层阈值，其中激励函数形式多样，本文选取的激励函数如下：

(5)

(6)

式中:O为输出层输出；b为输出层阈值；ωki为输出层和隐含层之间的连接权值；L为输出层节点数量。

(3)按照式(7)计算网络的输出O和期望输出y′的误差e。

(7)

(4)连接权值更新。由输出误差e，按照式(8)和式(9)更新神经网络的连接权值ωij，ωki。

j=1,2,…,M；i=1，2，…，q

(8)

ωki=ωki+ηHiek

i=1,2,…，q；k=1,2,…，L

(9)

式中：η为学习速率。

(5)BP神经网络的阈值更新。与权值调整相似，通过误差e和式(10)调整隐含层和输出层的阈值a，b。

j=1,2,…,M

(10)

bk=bk+ekk=1,2,…，L

(11)

(6)返回至步骤(2)，一直训练至误差达到所设置的理想误差为止。

2　粒子群优化算法及其改进算法

2.1　粒子群优化算法原理

粒子群优化算法最初是由美国社会心理学家Kennedy与电气工程师Eberhart观察鸟群觅食现象，受其启发于20世纪九十年代提出的。算法通过种群之间协作从而使群体达到最优。后经过Shi等人的改进，已具有很好的鲁棒性和全局搜索能力，目前成功应用于各学科领域的优化问题中，是当前进化算法的热点问题。

标准PSO算法是先初始化一群粒子，然后通过跟踪当前的最优粒子的位置和速度，得出最优解。假设在一个D维搜索空间中，有n个粒子组成种群，种群用向量表示如下X=(X1,X2,…，Xn)，第i个粒子速度和位置分别为Vi=[Vi1,Vi2,…，ViD]T，Xi=[xi1,xi2,…，xiD]T，由目标函数fitness计算出每个微粒对应的适应度值，通过每一次的迭代，找到当代个体和种群的最优解，并由式(12)和式(13)更新速度和位置：

(12)

d=1,2,…，D；i=1，2，…，n

(13)

式中：ω为惯性权重，表示微粒相信自己的程度，取值范围为[0,1],调节全局搜索和局部搜索；k为当前迭代次数；Vid为粒子第i代的速度；c1，c2为加速因子，其中c1为粒子跟踪自身历史最优的权重系数，代表粒子对自身的认识，c2为粒子跟踪群体的最优值权重系数，代表粒子对群体的认识；P为粒子位置；r1,r2为0～1之间的随机数，一般用rand()函数随机产生。

粒子群算法流程如图2所示。

图2　粒子群算法流程图

2.2　改进粒子群算法

过去几十年对影响PSO算法性能的重要参数ω，科学家提出了不同的猜想，其中Shi[8]等人采取的LDW(linearly decreasing weight)策略应用最为深远。但其存在以下问题，若在运算初期测出最优点，便希望以较快的速度收敛，随着ω的递减收敛速度下降，尤其在后期ω的减小会使全局搜索能力质量较差，易陷入局部最优情况[9]。

笔者提出了一种非线性权重PSO优化方法(improved partice swarm optimization,IPSO)，以改善上述问题，具体公式如下：

由式(14)可知，当t较小时，ω接近于ωmax，使全局搜索能力更优，随着t的增长，权重ω非线性递减，使局部搜索能力得到保证。由此，灵活地确保了全局搜索和局部搜索能力。

3　仿真分析

笔者采用数据来自本领域广泛采用的马里兰大学CALCE Battery Group研究中心的电池数据库[10]。利用CX2电池测试数据包进行数据分析处理，并对SOC进行预测，试验电池参数如表1所示。

表1　CALCE Battery Group 电池包参数

充电试验时，以0.5 C的放电倍率恒流充电至电压达到4.2 V，然后恒压充电，一直到充电电流至0.05 A时充电截止。放电试验时，以0.5 C的放电倍率恒流放电至截止SOC状态。

选取200组数据作为训练样本，包含电压、电流、温度三个训练样本输入，SOC作为训练样本输出，另25组数据作为测试数据，以验证算法的可靠性。部分训练数据如表2所示。

表2　训练数据

3.1　BP神经网络仿真结果

BP神经网络输入层，隐含层，输出层各网络节点分别为3,7,1。初始化参数如下：最大训练次数为1 000；学习速率为0.01；目标误差为1e-4。得到BP神经网络预测SOC值以及误差值，如图3和图4所示。

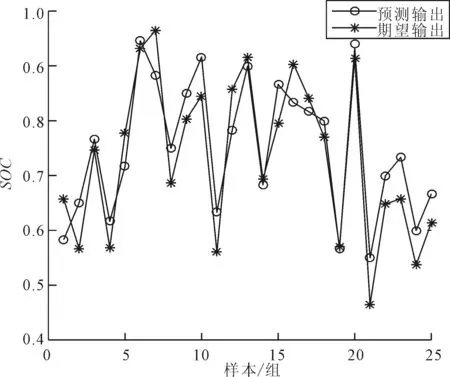
图3　BP神经网络预测SOC值

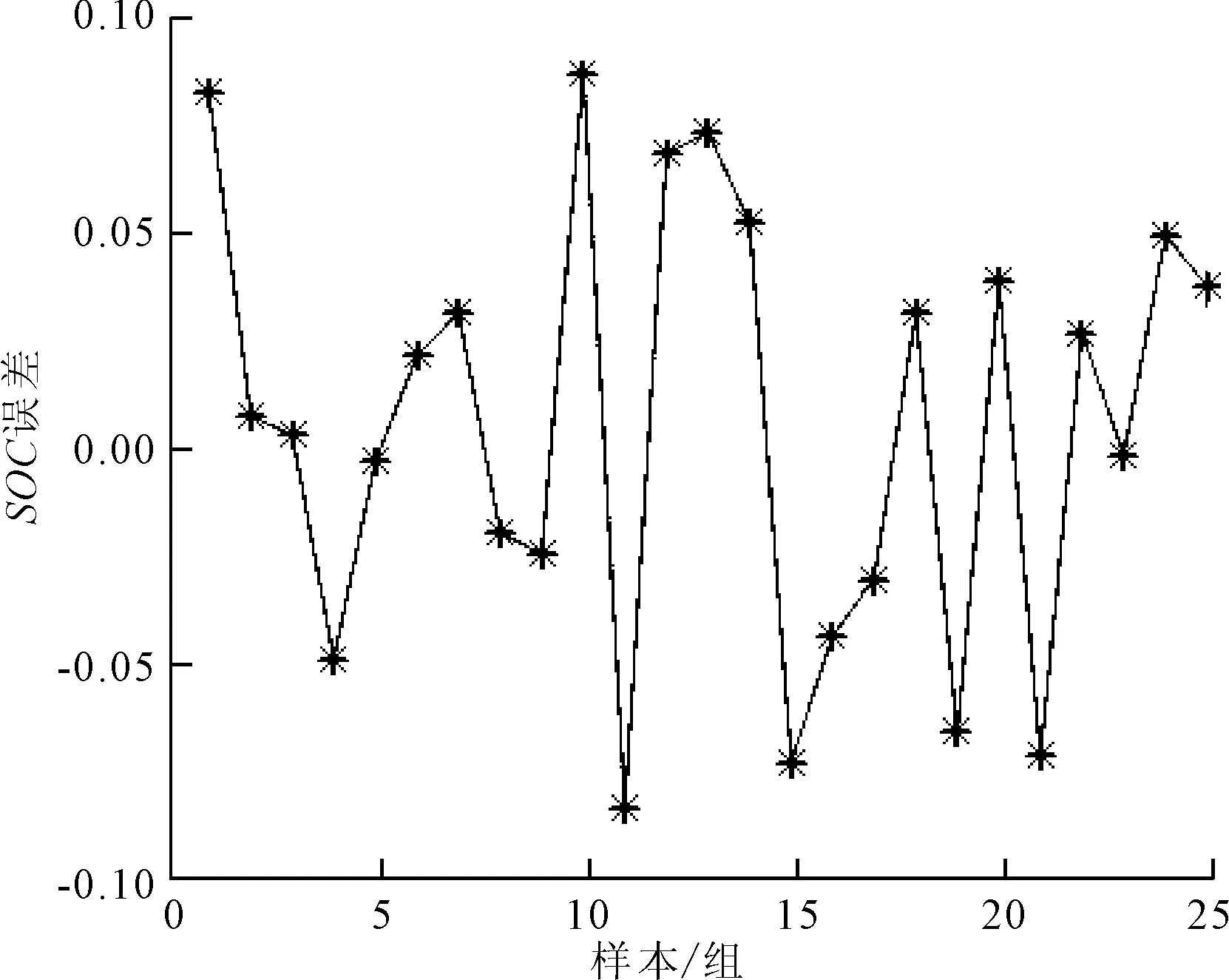
图4　BP神经网络预测SOC误差

由图3和图4可知，BP神经网络预测SOC的结果误差波动范围大，权值和阈值对网络训练影响很大，因此笔者针对阈值和权值利用IPSO-BP进行优化。

3.2　IPSO-BP神经网络预测结果

基于粒子群算法优化的BP神经网络预测的收敛性适中，设置种群规模为40，迭代次数为1 000，学习因子c1，c2之和通常接近4，选择c1≈c2≈2.05，预测SOC值及误差结果如图5～图6所示。

图5　IPSO- BP神经网络预测SOC值

图6　IPSO-BP神经网络预测SOC误差

4　仿真结果分析及误差比较

图7　三种算法预测SOC误差比较

使用CALCE Battery Group同一测试样本，不同算法的预测误差相差较大。三种算法预测SOC误差如图7所示。试验误差越趋近于误差基线，代表算法更优，适用性更好。由图3和图5可知，BP的拟合程度较差，期望输出和网络预测输出间隔较远，IPSO-BP则表现出很好的精度，期望输出和预测输出基本吻合。由图4、图6、图7可知，BP神经网络预测误差较大，波动范围在1%～10%之间，精度不高，收敛性不强。GA优化BP神经网络误差相对较小，所选测试样本中，波动范围在0～4%之间，可以满足需求精度不高的SOC预测。IPSO优化BP神经网络预测输出和测试样本输出重合度最高，误差的波动范围最小，在0～2%范围内，可满足SOC预测精度有较高要求的情况。由此可见，改进的PSO算法优化的BP神经网络很好地解决了BP神经网络陷入局部最优的问题，得到了很好的收敛性。对于GA优化的BP神经网络，由图7可以看出，虽然个别误差值和IPSO-BP预测误差值相近，但从总体水平上看，IPSO-BP算法的绝对误差更贴近基准线，IPSO-BP在预测精度方面是更胜一筹，在具体的工程实际中有很好的适用性。

5　结论

笔者提出了基于数据驱动的SOC预测方法，BP神经网络结构简单，易于操作，泛化能力强，因此采用它进行预测，但BP易陷入局部最优，权值和阈值的选择导致误差偏大，笔者基于CALCE Battery Group的实验数据，分别建立GA-BP和IPSO-BP模型，优化BP的权值和阈值，得到较好的效果，其中IPSO-BP模型误差更小，基本满足现代汽车中对电池剩余容量的预测要求。

参考文献：

[1]姜琳．锂离子电池荷电状态估计与寿命预测技术研究[D].成都：电子科技大学，2013．

[2]尹安东，张万兴，赵韩，等．基于神经网络的磷酸铁锂电池SOC预测研究[J].电子测量与仪器学报，2011，25(5):433-437．

[3]林成涛，王军平，陈全世．电动汽车SOC估计方法原理与应用[J].电池，2004，34(5):376-378．

[4]雷晶晶，李秋红．动力锂离子电池管理系统研究进展[J].电源技术，2010，34(11):1192-1195．

[5]张利，朱雅俊，刘征宇．锂离子电池 SOC 与模型参数联合估算研究[J].电子测量与仪器学报，2012，26(4):320-324．

[6]陶海龙，李小平，张胜召,等.基于IPSO-BP神经网络的铁路客运量预测[J].铁道运输与经济，2011，33(9):78-82.

[7]Eberhart R , Kennedy J. A New Optimizer Using Particle Swarm Theory[C]∥Proceeding of the Sixth International Symposium on Micromachine and Human Science.Piscataway: IEEE Service Center，1995:42-46.

[8]Shi Y, Eberhart R C. A Modified Particle Swarm Optimization[C]∥Proceedings of the IEEE Congress on Evolutionary Computation. Piscataway: IEEE Presss，1998:62-66.

[9]魏秀业，潘宏侠.群优化及智能故障诊断[M].北京：国防工业出版社，2010.

[10]Fangdan Zheng, Yinjiao Xing. Influence of Different Open Circuit Voltage Tests on State of Charge Online Estimation for Lithium-ion Batteries[J].Applied Energy, 2016,183:513-525.