降水量空间插值方法在小样本区域的比较研究
解恒燕, 张深远, 侯善策, 郑 鑫
(黑龙江八一农垦大学 工程学院, 黑龙江 大庆 163319)
目前,气候及环境的变化严重影响了区域降水分布规律,导致了区域性旱灾涝灾频繁发生[1-2],因此,掌握多年的区域降水分布规律具有重要意义。如潘旸等将最优插值方法对地面观测与卫星反演降水二者进行融合,开发出一套高时空分辨率和高精度的降水分析产品,预测降水分布规律[3]。通常研究降水分布规律需要多年且可靠的降水量数据为依据,同时降水量数据是水资源管理与分析、水文模型应用的基础数据[4-5]。降水量数据通过气象观测点获得,但对无气象观测点、无降水量数据或有气象观测点缺失降水量数据的情况,需要对降水量数据进行估值。关于降水量数据估值研究比较多,如熊敏诠应用Delaunay三角剖分法对降水量进行估值,对比分析了三角分片线性插值和反距离权重法的估值准确率[6]。插值方法是解决降水量数据缺失问题常用方式之一。
空间插值方法是采用区域内已知观测数据来获取未知数据。李莎等利用时空克里金插值方法对黑龙江省月均气温进行估计,证明时空克里金法效果最好[7]。金君使用多种插值方法,采用187个气象站49 a气温及降水量的年平均值进行空间插值,插值结果表明,梯度距离平方反比法对年平均气温值的插值精度最高[8]。林金煌等基于ArcGIS 10.1平台,采用了3种常用插值方法对福建省降水量进行空间插值[9]。李丽双等应用多种空间插值方法对东北地区年降水量和月平均气温等气象要素进行了插值[10]。众多学者在使用降水量空间插值方法进行研究时,通常选择观测点数量较多的研究区域,而对于气象观测点少的小样本区域,相关研究成果较少,降水量空间插值方法的适用性未见系统报道。
对于某个已知的特定区域,样本数量的多少,决定这个区域属于“大样本”区域还是“小样本”区域。本文研究在不考虑其他影响因素的前提下,当样本数量逐渐减少时,某一特定区域从“大样本”区域变为“小样本”区域过程中,不同降水量空间插值方法的适用性。假设某个观测点实测数据未知,利用其他观测点实测数据计算出该点插值结果,然后将该观测点插值结果与实测数据进行比较,分析插值方法的精度。本文选取美国伊利诺伊州Upper Sangamon流域9个气象站点2002—2007年的72个月降水量数据,分别采用普通克里金法、反距离权重法、样条函数法、趋势面法进行插值及分析。为模拟小样本区域,通过减少已知观测点数量,分析应用不同插值方法时,观测点数量对插值精度的影响。
1 资料与方法
1.1 Upper Sangamon流域概况
Upper Sangamon流域位于美国中西部地区,地理位置位于北纬39.8°—40.5°,西经88.1°—89.5°,属于平原地区,地势平缓,降水量受地形因素影响较弱,纬度接近我国黄河以北地区,该流域降水量分析及结论对我国部分流域具有一定参考价值。Upper Sangamon流域气象观测点分布见图1。由图1可见,该流域气象观测点分布较合理,因此可以对该流域气象站点降水量观测数据进行定量分析。本文数据来源于美国国家气候数据中心(National Climatic Data Center,NCDC)官网,其观测数据为NCDC官网提供的2002—2007年Upper Sangamon流域9个气象站点的日实测降水量,累计求和,计算得到月降水量。经统计分析,利用显著性水平α=0.05的χ2拟合优度检验了降水量分布情况,该流域月降水量符合极值Ⅰ型分布[ 11-13]。

图1UpperSangamon流域高程及气象站点分布
1.2 空间插值方法
1.2.1普通克里金法普通克里金法以区域变化量理论为基础,利用半变异函数得到最佳权重系数,进而求得最优估计值[14]。该方法的优点是考虑了样本点在空间结构中随机分布的特点。估计值的精度取决于权重系数的选择,最佳权重系数取决于变异函数模型的选择,本文利用该方法时选择了球形函数模型。普通克里金法计算公式为:
(1)
式中:Z(x0)为待估点x0的待估值;n为样本点的数量;λi为权重系数,判断已知点数据Z(xi)对待估点数据的贡献;x为数据已知点的位置;x0为待估点的位置。
1.2.2反距离权重法反距离权重法是将数据已知点与待估点的距离进行加权平均,得到待估点的估计值[15]。该方法根据相近相似的原理,当空间中两个点位置距离越远,它们的空间差异性就越大;反之,距离越近则空间差异性越小[16-17]。反距离权重法计算公式与式(1)相同,该方法与普通克里金法主要区别是权重系数求解过程不同,采用点间距离倒数反比法求得,其权重系数计算公式为:
(2)
式中:p为指数值,一般为2;di为待估点到第i点距离。
1.2.3样条函数法样条函数法是通过多项式拟合样本点数据来产生平滑插值曲线的插值方法。该方法的优点是保留了局部地形的细部特征,获得连续光滑的拟合曲面,具有较好的保凸性、逼真性和平滑性[18]。本文采用基于ArcGIS的规则样条函数法进行插值,该方法计算公式为:
(3)
式中:Z为待估点的估计值;n为样本点数量;λi为线性方程组求解确定的系数;di为待估点到第i点距离;x、y分别为平面直角坐标系中横、纵坐标数值;R(di)是以di为自变量的方程式;T(x,y)是以x、y为自变量线性方程组;R(di)与T(x,y)的公式见参考文献[19]。
1.2.4趋势面法趋势面法是采用多项式回归方法得到适合地理要素空间分布规律的曲面平滑程度,再根据该曲面方程计算待估点的属性值[20-22]。趋势面法的计算公式为:
(4)
式中:Z(x,y)为待估点的估计值;n0为多项式阶数;ε为趋势面和真实面存在一个随机误差;ak,j为观测点的观测值确定系数;x、y分别为平面直角坐标系中横、纵坐标数值。
1.3 插值精度评价方法
插值精度主要评价指标是平均相对误差(Mean Relative Error,MRE)[23-24]。平均相对误差反映误差绝对值相对于观测数据的大小,其计算公式如式(5)所示,该指标数值越小插值精度越高。
(5)
式中:Yi为插值结果;Xi为观测数据;n为估计点个数。
2 插值结果与分析
对Upper Sangamon流域的内插点及外推点两类站点进行插值。当待估点位于已知观测点的区域内时,该估算过程称为内插,待估点为内插点;当待估点位于已知观测点的区域外时,该估算过程称为外推,待估点为外推点。根据这一定义,Upper Sangamon流域内区域中间的CISCO(CIS)、DECATUR AIRPORT(DEC-A)、MONTICELLO RIVER(MON-R)、MAHOMET(MAH)、FISHER(FIS)站点为内插点,区域边缘的GIBSON CITY(GIB-C)、RANTAOUL(RAN)、DECATUR WTP(DEC-W)、BUFFALO(BUF)站点为外推点。
2.1 不同插值方法降水量插值精度比较分析
分别应用反距离权重法、普通克里金法、样条函数法及趋势面法4种空间插值方法,对Upper Sangamon流域中9个站点的降水量数据分别进行了插值,平均相对误差见图2。横坐标中前5个站点为内插点,后4个站点为外推点。
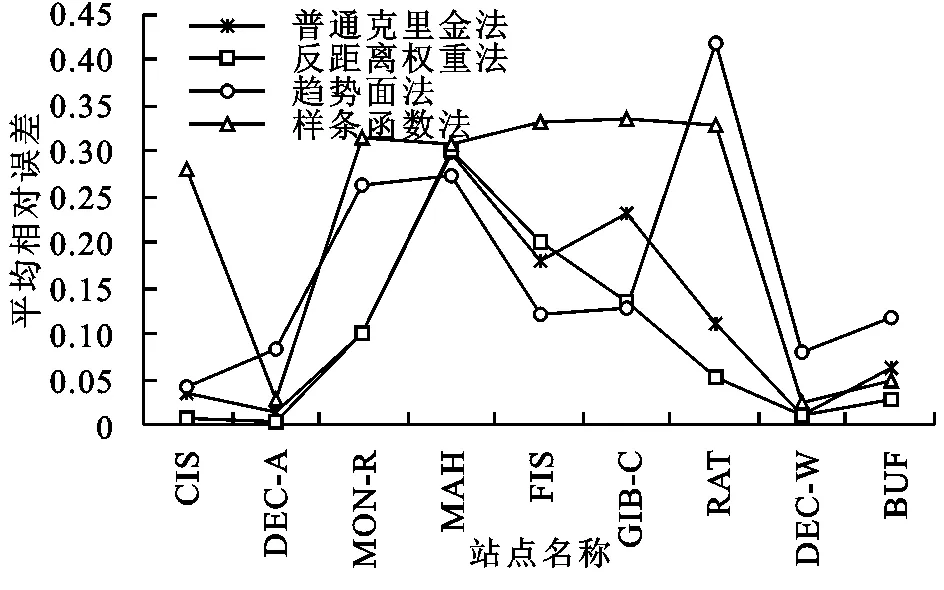
图2 降水量估计值平均相对误差
由图2可知,5个内插点中,CISCO,DECATUR AIRPORT站点反距离权重法得到平均相对误差小于其他3种插值方法,MAHOMET,FISHER站点趋势面法得到平均相对误差小于其他3种插值方法,MONTICELLO RIVER站点反距离权重法与普通克里金法得到平均相对误差基本一致,并优于其他两种插值方法。4个外推点中,RANTAOUL,DECATUR WTP,BUFFALO站点反距离权重法得到平均相对误差小于其他3种插值方法,GIBSON CITY站点趋势面法得到平均相对误差小于其他3种插值方法,但与反距离权重法得到平均相对误差非常接近。因此,对于小样本区域,4种降水量空间插值方法中,反距离权重法插值精度明显优于其他3种空间插值方法。
2.2 不同观测点数目的降水量插值精度比较分析
为研究观测点数目对降水量空间插值精度的影响,以距待估点距离为依据,按照由远及近的顺序减少已知观测点的数量,将已知观测点个数分别定为8个、5个及3个。本文计算的最少观测点个数是3,当区域样本数量低于3时,插值方法意义不大。分别计算9个站点在3种不同观测点数目情况下,应用反距离权重法进行降水量插值计算,平均相对误差见图3。

图3 降水量估计值平均相对误差(反距离权重法)
由图3可知,5个内插点中,CISCO,DECATUR AIRPORT,MONTICELLO RIVER,FISHER站点在3种情况下得到平均相对误差很接近,在MAHOMET站点8个观测点情况下得到平均相对误差小于其他两种情况,但三者相差不大。4个外推点中,GIBSON CITY,RANTAOUL站点在3个观测点情况下得到平均相对误差均小于5个、8个观测点情况,DECATUR WTP站点在5个观测点情况下得到平均相对误差小于3个、8个观测点情况,但三者得到平均相对误差很接近,BUFFALO站点在8个观测点情况下得到平均相对误差小于3个、5个观测点情况,但三者得到平均相对误差均小于0.5。因此,利用3个观测点对外推点进行插值能够满足实际需要的。观测点数量对反距离权重法插值结果影响不大。
应用普通克里金法进行降水量插值计算,平均相对误差见图4。

图4 降水量估计值平均相对误差(普通克里金法)
通过比较图3,图4可知,CISCO,MONTICELLO RIVER,MAHOMET站点两图在8个观测点得到平均相对误差较低,GIBSON CITY,RANTAOUL站点在3个观测点得到平均相对误差较低,FISHER,DECATUR WTP站点在5个观测点得到平均相对误差较低,DECATUR AIRPORT,BUFFALO站点得到较低平均相对误差的观测点数目不一致,但三者得到平均相对误差都接近0.5或者低于0.5。图中折线变化趋势有着相似特征,两种方法对9个站点降水量插值结果的变化趋势比较接近。
应用样条函数法、趋势面法进行降水量插值计算,两种方法的平均相对误差分别见图5,图6。
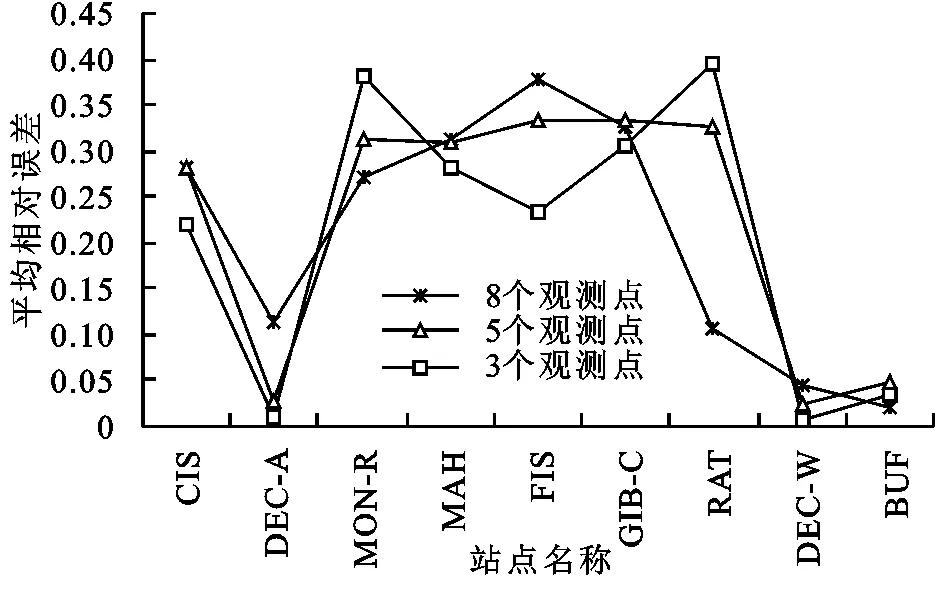
图5 降水量估计值平均相对误差(样条函数法)
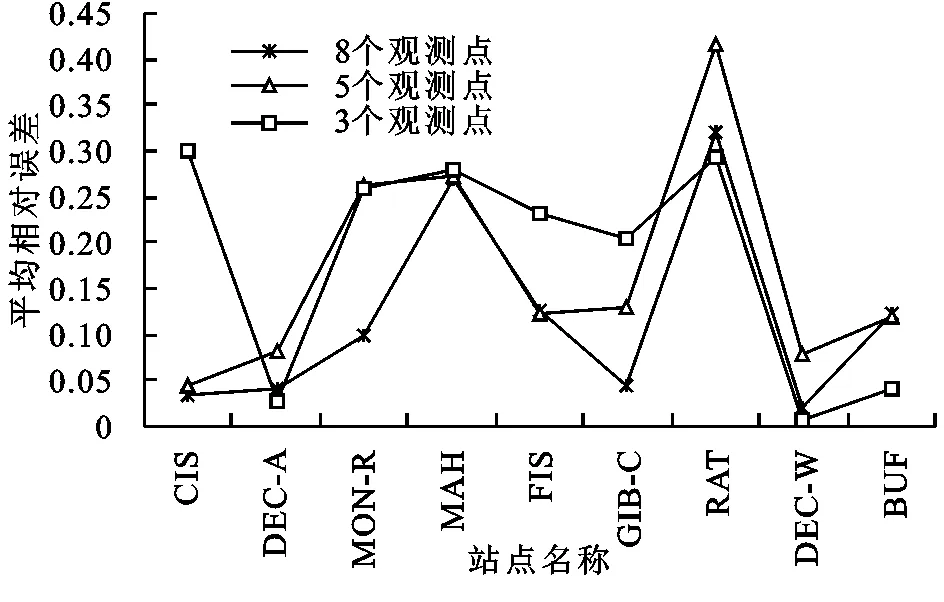
图6 降水量估计值平均相对误差(趋势面法)
将图3、图4与图5、图6进行比较可知,观测点数目变化时,图5、图6中三者之间的平均相对误差之差变化范围大约0.1~0.3,平均相对误差变化幅度较大,而图3中三者之间的平均相对误差之差变化范围小于或接近0.05,图4中三者之间的平均相对误差之差变化范围小于或接近0.1,平均相对误差变化幅度较小。因此,观测点数量对样条函数法与趋势面法影响高于其他两种方法,而普通克里金法受影响程度又大于反距离权重法。
3 讨 论
本文针对观测点数量较少的小样本区域进行研究,仅考虑了站点间距离的因素。反距离权重法模型建立主要参数为距离,而本文研究中选择观测点考虑的参数与反距离权重法模型建立参数是相同的,使该方法在每一个观测点插值结果较为理想,而观测点数量变化对其影响也不大。如果选择观测点考虑的参数与其他3种空间插值方法模型建立主要参数相接近,或者选择观测点方式考虑到了空间插值方法模型建立核心概念,那么其他3种空间插值方法是否可以通过较少的观测点数量得到较优的插值结果,即受观测点数量变化影响也会较小,这些问题需要进一步研究探讨。同时,应用空间插值方法对降水量数据插值,如何在已知观测点数量少且排除影响降水量因素(如经纬度、风向、高程、地形以及大气环境)的情况下,使降水量数据插值结果更优,仍需要不断地探索与研究。
4 结 论
(1) 待估点位置不同影响着空间插值方法的插值精度。在外推点上,反距离权重法插值精度明显优于其他3种空间插值方法;在内插点上,反距离权重法较优于其他3种空间插值方法。
(2) 空间插值方法插值精度随着观测点数量变化而变化,对于按照距待估点距离由远及近减少观测点的选点方法,反距离权重法插值精度较高,无论是外推点还是内插点,反距离权重法受观测点数量影响最小,其可利用3个观测点就能够得到满足实际需要的数据。普通克里金法受观测点数量影响程度次于反距离权重法,但两种方法对9个站点降水量插值结果的变化趋势比较接近。样条函数法与趋势面法受观测点数量影响较为严重。
参考文献:
[1]张强,韩兰英,郝小翠,等.气候变化对中国农业旱灾损失率的影响及其南北区域差异性[J].气象学报,2015,73(6):1092-1103.
[2]宇如聪,李建,陈昊明,等.中国大陆降水日变化研究进展[J].气象学报,2014,72(5):948-968.
[3]潘旸,沈艳,宇婧婧,等.基于最优插值方法分析的中国区域地面观测与卫星反演逐时降水融合试验[J].气象学报,2012,70(6):1381-1389.
[4]李朝奎,陈良,王勇.降雨量分布的空间插值方法研究:以美国爱达荷州为例[J].矿产与地质,2007,21(6):684-687.
[5]何艳虎,林凯荣.降雨空间插值方法在东江流域的比较运用[J].水力发电,2010,36(10):7-9.
[6]熊敏诠. Delaunay三角剖分法在降水量插值中的应用[J].气象学报,2012,70(6):1390-1400.
[7]李莎,舒红,徐正全.利用时空Kriging进行气温插值研究[J].武汉大学学报:信息科学版,2012,37(2):237-241.
[8]金君,彭思岭,刘启亮,等.中国陆地区域气象要素空间插值方法比较研究[J].工程勘察,2010,38(11):48-51.
[9]林金煌,林广发.福建省降水空间插值方法比较与区域分布特征研究[J].海南师范大学学报:自然科学版,2015,28(1):61-65.
[10]李丽双,张颖.基于GIS的东北地区气象要素空间插值方法[J].安徽农业科学,2012,40(9):5541-5543.
[11]尹文有,郑皎,王继红,等.年最大日雨量极值分布拟合与推算[J].气象科技,2011,39(2):137-140.
[12]郭凌曜,李英.湖南省短历时降水极值分布拟合与应用[J].气象与环境学报,2015,31(3):69-74.
[13]司波,余锦华,丁裕国.四川盆地短时强降水极值分布的研究[J].气象科技,2012,32(4):403-410.
[14]刘昌明,郑红星,王中根.流域水循环分布式模拟[M].郑州:黄河水利出版社,2006.
[15]Zoubeida K B, Afef C. Comparison of two kriging interpolation meth-ods applied to spatiotemporal rainfall[J]. Journal of Hydrology, 2009,365(2):56-73.
[16]黄开勇,唐咸艳,王晓敏,等.桂林市道路交通伤害GIS反距离加权插值法分析[J].中国公共卫生,2012,28(5):576-577.
[17]董晓华,薄会娟,邓霞,等.降雨空间插值方法及在清江流域的应用[J].三峡大学学报,2009,31(6):6-10.
[18]李军,游松财,黄敬峰.中国1961—2000年月平均气温空间插值方法与空间分布[J].生态环境,2006,15(1):109-114.
[19]李巍,范文义,毛学刚,等.降雨量空间插值方法比较研究[J].安徽农业科学,2014(12):3667-3669.
[20]王勇,李朝奎,陈良,等.权重对空间插值方法的影响分析[J].湖南科技大学学报:自然科学版,2008,23(4):77-80.
[21]孙然好,刘清丽,陈利顶.基于地统计学方法的降水空间插值研究[J].水文,2010,30(1):14-30.
[22]彭思岭.气象要素时空插值方法研究[D].长沙:中南大学,2010.
[23]Daly C. Guide lines for assessing the suitability of spatial climate data set[J]. International Journal of Climatology, 2006,26(5):707-721.
[24]何文英,毕孟飞,李泽利,等.新安江流域降雨量空间插值方法和参数筛选[J].水资源与水工程学报,2013,24(1):130-134.

