贝叶斯层次时空模型在省际人口流入分析中的应用
李 原
(山西财经大学 统计学院,太原 030006)
0 引言
上世纪80年代以来,我国人口流动规模越来越大。“六普”数据显示,2010年中国大陆流动人口已超2.6亿人,占总人口的16%以上,国家统计局调查数据显示,2015年流动人口达2.92亿。大规模的人口流动直接影响区域人口规模结构和经济格局,进而影响全国经济发展的结构变迁、产业升级和人口城镇化进程,有关人口流动的研究在我国变得越来越重要。
围绕我国人口流动模式问题,国内很多学者进行了相关探讨,相关文献的定量研究方法可分为三类:人口迁移指标的描述统计分析法、多元回归模型分析法及空间计量分析法。已有研究大都基于普查数据采用经典统计方法分析我国人口流动问题。经典统计视未知参数为固定常数,基于大样本对总体进行推断,估计结果高度依赖样本信息,遇到有偏样本则会导致参数估计结果有偏,特别是对于人口流动空间数据而言,其同时具有小样本和自相关的特性,基于大样本推断总体的传统统计模型由于自身的局限受到更多挑战。
而贝叶斯层次时空模型是贝叶斯层次模型和时空交互模型的结合,贝叶斯层次模型可在一定程度上克服小样本缺陷,时空交互模型同时考虑空间相关和随机效应,贝叶斯层次时空模型为时空数据统计分析提供了全新的思路和方法,应用该模型进行人口流动分析,能解决经典统计难以解决的问题,同时能克服以往人口流动分析对时间和空间交互作用的忽略。
实际上,贝叶斯层次时空分析法近年在国际上受到广泛的重视,特别是在生态学、疾病传播等方面的理论和方法探索越来越多,目前国内也出现了相关的应用,但该方法在人口流动特征分析中的应用还未见。本文首次应用贝叶斯层次时空模型,对我国2009—2014年间省际人口流入的时空演化特征进行分析。
1 Bayesian层次时空模型
贝叶斯层次时空模型是贝叶斯层次模型和时空交互模型的结合,贝叶斯层次模型主要包括三个子模型:

θj为参数,φ是超参数,P(φ)是超先验。P(θj,φ|yi)是参数和超参数的后验分布,参数和超参数的后验分布可通过似然函数、先验分布和超先验分布的乘积获得:
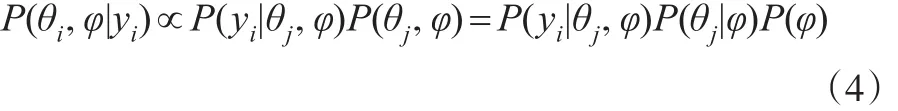
后验分布的计算涉及高维联合概率密度函数估计,目前主要采用马尔科夫链-蒙特卡洛法实现。为保证模型收敛性,可采用两条MCMC链,收敛性通过Gelman-Rubin统计参数估计,其值越接近于1收敛性越好。
空间自相关性是空间数据的一大特点,不满足独立同分布特征,样本数据有限时难以达到大样本抽样。而贝叶斯层次时空模型是贝叶斯层次模型与时空交互模型的结合,可以克服上述缺陷,该模型通过充分利用先验信息,考虑时空交互项,同时考虑了数据的空间自相关性和随机不确定性,以概率分布的形式描述时空特征,相应的三个子模型为:
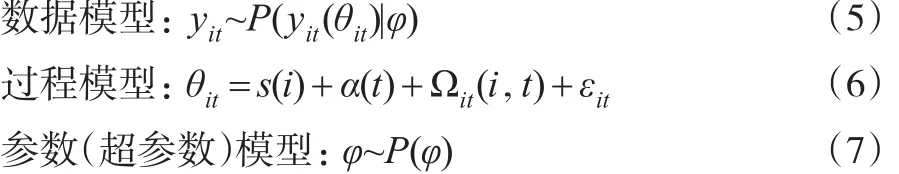
yit是时空观测样本值,θit是时空因变量,s(i)和α(t)分别代表稳态空间相对风险和总体变化趋势,Ωit(i,t)为时空交互项,该项常用的表达形式为,代表研究时段内各研究子区域的局部变化趋势,bi度量从总体变化趋势中分解出的局部变化程度,若bi>0,说明其局部变化强度强于总体变化强度,bi<0说明其局部变化强度弱于总体变化强度,t*=t-tm表示相对于研究期内中间时点tm的时间跨度。εit是随机噪声。
计算所有参数后验分布后,可根据各区域时空因变量的空间相对风险s(i)的高低将其分为热点、温点和冷点区。该分类方法基于Richardson等(2004)提出的原则:若地区空间相对风险大于1的后验概率大于0.8,则属于热点区,若小于0.2则属于冷点区,界于0.2和0.8之间为温点区。与此类似,根据各区域观测值局部变化趋势bi可将其分为强变化、稳定态和弱变化三种局部趋势状态。若局部趋势参数bi>0的后验概率大于0.8,p(bi>0)>0.8,则为强变化区,若p(bi>0)<0.2则为弱变化区域,其余为稳态区。
评价贝叶斯时空分解的稳定组分对整个时空变化过程的解释度,常用指标是方差成分系数(VPC),VPC越大,则时空组分分解对时空变化过程的解释度越高,表达式为:
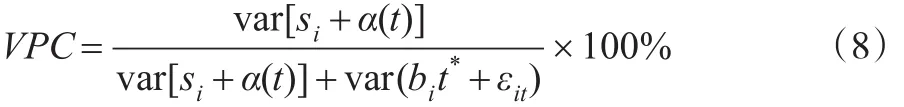
2 实证分析
2.1 数据与指标
本文研究区域范围为中国大陆31个省级行政区域,由于普查数据滞后性太大,因此选用时效性较好的《中国人口和就业统计年鉴》数据,该年鉴可提供2009—2014年统计口径一致的省际人口迁入率指标,该指标是某地区某时期的迁入人口占该地区同时期总人口的比重,迁入人口指住本乡、镇、街道,户口在本乡、镇、街道,离开户口登记地半年以上的人口。
2.2 描述统计分析
总的来看,2009—2014年我国各地区人口迁入率有大幅度上升,2009年,我国总平均迁入率为8.6%(表1),2011年达到19.5%后开始缓慢下降,2014年总平均迁入率达19%。2009年只有北京、上海、广东、福建、浙江、天津、江苏、内蒙8个地区人口迁入率大于10%,2014年只有西藏、江西、甘肃、河南和河北5个地区人口迁入率低于10%。

表1 2009—2014年全国各地区人口迁入率统计值 (单位:%)
2009—2014年,我国各地区人口流入的格局大致稳定,上海和北京一直是我国人口流入最高的两大地区,具有对人口迁入的巨大吸引力。其次是浙江、福建和广东,东部沿海地区的快速发展吸引了大量人口,三个地区的人口迁入率2010年后都达到30%以上,特别是浙江和福建,几乎达到了40%。迁入率偏低的地区有西藏、甘肃、河北、河南、江西和云南,主要分布在中西部地区,这些地区2009年和2010年,人口迁入率都不到5%,2014年都不到10%,特别是西藏,一直是我国人口迁入率最低的地区。
2.3 中国省际人口流入贝叶斯时空模型设定与检验
迁入人口观测数据属于计数数据,且个人迁入概率不完全相同,存在过度散布情形,因此数据模型采用泊松-伽马混合模型:

其中,yit表示i(i=1, 2,..., 31)地区t年时迁入人口数,λit表示i地区t年时的迁入人口均值,uit是i地区t年时的随机效应参数,rit是散度系数,相应的概率密度函数为:
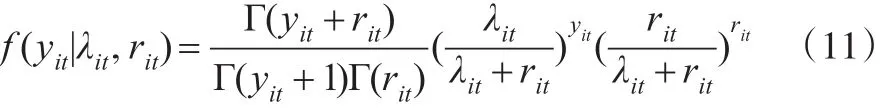
过程模型为:

pit为i地区t年迁入率,α为全国总体省际人口迁入基础常数,si为i地区人口迁入的空间相对风险参数,βt*+vt描述全国人口迁入率时间变化趋势,bit*为各地区的局部变化趋势,bi度量从总体变化趋势中分解出的局部变化程度,若大于零说明其局部变化强度强于总体变化趋势,若小于零说明局部变化强度弱于总体变化强度,εit是高斯噪声随机变量。
参数si和bi的先验分布用Besag York Mollie(BYM)模型确定,BYM模型通过卷积运算实现空间结构和非结构随机效应的相互作用,数学表达式为:

l(y|θ,Θ)为样本似然函数,Sit表示时空域,利用条件自回归先验分布表示空间结构随机效应,空间邻接矩阵W
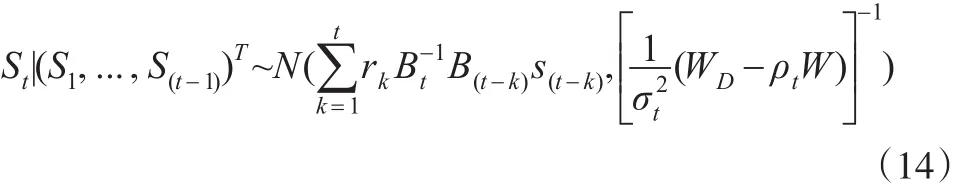
采用一阶“皇后”邻接形式,其先验分布形式为:St是时空随机变量,rk和ρt分别代表时间和空间相关性参数,,I是单位矩阵,σt是t时期的总体方差,上述先验分布对应的概率密度函数为:
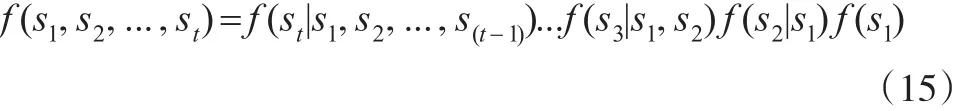
本文模型估计通过实现贝叶斯层次模型的专门软件WinBUGS完成。为保证模型运行的收敛性,采用了两条MCMC链,每条链的迭代次数均设置为20万次,所有参数的Gelman-Rubin统计值都低于1.005,说明该模型收敛性较好。
2.4 中国省际人口流入贝叶斯时空模型统计分析结果
2.4.1 空间相对风险和总体时间趋势估计结果
根据各地区人口迁入率的空间相对风险大于1的后验概率把各地区分为热点、温点和冷点区域(见表2)。在研究期内,人口迁入率高于全国总体水平的热点区域有7个(按相对风险中值估计值降序排序):上海(3.15)、北京(2.77)、浙江(1.86)、福建(1.74)、天津(1.49)、广东(1.48)、江苏(1.34),主要集中在京津地区和东部沿海地区;温点区域有11个(按相对风险中值估计降序排序):内蒙(1.28)、宁夏(1.24)、辽宁(1.13)、海南(1.13)、山西(1.00)、黑龙江(1)、吉林(0.98)、新疆(0.97)、重庆(0.95)、青海(0.88)、河北(0.83),温点区域主要集中在东北地区,包含华北地区和西北地区部分省份。冷点区域有13个(按相对风险中值估计降序排序):江西(0.97)、湖北(0.86)、安徽(0.84)、贵州(0.84)、陕西(0.83)、四川(0.82)、广西(0.78)、云南(0.77)、山东(0.75)、甘肃(0.69)、湖南(0.68)、河南(0.64)、西藏(0.63),除山东省外,冷点区域都集中于我国中西部地区。冷、热、温点区域具体地理分布见下页图1。从图1可见,我国人口迁入的冷、热、温点各自集中分布特征明显,冷点区覆盖了我国中西部的大部分区域。温点地区除重庆市被冷点区环绕外,整个东北地区和华北地区的内蒙、山西与河北以及宁夏接壤成片,面积广袤的新疆和青海紧密相连,形成我国地区人口流入的温点区。热点区除京津两地外大都集中于东南沿海地区,形成地区人口流入的环带状热点区域群。
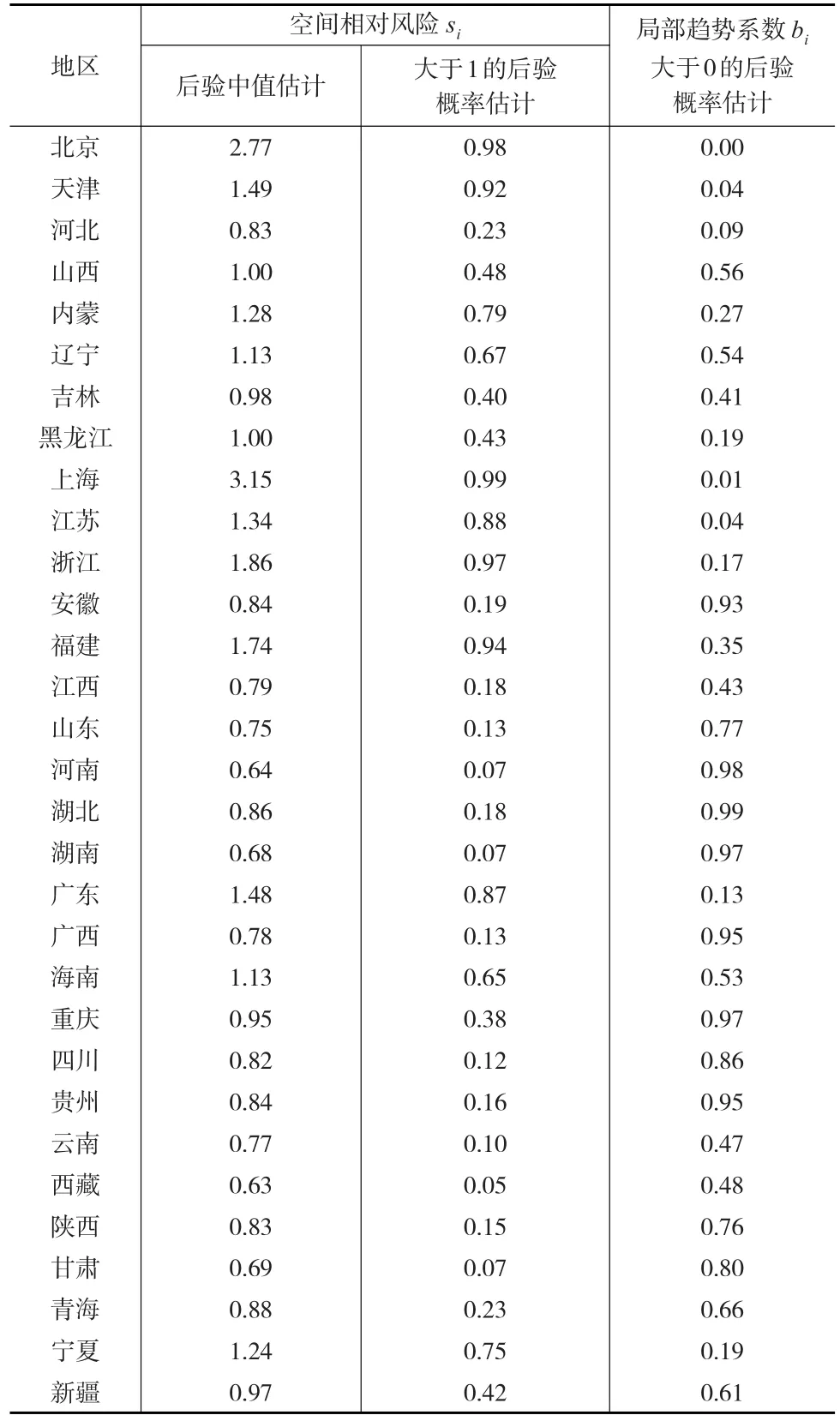
表2 全国各地区人口迁入总体相对风险和局部趋势估计结果
不可置否,地区人口迁入与地区经济发达程度密切相关,2014年人均GDP排在前9位的地区依次为天津、北京、上海、江苏、浙江、内蒙、辽宁、福建和广东,除内蒙和辽宁外,其余7省(市)都属于人口迁入的热点区域,人口迁入的热点区也是地区经济的发达区;13个人口迁入的冷点区域有9个区域(湖北、湖南、陕西、山东除外)人均GDP的排名位于最末10位,人口迁入的冷点区域也是地区经济欠发达区域;11个温点区域其GDP排名除内蒙和辽宁较靠前、山西较靠后外,其余9个温点区域在全国的位次排在11位至21位之间。地区人口迁入的冷热图谱与地区经济发达程度图谱高度一致。

图1 各地区人口迁入热点、温点和冷点分布图

图2 人口迁入率总体时间变化曲线(95%置信区间)
全国省际人口迁入总体变化趋势(图2)表现为曲折上升,局部表现为先上升后下降,2009—2011年表现为较快的上升,2011—2014年呈现逐年缓慢下降的态势。全国总体人口迁入率的局部走势与我国整体经济走势基本一致,2009—2014年,我国经济增长率依次为9.2%、10.6%、9.5%、7.7%、7.7%和7.3%,2009—2010年表现为上升趋势,2010—2014表现出逐年下降趋势,省际人口流入对经济放缓的响应具有一定的时滞,所以人口流入下降趋势的出现比经济增长的下降延迟了一年。
本文模型估算结果的方差成分系数VPC等于94%,说明该模型的时空分解组分对整个时空变化过程的解释度比较高,但局部变化趋势也在起作用,地区人口流入的局部变化趋势影响着全国省际人口流入的空间相对关系。2.4.2 局部变化趋势估计结果
考察各地区局部变化系数大于0的后验概率估计(表2),根据Richardson原则把全国31个省区分为强变化区域、稳定态区域和弱变化区域三个类别。我国大部分地区为人口局部变化的稳态区,包括山西、内蒙、辽宁、吉林、福建、江西、山东、海南、云南、西藏、陕西、青海和新疆13个地区,根据模型中局部趋势的统计意义,这些地区的人口流入局部变化趋势与全国总体变化趋势相当。稳态区中只有福建是热点区,说明福建人口流入程度高于全国平均水平但人口流入的局部变化与全国水平相当。稳态区中包含山西、内蒙、辽宁、吉林、海南、青海、新疆7个温点区,这7个区域人口流入水平和人口流入的局部变化都与全国平均水平相当。稳态区中江西、山东、云南、西藏、陕西为冷点区,这5个地区人口流入水平较全国低但人口流入局部变化与全国总体变化相当。强变化区域有9个,包括安徽、河南、湖北、湖南、广西、重庆、四川、贵州和甘肃,这9个地区的人口流入局部变化趋势强于总体变化趋势,又由于总体变化趋势是上升的,所以这7个地区人口流入的增加速度高于总体平均增加速度。9个强变化区域中重庆为温点区,其他8个强变化区为冷点区。弱变化区域有北京、天津、河北、黑龙江、上海、江苏、浙江、广东、宁夏这9个地区,弱变化区中大部分为热点区,少部分为温点区,不包含冷点区,包含的热点区有6个:北京、天津、上海、江苏、浙江、广东,这些热点区虽然人口流入率高于全国平均水平,但其人口流入率上升变化小于全国水平。弱变化区中的河北、黑龙江和宁夏为温点区,3个温点区人口流入水平与全国相当,其局部变化趋势弱于全国总体变化趋势。
3 结论
本文首次应用Bayesian层次时空模型,从总体和局部两个层面分析了我国地区人口流入在空间和时间上的变化特征。目前我国各地区总体平均人口流入率已接近20%,各地区人口流入的空间相对风险和局部变化趋势存在着较大的差异,本文研究发现:第一,我国人口迁入的冷、热、温点各自集中分布特征明显,地区人口迁入的冷热图谱与地区经济发展图谱高度一致,近几年,随着我国经济增长的放缓,地区人口的迁入率在逐渐下降;第二,人口迁入的热点区有7个,主要集中在京津地区和东部沿海地区,特别是上海和北京,人口迁入率一直是全国最高的。北京、天津、上海、江苏、浙江、广东这6个热点区同时属于局部变化的弱变化区,这些地区虽然人口流入率高于全国平均水平,但其人口流入率上升变化小于全国水平。热点区中的福建属于局部变化的稳态区;第三,我国人口迁入的冷点区有13个,大都集中于中西部地区,冷点区中的安徽、河南、湖北、湖南、广西、四川、贵州和甘肃这8个地区同时属于局部强变化区,这些地区人口迁入率低于全国平均水平,但人口流入率的增长态势高于全国。江西、山东、云南、西藏、陕西这5个冷点区同时属于稳态区,冷点区中无弱变化区;第四,温点区域有11个,主要集中在东北地区,包含华北地区和西北地区部分省份。温点区中的重庆属于强变化区,说明重庆地区人口流入程度与全国平均水平相当,但人口流入率的增加速度高于全国。河北、黑龙江和宁夏这3个温点区属于弱变化区,其他7个温点区同时属于局部变化的稳态区。
贝叶斯层次时空模型是研究人口流动时空特征的有效方法。基于本文研究结果,相关的政策制定需要充分认识和掌握我国省际人口流入的空间差异和局部变化趋势的异质性。充分认识北京、天津、上海、江苏、浙江、广东这6个热点区的局部弱变化性,认识安徽、河南、湖北、湖南、广西、四川、贵州和甘肃这8个冷点区的局部强变化性,注重人口迁入冷热与经济增长快慢之间以及经济发展区域格局和人口流入区域格局之间的关联,通过协调区域经济发展引导人口流动趋于合理。
参考文献:
[1]Gelman A,Rubin D B.Inference from Iterative Simulation Using Multiple Sequences.[J].Statist.Sci,1992(7).
[2]G Li,R Haining,S Richardson,N Best.Space-time Variability in Burglary Risk:A Bayesian Spatio-temporal Modeling Approach[J].Spatial Statistics,2014,(9).
[3]Richardson S,Thomson A,Best N,Elliot P.Interpreting Posterior Relative Risk Estimates in Disease-mapping Studies.[J]Environ.Health Perspect.,2004,112(9).
[4]Goldstein H,Browne W J,Rasbash J.Partitioning variation in multilevel models.[J],Underst.Statist,2002,(1).
[5]Besag J,York J,Mollie A.Bayesian Image Restoration,with two Applications in Spatial Statistics[J].Ann.Inst.Math.Stat,1991,(43).
[6]Gelman A.Prior Distribution for Variance Parameters in Hierarchical Models[J].Bayesian Anal,2006,(1).
[7]Lunn D.J.,Thomas A,Best N,Spiegelhalter D.WinBUGS-a Bayesian Modeling Framework:Concept,Structure,and Extensibility.[J]Stat.Comput,2000,(10).
[8]文雯,文小焱,胡珊等.贝叶斯层次模型在嵌套结构调查数据中的应用研究[J].中国卫生统计,2015,32(2).

