基于X13-A-S模型的中国食品价格指数研究
王斌会,史立新
(暨南大学 管理学院经济管理实验教学中心,广州 510632)
0 引言
食品价格指数是居民消费价格指数(CPI)的重要组成部分,其波动直接影响居民生活水平和消费需求,与人们的日常生活和经济社会稳定息息相关。由于人们的消费习惯和经济波动等的影响,食品价格指数存在着显著的季节性,没有经过季节调整的食品价格指数数据往往很难掌握其波动规律。因此,通过季节调整对食品价格的预测及其规律的研究有着重要的理论价值和现实意义。
国际上目前在季节调整方面的最新成果是由西班牙银行支持、美国普查局开发的X-13-ARIMA-SEATS(简称为X13-A-S),该程序在X-12-ARIMA最新版本的基础上加入了TRAMO/SEATS季节调整程序,已广泛应用于各国央行和研究机构的经济分析过程。本文采用2001年1月至2015年9月我国食品价格指数月度定基数据,运用X13-A-S模型对其季节性波动规律进行研究,加入了我国最大的传统节日春节。并对2015年10月至2016年9月的数据进行了预测。
1 原理与方法
1.1 X13-A-S基本原理
X13-A-S方法结合了X-12-ARIMA和SEATS两种方法,在操作过程中可以选择基于季节调整的SEATS模型和基于非参数调整的X-11模型。X13-A-S季节调整方法主要包含三个阶段。①通过建立RegARIMA模型对原始序列中存在的各种离群值和历法效应作预调整,然后对经过预调整后的序列进行向前预测和向后预测来补充数据;②反复尝试运用不同长度的滤子SI对序列进行移动平均操作,从原序列中分离出各种成分(趋势循环成分、季节成分和不规则成分等);③对季节调整后的结果进行各种诊断检验。其流程如图1所示。

图1 X13-A-S季节调整流程图
RegARIMA模型是ARIMA模型与一般线性回归模型的结合。对时间序列zt建立ARIMA模型:

时间序列yt的线性回归模型:

其中yt为因变量,xit为观测变量,zt为回归误差项,满足ARIMA模型。
联立式(1)和式(2)得到RegARIMA模型:
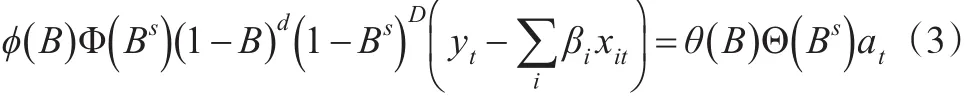
假设误差项zt差分后得到稳定序列为wt,服从稳定的ARIMA模型,则ARIMA模型简化为:

则RegARIMA模型可改写为:

RegARIMA模型不仅继承了X-11-ARIMA模型中补充首尾数据、延长时间序列的特性,还引入线性回归对观测数据的所有效应进行估计和检验。此外RegARIMA模型在X-12-ARIMA的基础上扩大异常值检验和预调整的范围,使时间序列季节调整更准确。
1.2 移动假日效应处理
移动假日是指定期出现但不一定对应着固定的公历时间的节假日。例如我国的春节、清明节、中秋节和端午节。它们都对应着固定的农历日期,但其每年所对应的公历时间却不是固定的。由于这类节假日的移动性,不能直接采用传统的移动平均方法剔除其季节性,只能考虑在季节调整的RegARIMA建模阶段引入节日回归变量的方法来剔除其季节性。根据我国的实际情况,对食品价格影响最大的移动假日是春节。春节所带来的消费高潮对食品价格指数影响显著。越接近春节,人们会更积极地为即将到来的节日做准备,置办年货的活动会越来越频繁,对食品价格指数的影响也会越来越明显,此后人们的采办活动随着春节的过去而日渐减少直到最后节日影响消除。基于以上情况,拟采用以下方案在RegARIMA建模阶段引入节日效应回归变量:把春节对我国食品价格指数的影响分为两个阶段,第一个阶段春节效应的影响每一天都是递增的,第二个阶段的影响每一天都是递减的。这两个阶段形成“∧型”。若两个阶段的长度分别为n和m,本文设节前第n天的影响权重为1/n,节前第(n-1)天的影响权重为2/n,节前第(n-2)天的影响权重为3/n。以此类推,节前第1天的影响权重为n/n;节后第1天的影响权重为m/m,节后第2天的影响权重为(m-1)/m,同样类推,节后第m天的影响权重为1/m。第i年j月所对应的影响权重就是当月的节日效应回归变量的观测值,其中不受春节效应影响的月份对应的权重为0。将计算出来的每月各天的影响权重加总后得到比例变量P(n)和P(m),然后对P(n)和P(m)分别进行中心化处理,得到春节效应的节前和节后回归变量,最后将其加入到regARIMA模型中进行估计,若对应的t检验无法通过,即表明该解释变量影响不显著,需对两个阶段的起止时期进行调整重新估计模型,不断调整直到找到最佳的模型为止。
2 数据说明
根据最新公布的CPI构成和权重,我国CPI的商品构成中食品类商品所占的比例为33.6%,其决定着CPI运行的基本趋势,本文选取我国2001年1月至2015年9月的食品价格指数为研究对象,而将2015年10月至2016年9月的数据用于预测对比,以检验模型的预测效果。数据以中华人民共和国统计局网站公布的为准。为了具有可比性,本文应选取食品价格指数的定基数据为研究对象,由于我国食品价格指数的定基数据难以获取,所以采用固定一个时期为基期,通过对每年同月的同比指数连乘来计算定基比的方法对原始序列进行调整。本文对数据的调整是以2001年为基期,假设2001年各月食品价格指数初始值为100,通过2001年1月至2016年9月的月同比食品价格指数连乘计算得到这段时期的定基指数,如图2所示。

图2 2001年1月至2016年9月我国食品价格指数定基时序图
3 模型建立
3.1 模型初设
在季节调整之前,为了避免异方差性对模型造成影响,本文首先对食品价格指数求自然对数。
日历效应设置包括:①交易日效应。即假设食品价格指数在周一至周五工作日之间存在差别,工作日与非工作日对食品价格指数波动存在影响。②闰年影响。主要表现在2月份长度对食品价格指数的影响。③移动假日效应。本文主要构建春节效应对食品价格指数的影响,考虑我国春节放假的实际情况,中国人一般习惯于从春节前10天左右开始采购年货,在春节前2天的时候达到置办年货的最高峰,之后节日的影响一直持续,直到农历正月十五元宵节后。本文将春节对食品价格指数的影响设置为“∧型”分布,第一阶段设为节前10天到节前2天,即n=8。第二阶段设为节前1天到正月十五元宵节结束,也就是m=16。第一段按照递增的方式,第二段按照递减的方式。将两阶段各天的影响权重加总后得到比例变量P(n)和P(m),中心化后得到回归变量pre_cny和post_cny,将这两个自定义变量加入回归方程进行估计。
异常值设置为选择自动识别4种常见异常值以及季节性异常值。
3.2 模型结果及检验
确定日历效应之后,建立模型,其检验结果见表1。
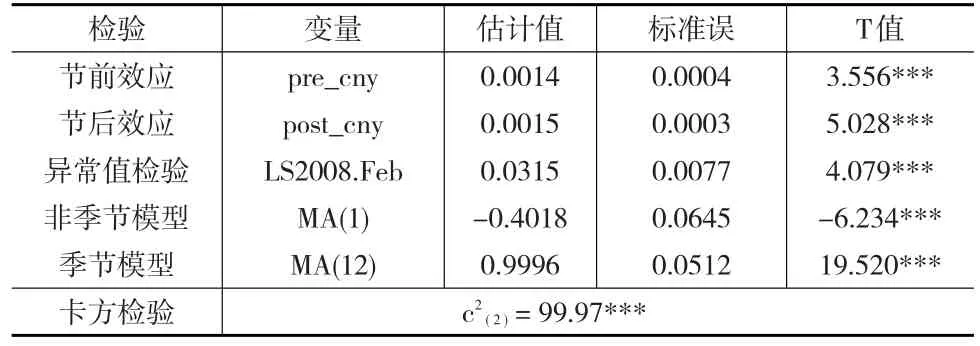
表1 我国食品价格指数季节调整模型检验结果
春节效应节前和节后估计值分别为0.0014、0.0015。由t统计量可以看出,春节效应变量pre_cny和post_cny具有很强的显著性,表明食品价格指数受春节效应影响显著,春节活动对食品价格指数有正向影响。对春节效应的两个回归因子进行卡方检验,检验两个回归因子的联合显著性。卡方检验的值为99.97,在0.1%的水平上是显著的。交易日回归和闰年效应计算表明,食品价格指数的交易日效应和闰年效应不显著。因此,在分析建模过程中没有进行交易日和闰年调整。异常值检验只检验出一个异常值,为2008年2月,异常值类型为水平移动。回归系数为正值,T值为4.079,影响十分显著。显然食品价格指数受到2008年春节期间我国南方发生的罕见雨雪冰冻灾害的影响。
接下来是建立ARIMA模型,经过识别和比较X13-A-S方法确定的模型为ARIMA(0,1,1)(0,1,1),其表示序列经过一次季节差分和一次非季节差分后,为1阶非季节移动平均项和一阶季节移动平均平稳序列。ARIMA(0,1,1)(0,1,1)的DW统计量为1.98,残差不存在自相关。
程序设计了11个M统计量和基于M的加权平均运算的Q统计量来检验季节调整的质量。M检验要求11个M统计量都小于1,Q检验则要求由11个M统计量采用不同权数组合加权得到Q值,越小越好。由表2可知,各统计量的值均小于1,因此模型质量较高。

表2 季节调整模型的M1~M11及Q统计量
我国食品价格指数的季节性检验结果如表3、表4所示:
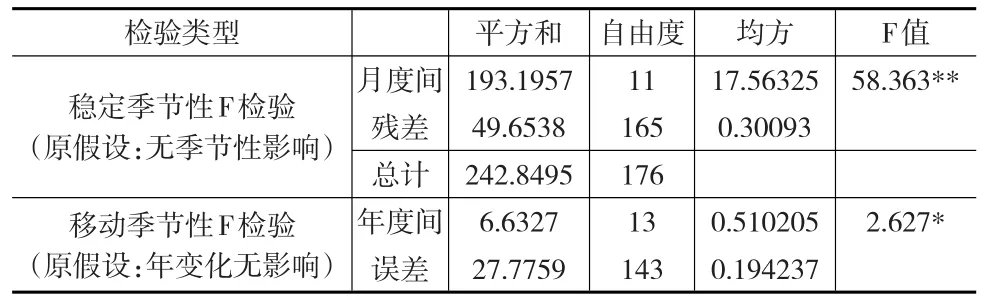
表3 食品价格指数季节性F检验

表4 食品价格指数季节性Kruskal-Wallis检验
X-11季节调整在估计季节因子时选取的是3×5季节移动滤波,在估计趋势循环因子时使用9期Henderson趋势滤波。两个F检验和Kruskal-Wallis检验结果表明,在0.1%和1%显著性水平下,食品价格指数中不仅存在稳定的季节性,还存在移动的季节性,即食品价格指数不仅随月波动,还随年波动。1%显著性水平下接受了原假设,说明经过调整后的序列已经分离出了所有的季节性。

表5 食品价格指数残差季节性检验
3.3 季节调整结果分析
季节调整的主要目标在于通过剔除季节成分,更加直观地分析所选变量的内在规律和趋势。模型通过检验之后,得到季节调整后的序列。图3表示季节调整序列和原始序列的趋势。从图3可以看出原序列具有明显的季节性,经过季节调整后序列总体上变得平滑。由季节调整序列可以看出,我国的食品价格指数大致可以分为两个阶段,第一阶段:从2001年到2003年下半年,这一时期食品价格指数变化不大,说明期间的食品价格稳定,没有大幅变化。第二阶段:从2003年下半年到2015年,这几年的食品价格指数呈现长期增长趋势,其中2008年到2009年之间有短暂下滑,下滑原因则与全球金融危机有关。2008年的世界金融危机抑制了我国经济增长,使得食品价格指数出现下降的趋势。
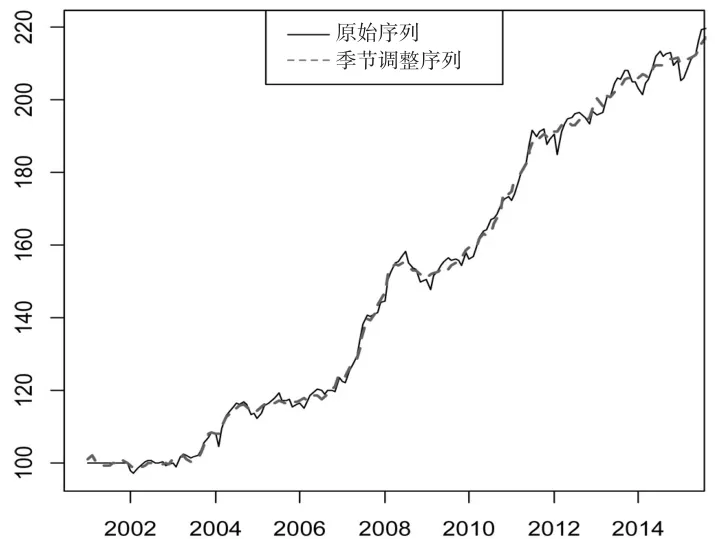
图3 食品价格指数及其季节调整序列时序图
图4为食品价格指数的季节因子和春节效应趋势图,容易看出分解出的季节因子的影响显著不同于春节效应,季节性成分波动明显,并且不同年份季节性强弱不同,季节性成分在2001年对食品价格指数影响较小,之后影响慢慢增强,2008年达到高峰,之后有所下降,此后几年,季节性成分保持在一个比较稳定的程度,表明季节性成分对食品价格指数的影响比较稳定。就单个年份来看,在每年1月份左右,食品价格指数会呈现出一个高峰期。之后,人们对食品商品的需求会随着节日气氛的消退有所下降,进入全年的低谷期。接下来食品价格指数会在每年的7月份左右又呈现第二个高峰期,随后又会下降。春节效应主要是春节节日消费因素的影响,春节效应会使食品需求量增加,带动价格上涨,从而导致食品价格指数上升。春节的影响基本集中在1、2、3月份,对其他月份没有影响。
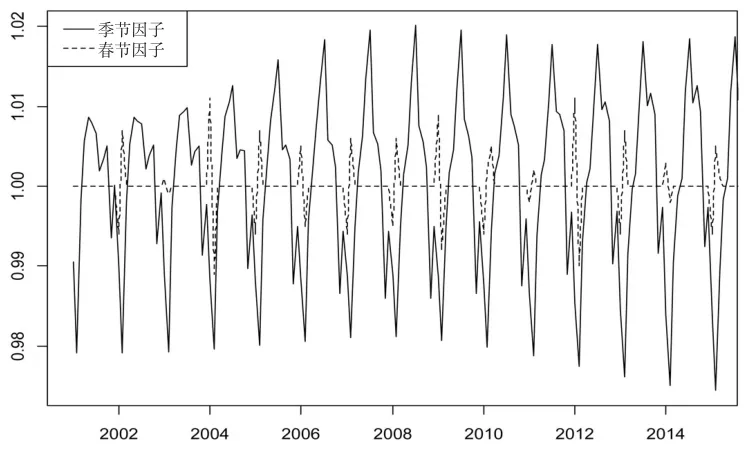
图4 食品价格指数的季节因子和春节因子
4 模型预测
对食品价格指数的同比数据进行处理后,得到定基比数据,然后运用本文中考虑春节效应的X13-A-S方法进行季节性调整,最后得到的调整效果是令人满意的,运用该方法对我国2015年10月至2016年9月的食品价格指数进行预测,得到的结果如表6所示,并把实际数据与预测结果进行对比,得出相对误差。
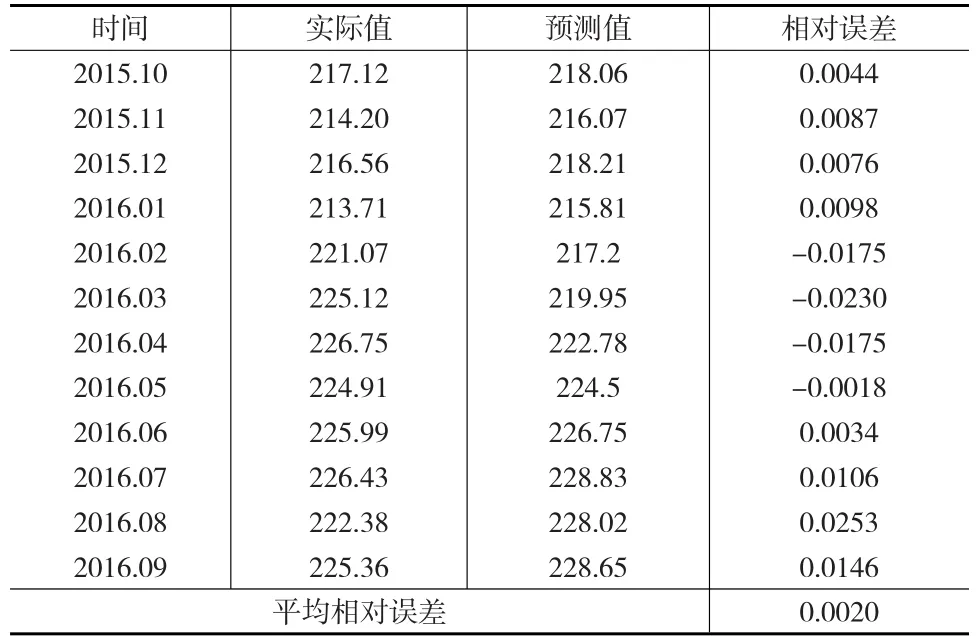
表6 食品价格指数预测值与实际值对比表
从表6可以看出,运用X13-A-S对我国食品价格指数月度数据的预测结果与真实值相差很小,模型的相对误差非常小,进一步说明季节调整的效果令人满意。
5 结论
本文根据2001年1月至2016年9月、以2001年为基期的食品价格指数数据,使用最新的X13-A-S方法对其进行季节调整,考虑了我国特有的移动假日春节,模型显示春节的节前和节后效应都很显著,而且对食品价格指数有正向作用;检测的异常值只有1个,为2008年2月;确立模型为(0,1,1)(0,1,1)季节调整模型,通过季节性检验和残差季节性检验,其不仅存在稳定的季节性,还存在移动的季节性;M1~M11、Q统计量都小于1,构建的模型较合理。最后使用本文的模型对2015年10月至2016年9月的食品价格指数进行预测,预测值与实际值非常接近,能够很好地预测我国食品价格指数的走向。
参考文献:
[1]Bell W R,Hillmer S C.Issues Involved With the Seasonal Adjustment of Economic Time Series[J].Journal of Business and Economic Statistics,1984,(92).
[2]Findley D F,Monsell B C,Bell W R,et al.New Capabilities and Methods of the X-12-ARIMA Seasonal Adjustment Program[J].Journal of Business and Economic Statistics,1998,(2).
[3]陈雄强等.货币供应量的实时监测——基于季节调整方法[J].上海经济研究,2011,(7).
[4]李静等.我国食品价格变动的属性特征——基于1996—2010年季度数据的实证分析[J].政府经济管理,2011,(9).

