基于预测区间理论的工程造价信息数据统计测算模型

李泽阳，刘 玲，胡奕仁

（1.武汉科技大学 管理学院，武汉430081；2.中国地质大学（武汉）工程学院，武汉 430074）

0 引言

“大数据”具有“5V”特征，即数据类别多（Variety）、数据体量巨大（Volume）、处理速度快（Velocity）、数据真实性（Veracity）、价值密度低、商业价值高（Value）[1]。工程造价信息包含政策法规、招投标信息、计价依据、价格信息、指数信息、指标信息、社会平均成本、社会平均利润以及典型工程案例分析等，其具有大数据的特征，属于大数据的范畴[2]。随着对招标的建设工程实行“五价”备案制度，由建设项目的投资估算、设计概算、招标控制价、合同价、竣工结算等文件的书面及电子数据资料形成工程造价信息大数据[3-5]。

建安造价是工程造价构成中最基本、最重要的部分。可通过及时、真实地统计测算工程造价信息数据以快速、精准地计算新建工程的建安造价[6]。由于建安造价统计测算的影响因素多，变动幅度大[7]，所以目前工程造价主管部门发布的单位造价指标仅是对其均值的测算，未能对同地区、同类工程的单位造价取值区间及其概率做出精确的统计和测算[8]。本文运用统计学方法测算工程造价共享指标，及时、真实地随机抽样并处理工程造价信息数据，以贝叶斯学派思想为指导，并运用正态模型参数估计、卡方拟合检验、预测区间估计等方法[9-11]，测算出同地区、同类工程的单位造价区间及其概率，为测算新建工程的建安造价及建设投资提供指标和参数，为工程造价信息大数据的挖掘及应用提供一种科学、合理的统计测算方法[12-14]。

本文旨在运用统计学方法解决单位造价测算中存在的离散性、随机性、不精确性等问题。首先，对原始数据进行预处理，降低时效性、区域性、工程类别等因素对测算结果的影响；然后，结合贝叶斯思想和相关经典统计学理论[9-11]，构建工程造价信息数据统计测算模型；最后，测算出单位造价的预测区间及其概率，以快速、精准地测算新建工程的建安造价及投资估算。

1 研究方法

点估计和区间估计为未知参数提供了很好的信息[10]。有时，相对于总体均值，人们对预测未来观测值更感兴趣。例如，在对工程造价信息数据统计测算研究中，需要利用观测数据来预测一个新的观测结果，即投资者对预测新建项目的工程造价更感兴趣。估计工程造价的均值和置信区间，只能为新建项目工程造价测算提供一个大致的定位。投资者需要一个关于单个观测的不确定性说明，而预测区间的建立可以满足快速、精准地测算新建工程造价的要求。

假设随机样本是从未知均值、已知方差的正态总体里得到的[11]。新观测结果的点估计值为,点估计值的方差为。在新观测中随机误差的方差是σ2。由于新观测值x0与样本均值是独立的，且预测方差是单一观测随机误差的方差和估计均值的方差之和，所以可构造统计量如式（1）所示：

z服从n(z;0,1)。如果利用Z统计量的概率式（2），且将x0置于概率语句的中心，则式（3）成立。

2 工程造价信息数据统计测算模型构建

2.1 原始数据的处理

对同地区、同类工程的单位造价进行随机抽样。首先，取同地区、同类工程的单位造价的样本数据，依据资金时间价值已知现值求终值的等值换算公式（5）[2]，将随机抽样的单位造价原始数据换算到同一时点。

处理后的单位造价记为x1,x2,…,xn；由于模型是通过样本来研究总体，而总体可能出现任何情况，因此可以采用连续性修正，记频率分布直方图横坐标的覆盖区间为R；其次，对单位造价按大小排序并确定适当的组距，统计落在每个区间的样本频数fi，计算得出频率；最后，以组距为横坐标、以频率为纵坐标绘制样本分布频率直方图，观测样本数据近似来自于某种分布总体。

2.2 极大似然估计

随机抽样收集单位造价样本观察值，由于单位造价可看作类似于样本均值的统计量，因此根据中心极限定理，绘制的样本分布频率直方图最有可能类似正态分布。模型假设随机样本来自参数为μ，σ的正态总体，即同类工程的单位造价总体服从正态分布，记分布函数为F（x;μ，σ)。根据极大似然估计原理，X的概率密度函数为式（6），似然函数为式（7）[11]：

对其求偏导得式（9）：

式（10）即为同类工程的单位造价总体期望和方差的估计值。

2.3 卡方拟合检验

总体所属分布类型的假设是依据观测随机样本频率分布图得出，需要进一步检验，以上文计算得出的估计值作为参数值对分布类型进行拟合检验，检验其是否服从正态分布。设x服从正态分布，分布函数记作F(x;μ,σ)，将x取值的全体Ω划分为k个互不相交的子集A1,A2,A3,…,An,将样本观察值x1,x2,x3,…,xn出现在Ai的个数记作2，3...k)，则事件＝Ai{x值在Ai内}的频率为。计算事件的概率，得pi＝P(Ai)，i=1,2,3…,k。通常频率与概率存在差异，当试验次数足够多时，这种差异将减少并可以忽略不计，即不应该太大，采用形如式（11）的统计量度量样本与假设分布的拟合程度，其中Ci（在每一项前乘以适当的Ci，是为了使得统计量(11)有一个理想的极限分布）为常数。根据皮尔逊定理[10]，取，采用式（12）作为检验统计量。

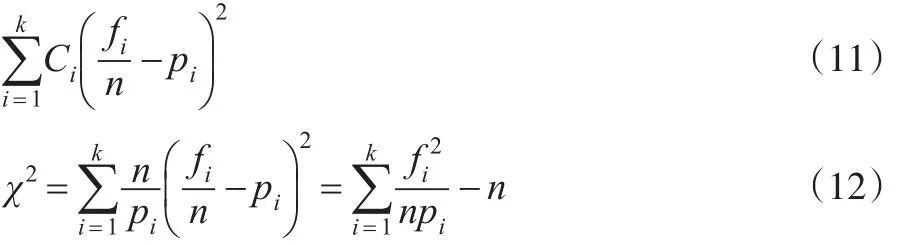
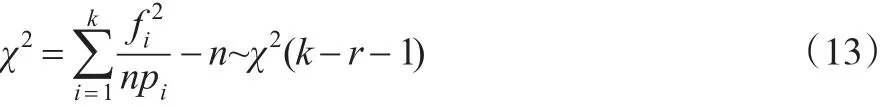
当X服从正态分布时，则式（13）成立。

此时χ2不应该太大，拒绝域为χ2≥G=χ2(k-r-1)。最后检验式（14）是否成立。

α为显著性水平。不等式成立时拒绝原分布服从正态分布，否则就“不拒绝”原分布服从正态分布，即随机样本来自正态总体。

2.4 预测区间估计

检验随机样本正态性则可进行预测区间估计。在实际应用中，单位造价的总体期望和方差是未知的，总体期望和方差的估计值均为统计量，不是定值，若将估计值作为参数值直接导入统计量中进行预测区间估计则势必会影响计算结果的精确度，造成系统误差。当n较大时student分布与正态分布相似，统计测算模型用student分布取代正态分布，用s代替σ进行运算，根据预测区间估计理论构造新的统计量，如式（15）：

t服从自由度为n-1的student分布，运用T统计量的概率，见式（16）：

将x0置于概率语句的中心，式（17）所描述的事件发生的概率是1-α。

未来观测x0的100（1-α）%的预测区间为式（18）：

3 实证

随机抽样收集某地区2013—2015年多层商品房住宅楼竣工结算的单位建安造价。如表1所示。

年折现率i取2012年末央行发布的贷款利率，即i=6.15%，将表1中2013年和2014年的单位造价，根据资金时间价值的等值换算方法，如公式（5），换算成同一时点的单位造价，整理数据如表2所示。

对数据进行统计与分析，多层商品房住宅楼单位建安造价在（0,1500）区间的频率为2%，单位建安造价在（1500,1550）区间的频率为7%，单位建安造价在（1550,1600）区间的频率为16%，在（1600，1650）区间的频率为47%，在（1650,1700）区间的频率为21%，在（1700,1750）区间的频率为5%，(1750,+∞)区间的频率为2%，单位造价区间及频率分布直方图，如图1所示。

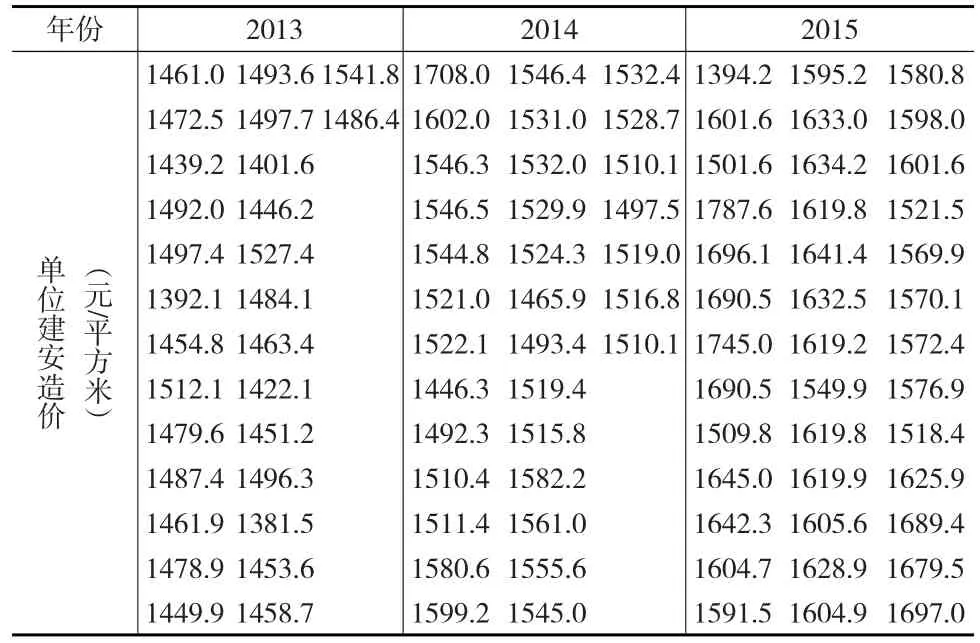
表1 某地区多层商品房住宅楼单位建安造价

表2 单位建安造价区间及频率

图1 某地区多层商品房住宅单位建安造价频率分布图

假设某地区单位造价符合参数为μ，σ的正态分布，记为X～N（μ,σ2）。设μ，σ为未知参数，x1,x2,… ,x100是来自X的样本值，样本均值为1626.3，样本方差S2为3893.76，n为100，运用极大似然法估计法求得μ=1626.3，计算得出σ=62。以估计值作为参数值，计算时间Ai的概率，得pi=P(Ai)，pi与fi的计算结果，如表3所示。

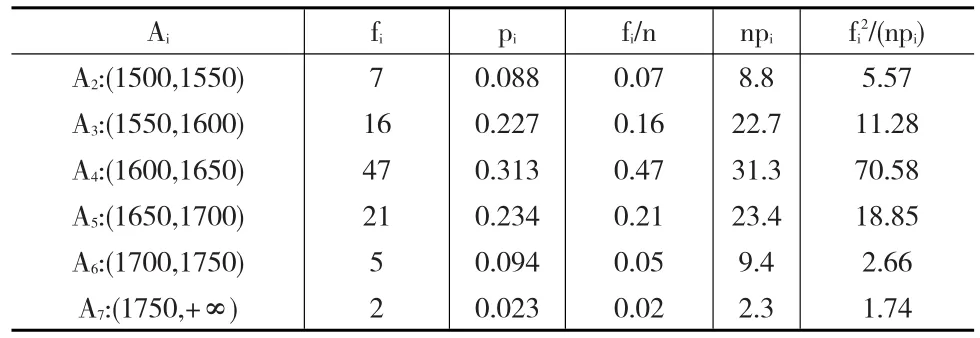
表3 卡方拟合检验的结果

由表3得x2＝112.58-100=12.58，依据卡方分布临界值表可知：故在显著性水平0.05下，可认为该组随机样本数据来自正态分布总体[15]。

根据所构建的预测区间估计模型，取显著性水平α为0.05，统计测算单位造价区间为（1501.5，1751.0），随机观测结果在预测区间的概率为0.95，区间幅度为16.6%，单位造价在此区间内任意点均满足建安造价测算的误差要求。取显著性水平为0.1时，预测区间为（1522.1，1730.5），随机观测结果在此预测区间的概率为0.90。同理，模型也可测算出不同显著性水平下的单位造价预测区间。

一次随机试验发生的概率小于0.05即为小概率事件，通常认为小概率事件是不会发生的，即新建工程的单位建安造价一定在显著性水平为0.05的预测区间范围内。不同显著性水平的单位造价预测区间可满足不同建设工程对预测区间精准度的需求，为快速、准确地测算新建项目的工程造价和科学地投资决策提供模型方法和参数支持。

4 结论与讨论

（1）本文构建了基于预测区间理论的工程造价信息数据统计测算模型，并通过实证研究测算出同类工程的单位造价预测区间及其概率，为测算新建同类工程的建安造价和投资估算提供指标和参数，也为全寿命周期工程造价主动管理提供模型和方法。

（2）模型对工程造价信息原始数据进行预处理，减少时效性、区域性、工程类别等因素对测算单位造价的影响，降低了随机误差。以贝叶斯学派思想为指导，将μ，σ等参数作为统计量，不直接使用其估计值，用样本均值和样本方差导入模型中运算，避免了系统误差，提高了测算结果的精确度和可靠性。

（3）模型适用于工程造价信息数据的统计与测算，针对工程造价信息数据区域性和时效性的影响，采用指数调整或进行等值换算，将数据导入统计测算模型即可得测算结果。模型方法运算简便，科学合理，精确度高，易于计算机编程，模型方法可广泛应用于各种信息数据的统计、分析和测算。若后续研究抽取的样本数量足够大，并对处理原始数据的方法加以改进与完善，则模型测算结果会更精准，应用范围也会更加广泛。

参考文献：

[1]陶雪娇,胡晓峰,刘洋.大数据研究综述[J].系统仿真学报,2013,(8).

[2]俞立平.大数据与大数据经济学[J].中国软科学,2013,（7）.

[3]沈祥华,姚甫昌,王红兵.建筑工程概预算[M].武汉：武汉工业大学出版社,2008.

[4]冯斌,张建中.工程造价资料积累技术经济分析指标体系设计及在Excel软件环境下的应用[J].内蒙古工业大学学报,2005,(11).

[5]彭大敏,王罕.大数据环境下工程造价管理对策分析[J].建筑经济,2014,(11).

[6]陈小龙,王立光.基于建筑设计参数分析模型的工程造价估算[J].同济大学学报,2009,37(8).

[7]林琴.编制建设工程造价指标的探讨[J].建筑经济,2005,(2).

[8]吴学伟.住宅工程造价指标及指数研究[D].重庆：重庆大学硕士论文,2009.

[9]陈家鼎，郑忠国.概率与统计[M].北京：北京大学出版社,2004.

[10]Navidi W.Statistics for Engineers and Scientists[M].China：Tsinghua University Press,2012.

[11]Ronald E.Walpole R H，Myers Sharon L.Probability and Statistics for Engineers and Scientists(Eighth Edition)[M].China：China Machine Pres,2010.

[12]Dong J,Wei FJ.A Study on Life Cycle-Oriented Analysis Method of Project Cost[J].The 1st International Conference on Information Science and Engineering，2009.

[13]董士波,郑立新.全生命周期工程造价成本分析模型研究[J].9th Pacific Association of Quantity Surveyors Congress,2005.

[14]Dietterich T G,Michalski R S.Learning to Predict Seguences,Machine Learning[M].An Artificial Intelligence Ap-proach,1986.

[15]余建英，何旭宏.数据统计分析与SPSS应用[M].北京：人民邮电出版社,2003.