基于Logistic回归法的企业财务风险预警模型构建
李长山
(吉林工商学院 会计学院,长春 130507)
0 引言
财务风险预警系统有三种重要的功能,分别是:(1)提前预知风险。在企业的财务情况出现危机之前必须要收集企业的经营情况和经营报告,对两者进行比较得出最好的方法,才能在财务出现预警之前减轻或者避免风险对财务带来的损失。(2)提前控制风险。当财务出现危机的时候也不用担心,及时分析财务的资料,要找到根源才能阻止财务风险进一步扩大,才能找到合适的方法进行预防,从而避免发生严重的财务风险。(3)提前防范风险。财务风险发生的原因、解决财务风险的措施以及处理财务风险的结果是通过定量和定性分析得出的,企业财务管理和经营中的不足可以通过制定新的财务活动来改善,从而消除隐患。
国外的学者对企业财务风险预警的研究比较深入。如等Altman等(2016)[1]早前就对美国的企业破产进行了预测,不过只能通过多元判别分析的方法进行预测。Ohlson等(2015)[2]学者采用Logistic回归法对企业的财务风险构建了预警模型,并对样本公司的破产概率进行了分析。Logistic回归模型并没有对变量分布提出具体的要求,而且在回归时预测了概率值,实用性较好。Aguilera等(2016)[3]研究了Logistic回归和主成分的分析。不过因为主成分的分析比较难解释,所以模型的建立才会涉及技术学习。Hernandez等(2009)[4]提出了能够保留最优子集优点的方法,那就是LASSO方法,使用这种方法可以同时运行变量选择和参数估计。
而在国内,相关的研究也很多。如赵健梅等(2014)[5]就对公司的财务风险预警进行了实证研究。鲜文铎等(2015)[6]通过Logistic模型对上市的公司进行了预测。邓晶等(2015)[7]则对上市公司的信用风险进行了预测,通过因子的分析和Logistic模型的结合得出结果。王小燕等(2015)[8]对信用评分模型进行了研究实证。
财务指标以及样本选取都会对财务风险预警模型产生限制作用。财务指标的选择会因模型的不同而有所侧重,从而忽略财务指标受其他方面的影响,另外,财务风险预警模型的适用性也受不同行业的影响。因此,本文选取的财务指标主要来源于“中国上市公司财务指标分析数据库”,采用Logistic回归法构建企业财务预警模型具有较强的指导作用。
1 Logistic回归法的逻辑回归与指标选择
1.1 Logistic回归法
本文中的模型是通过概率高的逻辑回归进行创建的。因变量是线性回归中的基本设立,所以该模型中包含了定性变量。假设Y值有两个可能性,分别是0和1,其中0代表的是企业的财务风险,1代表的是企业的财务状况。线性模型Yi=β0+β1X1在这种情况下是不符合其假设的,不过Yi是0和1的分布,所以其均值在模型中具有特殊的含义,比如:

由此可以得出Y值:
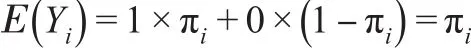
上式中的πi值代表概率值,符合基本设立的线性回归,所以这里可以用线性模型进行拟合,不过最好使用多维逻辑回归模型,如果使用线性模型会产生一系列的影响因素。根据原理得出以下公式:
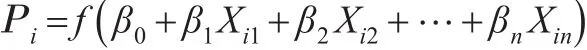
可以将Yi用另一种方式来表达:

对似然函数选用最大似函数法得出的对数有:

代入上式,得出下列方程式:

在此方程式中要想使其导数为0,就要运用最大似然估计值求回归系数中的变量,若其导数不是0,似然数就取最大数值。
1.2 指标选择
企业的财务风险危机通常是长期形成的,因而在选取采取预警指标时应当选取2015—2016年近两年的指标,这样能更明确地分析财务风险产生的原因。本文的样本数据来源于“中国上市公司财务指标分析数据库”,本主要为23家2016年制造业上市企业的数据指标,与之对应地抽取了30家2016年非上市公司的年报指标、分组检验指标,并对相关指标进行筛选。
初步筛选上市公司的数据指标发现,可持续增长率这一指标在不同上市公司中并不存在。本文经过检验相关财务指标发现,资产净利率、销售费用率、净资产收益率和财务费用率反映盈利的能力;流动和速动比率反映短期偿债的能力;股东权益相对年初增长率、营业收入增长率反映其成长性;应收账款周转率、存货周转率反映营运的能力;流动负债比重与流动负债占总资产的比重反映长期偿债的能力,考虑到其常见性和实用性,不能将其加入到模型的构建中。可以将有财务风险的公司和没有财务风险的公司分为两组进行检验,看其均值是否相同,如果Sig比较小则该指标可以保留下来。
在检验中如何判定其方差是否一样,如果第一列的Sig值比0.15大就说明方差是一样的,相反就说明不一样。因此先对第一列中的Sig值进行判断,而判断其差异是否明显则是判断第二列中的Sig值,如Sig值比较小且变量的系数不是0,那么差异就会很明显,所以要先对其进行多重共线性判断才能构建逻辑回归模型,方差扩大因子法和特征根条件数法是构建逻辑回归模型的主要方法。将Xj=1/(1-Rj)(1+Rj)定义为方差扩大因子,用Rj和Xj分别代表自变量和自变量的决定系数。矩阵之间的各个特征根之积就等于矩阵的行列式,而特征根条件数法就是来自于矩阵。特征根是根据行列式的变化而变化的,只要有一个特征根等于0,必定会存在多重共线性。将定义为条件数,其中用λm代表特征根的最大值,用Ki代表特征根,用λi代表条件数。判断矩阵的特征根消散程度和多重共线性可以用条件数来判断。通常情况下,K值在[0,10]范围内时,矩阵不存在共线性;当K值在(10,100]范围时,矩阵的共线性较强;若K值大于100时,矩阵的共线性则比较严重。
1.3 逻辑回归
通过相关软件对三变量进行逻辑回归,得出结果如表1所示。

表1 变量的逻辑回归结果
从表1中可以看,出sig值比wald统计量检验更加明显,因为不能使用假设,故取Sig值最小化。在Sig值下的股东权益增长率很明显但是变量不明显,因此可以将其删除。对删除后剩下的变量再进行逻辑回归如表2所示。

表2 变量第二次逻辑回归结果
从表2中,可以得出方程式p=exp(-2.753-0.494X1+0.061X2)/1+exp(-2.753-0.494X1+0.061X2),净资产收益率(平均)用方程式中的X1代表,流动负债比率用X2代表。将0.5作为财务风险临界值,若该值大于0.5则说明具有财务风险。以此数值对比几家正常经营的企业发现正确率为100%,但该模型仍存在许多不足。若以0.5作为比较值,两家企业的p值分别为0.52、0.48,此情况下并不能对企业的财务状况进行判断。例如,企业所在行业的地位和公司发展的产业中的变量并未涉及到构建的模型,就不能说明企业的财务情况和发展情况,因为数据不全面。
2 实证分析
2.1 Wilcoxon秩检验
本文选取了23家上市企业以及30家非上市企业的财务数据为研究对象进行Wilcoxon秩检验,通过Wilcoxon秩检验可以得出Wilcoxon秩检验结果如下页表3所示。
2.2 因子分析
通过少数的潜在因子将预测的多个指标与潜在因子的线性结合起来被称为因子分析。将财务比率的指标进行因子提取主要是为了克服变量之间的共线性又要保留财务比率变量的信息。先对KMO进行检验,检验的结果得出文中所选取的财务比率变量是适合做因子分析的,通过下页表4可以知道6个主因子的方差贡献率等于82.278%。
通过对因子相关矩阵的总结和归纳得出下列主因子分析法,如表5所示。

表3 Wilcoxon秩检验结果

表4 主因子的特征值和方差贡献率

表5 主因子分析法
从表5中可以看出,因子F1与以下12个不同指标之间有关联,分别是 X1、X2、X3、X4、X5、X6、X7、X8、X9、X35、X40、X41,以此可以将他们归为一类。从其意义上看,公司的债务情况可以用F1来表示;企业的获利情况可以用F2来表示,企业的权益增值能力可以用F3来表示;企业的资金周转能力可以用F4来表示;企业的股东获益能力可以用F5来表示;企业的资产增值能力可以用F6来表示。
2.3 回归模型预测检验与结果
2.3.1 模型回归
本文选取的财务困境企业和非财务困境企业用数据0和1来表示,通过因子分析中得出的几个主因子和Logistic回归模型可以得到以下的模型拟合优度检验结果。其中Loglikeihood的似然值为7.612,Cox&Snell的统计量为0.548,Nagelkerke的统计量为0.917,这说明该模型的效果非常好。
因为本文模型中的因子F4、F5、F6表现不明显,所以只选取了F1、F2、F3三个因子对其做出了估计系数以及统计量(见表6)。当主因子变量的系数在企业财务困境预警系统中为正数时,说明主因子的P值增大其F值就会增大,而F值代表的财务情况也会增大;当主因子变量的系数中哪个系数最大,说明那个系数代表的企业获利状况是最好的,那么该企业的财务状况也就越好。所以只有增加企业的获利能力才能让企业摆脱财务危机。
举例进一步分析企业的财务比率和困境之间的关系,用F1代表债务状况的主因子,其是受现金流量比率、权益负债比率、流动比率和债务保障率的影响而变化的,说明这些比率提高F1就会增加,同时P值就会跟着增大,那么企业的财务陷入困境的几率就会越少。相反,其也受财务费用率和资产负债率的影响而变化,说明F1是随着这两个比率的减少而增加的,其增加了P值才会增大。

表6 最终模型的估计系数及其统计量
从而得出了以下的回归模型:

其中,Yi=6.924+1.148F1+11.598F2+1.162F3。

此回归模型中主要有三个因子,依次是F1、F2、F3,而这三个因子分别代表了不同的情况:F1表示的是企业中的债务情况;F2代表的是企业的获利情况;F3代表的是企业的权益增长能力。
2.3.2 最终模型的预测结果
通过上面Logistic回归模型得出的结果,对不同企业进行判定,用0.5作为临界值,如果0.5比P值小,就判定为正常的企业,反之就判定为财务困境企业。该模型的预测效果如下页表7所示。

表7 预测效果判定
从表7可知,其总体预测的准确率在98.6%,说明预测的结果与本文所选取的企业债务状况、权益增值能力以及获利状况是有关的。
3 结论
本文通过明显的指标体系对财务风险进行主成分分析,并且搜集了正常企业和非正常企业的财务数据创建了Logistic回归法财务预警模型,该模型能使企业拥有者第一时间意识到财务的风险和危机。
本文通过Wilcoxon秩检验对不同企业的财务进行了比较,选出了几个财务状况比较好的企业进行分析,建立了Logistic回归模型,从而获取了准确性比较高的企业财务困境预警系统。主要有以下几个结论:
(1)主因子变量的系数中哪个系数最大,说明那个系数代表的企业获利状况是最好的,那么该企业的财务状况也就越好。所以只有增加企业的获利能力才能让企业摆脱财务危机。
(2)用X1代表流动比率,X2代表速动比率,X3代表现金流量比率,X7代表权益负债比率,将这些系数作比较可以发现其对F1的影响是非常大的,所以要对判定财务的指标特别重视。
(3)通过上面的统计分析得出的主因子和财务指标以及Logistic回归模型,创建了企业财务预警系统,该系统的准确率非常高。由此可知,可以通过财务困境预警系统知道该企业是否会陷入财务困境,从而解决问题。
参考文献:
[1]Mousavi Shiri S M,Tabarestani M R.The Ability of a Model Based on Logistic Regression in Prediction of Financial Distress and Effectiveness of Efficiency Score in Improving the Model[J].Circulation,2016,122(14).
[2]Li H,Wang Y,Zhao P,et al.Cutting Tool Operational Reliability Prediction Based on Acoustic Emission and Logistic Regression Model[J].Journal of Intelligent Manufacturing,2015,26(5).
[3]Balasch S,Romero R,Ferrer A.A Logistic Regression Model Applied to Evaluate the Influence of Operating Time of AgI Ground Acetonic Generators on the Size and Hardness of Hail[J].Natural Hazards,2016,32(3).
[4]Hernandez D J,Han M,Humphreys E B,et al.Predicting the Outcome of Prostate Biopsy:Comparison of a Novel Logistic Regression-based Model,the Prostate Cancer Risk Calculator,and Prostate-specific Antigen Level Alone[J].Bju International,2009,103(5).
[5]赵健梅,徐晶,张国平,张芳华等.基于Logistic回归的区域地质灾害综合气象预警模型[J].气象,2014,33(12).
[6]鲜文铎,杨蓬勃,张成虎,张湘.基于Logistic回归分析的上市公司信贷违约概率预测模型研究[J].经济经纬,2015,(2).
[7]邓晶,刘先伟,陶萍.基于Logistic回归模型的建材业上市公司财务预警研究[J].工程管理学报,2015,25(4).
[8]王小燕,张立军,刘菊红,刘丹.上市公司财务危机预警的Logistic回归分析[J].南昌大学学报:理科版,2015,31(3).

