用于气固两相流测量的方形静电传感器阵列建模及实验验证
张帅,闫勇, 2,钱相臣,胡永辉
用于气固两相流测量的方形静电传感器阵列建模及实验验证
张帅1,闫勇1, 2,钱相臣1,胡永辉1
(1. 华北电力大学 控制与计算机工程学院,北京,102206; 2. 肯特大学 工程与数字艺术学院,英国 肯特,CT2 7NT)
为研究由分布式条形电极组成的方形静电传感器阵列检测机理,基于静电学基本理论及镜像电荷法建立方形静电传感器阵列的解析式感应机理数学模型;基于该模型,采用点电荷模拟带电颗粒,研究在管道内不同区域处的移动带电颗粒激励下,静电传感器阵列中不同电极的感应电荷及感应电流输出特性。为验证数学模型,设计并搭建方形管道重力输送颗粒实验装置。方形静电传感器阵列包含2层分布式条形电极组,每层条形电极组中12个(3×4)条形电极均匀分布在方形管段截面的四面管壁上。控制颗粒在管道横截面不同位置下落,研究静电传感器阵列输出特性。研究结果表明:方形静电传感器阵列各电极的感应输出结果与仿真结果趋势一致,证明了数学模型的有效性。
气固两相流;方形管道;静电传感器;数学建模;镜像电荷法
利用一定压强和速度的气流通过封闭管网来输送物料,是食品加工、冶金、火力发电等现代工业中普遍采用的粉状物料输送方式[1]。气力输送管网多采用圆形截面管道,但方形截面管道由于制造工艺简单、安装方便,在烟气排放管道、循环流化床及部分火力发电厂中也得到了广泛应用[2]。管道内气流带动粉体流动,属于典型的气固两相流,其流动状态的在线检测一直是学术界和工业界的热点和难点。以火力发电厂为例,电厂利用热风将粉体燃料通过气力输送管网送至锅炉燃烧,粉体燃料流速、流量、流型等流动状态的有效监测,有助于电厂锅炉的安全、高效运行以及节能减排。但由于在输送过程中,管道内粉体颗粒与输送气流之间(气固两相)的相间力非常复杂且时刻变化,粉体流动状态监测非常困难。粉体颗粒在管道内输送过程中,颗粒与管壁、输送气流及其他颗粒碰撞摩擦,表面会携带静电电荷。静电传感器利用粉体颗粒在输送过程中产生静电这一现象,基于静电感应原理测量粉体的流动状态[3−8],具有结构简单、鲁棒性强、适用于恶劣工业环境等特点,在工业现场应用中具有显著优势。静电传感器按照传感器电极形状及安装位置的不同,分为非侵入式静电传感器、侵入式静电传感器或者两者的混合[9]。常见的非侵入式静电传感器电极有环形电极、弧形电极,侵入式静电传感器电极有棒状电极、星形电极、网状电极等,它们的工作特性也不尽相同。为更好地研究静电传感器检测机理、优化传感器设计,有必要建立静电传感器的感应机理模型。目前,已有研究者采用不同方法建立了不同形状电极的感应机理模型。针对环形电极,LAW[10]建立了基于点电荷的环形电极感应机理数学模型,得到环形电极感应电势和感应电荷与点电荷之间的对应关系。GAJEWSKI等[11]考虑电极本身电容对感应机理的影响,改进了感应机理模型,推导出环形电极感应电势与点电荷之间的解析关系。YAN等[12]进一步改进环形电极的感应机理模型,考虑了电极尺寸对感应电荷的影响,并分析了环形电极静电传感器的传感特性。针对静电传感器中其他形状的电极,XU等[13−14]采用有限元分析及计算机辅助设计方法分别建立了环形电极、弧形电极静电传感器感应机理的有限元仿真模型。KRABICKA等[15]基于有限元分析方法对比了棒状电极与环形电极的传感特性,优化了棒状电极的物理结构参数。上述各静电传感器均用在圆形管道上,方形管道由于管道横截面非圆心对称以及4个直角的存在,管道内粉体流动本身、静电场分布都比圆形管道内更加复杂[16],但针对方形管道的研究相对很少。MURNANE等[17]提出了方环形电极物理结构并建立了简化的感应机理模型。PENG等[18]进一步推导方环形电极静电传感器的点电荷感应模型,研究了方环形电极的感应特性。方环形电极静电传感器的特点在于可以测量方形气力输送管道内气固两相流在整个管道横截面上的平均流动参数,但不能获得管道内局部区域粉体的流动状态。由分布式条形电极组成的方形静电传感器阵列,将方环形电极分割成多个条形电极均布在方形管道四面管壁上,实现了方形管道横截面上局部区域粉体的流动状态检测[19]。为深入研究分布式条形电极组成的方形静电传感器阵列的感应机理和优化传感器设计,本文作者基于静电学基本理论及镜像电荷法建立方形静电传感器阵列的感应机理数学模型,研究传感器阵列的感应输出特性,设计并搭建方形管道重力输送颗粒实验装置,并通过实验验证了数学模型的有效性。
1 方形静电传感器阵列建模
1.1 传感器物理模型及检测区域划分
静电电极作为静电传感器的敏感元件,是获取气力输送颗粒流动参数及其变化信息的最基本部件,其电极结构及布置的设计直接影响测量系统的检测性能。由分布式条形电极组成的方形静电传感器阵列物理模型及传感器横截面检测区域划分如图1所示[19]。
静电传感器阵列由2层沿管道轴向相同布置的分布式条形电极组组成,单层条形电极组包含12个(3×4)条形电极,均匀分布在方形管段四面管壁上。同层的12个条形电极(依次标记为电极A至电极L),将传感器阵列横截面等分成9个测量区域,即:4个直角区域Ⅰ,Ⅲ,Ⅶ和Ⅸ,4个单面管壁区域Ⅱ,Ⅳ,Ⅵ和Ⅷ和1个管道中心区域Ⅴ。各电极与管壁之间通过绝缘层分隔,并与信号调理电路相连。
1.2 基于镜像电荷法的感应机理建模
粉体颗粒在管道内输送过程中,颗粒上携带的电荷、各电极上的感应电荷以及管壁之间相互作用,最终达到静电平衡状态下的三维静电场分布十分复杂。建立静电传感器感应机理模型是研究静电传感器感应特性、优化传感器设计的基础。本文作者基于静电学基本理论,采用镜像电荷法建立方形静电传感器阵列数学模型,模型坐标系在管道横截面上的投影如图2所示。
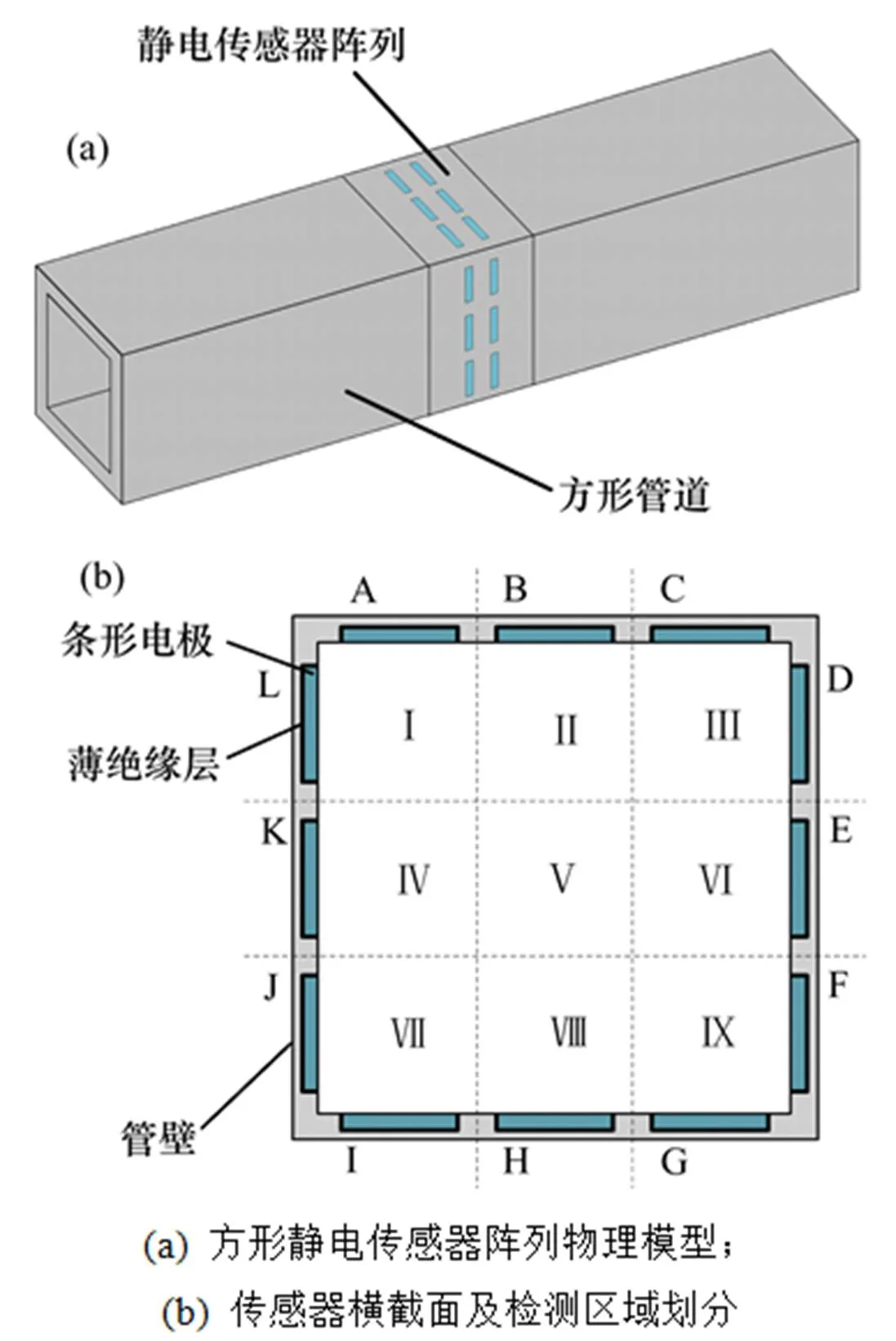
图1 方形静电传感器阵列物理模型及传感器横截面检测区域划分[19]

图2 方形静电传感器阵列数学模型坐标系
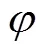

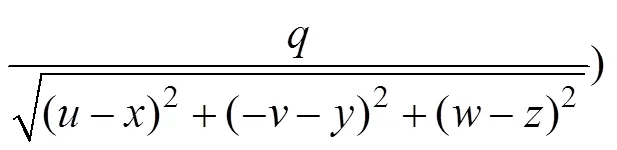
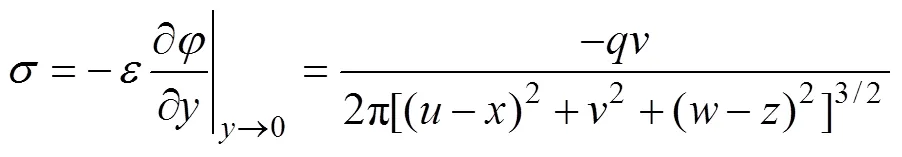


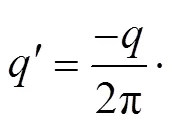
感应电流为感应电荷对时间的导数,即

2 传感器阵列感应输出
方形静电传感器阵列中条形电极的感应电荷与源电荷的电荷性质相反,感应电量与源电荷电量、源电荷位置以及电极长度、宽度和电极布局有关。为研究传感器阵列输出特性,假设电极长度和宽度固定,带有单位正电荷的点电荷分别在管道内3个有代表性的区域(中心区域Ⅴ、直角区域Ⅰ、单面管壁区域Ⅱ)内平行于管道轴线移动。基于上述感应机理模型,对相邻两面管壁上6个条形电极(电极A,B,C,J,K和L)的感应电荷及感应电流进行模拟,计算结果分别如图3~5所示。
从图3可以看出:当点电荷在区域Ⅴ内沿管道中心轴线移动时,由于电极B和K以及电极A和C,J和L分别与点电荷成对称分布,因此,对称分布的条形电极的感应电荷、感应电流输出曲线完全重合。另外,电极A,C,J和L与点电荷之间的距离较电极B和K与点电荷之间的距离远,因此,电极A,C,J和L的感应电荷及感应电流弱。为区分各电极的感应输出,避免电极与点电荷对称分布,点电荷移动轨迹平行但偏离相应区域的中心轴线,并将局部感应输出曲线放大显示(见图4~5)。从图4可以看出:当点电荷在直角区域Ⅰ内平行于区域Ⅰ中心轴线移动,且移动轨迹靠近面管壁侧时,电极A的感应输出明显强于电极L的感应输出,电极B的感应输出比电极K的输出略强,电极C和J由于与点电荷距离较远,输出弱,区分不明显。从图5可以看出:当点电荷在单面管壁区域Ⅱ内平行于区域Ⅱ中心轴线移动,且移动轨迹靠近面管壁侧时,电极B距离点电荷最近,感应电荷、感应电流最强,电极A,L,C,K和J与电荷距离依次递增,感应电荷、感应电流输出依次递减。由图3~5可知:传感器阵列对电荷的位置信息非常敏感,可以测量方形管道内气固两相流局部粉体的流动特征。同时,由于感应电荷极性与源电荷极性相反,通过传感器输出可以反推出粉体颗粒的带电信息。
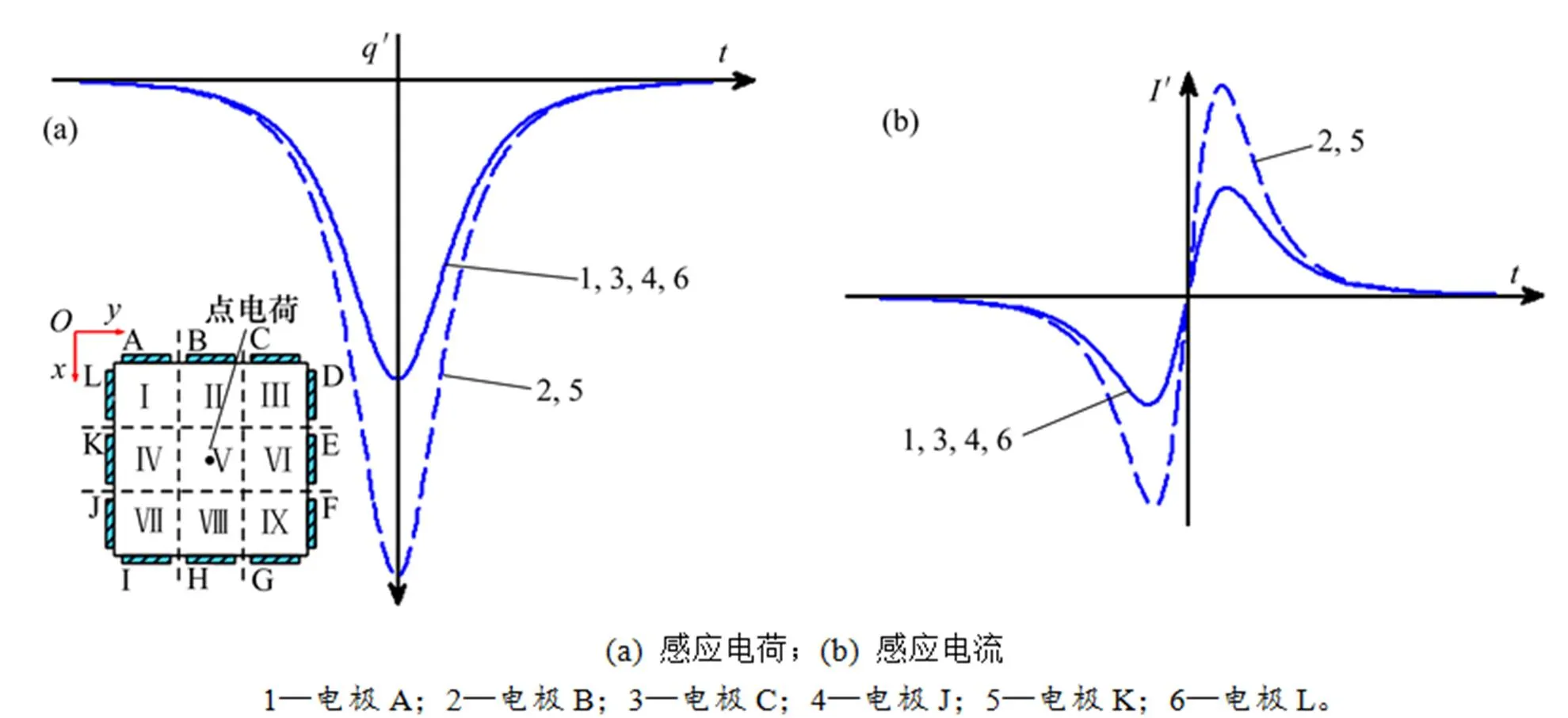
图3 点电荷沿区域Ⅴ中心轴线移动时电极上的感应电荷及感应电流
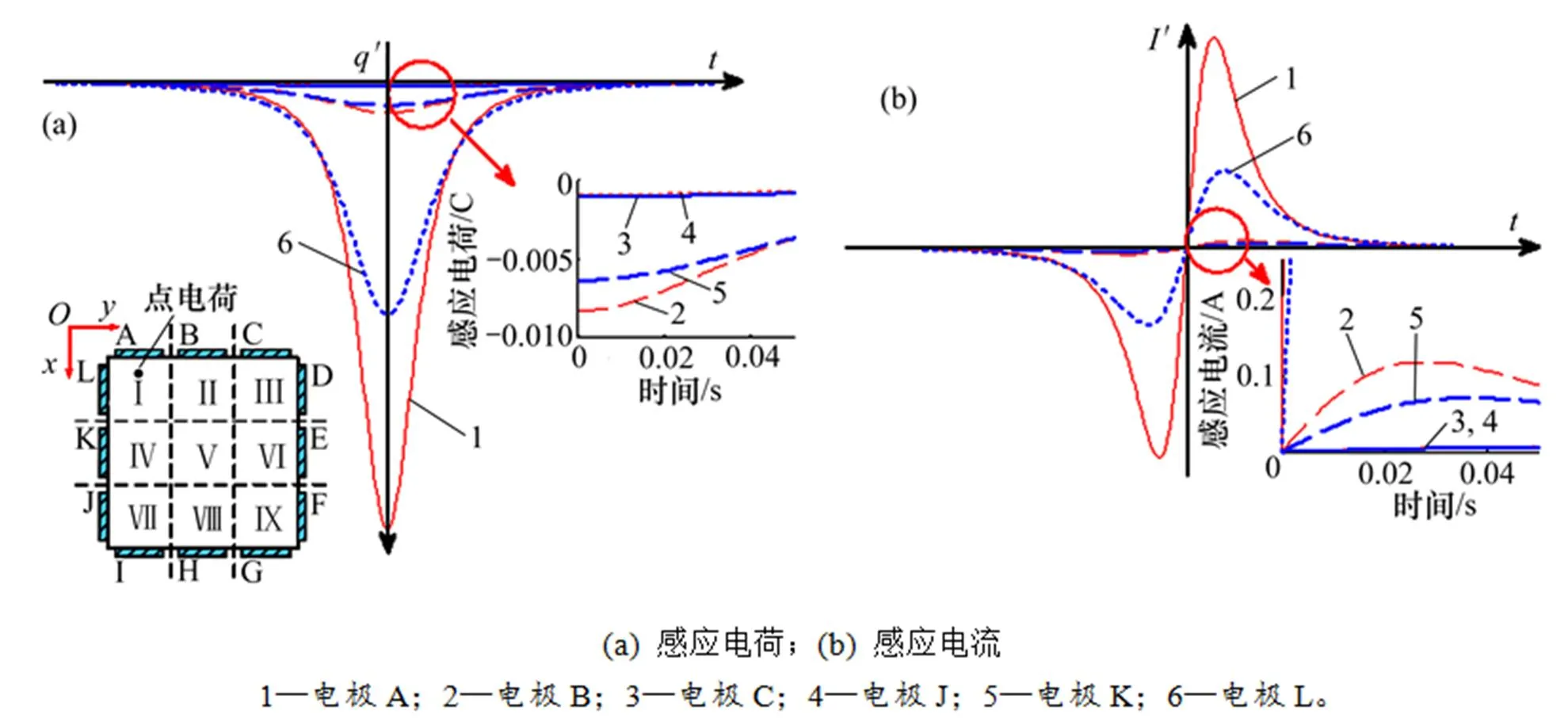
图4 点电荷在直角区域Ⅰ内平行管道轴线移动时电极上的感应电荷及感应电流

图5 点电荷在单面管壁区域Ⅱ内平行管道轴线移动时电极上的感应电荷及感应电流
3 实验研究及结果分析
为验证方形静电传感器阵列感应机理模型的有效性,搭建方形管道重力输送颗粒实验台,如图6所示。颗粒从漏斗进入导管顶端,通过自身重力在导管内垂直下落,穿出导管后流经方形静电传感器阵列。导管长为1.5 m,内径为10.0 mm,方形管段内壁边长为54.0 mm,通过调整导管与方形管段之间水平方向的相对位置,改变颗粒的运动轨迹。方形静电传感器阵列单面管壁的电极布置及尺寸如图7所示。6个条形电极分两层均匀分布在电路板上,每个条形电极长 15 mm,宽3 mm。为避免颗粒与电极直接接触产生电荷转移,造成传感器异常信号输出,电极表面覆有绝缘层。条形电极与信号调理电路相连,电极输出的感应电流信号经信号调理电路转换成电压信号,再经放大、滤波后,通过采集卡送至计算机输出显示。

图6 重力输送颗粒实验台

图7 单面管壁电极布置及尺寸(数据单位:mm)
在实验过程中,环境温度为24 ℃,空气相对湿度为51%,静电信号采样频率设为50 kHz。实验采用直径为4 mm的玻璃珠颗粒模拟点电荷。调整导管的水平位置,控制颗粒分别沿区域Ⅴ,Ⅰ和Ⅱ中心轴线穿过方形静电传感器阵列。传感器阵列两面相邻管壁上6个条形电极A,B,C,J,K和L的输出信号如图8所示。
由图8(a)可知:当颗粒经管道中心区域Ⅴ中心轴线流经传感器阵列时,各电极与颗粒距离均比较远,传感器整体输出较弱,其中电极B和K距离颗粒相对最近,输出最强,二者输出信号的峰峰值约0.23 V。由图8(b)可知:颗粒经管道直角区域Ⅰ中心轴线流经传感器阵列时,电极A和L距离颗粒最近,输出最强,其中电极L输出信号的峰峰值约3.2 V;其次为电极B和K,电极C和J因距离颗粒远,感应输出弱。由图8(c)可知:颗粒经单面管壁区域Ⅱ中心轴线流经传感器阵列时,电极B距离颗粒最近,输出最强,峰峰值约2.6 V;其次是电极A和C,电极L,K和J因距离颗粒较远,输出弱,但从局部放大图中依然可以看到,随着与颗粒的距离依次增加,电极L,K和J输出相应递减。由图8可知:传感器阵列敏感空间在管道轴向方向上的尺寸远大于条形电极的宽度,靠近颗粒处的电极输出强度大,传感器阵列可以区分颗粒的位置信息。
需要注意的是:在实验过程中,由于颗粒运动轨迹与区域中心轴线存在微小偏差,颗粒本身及颗粒表面的静电荷分布也并非绝对对称,导致与颗粒成对称分布的电极其实际输出曲线没有完全重合。另外,颗粒在下落过程中与空气之间不断产生摩擦起电以及电荷逸散[21],颗粒表面携带的电荷在时刻变化,并且颗粒受重力及摩擦力共同作用,颗粒处于非匀速运动状态,导致颗粒进、出电极敏感空间时,同一电极的感应电流输出不完全对称,如在图8(b)和8(c)中,颗粒向电极方向移动时,电极感应电流对应的负压信号幅值比颗粒远离电极时相应的正压信号幅值略强,而图8(a)中情况相反。图8中感应电流对应的电压都是先负后正,表明颗粒表面携带正极性电荷。
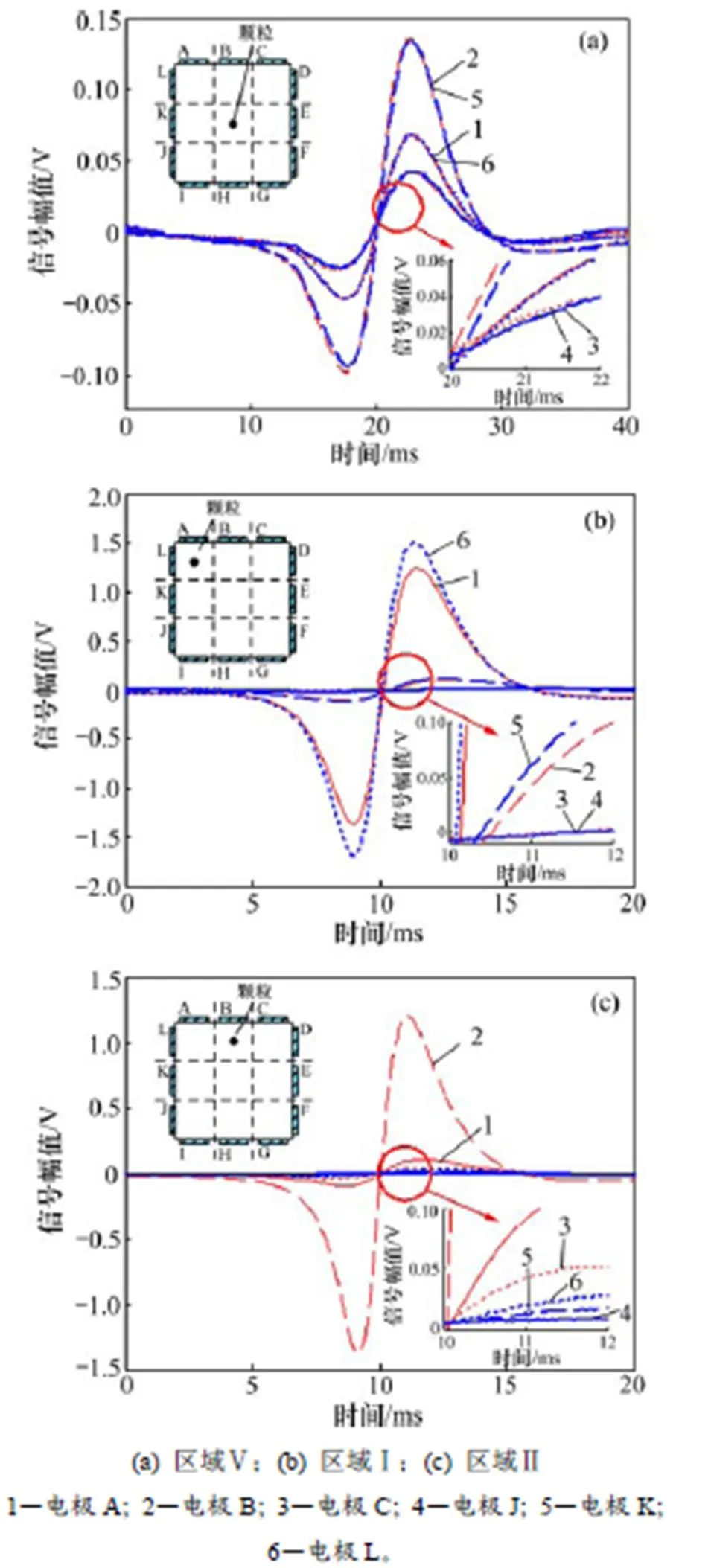
图8 不同区域颗粒激励下静电传感器阵列输出信号
为更好地对比实验结果与仿真数据,选取激励源(颗粒/点电荷)在区域Ⅴ内沿管道中心轴线移动,将图8(a)中电极B的实验结果与图3(b)中同一电极感应电流的仿真结果归一化后进行对比,如图9所示。从图9可以看出:由于实验中不可避免的环境噪声,实验数据波形中含有多个微小波峰;另外,归一化曲线中前半部分实验结果比仿真结果幅值低,存在一定偏差。而后半部分重合度较好,主要是因为实验中颗粒进、出电极敏感空间时电极感应电流输出不完全对称。图9中实验波形的整体变化趋势与仿真波形基本吻合,表明该方形静电传感器阵列感应机理的数学模型有效。

图9 电极B感应电流仿真结果与实验结果对比
4 结论
1) 基于静电学基本理论及镜像电荷法建立的方形静电传感器阵列感应机理模型,可以定量推导出传感器阵列各电极在点电荷激励下的感应电荷、感应电流。传感器输出与电极尺寸及布局、源电荷的电荷性质、电量以及电荷的位置有关。
2) 由分布式条形电极组成的方形静电传感器阵列对传感器管段横截面上电荷的位置信息非常敏感,方形静电传感器阵列可以测量方形管道内气固两相流局部粉体的流动特征。
3) 通过单颗粒重力下落实验,获得方形静电传感器阵列在管道内不同区域单颗粒移动激励下的感应输出,实验结果与仿真结果变化趋势基本吻合,表明建立的解析式数学模型有效。
[1] MILLS D. Pneumatic conveying design guide[M]. 2nd ed. Oxford, UK: Elsevier Butterworth-Heinemann, 2004: 3−28.
[2] LIU Shi, CHEN Qi, WANG Haigang, et al. Electrical capacitance tomography for gas–solids flow measurement for circulating fluidized beds[J]. Flow Measurement and Instrumentation, 2005, 16(2): 135−144.
[3] ZHENG Yingna, LIU Qiang. Review of techniques for the mass flow rate measurement of pneumatically conveyed solids[J]. Measurement, 2011, 44(4): 589−604.
[4] QIAN Xiangchen, YAN Yong, HUANG Xiaobin, et al. Measurement of the mass flow and velocity distributions of pulverized fuel in primary air pipes using electrostatic sensing techniques[J]. IEEE Transactions on Instrumentation and Measurement, 2017, 66(5): 944–952.
[5] 张博, 王陶, 徐立军, 等. 粉料气力输送状态在线监测装置研究[J]. 仪器仪表学报, 2007, 28(11): 1999−2002. ZHANG Bo, WANG Tao, XU Lijun, et al. On-line monitoring of pneumatic conveyance of particulate solids[J]. Chinese Journal of Scientific Instrument, 2007, 28(11): 1999−2002.
[6] WANG Chao, ZHANG Jingyu, ZHENG Wei, et al. Signal decoupling and analysis from inner flush-mounted electrostatic sensor for detecting pneumatic conveying particles[J]. Powder Technology, 2017, 305(1): 197−205.
[7] 高鹤明, 常琦, 晏克俊. 基于阵列式静电传感器的密相气力输送表观气速测量方法研究[J]. 仪器仪表学报, 2015, 36(4): 787−794. GAO Heming, CHANG Qi, YAN Kejun. Research on the superficial gas velocity measurement method of dense-phase pneumatic conveying based on electrostatic sensor array[J]. Chinese Journal of Scientific Instrument, 2015, 36(4): 787−794.
[8] 阚哲, 邵富群. 基于静电传感器气−固两相流质量流率测量[J]. 东北电力大学学报(自然科学版), 2010,31(4): 473−476. KAN Zhe, SHAO Fuqun. Measuring mass flowrate of gas–solid two-phase flow by electrostatic sensors[J]. Journal of Northeastern University (Nature Science), 2010, 31(4): 473–476.
[9] GAJEWSKI J B. Electrostatic nonintrusive method for measuring the electric charge, mass flow rate, and velocity of particulates in the two-phase gas–solid pipe flows–its only or as many as 50 years of historical evolution[J]. IEEE Transactions on Industry Applications, 2008, 44(5):1418−1430.
[10] LAW S E. Electrostatic induction instrumentation for tracking and charge measurement of airborne agricultural particulates[J]. Transactions of the ASAE, 1975, 18(1): 40−45.
[11] GAJEWSKI J B, SZAYNOK A. Charge measurement of dust particles in motion[J]. Journal of Electrostatics, 1981, 10: 229−234.
[12] YAN Yong, BYRNE B, WOODHEAD S, et al. Velocity measurement of pneumatically conveyed solids using electrodynamic sensors[J]. Measurement Science and Technology, 1995, 6(5): 515−537.
[13] XU Chuanlong, WANG Shimin, TANG Guanhua, et al. Sensing characteristics of electrostatic inductive sensor for flow parameters measurement of pneumatically conveyed particles[J]. Journal of Electrostatics, 2007, 65(9): 582−592.
[14] XU Chuanlong, LI Jian, GAO Heming, et al. Investigations into sensing characteristics of electrostatic sensor arrays through computational modelling and practical experimentation[J]. Journal of Electrostatics, 2012, 70(1): 60−71.
[15] KRABICKA J, YAN Yong. Finite-element modeling of electrostatic sensors for the flow measurement of particles in pneumatic pipelines[J]. IEEE Transactions on Instrumentation and Measurement, 2009, 58(8): 2730−2736.
[16] YAO Jun, ZHAO Yanlin, FAIRWEATHER M. Numerical simulation of turbulent flow through a straight square duct[J]. Applied Thermal Engineering, 2015, 91(12): 800−811.
[17] MURNANE S N, BARNES R N, WOODHEAD S R, et al. Electrostatic modelling and measurement of airborne particle concentration[J]. IEEE Transactions on Instrumentation and Measurement, 1996, 45(2): 488−492.
[18] PENG Lihui, ZHANG Yan, YAN Yong. Characterization of electrostatic sensors for flow measurement of particulate solids in square-shaped pneumatic conveying pipelines[J]. Sensor Actuators A: Physical, 2008, 141(1): 59−67.
[19] ZHANG Shuai, QIAN Xiangchen, YAN Yong, et al. Characterisation of pulverised fuel flow in a square-shaped pneumatic conveying pipe using electrostatic sensor arrays[C]// Proceedings of IEEE Instrumentation and Measurement Technology Conference. New York, USA: Institute of Electrical and Electronics Engineers Inc., 2016: 601−605.
[20] GRIFFITHS D J. Introduction to electrodynamics[M]. 4th ed. New Jersey, USA: Addison-Wesley, 2012: 124−126.
[21] 刘尚合, 武占成, 等. 静电放电及危害防护[M]. 北京: 北京邮电大学出版社, 2004: 32−61.LIU Shanghe, WU Zhancheng, et al. Electrostatic discharge and hazard prevention[M]. Beijing: Beijing University of Posts and Telecommunications Press, 2004: 32−61.
(编辑 伍锦花)
Mathematical modeling and experimental evaluation of square-shaped electrostatic sensor arrays for gas–solid two-phase flow measurement
ZHANG Shuai1, YAN Yong1, 2, QIAN Xiangchen1, HU Yonghui1
(1. School of Control and Computer Engineering, North China Electric Power University, Beijing 102206, China; 2. School of Engineering and Digital Arts, University of Kent, Kent CT2 7NT, UK)
To study the sensing mechanism of square-shaped electrostatic sensor arrays that compose of distributed strip-shaped electrodes, a mathematical model was proposed based on electrostatics theory and image method. Through simulating a moving point charge with different moving paths, the induced charge and current of different electrodes in the sensor arrays were derived from the proposed model. A gravity-fed particle flow test rig with a square-shaped pipe section was designed and constructed to evaluate the mathematical model. The square-shaped electrostatic sensor arrays were composed of two layers of strip-shaped electrodes, and 12 (3×4) strip-shaped electrodes were uniformly embedded in four flat pipe walls in each layer. By changing particle’s position across the pipe section, outputs of different electrodes in the sensor arrays were obtained accordingly. The results show that experimental results are in line with simulation results from mathematical model, which indicates that the proposed model is effective in practice.
gas–solid two-phase flow; square-shaped pipe; electrostatic sensor; mathematic modeling; method of images
TP212
A
10.11817/j.issn.1672-7207.2018.03.015
1672−7207(2018)03−0618−08
2017−03−07;
2017−05−13
国家自然科学基金资助项目(61603135) (Project(61603135) supported by the National Natural Science Foundation of China)
钱相臣,博士,副教授,从事多相流检测技术、智能仪表与工业过程状态监测研究;E-mail: xqian@ncepu.edu.cn

