基于混合磨损模型的模具轮廓优化设计

徐戊矫，刘承尚，马欣，郭子乾，陈菲

基于混合磨损模型的模具轮廓优化设计

徐戊矫，刘承尚，马欣，郭子乾，陈菲

(重庆大学 材料科学与工程学院，重庆，400044)

针对成形过程模具的磨损剧烈，模具寿命低的问题，采用混合磨损模型对模具轮廓进行优化设计。以轮毂锻造成形过程中上模芯磨损为例，对上模芯轮廓进行分析，确定待优化的3个设计参数。根据黏着磨损、磨粒磨损及氧化磨损这3个磨损模型建立新磨损计算模型，并通过有限元软件数值模拟获取模具轮廓各处的磨损，以等磨损量作为模具轮廓磨损均匀的评判标准。在此基础上，以有限元软件数值模拟数据作为训练样本，采用BP神经网络建立上模芯轮廓设计参数与模具等磨损量的非线性映射关系。最后，结合训练好的函数映射关系和遗传优化算法，对轮毂锻模的上模芯进行形状优化设计，反求出磨损最均匀状态下的上模芯设计参数。研究结果表明：优化后上模芯等磨损量比优化前减少了29.65%，且最大磨损下降了12.59%，上模芯磨损更均匀且最大磨损量更小。

混合磨损模型；模具轮廓；模具磨损；优化设计

接触压力、滑动速度和模具温度是影响模具磨损的重要因素，研究磨损模型，建立模具接触条件与磨损量之间准确数值关系是减少模具磨损、提高模具寿命的前提。在磨损模型、磨损方程的调研中发现，计算摩擦磨损问题的方程超过300个，描述磨损类型的磨损方程超过180个。以研究者命名的摩擦磨损变量超过600个，而对于基本的滑动磨损形式有近100个变量和参数[1]。这些磨损模型往往针对特定产品、问题适用，目前并不存在适用于所有磨损问题的磨损计算模型。1957年BURWELL[2]根据磨损机制将磨损分为4大基本磨损类型，即黏着磨损、磨粒磨损、疲劳磨损和腐蚀磨损，这些磨损类型是造成机械零件失效的主要原因。大多数钢材随着接触压力、滑动速度以及环境温度等工况条件的变化，其磨损率和摩擦因数会产生变化，并且磨损机理也会不同。SO[3]研究表明，在低接触压力和低滑动速度下，对磨表面的温度较低，此时钢的磨损机理主要为黏着磨损及磨粒磨损，并且摩擦因数较高，磨损率较低。随着压力和速度升高，表面出现了严重氧化，此时的磨损机理主要为氧化磨损，并且摩擦因数大大降低，而磨损量显著增加。BARRAU等[4]研究发现在循环载荷下各种磨损机制的交互作用决定了热锻模具的寿命，如黏着磨损、磨粒磨损和氧化磨损。研究磨损问题，建立准确磨损预测模型是进行磨损分析的关键，然而，考虑到模具磨损模型有各种形式，往往不单独存在，所以，应该根据模具工作实际工况建立磨损模型，得到的模型更符合实际情况。而模具轮廓形状直接影响模具与坯料间的接触压力和滑动速度[5]，是影响模具磨损的一个重要因素。模具轮廓优化的重点和难点在于模具轮廓数学描述以及优化方法的选择。现有的模具轮廓优化方法大多是采用三次样条曲线描述模具轮廓[6−7]，通过有限元模拟建立轮廓与磨损量的BP神经网络，然后采用基于初值优化算法(如二次序列算法)对等磨损量进行寻优[8]。由于机床加工三次样条曲线时，采用编制微小直线段和圆弧逼近，导致编程复杂、效率低、加工精度低[9]。同时，BP神经网络存在自身高度非线性，运用基于初值迭代寻优的传统优化方法极易陷入局部最优，选取不同的初值往往会得到不同结果，影响模具优化效果。而遗传算法在全局范围随机选取多组初值，对所有个体进行并行搜索，保证了优化不会轻易陷入局部最优解，从而搜索到全局最优解。以全局并行搜索方式对群体中的最优个体进行搜索，具有简单方便、鲁棒性强等特点[10]。本文作者选取轮毂锻模上模芯为研究对象，首先，从模具可加工性出发，以简单曲线组合的方式来描述模具轮廓，其可加工性和加工精度可大大提高。然后，从磨损量计算模型出发，建立基于3种基本磨损类型的磨损计算模型，建立模具接触条件与磨损量之间更准确的数值关系。最后，从模具寿命出发，采用训练好的BP神经网络代替有限元模拟，建立模具形状与磨损量的非线性映射关系；结合映射关系和遗传优化算法，对轮毂锻模的上模芯进行形状优化设计。

1 模具优化问题描述

轮毂锻件是典型短轴类锻件，且属于轮毂高突缘大的锻件。对于该类锻件一般使用镦粗制坯。轮毂锻件轴向尺寸较大，既要防止产生折叠，又要保证轮毂成形。径向最大尺寸在轮辐处，很大一部分金属流入飞边槽，很容易造成内端角处金属量不足而充不满。因此，此轮毂件的主要成形难点在于轴向和径向轮辐的充填，为保证尽可能充填饱满，需要采用制坯和终锻成形相结合的工艺流程，并使制坯后的毛坯在终锻时能以镦粗方式成形，本文重点研究轮毂终锻成形工艺部分。

对轮毂锻造工厂失效模具进行观察和分析发现轮毂锻模组件中上模芯的圆角处磨损最为严重，大大地超过了其他部位的磨损，因此，优化的目的是通过优化上模芯的形状来使上模芯处的磨损量变得更均匀，从而提高整个轮毂锻模的使用寿命。

由于轮毂锻件为回转体零件，因此，有限元模型可以简化成如图1所示的二维模型。

首先，分析上模芯轮廓以确定待优化的设计参数，并将设计参数设计为CAD模具模型。其次，导入模具CAD模型，通过有限元软件进行锻造模拟分析，得到应力场、速度场、温度场等工况条件。之后，根据黏着磨损、磨粒磨损及氧化磨损三大磨损模型建立新磨损计算模型，并通过已获得的工况条件作为输入，获取模具轮廓各处的磨损量，以等磨损量作为模具轮廓磨损均匀的评判标准。然后，以有限元软件数值模拟数据作为训练样本，采用BP神经网络建立上模芯轮廓设计参数与模具等磨损量的非线性映射关系。最后，结合映射关系和遗传优化算法对轮毂锻模的上模芯进行形状优化设计，得到磨损最均匀状态下的上模芯设计参数。

图1 轮毂锻造成形有限元模拟

1.1 上模芯轮廓描述

模具轮廓优化的重点和难点之一在于模具轮廓数学描述，描述模具型腔轮廓有多项式函数、分段直线、曲线拟合和曲线插值等。三次样条曲线二阶导数连续，所产生的曲线光滑性高，常用于机翼外形等曲线光滑程度较高部位，大多数文献也运用三次样条曲线进行模具型腔优化设计。考虑到三次样条曲线在机床加工过程中运用微小直线段和圆弧逼近，导致编程复杂、效率低、加工精度低。在加工上模芯的过程中往往用直线和圆弧逼近最为简单方便，无需插补。直线和圆弧表示轮廓形状更加符合实际加工情况，因此用2条线段的斜率1，2和半径描述轮毂上模芯圆角附近轮廓形状。

上模芯轮廓描述以确定待优化的设计参数，将设计参数赋予特定值后进行CAD建模，作为有限元模拟的输入。

1.2 有限元分析

完成CAD建模准备工作后，进入Deform−2D主程序进行CAE模拟，对轮毂锻造成形进行有限元分析之后，在后处理中运用点跟踪的方法获得上模芯9个跟踪点处的接触信息，跟踪点1~9位置如图2所示。

图2 上模芯轮廓形状及其测试点位置

以靠近圆角附近的第4号跟踪点为例，其速度、温度和应力等接触条件如图3所示。

图3 轮毂锻造成形上模芯4号跟踪点接触条件

1.3 磨损模型建立

通过锻造成形模拟已获得模具轮廓各处的速度、温度和应力等接触条件，建立模具接触条件与磨损量之间准确数值关系是为后期改善模具磨损，提高模具寿命的前提。

轮毂锻模上模芯的材料为H13钢，模具在工作过程中发生的磨损类型往往不单一存在。陈康敏等[11]研究发现H13钢在磨损过程中主要的磨损机理为黏着磨损、磨粒磨损和氧化磨损。

黏着磨损也叫做摩擦磨损或胶合磨损，由于模具表面与工件均凹凸不平，发生相对运动时，其中一些接触点所受到的应力将超出材料的屈服点而发生塑性变形进而产生黏着，由于剪切断裂易发生在这种黏着效应所形成的结点上，从而导致模具接触表面的材料产生转移或者发生脱落，这种现象叫黏着磨损。

图4 黏着磨损模型示意图

材料发生黏着磨损的磨损深度可以表示为

式中：为磨损系数；为接触面上的正压力(法向应力)；为2个接触表面相对滑动速度；为材料的硬度；为2个接触表面滑动时间。

由于模具和工件间存在外来的硬质颗粒，或者工件表面本身存在硬质凸起物、颗粒，它们的存在造成模具表面被刮伤、有犁沟和划痕出现，从而导致磨粒磨损。

图5 磨粒磨损模型示意图

材料发生磨粒磨损的磨损深度可以表示为

QUINN[12]研究证实，对于2个相互滑动的表面，由于外部加热以及摩擦时产生的热量，磨损表面会发生氧化并在接触表面会出现较厚的片状氧化层，该氧化层将参与摩擦磨损过程，对磨损表面形成物理隔离，氧化层的形成和剥落引起氧化磨损。

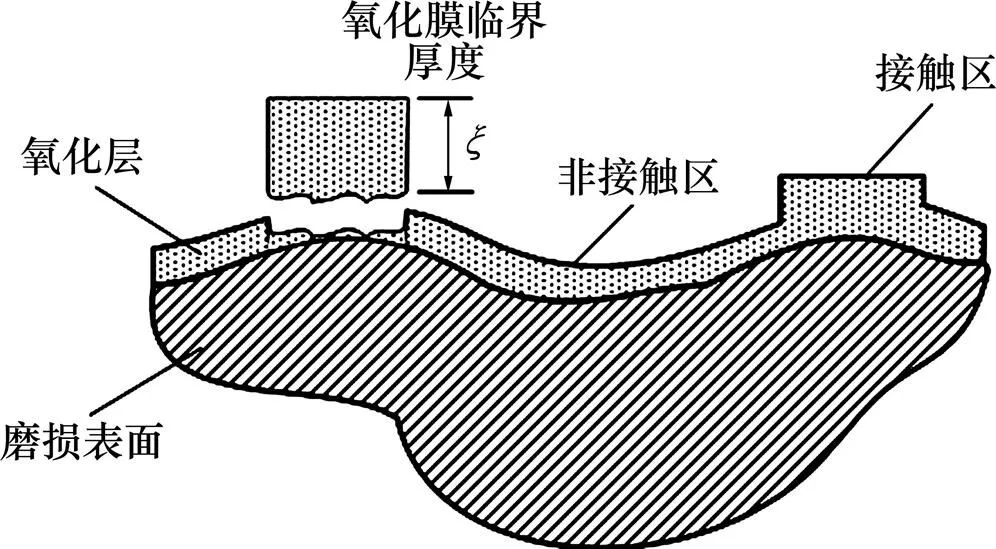
图6 氧化磨损模型示意图

材料发生氧化磨损的磨损深度可以表示为

式中：p为抛物线型氧化Arrhenius常数；p为抛物线型氧化激活能；为与磨损表面上氧化物Fe3O4和Fe2O3所占比例有关的参数；变量p，p和可以根据文献[12]获得。该表达式说明材料的磨损率与自身的氧化性能直接相关。

为了表示一次锻造过程中模具的总磨损量，并显示不同类型磨损在总量中所具有的重要程度，分别给予不同磨损类型不同的权重系数，该磨损类型对应的权重系数表示该磨损类型所占的比例。依据这3种单磨损模型建立新磨损计算模型如下：

表1 各种磨损类型磨屑特征

可通过MATLAB图像处理功能，使用特定的磨粒图像的预处理方法和磨粒形态特征的提取方法，按照表1，对3种磨屑进行分类并计算各类磨屑所占比例。首先，对磨屑扫描图片进行滤波、去噪等预处理，并设置灰度阈值将所有磨屑与黑色背景分割开，如图7(b)所示；然后提取出所有磨屑的形态特征量(圆形度、细长度和凹度)，并将形态特征量作为分类器的输入，对分割好的所有磨屑进行分类，磨屑分类结果如图7(c)所示。

图7 扫描电镜图片处理结果

选取整体磨屑的4个视野区域，采用扫描电镜对各区域进行观察，分别统计各区域3种磨屑类型所占比例，即黏着磨损、磨粒磨损和氧化磨损类型所占权重，最后取其平均值作为磨损模型的权重系数。

1.4 优化目标建立

由磨屑的扫描电镜图片确定新磨损模型，然后将新磨损模型导入DEFORM计算上模芯所有测试点处的磨损。

表2所示为在一次锻造后第4号跟踪点所有模拟步有关参数值以及锻造成形后总磨损量。从表2可以看出：利用权重系数的磨损模型计算到的磨损量比黏着模型计算到的磨损量大近1个数量级。

磨粒磨损可以表示为类似黏着磨损的计算式。其中，abr包括微凸体几何形状和给定微凸体的剪切概率，是量纲为一的磨损系数，abr的取值范围在10−6~10−1之间，磨粒磨损率一般非常大，比黏着磨损率大2~3个数量级。因此，综合考虑3种磨损情况的新模型获得的磨损量一般比单一考虑黏着磨损模型的大1~2个数量级。

等磨损量作为衡量模具磨损的均匀程度的指 标[8]，其计算模型如下：

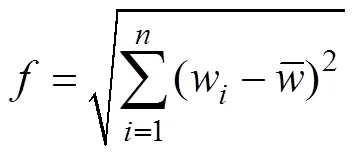
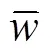
为了避免上模芯局部累计磨损量过大，使上模芯圆角处的磨损更均匀，等磨损量应当越小越好。

试验时，采用L9(34)三水平四因素正交设计，考察设计变量斜率1，斜率2，圆角半径，留出一列作为误差列。为了避免人为因素导致的系统误差，因素的各水平按着“随机化”的方法处理。最终的正交试验方案和结果如表3所示。

表2 第4号跟踪点锻造模拟时对应的磨损量

表3 试验方案与试验结果

对正交试验结果进行简单极差分析，得到优方案B1A2C3，表示设计条件为：斜率1=0，斜率2=11.430，圆角半径=3 mm。

2 模具形状优化

2.1 网络结构

在上模芯形状优化中，根据设计变量建立起上模芯的2D模型，目标函数(等磨损)的获得通常是进行有限元数值方法计算得到的。然而，在进行优化过程中，如果每一组设计量都进行一次有限元计算分析，这样优化所需时间将难以接受，甚至根本无法进行优化。神经网络模型代替有限元计算可以很好地解决这个问题，将优化过程中大量的有限元计算转化为训练试验样本的计算和神经网络模型的建立，将大大减少了优化的时间[15]。

BP神经网络由输入层、隐含层和输出层3个部分组成，层与层之间采用不同的连接函数来进行连接。研究表明，由1个输入层、1个隐含层和1个输出层组成的三层BP神经网络能够以任意精度逼近任意非线性问题[16]。因此，使用三层BP神经网络来表示1，2和之间的内在规律。网络输入层为3个决定模具形状的设计参数，网络输出层为等磨损模型计算值，隐层神经元数目可由下式得到：

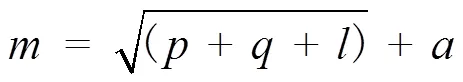
其中：为隐层神经元数目；为输入层神经元数目；为输出层神经元数目；为1~10之间的常数。

经过调试隐层数目最终确定为8个神经元，输入层和隐含层采用双曲正切S型tansig函数连接，隐含层和输出层采用线性purelin函数连接，建立的BP神经网络结构如图8所示。

图8 BP神经网络结构

2.2 网络训练和测试

正交试验设计法具有均衡分散性和整齐可比性，这保证了样本的代表性，大大减少了学习样本结构分析的时间。

表3中9个正交实验样本集被用于训练所设计的神经网络。BP神经网络训练时的参数设置如下：网络学习速率为10−6，训练数据的均方误差为10−8，最大训练次数为100次。随着训练次数的增加和连接权重的不断更新，神经网络预测出的数据与训练数据之间的均方误差逐渐降低并且在训练次数为34次时达到10−12，此时神经网络收敛。

本文选取5个区别于训练样本的测试样本来测试训练好的神经网络的精度和可靠性，测试结果如图9所示。神经网络预测的测试结果与测试样本数据具有良好的一致性，各点相对误差均小于5.0%。因此，训练好的BP神经网络能够较好地反映设计变量与目标函数之间的映射关系，可以作为后续优化的知识源。

图9 神经网络预测值与期望值对比

2.3 遗传算法模具形状优化

基于BP神经网络，获得了设计参数1，2，与其对应的等磨损量之间的映射关系。然后，运用遗传算法来获得等磨损量最小时(磨损最均匀)对应的轮毂锻模上模芯的形状。遗传算法是一种自适应全局优化概率搜索算法。由于其简单、通用、不依赖问题模型的特性，适合并行分布处理，已广泛地应用到诸多领域[17]。

优化过程中寻找适应度最小的个体，即得到模具等磨损量最小时所对应的模具型腔。寻优结束后，得到最优的模具型腔形状的设计参数为斜率1=0，斜率2=6.612，圆角半径=2.7 mm。对比极差分析的最优结果1=0，斜率2=11.430，圆角半径3 mm，可以看出基于神经网络遗传算法寻优与极差分析寻找的最优设计参数具有较好一致性。但是，基于神经网络遗传算法寻优的能力更强，它不仅可以对离散数据点进行寻优，而且可以对设计参数3水平以外的设计参数进行寻优，只要求待优化的参数与优化目标值之间建立一种映射关系即可。

设计参数用2条线段的斜率1，2和半径描述轮毂上模芯圆角附近轮廓形状，将寻优后参数输入即可得到最终优化后模芯轮廓形状尺寸，如图10所示。将优化前后的轮毂锻模上模芯轮廓导入DEFORM进行数值计算，其结果如图11所示。

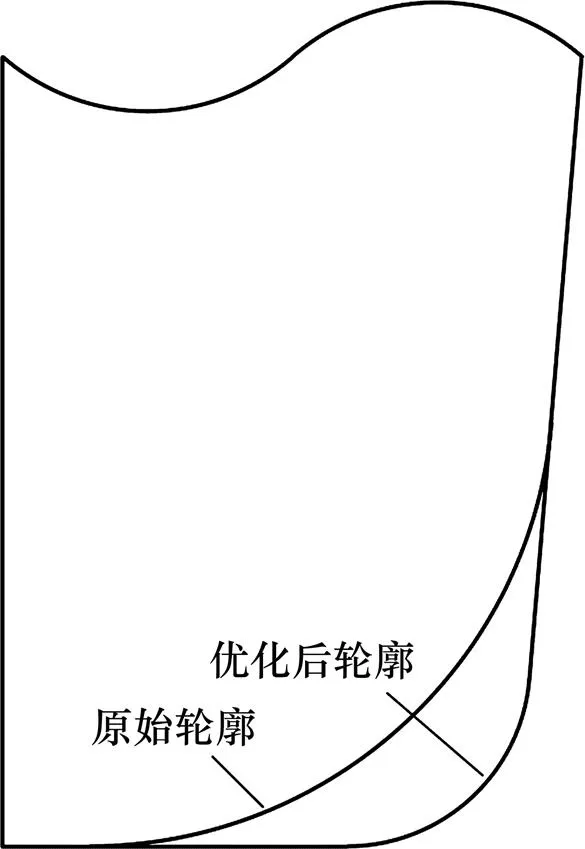
图10 初始轮毂锻模上模芯形状和优化之后形状对比

上模芯9个测试点优化前后磨损量对比情况如图12所示。从图12可见：优化后的上模芯等磨损量和最大磨损量比优化前有很大的降低，优化前后的等磨损量分别为2.172×10−4 mm和1.528×10−4 mm，最大磨损量分别为1.975×10−4 mm和2.259×10−4 mm。通过使用遗传算法来对轮毂锻模上模芯的形状进行优化，优化后上模芯的等磨损量比优化前的减少了29.65%，且最大磨损量下降了12.59%。

2.4 优化结果分析

针对轮毂锻模上模芯的优化结果，在MGW−02高速往复摩擦磨损试验仪上进行磨损试验验证。试验机的外观及磨损试验原理示意图如图13所示。H13钢磨损试样的制备工艺为：将H13钢板材用线切割的方法切割成直径×长度为20 mm×3 mm的底板试样。45钢对磨试样的制备工艺为锯切下料，采用精车的方法将45钢棒料加工成对磨压头。

使用MGW−02高速往复摩擦磨损试验仪自带磨损深度测量设备测量磨损试样在磨损后的磨损深度，测量3次取其平均值作为该磨损试样的磨损量。

图11 优化前后轮毂锻模上模芯磨损情况对比

图12 有限元模拟优化前后磨损量对比

第4号跟踪点的速度、温度和应力接触条件如图3所示。从图3可以看出接触条件在整个锻造成形过程中是不断变化的。然而，摩擦磨损试验机在运行时不可以实时地改变其接触条件，因此，在运用MGW−02高速往复摩擦磨损试验仪进行磨损试验之前，根据整个锻造成形过程中轮毂锻模上模芯4号跟踪点处应力的变化规律，近似地将其划分3阶段，滑动速度以及温度也使用同样的方法进行划分。

此轮毂锻模的寿命为4 000件左右，而单次锻造成形过程中阶段1、阶段2、阶段3用时分别为 0.303，0.027和0.048 s，所以，在模具整个的服役期间阶段1、阶段2、阶段3用时分别为20.2，1.8和3.2 min。最终确定的磨损试验条件如表4所示。

图13 摩擦磨损试验仪及磨损试验原理示意图

表4 磨损试验条件

磨损试验后的磨损试样如图14所示，用电子扫描显微镜(TESCAN VEGA3 LMH型)对磨屑的形貌进行观察和分析。通过MATLAB图像处理功能，使用专业的磨粒图像的预处理方法和磨粒形态特征的提取方法，提取出各形态特征量作为分类器的输入。根据表1中3种主要磨屑的磨损特征，将整体的磨屑与背景区分开，并对区分开的磨屑进行分类。

图14 优化后磨损试验结果

根据磨屑特征计算得到新磨损模型式(4)机理权重系数，并基于新磨损计算模型，可以计算出优化后的上模芯各测试点处的磨损深度。最后，运用式(5)可以得到上模芯优化后的等磨损量。

上模芯优化前后磨损情况对比如图15所示。从图15可知：试验时测得的磨损量与磨损深度的计算值具有良好的一致性。因此，建立的基于权重体系的新磨损模型具有较高的精度。比较优化前后上模芯的等磨损量和最大磨损量，不仅磨损更加均匀，而且最大磨损量有明显降低。

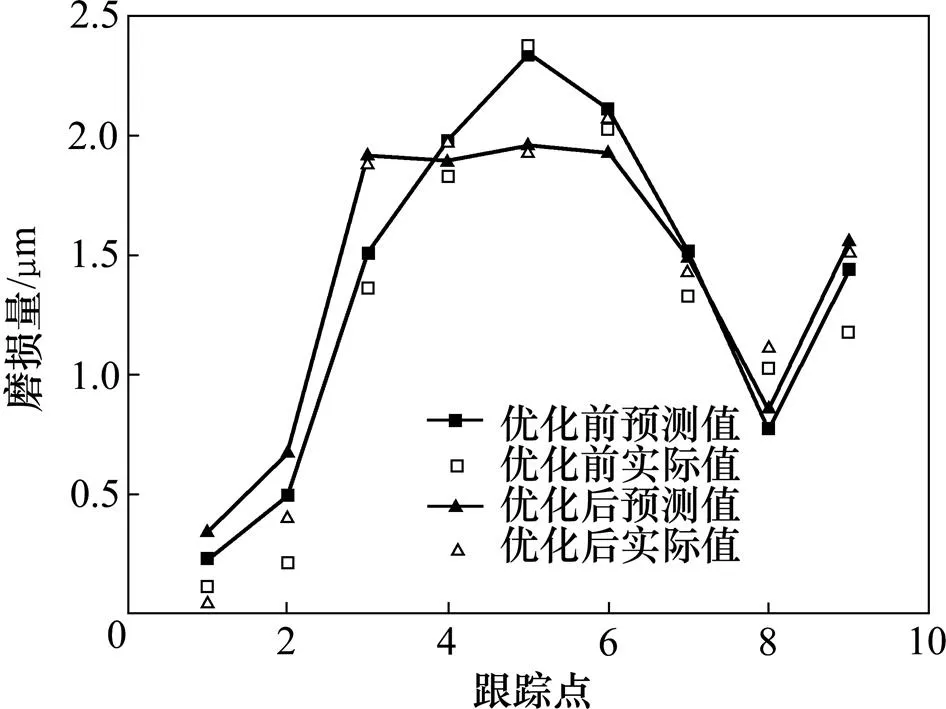
图15 上模芯优化前后磨损情况对比

3 结论

1) 采用三因素设计变量(斜率1，斜率2，圆角半径)可以较充分描述轮毂锻模上模芯轮廓形状，既精简描述参数，又不损失重要信息。

2) 比较原始黏着磨损模型、新磨损模型计算得到的磨损量与摩擦磨损试验得到的磨损量，新模型计算得到的磨损量与试验获得的磨损量更接近。

3) 正交试验设计保证样本的代表性，并通过神经网络建立了设计变量与目标函数(等磨损量)之间的映射关系。使用遗传算法获得了等磨损量最小(磨损最均匀)时，所对应的轮毂锻模上模芯的形状。优化后的上模芯比优化前磨损更均匀，且最大磨损量更小。

[1] 温诗铸. 材料磨损研究的进展与思考[J]. 摩擦学学报, 2008, 28(1): 1−3. WEN Shizhu. Research progress on wear of materials[J]. Tribology, 2008, 28(1): 1−3.

[2] BURWELL J T. A survey of possible wear mechanism[J]. Wear, 1957, 1(2): 119−141.

[3] SO H. The mechanism of oxidational wear[J]. Wear, 1995, 184(2): 161−167.

[4] BARRAU O, BOHER C, GRAS R, et al. Wear mechanisms and wear rate in a high temperature dry friction of AISI H11 tool steel: Influence of debris circulation[J]. Wear, 2007, 263(1/2/3/ 4/5/6): 160−168.

[5] XU Wujiao, LI Wuhua, WANG Yusong. Experimental and theoretical analysis of wear mechanism in hot-forging die and optimal design of die geometry[J]. Wear, 2014, 318(1/2): 78−88.

[6] ZOU Lin, XIA Juchen, WANG Xinyun, et al. Optimization of die profile for improving die life in the hot extrusion process[J]. Journal of Materials Processing Technology, 2003, 142(3): 659−664.

[7] 孙宪萍, 王雷刚, 黄瑶, 等. 挤压模具型腔的等磨损优化设计[J]. 润滑与密封, 2007, 32(1): 56−59.SUN Xianping, WANG Leigang, HUANG Yao, et al. Uniform wearing optimum design of extrusion die profile[J]. Lubrication Engineering, 2007, 32(1): 56−59.

[8] 黄瑶, 孙宪萍, 王雷刚, 等. 基于BP神经网络的挤压模具磨损预测[J]. 塑性工程学报, 2006, 13(2): 64−66. HUANG Yao, SUN Xianping, WANG Leigang, et al. Wear prediction of extrusion die based on BP neural networks[J]. Journal of Plasticity Engineering, 2006, 13(2): 64−66.

[9] 何晶昌, 夏铭, 黄志勇. 三次样条曲线回转面的车削加工[J]. 组合机床与自动化加工技术, 2011, 12(4): 95−97. HE Jingchang, XIA Ming. HUANG Zhiyong. The turning methods of the revolving surface formed by cubic NURBS curve[J]. Modular Machine Tool & Automatic Manufacturing Technique. 2011, 12(4): 95−97.

[10] 边霞, 米良. 遗传算法理论及其应用研究进展[J]. 计算机应用研究, 2010, 27(7): 2426−2429. BIAN Xia, MI Liang. The theory of genetic algorithm and its research progress in application[J]. Application Research of Computers, 2010, 27(7): 2426−2429.

[11] 陈康敏, 王兰, 王树奇, 等. H13钢氧化磨损行为的研究[J]. 摩擦学学报, 2011, 31(4): 317−322. CHEN Kangmin, WANG Lan, WANG Shuqi, et al. Oxidative wear behavior of H13 steel[J]. Tribology, 2011, 31(4): 317−322.

[12] QUINN T F J. The oxidational wear of low alloy steels[J]. Tribology International, 2002, 35: 691−715.

[13] 袁成清, 严新平. 磨粒类型识别研究[J]. 润滑与密封, 2007, 32(3): 21−24. YUAN Chengqing, YAN Xinping. Study on recognition of types of wear debris[J]. Lubrication Engineering, 2007, 32(3): 21−24.

[14] 陈为平, 高诚辉, 任志英磨粒表征研究进展及发展趋势[J]. 中国工程机械学报, 2015, 13(4): 283−289. CHEN Weiping, GAO Chenghui. Advances and trends on abrasive particle characterization[J]. Chinese Journal of Constructive Machinery, 2015, 13(4): 283−289.

[15] 傅立军, 包忠诩, 陈泽中, 等. 正交试验法、神经网络和遗传算法的结合[J]. 南昌大学学报(工科版), 2003, 25(1): 79−82. FU Lijun, BAO Zhongxu. CHEN Zezhong, et al. Combination of orthogonal experimental method, neural networks and genetic algorithms[J]. Journal of Nanchang University(Engineering & Technology), 2003, 25(1): 79−82.

[16] VENKATA RAO K, MURTHY B S N, MOHAN RAO N. Prediction of cutting tool wear, surface roughness and vibration of work piece in boring of AISI 316 steel with artificial neural network[J]. Measurement, 2014, 51(1): 63−70.

[17] LI Ge. Procedure neural networks based on being learned by hybrid genetic algorithm[J]. Journal of Harbin Institute of Technology, 2005, 37(7): 986−988.

(编辑 赵俊)

Optimum design of die profile based on mixed wear model

XU Wujiao, LIU Chengshang, MA Xin, GUO Ziqian, CHEN Fei

(College of Material Science and Engineering, Chongqing University, Chongqing 400044, China)

Aiming at solving problems of great wearing and low life of mold, the optimum design of die profile based on mixed wear models was used. As an example, the mandrel of wheel hub in forging process was studied, and the contour of mandrel was analyzed in order to select three parameters to optimize. Combined with three basic wear models, i.e., adhesive wear, abrasive wear and oxidative wear, a new calculate model was established, and then wear value of the mold surface was obtained by forging numerical simulation and using uniformity wear which can reflect homogeneous degree of wear as judgment standard. On the basis of this analysis, the numerical simulation results were used as training sample to establish three layers BP neural network, and instead of the finite element model with trained BP neural network, the nonlinear mapping relationship between the design variable and the target function was acquired. Finally, combining the trained mapping function and genetic optimization algorithm, the mandrel shape of wheel hub and reverse parameters were optimized under the condition of the most uniform. The results show that after optimization of mandrel, uniformity wear value decreases by 29.65% and maximum wear value reduces by 12.59% than that before optimization, the amount of wear on upper punch becomes more uniform and the maximum wear is smaller.

mixed wear model; mold contour; die wear; optimum design

TG315.2；TH117.1

A

10.11817/j.issn.1672-7207.2018.03.005

1672−7207(2018)03−0544−09

2017−03−30；

2017−05−27

中央高校基本科研业务费资助项目(CDJZR14130005, CDJZR13130087) (Projects(CDJZR14130005, CDJZR13130087) supported by the Fundamental Research Funds for the Central Universities)

徐戊矫，博士，教授，从事材料成形过程数值模拟仿真与优化的研究；E-mail: xuwujiao_cq@163.com