加速工况下圆柱滚子轴承运动特性
曹伟,王家序, 2,蒲伟,周广武,张莹,吴继强,任思
加速工况下圆柱滚子轴承运动特性
曹伟1,王家序1, 2,蒲伟1,周广武1,张莹3,吴继强1,任思1
(1. 四川大学 空天科学与工程学院,四川 成都,610065; 2. 重庆大学 机械传动国家重点实验室,重庆,400044; 3. 四川大学 制造科学与工程学院,四川 成都,610065)
为了准确分析加速过程中圆柱滚子轴承的运动特性,建立圆柱滚子轴承动力学模型,模型中考虑加速度、运行工况、结构参数以及润滑剂流变特性等参数,对轴承运动特性进行瞬态以及时变分析。研究结果表明:考虑润滑剂的黏弹性可以提高动力学模型的预测精度。加速度对轴承打滑影响较大,尤其对非承载区滚子的转速影响较大;加速度越大,轴承滚子和保持架打滑越严重;轴承在加速过程中,滚子转速随时间呈阶梯上升,而保持架转速呈线性增大;滚子由承载区进入非承载区时,滚子转速先略微减小,由非承载区进入承载区时,滚子转速骤然增大;滚子与内滚道间相对滑动速度ij大于滚子与外滚道间的相对滑动速度oj,由于加速度的影响,相对滑动速度oj的方向在最大承载区附近发生变化;在非承载区,滚子与内滚道相对滑动速度较大,大载荷以及小轴承游隙可以有效减小相对滑动速度。
轴承打滑;轴承加速度;圆柱滚子轴承;流变特性
在理想状态下,轴承滚子与滚道间的运动为纯滚动关系,由于滚子离心力和轴承滚道与滚子间摩擦力的影响,以及滚子在承载区与非承载区交替运行,滚子与滚道间会出现滑动,即打滑。轴承在非稳态下运行时,由于加速度的存在,轴承滚子与滚道间的滑动加剧。滚子与滚道间打滑可能造成滚子与滚道表面磨损,因此,研究轴承非稳态下的动力学模型对轴承打滑控制以及轴承接触特性分析具有重要意义。HARRIS[1]提出了可以预测轴承打滑的动力学模型,分析了稳态下载荷对轴承打滑率的影响,同时进行了实验研究,验证了理论模型结果与实验结果在趋势上能较好地吻合。但Harris模型中采用牛顿流体计算摩擦力,且采用了简化计算方法,不能模拟全滚子动态特性以及加速度下的运动特性。CHANG等[2]基于弹性流体动力润滑理论研究了轴承载荷分布以及轴承在稳态运行下的打滑特性。POPLAWSKI等[3]建立了考虑保持架与滚子摩擦力以及搅油损失的滚子轴承动力学模型,金海善等[4]采用改进的牛顿−拉夫逊法研究了考虑油气阻力的轴承打滑特性,陈渭等[5]基于轴承涡动轨迹假设基础,建立了涡动工况下的轴承滚动体运动学及动力学模型。POPLAWSKI等[3−5]建立了全滚子动力学模型,但滚子与滚道间摩擦力计算采用牛顿流体,未考虑润滑剂的粘弹性的影响,同时未分析加速度对轴承动态特性的影响。TU等[6]研究了加速度对轴承打滑的影响,但计算滚子与滚道间的牵引力时未考虑润滑剂的影响。CAO等[7]基于Harris模型研究了加速度对轴承打滑的影响,并分析了加速度对最大承载滚子润滑特性的影响。但模型中摩擦力计算采用DOWSON等[8]基于牛顿流体提出的摩擦力计算公式。文献[9−12]基于弹流润滑研究了稳态下圆柱滚子轴承的动态特性。弹流润滑中理想摩擦力计算采用的流变模型为Newton流体模型,Newton流体模型能够很好地模拟低压以及低滑动速度下的剪切特性。在高压力高剪切率条件下,流体应力和应变不再呈线性关系,实际总应变为黏性剪切应变和弹性剪应变之和[13]。JOHNSON等[14]提出了考虑流体弹性和黏性剪切的非Newton流变模型(J−T模型),BAIR等[15]也提出了指数函数关系的流变模型(B−W模型)。J−T模型和B−W模型的理论计算值与实验测试值具有很好的一致性。为了分析轴承加速过程中圆柱滚子轴承的运动特性,本文作者建立综合考虑轴承结构参数、加速度、润滑剂流变特性等参数的全滚子动力学模型。模型中采用B−W流变模型[15]计算滚子与滚道间的牵引力,并将数值结果与实验结果进行了对比。基于动力学模型研究了加速度、载荷以及轴承间隙等参数对轴承滚子与保持架瞬态转速以及动态特性的影响。
1 动力学模型建立
1.1 运动关系
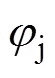

图1 圆柱滚子轴承示意图
理想状态下时,滚子与滚道间为纯滚动。实际工作中,保持架和滚子的转速均小于理论速度,即滚子与滚道间的滑动速度不为0。以滚子为参照坐标系时,滚子与内外滚道间相对滑动速度分别定义为:

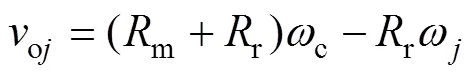
滚子与内外滚道间卷吸速度分别定义为:
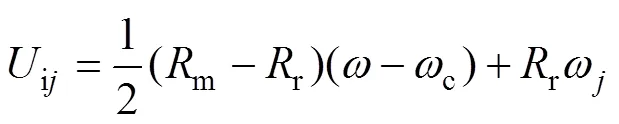

滑动速度和卷吸速度量纲一形式表示为[1]:

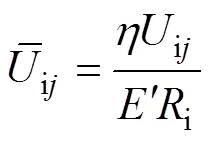
1.2 受力分析
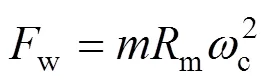


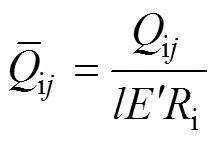
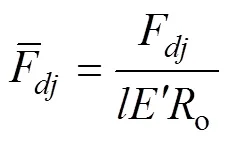
式中:l为滚子与滚道间的有效接触长度。
滚子与滚道间法向力通过载荷平衡方程和协调变形方程来计算,载荷平衡方程和变形协调方程分别 为[16]:
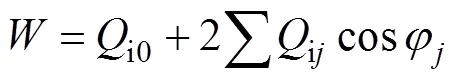


Harris模型中采用Dowson给出的计算公式计算润滑油作用于滚子中心轴的流体动压力,表达式如 下[1]:


本文采用BAIR和WINER提出的非线性黏弹性性流变模型来计算滚子与滚道间的牵引力[11],B−W模型为:
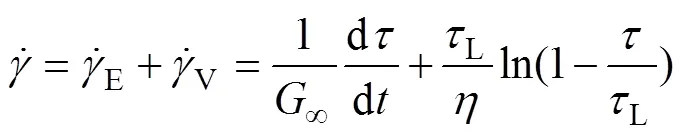
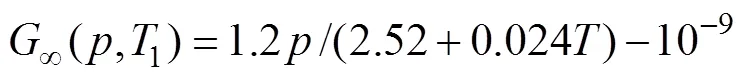

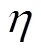

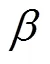
求解方程(15)可得剪切应力,对剪切应力在赫兹接触区积分可得摩擦力:

1.3 动力学模型
由图2可知,对滚子与滚道在接触法向以及切向受力分析可得:
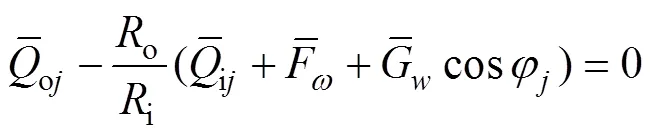
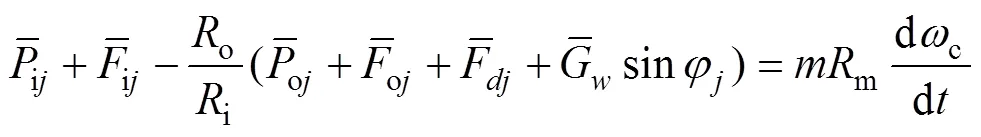
保持架与滚子间存在法向作用力,法向力产生的转矩推动保持架运动,则有

将式(21)代入式(22)可得


同理,滚子绕自身轴线有力矩平衡:


2 计算结果
轴承参数如表1所示,润滑油参数如表2所示。
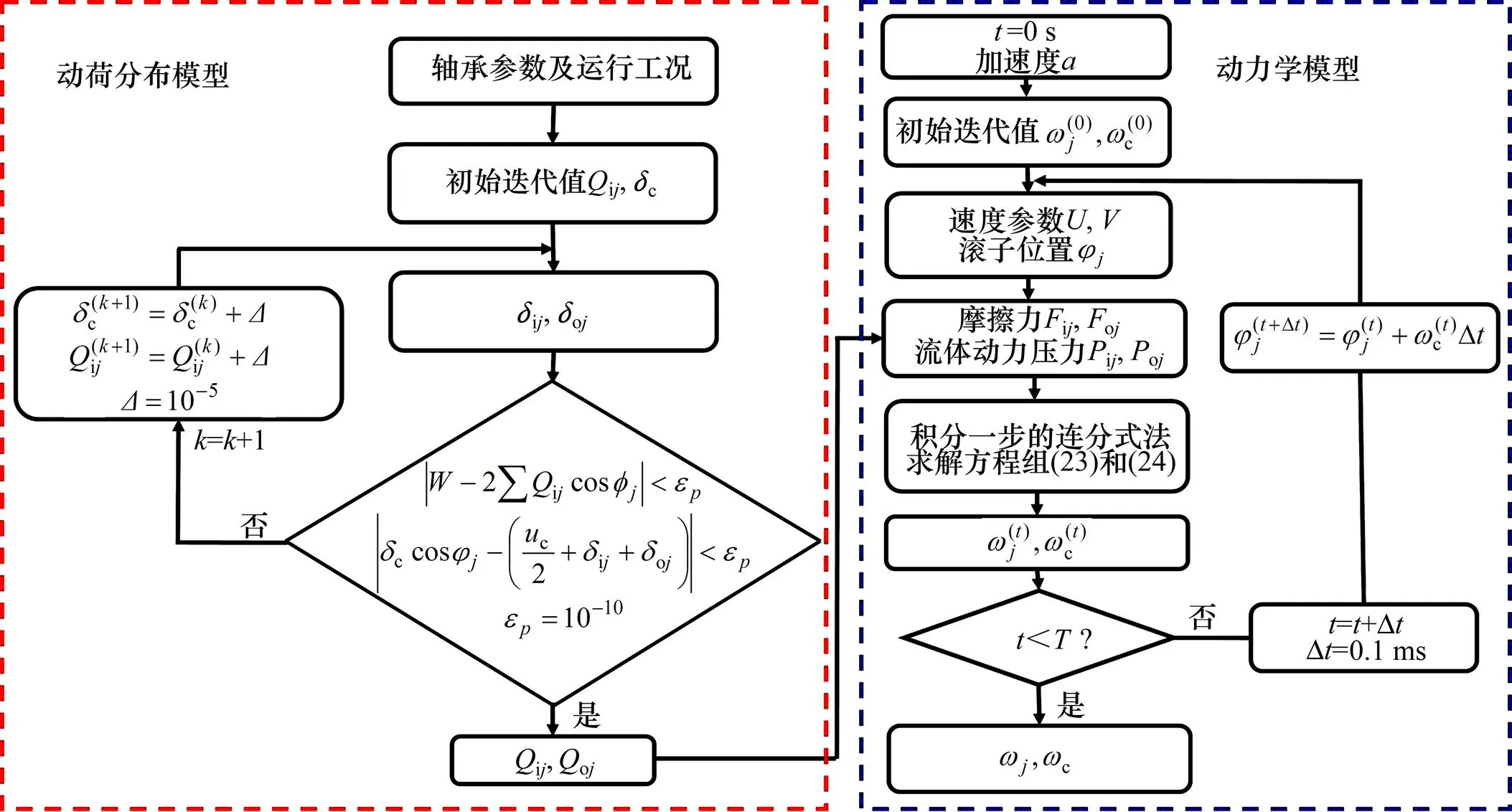
图3 动力学模型计算流程

表1 圆柱滚子轴承参数

表2 润滑油参数
2.1 载荷分布
图4和图5所示分别为载荷和轴承游隙对轴承载荷分布的影响。由图4和5可知:随着轴承载荷增大,最大滚子载荷增大,承载区域增大;轴承游隙对轴承载荷分布影响较大,随着轴承游隙减小,轴承最大滚子载荷减小,承载区增大。

图4 不同载荷下轴承滚子载荷分布

图5 不游隙下轴承滚子载荷分布
2.2 模型验证
为了验证考虑润滑剂黏弹性的全滚子动力学模型的正确性,将本文的动力学模型的数值结果与实验结果进行对比。图6(a)所示为Harris模型的理论计算结果以及实验结果,Harris理论计算采用了简化方程,摩擦力计算采用牛顿流体计算。由图6可知,Harris模型的理论计算值在转速较低时与试验值较吻合,在转速为5 000 r/min时,理论计算值与试验测试值误差较大,且随着载荷降低误差变大。图6(b)所示为采用B−W模型得到的保持架转速随载荷变化。由图6(b)可知:在转速为5 000 r/min时,采用非牛顿流体计算摩擦力时,保持架理论计算值与实验值较吻合。因此,考虑润滑油的黏弹性可以提高轴承动力学模型的打滑预测精度。

图6 不同载荷和内滚道转速下保持架转速随载荷变化
2.3 运动特性分析
为了研究轴承全滚子的动态特性以及滚子在不同运动角位置的动态特性,需要对轴承滚子进行编号说明,滚子编号如图7所示。图8所示为轴承在不同加速度下,轴承载荷为=2 kN,内圈转速达到3 000 r/min(=0.6 s)时,不同位置滚子的转速。轴承纯滚动状态下时,不同位置的滚子转速相同。由图8可知:加速度越大,滚子的实际转速与纯滚动状态转速相差越大,即打滑越严重。在稳态下运行时(加速度为 0 rad/s2),承载区与非承载区滚子转速相差不大,随着加速度增大,滚子在承载区与非承载区的转速相差较大。由于承载区滚子载荷较大,加速度对滚子转速的影响相对于非承载区较小。
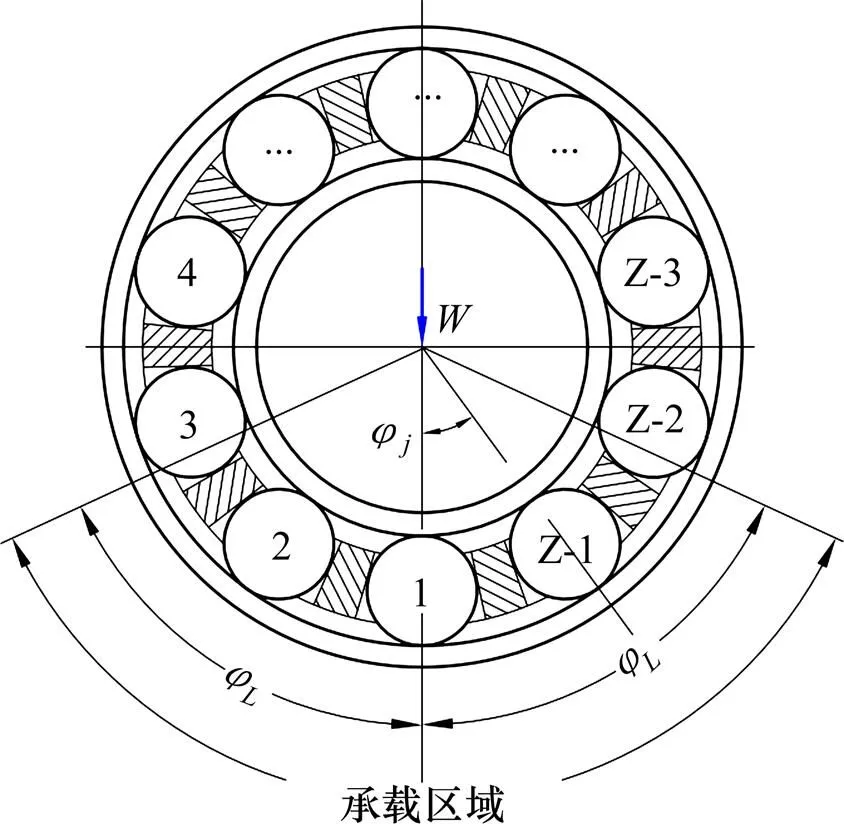
图7 不同位置滚子编号

图8 不同加速度下滚子瞬态转速(ω=3 000 r/min)
由图9可知:轴承加速过程中,滚子转速随时间呈阶梯上升。这是由于承载区与非承载区牵引力的变化导致滚子在承载区打滑较弱,在非承载区打滑相对较严重。保持架转速随时间呈线性增大,加速度越大,保持架转速与纯滚动状态下的转速相差较大。图10和图11所示分别为载荷和轴承游隙对滚子以及保持架转速的影响。由图10可知:当载荷较大时,轴承滚子和保持架转速较接近纯滚动下转速。这是由于载荷增大时,轴承承载区以及滚子与滚道间牵引力增大。由图11可知:当轴承游隙减小时,保持架与滚子转速增大。这是由于当轴承间隙减小时,承载区增大,承载滚子数增多,导致打滑程度减弱。
由图9~11可知:轴承在加速过程中,滚子旋转1周时,由于要经历承载区和非承载区,因此,滚子转速随时间呈阶梯状变化。图12所示为不同载荷以及轴承游隙时,滚子转速在承载区与非承载区随时间的变化情况,此时加速度=523.6 rad/s2。由图12可知:当载荷为4 kN,轴承游隙为0.01 mm时承载区较大。在不同工况下,滚子公转速度(保持架转速)不同,因此,3种工况下滚子在不同时刻进入承载区。当滚子进入非承载区时,滚子转速先略有减小然后再增大,这是由于滚子由承载区进入非承载区时,滚子与内圈的接触力为0,且滚子重力为阻力,导致滚子转速稍微减小;随着内圈转速增大,保持架推动非承载区滚子转速继续增大。当滚子由非承载区进入承载区时,滚子与滚道间牵引力增大,滚子转速骤然增大。

图9 加速度对滚子和保持架转速的影响(W=2 kN)

图10 轴承载荷对滚子和保持架转速影响

图11 轴承游隙对滚子和保持架转速影响

图12 承载区与非承载区滚子转速度变化情况
图13(a)所示为内外滚道间的相对滑动速度ij和oj。由图13(a)可知:滚子与外滚道间的相对滑动速度小于滚子与内滚道间的相对滑动速度。由于加速度的存在,滚子在非承载区和非承载的自转速度变化较大,滚子与外滚道间的相对滑动速度在最大承载位置附近出现正负值交替的现象,即滚子与滚道间的相对滑动速度方向发生变化。图13(b)所示为滚子与内滚道间的相对滑动速度在不同载荷以及游隙时随时间的变化情况。由图13(b)可知:在0.4~0.5 s时间段内,当轴承载荷为2 kN (c=0.05 mm)时,承载区最小滑动速度为0.62 m/s,非承载区的最大滑动速度为1.35 m/s。可知,滚子由承载区进入非承载区时,滚子与滚道间的相对滑动加剧,容易造成滚子与滚道间接触失效。对比3种工况参数下的数值结果可知:大载荷以及小轴承游隙可以减小滚子与滚道间的相对滑动速度。

图13 滚子与内外滚道间相对滑动速度
3 结论
1) 考虑润滑剂流变特性的动力学模型可以提高轴承动态特性的预测精度。
2) 建立的轴承动力学模型可以模拟轴承在不同运行工况下的运动特性。随着加速度增大,滚子以及保持架打滑加剧,加速度对非承载区滚子影响较大,大载荷以及较小的轴承游隙可以减弱轴承打滑。轴承在加速过程中,滚子转速随时间呈阶梯状增大,而保持架转速随时间呈线性增大。
3) 轴承滚子从承载区进入非承载区时,由加速度的存在以及牵引力的减小,滚子转速略微减小。滚子与内滚道间相对滑动速度ij大于滚子与外滚道间的相对滑动速度oj,相对滑动速度oj方向在最大承载位置发生变化;在非承载区,滚子与内滚道间相对滑动速度较大,增大轴承载荷,减小轴承间隙以及加速度可以减小滚子与滚道间的相对滑动速度。
[1] HARRIS T A. An analytical method to predict skidding in high speed roller bearings[J]. Asle Transactions, 1996, 9(3): 229−241.
[2] CHANG L, CONRY C C T F. Analysis of high-speed cylindrical roller bearings using a full elastohydrodynamic lubrication model, Part 1: Formulation[J]. Tribology Transactions, 1990, 33(2): 274−284.
[3] POPLAWSKI J V. Slip and cage forces in a high-speed roller bearing[J]. Journal of Tribology, 1972, 94(2): 143−150.
[4] 金海善, 朱爱斌, 陈渭. 利用改进牛顿−拉夫逊法的高速圆柱滚子轴承打滑分析[J]. 西安交通大学学报, 2015, 49(1): 133−138. JIN Haishan, ZHU Aibin, CHEN Wei. Skidding analysis of high-speed cylindrical roller bearings using improved Newton− Raphson method[J]. Journal of Xi’an Jiaotong University, 2015, 49(1): 133−138.
[5] 陈渭, 李军宁, 张立波, 等. 考虑涡动工况的高速滚动轴承打滑失效分析[J]. 机械工程学报, 2013, 49(6): 38−43. CHEND Wei, LI Junning, ZHANG Libo, et al. Skidding analysis of high speed rolling bearing considering whirling of bearing[J]. Journal of Mechanical Engineering, 2013, 49(6): 38−43.
[6] TU W, SHAO Y, MECHEFSKE C K. An analytical model to investigate skidding in rolling element bearings during acceleration[J]. Journal of Mechanical Science and Technology, 2012, 26(8): 2451−2458.
[7] CAO Wei, WANG Jiaxu, PU Wei, et al. A study on the effect of acceleration on slip velocity and lubrication performance in cylindrical roller bearings[J]. Proceedings of the Institution of Mechanical Engineers, Part J: Journal of Engineering Tribology, 2016, 230(10): 1231−1243.
[8] DOWSON D, HIGGINSON G R. Theory of roller bearing lubrication and deformation[C]// Proc Lubrication and Wear Convention. London: Instn Mech Engrs, 1963: 216−227.
[9] CAO W, WANG J, PU W, et al. The effect of round corner on lubrication of high speed cylindrical roller bearings considering skidding[J]. Industrial Lubrication & Tribology, 2017(5): 833−843.
[10] LI Junning, CHEN Wenguo. Effects of different structure parameters on skidding of high-speed roller bearing considering bearing whirling[J]. Journal of Vibroengineering, 2014, 16(2): 748−760.
[11] CHEN Jin, LIU Jing, SHAO Yiming, et al. Vibration modeling of lubricated rolling element bearing considering skidding in loaded zone[J]. Journal of Failure Analysis & Prevention, 2014, 14(6): 1−9.
[12] TAKABI J, KHONSARI M M. On the influence of traction coefficient on the cage angular velocity in roller bearings[J]. Tribology Transactions, 2014, 57(5): 793−805.
[13] JOHNSON K L, ROBERTS A D. Observations of viscoelastic behaviour of an elastohydrodynamic lubricant film[J]. Proceedings of the Royal Society of London, Series A: Mathematical and Physical Sciences, 1974, 337(1609): 217−242.
[14] JOHNSON K L, TEVAARWERK J L. Shear behaviour of elastohydrodynamic oil films[J]. Proceedings of the Royal Society A: Mathematical Physical & Engineering Sciences, 1977, 356(1685): 215−236.
[15] BAIR S, WINER W O. A rheological model for elastohydrodynamic contacts based on primary laboratory data[J]. Journal of Tribology, 1979, 101(3): 258−264.
[16] 万长森. 滚动轴承的分析方法[M]. 北京: 机械工业出版社, 1987: 71−78. WAN Changseng. The analysis method of roller bearing[M]. Beijing: China Machine Press, 1987: 71−78.
[17] ZHU D, WANG J, WANG Q J. On the stribeck curves for lubricated counterformal contacts of rough surfaces[J]. Journal of Tribology, 2015, 137(2): 02051-1−10.
[18] ZHU Dong, HU Yuanzhong. A computer program package for the prediction of EHL and mixed lubrication characteristics, friction, subsurface stresses and flash temperatures based on measured 3-D surface roughness[J]. Tribology Transactions, 2001, 44(3): 368−390.
(编辑 赵俊)
Kinetic characteristics of cylindrical roller bearing during acceleration
CAO Wei1, WANG Jiaxu1, 2, PU Wei1, ZHOU Guangwu1, ZHANG Ying3, WU Jiqiang1, REN Si1
(1. School of Aeronautics and Astronautics, Sichuan University, Chengdu 610065, China; 2. State Key Laboratory of Mechanical Transmission, Chongqing University, Chongqing 400044, China; 3. School of Manufacturing Science and Engineering, Sichuan University, Chengdu 610065, China)
In order to analyze the kinetic characteristics of cylindrical roller bearing, a whole roller dynamic model was established considering accelerations, operating conditions, geometry and rheological characteristics of lubricant, and the kinetic characteristics in transient and time-varying condition were investigated. The results show that dynamic model with the consideration of viscoelasticity can improve the accuracy of the model. Accelerations have obvious effect on bearing skidding, especially for rollers in unloaded zone. The accelerations make the skidding of cage and roller serious. When the bearing is during acceleration, the roller speed increases in a stair-step shape with the increase of time, but the cage speed increases in a linear relationship. When roller rotates from the loaded zone to the unloaded zone, the roller speed decreases slightly, and the roller speed increases sharply when the roller rotates from the unloaded zone to the loaded zone. The roller-inner slip velocityijis large than roller-outer race slip velocityoj, and the direction of slip velocityojchanges in the area of maximum roller load position due to the effect of acceleration. The relative slip velocity between the roller and inner race is high in the unloaded zone, and meanwhile, heavy load and small clearance can reduce the slip speed.
bearing skidding, bearing acceleration, cylindrical roller bearing, rheological characteristics
TH132
A
10.11817/j.issn.1672-7207.2018.03.010
1672−7207(2018)03−0583−09
2017−03−14;
2017−05−08
国家自然科学基金资助项目(51435001,51375506) (Projects(51435001, 51375506) supported by the National Natural Science Foundation of China)
周广武,副研究员,从事传动系统动力学研究;E-mail: gwzhou@scu.edu.cn

