变体飞行器有限时间切换H∞跟踪控制
夏川, 董朝阳, 程昊宇, 王青, 王昭磊
(1.北京航空航天大学 航空科学与工程学院, 北京 100191; 2.西北工业大学 航天学院, 陕西 西安 710072;3.北京航空航天大学 自动化科学与电气工程学院, 北京 100191; 4.北京航天自动控制研究所, 北京 100854)
0 引言
相对于传统飞行器,变体飞行器可以通过结构外形的变化来适应多种作战任务、实现最佳飞行性能[1]。由于变体飞行器参数变化剧烈、模型复杂度高、飞行条件多变,在建模和控制领域面临着诸多挑战,一直是各国军事领域研究的热点[2]。
切换线性变参数(LPV)控制理论[3]是解决强非线性、不确定性和参数快时变的一种有效方法。Zhao等[4]针对调参变量测量的不确定性,为切换LPV系统设计了鲁棒控制器,保证了系统达到预设的性能指标。He等[5]和Huang等[6]考虑外部干扰,分别设计了LPV系统控制器并应用于F-16飞机和临近空间高超声速飞行器,保证了系统全局一致渐进稳定。然而,上述文献主要集中研究无限时间上系统的渐近稳定性,没有考虑飞行器在有限时间内的稳定性和收敛性。在许多实际系统中,考虑有限时间内系统状态的有界性和鲁棒性具有重要意义[7],例如变体飞行器的构型转换过程以及高超声速飞行器的机动飞行,都需要保障飞行器在给定时间内的暂态性能。
Wang等[8]和Wang等[9]提出的有限时间稳定性被用于研究有限时间内系统稳定性和控制问题。Xiang等[10]设计了一类有限时间控制器,保证了时滞切换系统有限时间稳定性。Lin等[11]研究了切换系统的有限时间稳定性和有界性问题。Liu等[12]针对异步切换系统使用平均驻留时间(ADT)方法和多Lyapunov函数方法设计了有限时间H∞控制器。
另一方面,系统的能量函数会在切换瞬间跳跃,导致闭环系统性能降低,为了得到切换系统的切换逻辑,Zhang等[13]基于ADT方法研究了一类异步切换线性系统的控制问题,分析了连续和离散系统的稳定性。然而,基于ADT框架的分析方法,在所有子系统下都使用相同的参数,控制器切换逻辑独立于每个子系统的模态,这无疑会引入设计的保守性。江未来等[14]采用ADT方法,以变体飞行器后掠角为调参变量,将后掠角变化引起的系统特性变化抽象为LPV系统,设计了平滑切换鲁棒控制器。但未考虑变形过程中的系统有限时间动态性能,设计结果相对保守。针对这一问题,Zhao等[15]首次使用模态依赖平均驻留时间(MDADT)方法研究了切换系统的稳定性与镇定控制问题,以线性矩阵不等式(LMI)的形式将ADT方法的结论推广应用到MDADT方法,降低了控制器设计的保守性,获得了更优良的系统性能。Lu等[16]针对LPV系统,基于MDADT方法对H∞控制问题开展了研究。
然而,以上工作均未对存在切换的有限时间H∞控制问题进行研究。在变体飞行器变形过程中,研究系统在有限时间内的动态性能和对干扰的鲁棒性,并设计控制器完成对指令的跟踪,对于降低系统设计的保守性具有重要意义。
本文针对存在切换的变体飞行器变形过程中跟踪控制问题,提出一种切换LPV有限时间H∞控制器的设计方法。建立了变体飞行器切换LPV模型,基于MDADT方法和多Lyapunov函数方法分析飞行器系统的有限时间稳定性和有限时间H∞性能,以保证系统稳定性并具有给定的干扰抑制指标。以LMI形式给出了控制器存在的充分条件和求解方法。通过仿真验证了所提方法能够有效跟踪指令信号并具有良好的动态性能,并能够有效抑制切换、外界干扰和变形过程中的不确定性。
1 变体飞行器建模
图1为美国NextGen航空公司研制的变后掠翼飞行器Teledyne Ryan BQM-34“Fire-bee”,该飞行器的机翼后掠角可以在15°~60°之间连续变化,具有巡航、高速、机动等多种可变构型。图1中,λ为后掠角,它的变化会导致机翼面积、翼展、平均气动弦长等模型参数变化,进而引起气动力和力矩、转动惯量、重心等参数变化,产生惯性力和力矩干扰。
飞行器纵向短周期非线性运动方程[17]如下:
(1)
式中:m为总质量;v为速度;α为攻角;q为俯仰角速率;g为重力加速度;θ为俯仰姿态角;S为翼面积;Q为动压;Cl为升力系数;h为高度;Ma为马赫数;δe为升降舵偏角;mw为机翼质量;xw为机翼质心位置;ma为配重质量;xa为配重质心位置;Iy为绕y轴的俯仰转动惯量;c为气动弦长;Cm为俯仰力矩系数。结构参数值见表1[18].

表1 变体飞行器结构参数Tab.1 Configuration parameters of morphing aircraft
升力系数和俯仰力矩系数定义如下:
Cl=Cl0+Clαα+Clδeδe,
(2)
(3)
式中:Cl0、Cm0分别为零升系数和零升力矩系数;Clα、Cmα为与迎角有关的系数;Clδe、Cmδe为与升降舵偏角有关的系数;Cmq为与俯仰角速率有关的系数。
假设飞行器在h=12 500 m高度以Ma=0.55定直平飞,定义ρ=(λ-λ0)/λ0为飞行器后掠角的变形率,其中λ0=15°对应于后掠角最小的构型。由计算流体力学和MATLAB工具,通过插值可拟合得到升力系数与力矩系数随变形率的变化如下:
(4)
将包含mw、ma的项视作由飞行器机翼后掠角变化所引起的广义附加干扰项,采用雅克比线性化方法,推导得出线性化方程为
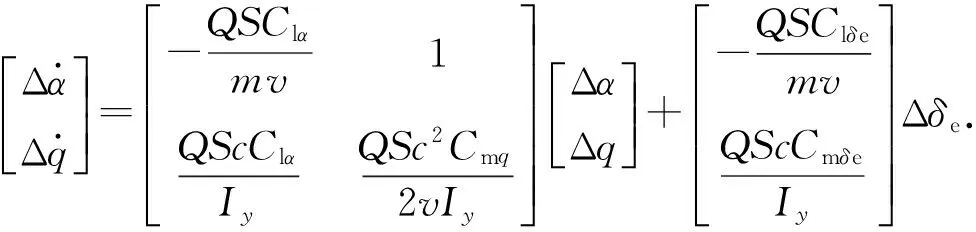
(5)
离散化后可得到变体飞行器的切换LPV模型如下:
(6)
不失一般性,假设(Ai(ρk),Bi(ρk))可控,i∈Θ,Θ={1,2,…,n}为分段连续的切换信号,n为飞行器子系统li的个数,且满足
(7)
(8)

(9)

为了保证输出信号y(k)对指令信号r(k)的跟踪,且在控制器切换和干扰情况下系统仍能保证稳定性和动态性能,定义输出跟踪误差为ε(k)=r(k)-y(k),则飞行器输出信号的跟踪问题可以归结为设计控制器,使得(10)式成立:
(10)
定义误差的积分υ(k)为
(11)
本文设计如(12)式所示的控制器,保证飞行器实现对指令信号的跟踪和对干扰的鲁棒。
u(k)=K1,i(ρk)x(k)+K2,i(ρk)υ(k),
(12)
式中:K1,i(ρk)和K2,i(ρk)为待设计的控制器参数矩阵。
(13)
下面给出如下合理假设:
假设1[12]对于给定的时间常数Tc,时变外界扰动ω(k)满足(14)式:
(14)
2 控制器设计
为设计有限时间H∞控制器,首先给出如下定义。
定义1[19]MDADT. 给定切换信号σ(k)以及0 则称κai为MDADT. 定义2[20]有限时间稳定。对于给定的适维矩阵U>0以及给定的正常数a1、a2、Tc和切换信号σ(k),其中a1 ξT(k0)Uξ(k0)≤a1⟹ξT(k)Uξ(k)≤a2, (15) ξT(k0)Uξ(k0)≤a1⟹ξT(k)Uξ(k)≤a2, (16) 式中扰动满足假设1. (17) 综上所述,闭环系统(13)式有限时间稳定且具有给定的H∞性能γ′>0,当且仅当:1)闭环系统(13)式有限时间有界;2)对于给定的γ′>0,闭环系统(13)式在零初始条件下满足(17)式,其中外界干扰满足(14)式。 由于子系统间的切换,Lyapunov函数会在切换时刻发生跳变,引起动态性能降低。设第i个子系统的激活时刻为ki,系统的Lyapunov函数在切换时刻的跳变率为τi,在子系统内函数值的减少率为si,则可得定理1. Fi(ρk)≤τiFj(ρk), (18) (19) (20) 证明对于(13)式所示的切换LPV系统,选择Lyapunov函数如下: V(k)=ξT(k)Ri(ρk)ξ(k), (21) 式中:Ri(ρk)>0. (22) 用矩阵diag{Fi(ρk),Fj(ρk),I}对(22)式进行全等变换,即可得到(19)式,由上述推导,移项可得 ΔV(k)≤-siV(k)+γ2ωT(k)Gi(ρk)ω(k). (23) 基于以上分析,令π(k)=ωT(k)Gi(ρk)ω(k),对(23)式反复迭代,可得 由η1和η2的定义,可得(24)式和(25)式: (24) (25) 结合ξT(k0)Uξ(k0)≤a1,可得 若闭环系统有限时间有界,则有ξT(k)Uξ(k)≤a2,即 综上所述,如果满足(18)式和(19)式,则闭环系统在MDADT满足(20)式的切换信号作用下有限时间有界。证毕。 定理1采用MDADT方法不仅给出了切换闭环系统有限时间有界的充分条件,保证了系统在有限时间内收敛到给定区间内,使系统响应具有快速性和稳定性,而且充分考虑了每个子系统内切换时刻跳变率、区间内能量函数衰减率的不同,有效降低了保守性。 Fi(ρk)≤τiFj(ρk), (26) (27) (28) 证明选取Lyapunov函数如(21)式所示,在零初始条件下,类似于定理1的推导步骤,可得 (29) 用矩阵diag{Fi(ρk),I,Fj(ρk),I}对(29)式进行全等变换,即可得到(27)式,由上述推导,移项可得 ΔV(k)≤-siVi(k)-yT(k)y(k)+γ2ωT(k)ω(k). (30) 与定理1的证明过程类似,将(23)式中的γ2ωT(k)Gi(ρk)ω(k)替换为ψ(k)=-yT(k)y(k)+γ2ωT(k)ω(k),反复迭代即可得到(31)式: (31) 下面证明鲁棒性。结合零初始条件和Vσ(k)(k)≥0,可以得到: (32) 由(28)式可以得到: (33) 结合(32)式和(33)式,有 (34) 定理2给出了系统满足有限时间H∞性能指标的充分条件,定理3将给出控制器的求解方法。 Fi(ρk)≤τiFj(ρk), (35) (36) (37) (38) 使用本文提出的控制器设计方法对变体飞行器“Firebee”在变形过程中的控制问题进行仿真验证,选取ρk=0,0.1,0.2,…,3共计31个平衡点,对变化的翼面积和气动弦长进行线性插值,结合气动参数对后掠角进行数值拟合,计算得到: 在控制系统设计中,为了保证指令信号的平滑性、避免信号发生突变、保证系统的动态性能,需要对指令信号进行滤波。指令滤波器由幅值限制器和速率限制器组成,其状态空间表达式如(39)式、(40)式所示: (39) (40) 为了对系统的不稳定模态进行补偿,采用如下角速率补偿器解决静不稳定工作点的问题: 式中:K(s)为补偿器的传递函数;Kc和Tf为角速率补偿器的增益和时间常数。 变体飞行器切换控制系统结构图如图2所示。 表2 参数设定和计算结果Tab.2 Coefficients setting and calculated results 设定跟踪指令为攻角指令,在系统能控条件下通过设定指标γ,利用MATLAB的LMI工具箱求解控制器,可得到3个子系统次优H∞控制器的增益矩阵如下: 后掠角变化实现构型转换的变形策略是预先设计好的,变体飞行器后掠角调参变量ρ随时间t的变化关系为 对比划分的3个子系统,得到切换时刻分别为20.26 s,28.77 s,51.23 s,59.74 s. 在存在扰动情况下对系统进行仿真,得到攻角响应曲线、俯仰角响应曲线和升降舵曲线的仿真曲线,分别如图3、图4、图5所示。图3中:Δαcom为攻角指令,ΔαADT为文献[20]设计方法的跟踪曲线,ΔαMDADT为本文所提设计方法计算得到的跟踪曲线。 由图3~图5可知:本文所提MDADT方法在存在干扰时能够较好地跟踪指令,保证系统有限时间稳定和鲁棒,响应比ADT方法快;基于MDADT方法设计的切换控制器比ADT方法更好地抑制了非平滑切换所导致的系统状态激烈响应,跟踪效果比ADT方法好;升降舵响应合理,未发生饱和现象,能够在实际系统上实现。 综上所述,采用本文所提基于MDADT方法的有限时间控制器设计方法,能够保证飞行器系统对姿态指令的精确跟踪,减小切换系统状态响应,保证有限时间内系统对外界干扰的鲁棒性,充分考虑每个子系统的信息和特征,降低设计保守性。 本文针对变体飞行器变形过程中的跟踪控制问题建立了变体飞行器切换LPV模型,在控制器- 子系统切换情况下,基于MDADT方法设计了有限时间H∞控制器,以保证系统在有限时间内的状态响应稳定。通过仿真结果可知:对比ADT方法,本文所提设计方法能够在存在切换和干扰的情况下实现飞行器对指令的准确跟踪;相比ADT方法,本文所设计的控制器充分利用子系统信息,具有更合理的控制器切换逻辑和更小的保守性,控制效果更好。 参考文献(References) [1]Weisshaar T A. Morphing aircraft systems: historical perspectives and future challenges[J]. Journal of Aircraft,2013, 50(2): 337-353. [2]Wang F, Zou Q, Hua C, et al. Disturbance observer-based dynamic surface control design for a hypersonic vehicle with input constraints and uncertainty[J]. Proceedings of the Institution of Mechanical Engineers Part I: Journal of Systems & Control Engineering, 2016, 230(6): 522-536. [3]Eichler A, Hoffmann C, Werner H. Robust control of decomposable LPV systems[J]. Automatica, 2014, 50(12): 3239-3245. [4]Zhao P, Nagamune R. Switching LPV controller design under uncertain scheduling parameters [J]. Automatica, 2017, 76:243-250. [5]He X, Zhao J. Multiple Lyapunov functions with blending for induced L2-norm control of switched LPV systems and its application to an F-16 aircraft model[J]. Asian Journal of Control, 2014, 16(1): 149-161. [6]Huang Y Q, Sun C Y, Qian C S, et al. Non-fragile switching tracking control for a flexible air-breathing hypersonic vehicle based on polytopic LPV model[J]. Chinese Journal of Aeronautics, 2013, 26(4): 948-959. [7]Ali M S, Saravanan S, Cao J. Finite-time boundedness, L2-gain analysis and control of Markovian jump switched neural networks with additive time-varying delays[J]. Nonlinear Analysis Hybrid Systems, 2017, 23:27-43. [8]Wang R H, Xing J C, Wang P, et al. Finite-time stabilization for discrete-time switched stochastic linear systems under asynchronous switching[J]. Transactions of the Institute of Measurement and Control, 2014, 36(5): 588-599. [9]Wang T, Dong C Y, Wang Q. Finite-time boundedness control of morphing aircraft based on switched systems approach[J]. Optik-International Journal for Light and Electron Optics, 2015, 126(23): 4436-4445. [10]Xiang M, Xiang Z. Finite-timeL1control for positive switched linear systems with time-varying delay[J]. Communications in Nonlinear Science & Numerical Simulation, 2013, 18(11):3158-3166. [11]Lin X Z, Du H B, Li S H. Finite-time boundedness andL2-gain analysis for switched delay systems with norm-bounded disturbance[J]. Applied Mathematics and Computation,2011, 217(12): 5982-5993. [12]Liu H, Shen Y, Zhao X D. Asynchronous finite-timeH∞control for switched linear systems via mode-dependent dynamic state-feedback[J]. Nonlinear Analysis: Hybrid Systems,2013, 8: 109-120. [13]Zhang L X, Gao H J. Asynchronously switched control of switched linear systems with average dwell time[J]. Automatica, 2010, 46(5):953-958. [14]江未来, 董朝阳, 王通,等. 变体飞行器平滑切换LPV鲁棒控制[J]. 控制与决策, 2016, 31(1):66-72. JIANG Wei-lai, DONG Chao-yang, WANG Tong, et al. Smooth switching LPV robust control for morphing aircraft[J]. Control and Decision, 2016, 31(1):66-72.(in Chinese) [15]Zhao X D, Zhang L X, Shi P, et al. Stability and stabilization of switched linear systems with mode-dependent average dwell time[J]. IEEE Transactions on Automatic Control,2012, 57(7): 1809-1815. [16]Lu Q G, Zhang L X, Karimi H R, et al.H∞control for asynchronously switched linear parameter-varying systems with mode-dependent average dwell time[J]. IET Control Theory and Application,2013, 7(5): 673-683. [17]程昊宇, 董朝阳, 江未来, 等. 变体飞行器故障检测与容错控制一体化设计[J]. 兵工学报, 2017, 38(4): 711-721. CHENG Hao-yu, DONG Chao-yang, JIANG Wei-lai,et al. Integrated fault detection and fault tolerant control for morphing aircraft[J]. Acta Armamentarii, 2017, 38(4): 711-721.(in Chinese) [18]Seigler T M. Dynamics and control of morphing aircraft[D]. Virginia,VI,US: Virginia Polytechnic Institude and State University, 2005. [19]Zhao X D, Zhang L X, Shi P, et al. Stability and stabilization of switched linear systems with mode-dependent average dwell time[J]. IEEE Transactions on Automatic Control ,2012,57(7): 1809-1815. [20]Amato F, Ariola M, Cosentino C. Finite-time stabilization via dynamic output feedback[J]. Automatica,2006, 42(2): 337-342. [21]Seigler T M, Neal D A. Analysis of transition stability for morphing aircraft[J]. Journal of Guidance, Control, and Dynamics,2009, 32(6): 1947-1954.
∀k∈{1,…,Tc}.
∀k∈{1,…,Tc},




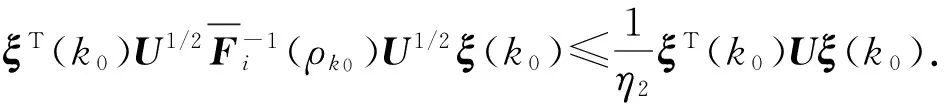
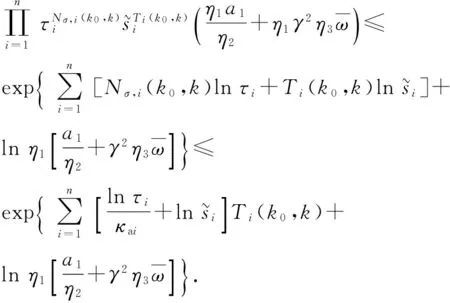

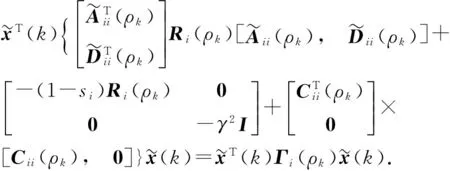


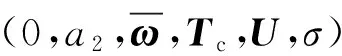

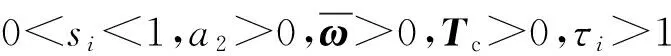

3 仿真分析


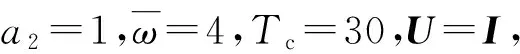


4 结论
——以大别山区9县(市)为例

