预瞄跟随驾驶员模型的复合校正∗

管 欣，陈永尚，贾 鑫，詹 军

前言

20世纪60年代至今，人们对驾驶员方向控制模型的研究根据有无预瞄环节，分为补偿校正模型和预瞄跟随模型[1-2]。预瞄跟随模型考虑了驾驶员的前视作用，在人-车闭环系统评价和智能辅助驾驶领域应用广泛[3-5]。文献[6]和文献[7]中将其用于汽车前车灯自适应控制。文献[8]和文献[9]中将预瞄跟随驾驶员模型用于汽车自适应巡航系统。关于预瞄跟随驾驶员模型，文献[10]～文献[12]中研究了模型参数求解与确定方法，文献[13]中对预瞄跟随驾驶员模型针对急转弯工况进行改进。预瞄跟随驾驶员模型的动态校正环节直接影响控制的位置精度。

传统的动态校正环节采用PD形式的开环校正控制方式进行建模控制[14]，其本质是假定熟练驾驶员能够精确掌握被控车辆的低阶等效逆系统模型，通过精确标定逆模型可以很好地控制人-车闭环系统的性能。但由于汽车动力学除线性区外还有中心区和大滑移区，呈现强烈的非线性特性，要对其逆模型进行精确标定，这导致开环校正控制方式不能自动适应被控车辆的动力学特性变化，给模型应用带来了不便。因此，校正环节采用开环校正控制方式建模，导致模型在应用中面临着汽车非线性动力学的逆模型难以精确标定的问题。

在模型发展过程中，文献[15]中尝试采用PID闭环校正控制方式进行建模，以解决原有模型的标定难题。虽然PID控制无须准确知道被控对象的数学模型，但在驾驶员模型中具有一个纯延迟环节来描述驾驶员的神经滞后特性，而PID控制是根据当前时刻的偏差信号进行校正的，因此，不能有效地消除纯延迟环节带来的影响，控制效果并不理想。通常表现为汽车的实际加速度响应滞后于最优预瞄加速度，或者实际加速度响应在最优预瞄加速度附近持续振荡。另外，同样是由于汽车动力学系统具有强烈的非线性特性，PID参数仍需遍历大量的工作点进行整定，并没有从根本上解决原有模型的标定难题。文献[16]中提出一种采用两个速度下转向盘阶跃试验推测校正环节参数的方法，该方法一定程度上能够适应汽车动力学系统的非线性，但该方法精度受两个标定车速的影响比较大，同时仍须进行相应的标定试验。

针对上述问题，本文中提出一种对汽车非线性动力学具有自适应性的复合动态校正模型。该复合校正模型参数只须通过车辆设计参数估算，无须进行标定。模型采用经典的PD开环模型作为主校正模型，采用BP神经网络PID进行补偿校正。

1　预瞄跟随驾驶员模型

基于预瞄跟随理论的人-车闭环系统框图如图1所示[14]。图中:f为预期路径；fe为预瞄后侧向位置；ε为侧向位置误差；y为侧向位移响应；δsw为转向盘转角；·y·为侧向加速度。

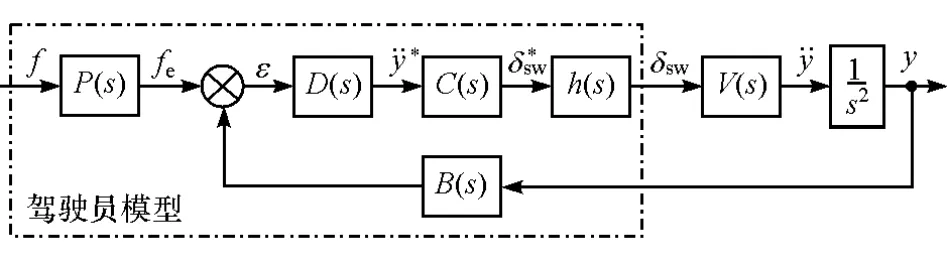
图1　基于预瞄跟随理论的人-车闭环系统框图

人-车闭环系统的传递函数为

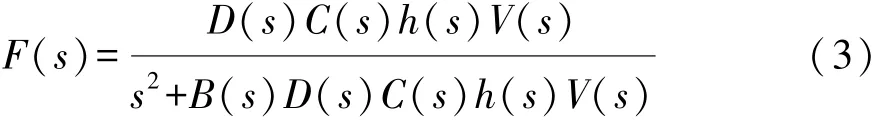
式中:s为拉普拉斯算子；TP为预瞄时间；P(s)为预瞄模块；F(s)为跟随模块，包括预估环节B(s)、决策环节D(s)、校正环节C(s)、滞后环节h(s)和被控车辆V(s)。

对于校正环节C(s)，文献[6]中给出传统的开环校正模型如下:

其中:

式中:Gay，T1和Ty1为与汽车动态响应特性相关的参数；td和th分别为驾驶员神经反应延迟和动作惯性滞后时间，一般取0.2和0.1s。

汽车的侧向加速度对转向盘转角的传递函数可描述为

式中:Gay为汽车侧向加速度稳态增益；T1，T2，Ty1和Ty2等为常数。

2　驾驶员复合校正模型

根据复合校正控制原理[17]，将驾驶员动态校正环节划分成两个部分进行建模:一是主校正部分，代表驾驶员对汽车动力学特性的掌握程度，采用经典的开环校正建模；二是补偿校正部分，代表人的补偿修正能力，采用PID闭环校正建模。驾驶员复合校正模型如图2所示。

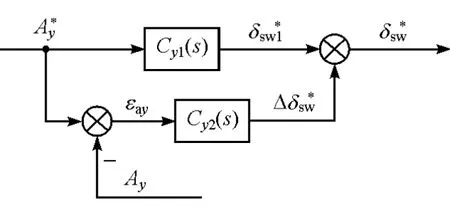
图2　复合校正模型控制框图

图中:Ay∗和Ay分别为最优预瞄侧向加速度和实际的汽车侧向加速度响应；Cy1(s)为侧向主校正部分，其输出量δsw1∗为转向盘主操作指令；Cy2(s)为侧向补偿校正部分，其输出量Δδsw∗为转向盘补偿操作指令；δsw∗为最终的转向盘操作指令。另外，注意到如下事实:习惯驾驶一种车型的人，偶尔驾驶其他车型的汽车，通常会感到不习惯，但一般仍可胜任驾驶任务。根据复合校正模型，相当于驾驶员的主校正参数是按照自己熟悉的车型“标定”出来的，而对于其他不熟悉的车型，主校正参数就会出现偏差，所以人会感到不习惯；然而人自身的补偿修正能力，使之可以适应不同车型的差异。由此可见，复合校正模型能够更为真实地描述驾驶员的控制行为。

3　复合校正模型主校正部分

由于驾驶员复合校正模型允许主校正参数具有一定范围的标定误差，所以只须掌握汽车动力学的主特性便可满足要求。

主校正参数根据汽车动力学的逆模型和驾驶员自身的延迟滞后时间进行确定。当汽车动力学的逆模型标定精度较高时，仅由主校正部分便可保证实际加速度响应与最优预瞄加速度的一致性，补偿校正部分几乎不起作用；当汽车动力学的逆模型标定误差较大时，仅由主校正部分作用产生的加速度响应与最优预瞄加速度之间将会出现较大偏差，补偿校正部分根据加速度偏差信号对主操作指令进行补偿修正，进而促使实际加速度响应与最优预瞄加速度趋于一致。由于补偿校正部分具有自动修正能力，驾驶员复合校正模型允许主校正参数具有一定范围的标定误差。主校正部分采用经典的开环校正建模，其传递函数如下:

其中:

由式(9)可知，汽车主校正环节受汽车的侧向加速度稳态增益Gay和侧向加速度对转向盘转角响应的1阶时间常数T1和Ty1的影响。对于2自由度汽车模型，Gay，T1和Ty1等，都可由汽车前后轮的侧偏刚度、汽车质量、质心到前后轮的距离与绕z轴转动惯量等来直接确定[18]。

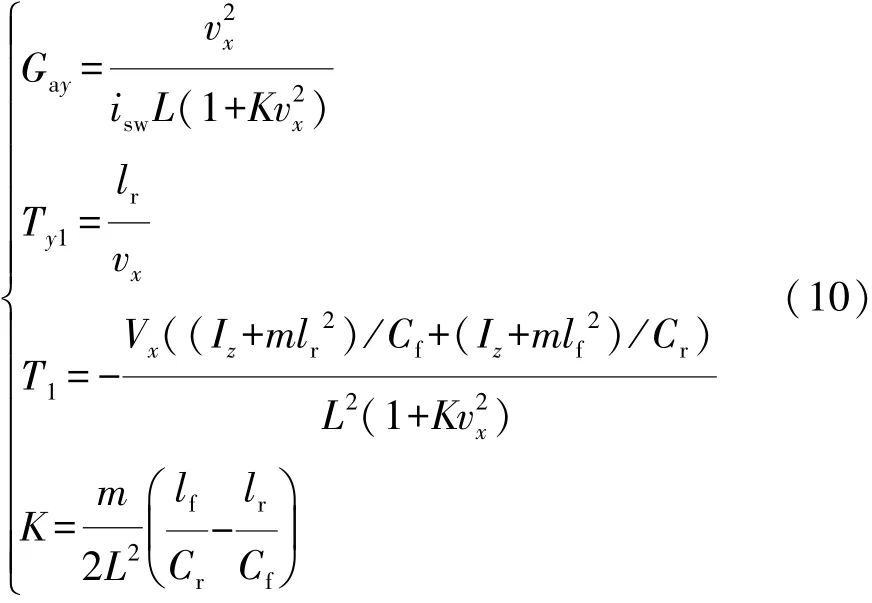
式中:vx为当前车速；isw为转向系角传动比；L为整车轴距；K为稳定性因数；lf和lr分别为质心到前轴和后轴的距离；Cf和Cr分别为前轴和后轴的侧偏刚度；m为整车质量；Iz为汽车绕z轴的转动惯量。

但当被控对象为多自由度汽车模型或者真实车辆时，Gay，T1和Ty1很难直接求出，通常的方法是将被控对象等效为一个2自由度车辆模型，计算出等效2自由度车辆模型的相关参数代入式(10)和式(8)，可求出C0和TC的值。对于2自由度车辆模型的参数无须进行精确的辨识与标定，仅须通过汽车的设计参数求出相应的参数。假设汽车为中心转向，汽车质心位于汽车中心处，前后轴的侧偏刚度取汽车前后轮的侧偏刚度，转向系传动比根据经验取均值。由于这些假设带来的误差由补偿校正模块进行补偿。

式中kf和kr分别为前后轮胎的侧偏刚度。

4　复合校正模型补偿校正

复合校正控制系统的补偿校正部分主要用于消除由于主校正部分参数不准确带来的跟随误差，由于神经网络PID对非线性系统具有很强的适应性且无须大量的标定。采用神经网络PID作为复合校正模型中的补偿校正部分，其控制结构如图3所示[19]。采用反向传播神经网络(BP)对PID的参数进行调整。同时由于BP神经网络具有自学习的特性，基于BP神经网络整定PID参数，当不同汽车作为控制对象时无需再进行参数整定。

PID的控制采用增量式算式:

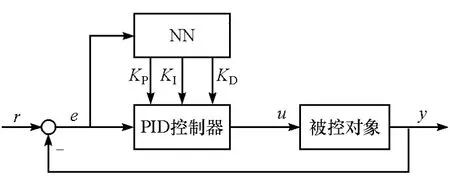
图3　BP神经网络PID控制系统的结构

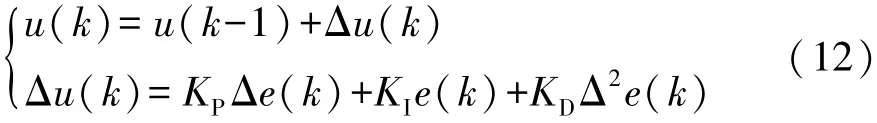
式中:KP，KI和KD分别为比例、积分和微分系数。将KP，KI和KD看为依赖于系统运行状态的可调系数时，可将上式描述为

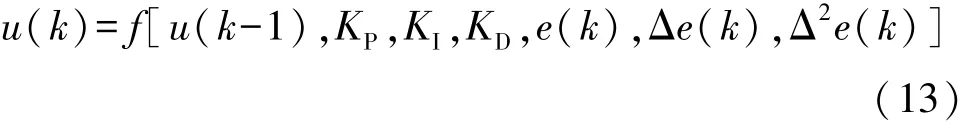
式中 f[·]是与 KP，KI，KD，u(k-1)和 y(k)等有关的非线性函数，可以用BP神经网络NN通过训练和学习来找出一个最佳控制规律。BP神经网络结构如图4所示。

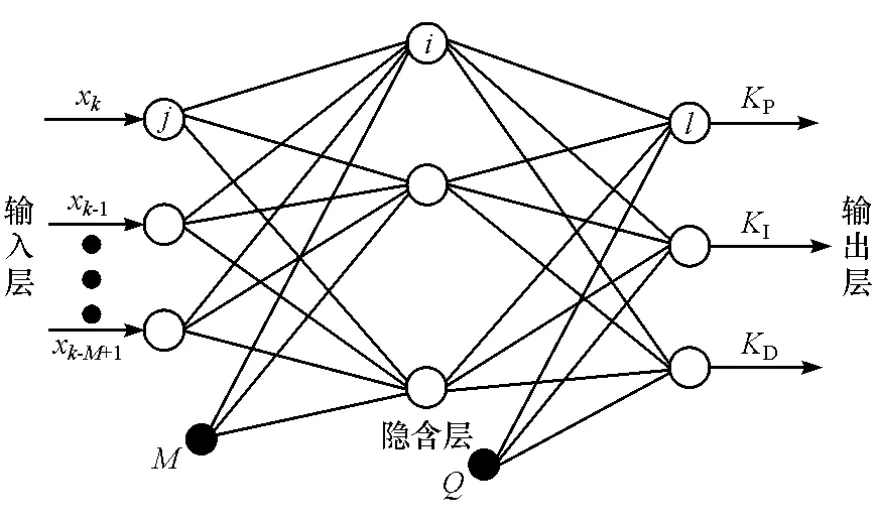
图4　BP神经网络结构

5　试验验证

CarSim是广泛用于车辆动力学仿真的商业软件，本文中选取CarSim中的C级样车，在Matlab/Simulink环境下进行仿真试验分析。

以C级样车为对象，从CarSim中可知车辆的设计参数如表1所示。

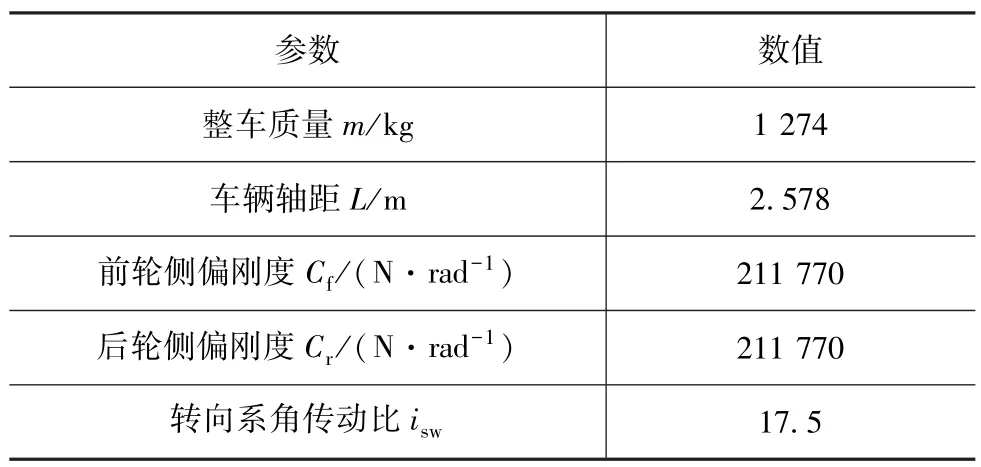
表1　C级样车设计参数

通过式(9)估算等效2自由度车辆模型的参数。之后带入式(8)，可得汽车主校正环节的表达式。采用3层BP神经网络PID控制器作为补偿校正环节控制器，BP神经网络 PID控制器参数如表2所示。

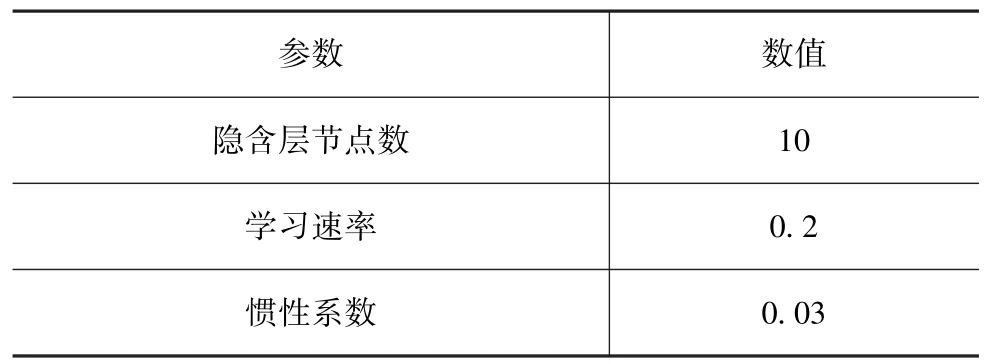
表2　BP神经网络PID控制器参数

5.1　正弦预瞄侧向加速度仿真试验

单独对校正环节进行测试，假设决策环节输入到校正环节的预瞄侧向加速度为正弦输入，为了验证算法在不同车速下的控制效果，控制车速从20加速到120km/h，同时进行幅值为0.5g的正弦预瞄侧向加速度输入，其中g为重力加速度。分别采用复合校正算法和开环校正算法进行侧向加速度控制，其中侧向加速度控制效果和误差如图5所示。转向盘转角及速度变化如图6所示。复合校正模型的神经网络PID参数如图7所示。

图5　正弦预瞄侧向加速度仿真效果

由图5和图6可知，在不同的车速下采用复合校正模型仍然能够精确地控制汽车侧向加速度，而单纯采用开环校正则具有较大的控制误差。其中采用复合校正模型进行控制的最大误差为0.008g，采用开环校正模型进行控制的最大误差为0.24g。由转向盘转角的曲线可以看出，随着车速的提高，转向盘转角降低，在低速的时候为了保证汽车能够到达预期的侧向加速度需要较大的转向盘转角，在高速时则无需这么大的转向盘转角。由图7可知，复合校正神经网络的PID参数随输入和误差的不同而自整定。

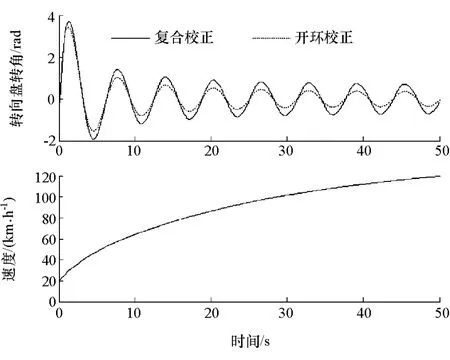
图6　正弦预瞄侧向加速度仿真方向盘转角和速度

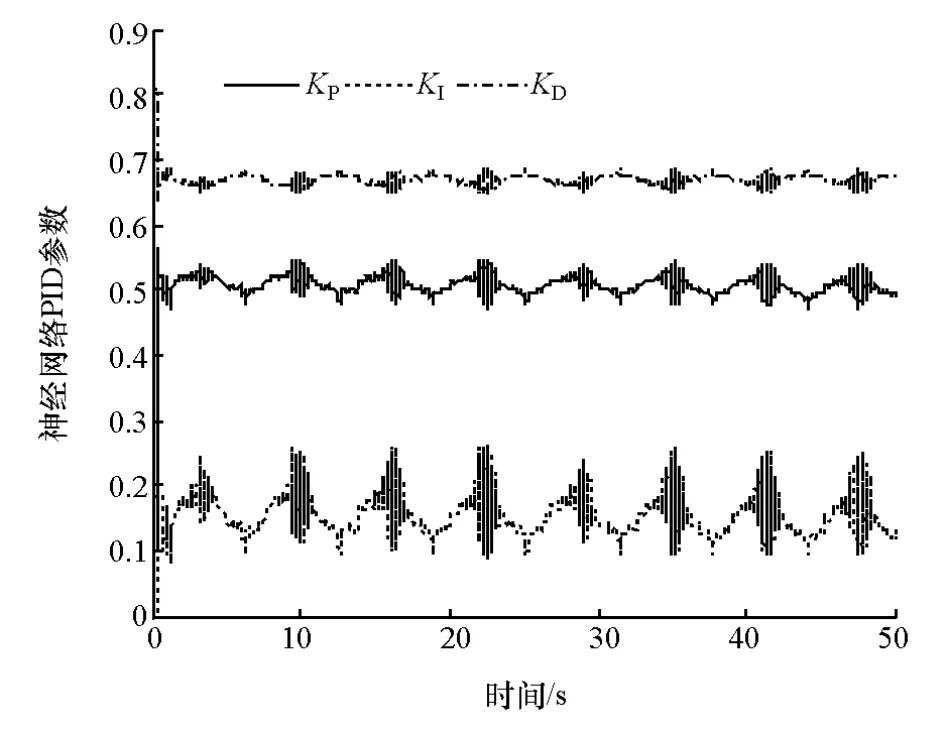
图7　正弦预瞄侧向加速度仿真复合校正神经网络PID参数

5.2　斜坡预瞄侧向加速度仿真实验

对校正环节进行斜坡预瞄侧向加速度输入，侧向加速度输入以0.1的斜率提高到0.5g/s。同样控制车速从20加速到120km/h，分别采用复合校正算法和开环校正算法进行控制。控制效果和误差如图8所示，转向盘转角和速度变化如图9所示，复合校正模型的神经网络PID参数如图10所示。

由图8和图9可知，在不同的车速下采用复合校正模型仍然能够精确地控制汽车侧向加速度，而单纯采用开环校正则具有较大的稳态误差。其中采用复合校正模型进行控制的最大误差为0.001 8g，采用开环校正模型进行控制的最大误差为0.25g。由图10可知，当侧向加速度达到控制的稳态值时复合校正神经网络的PID参数同样达到稳态。

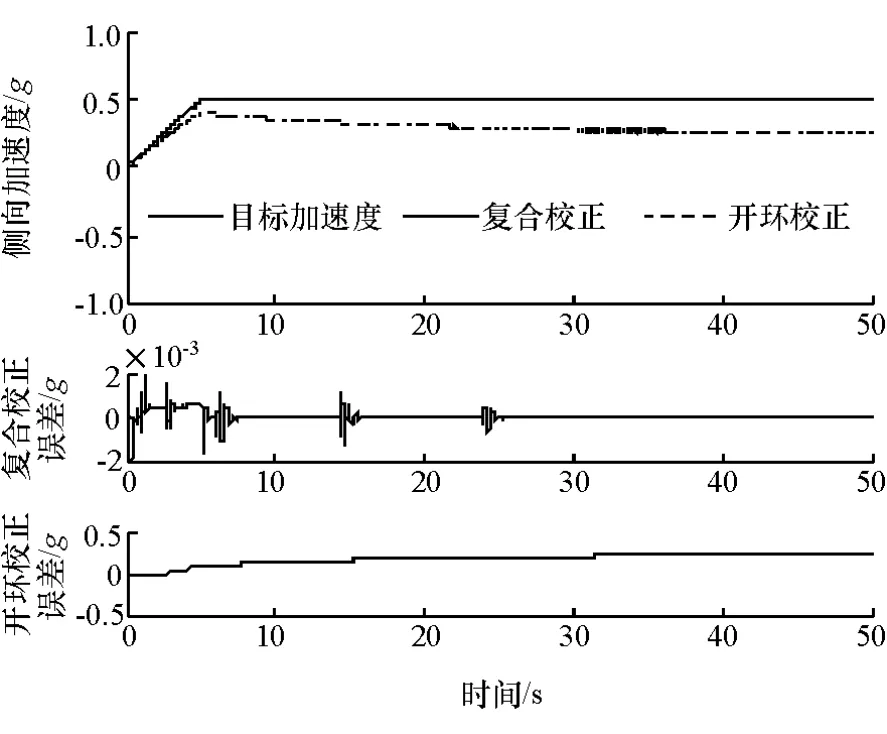
图8　斜坡预瞄侧向加速度仿真效果

图9　斜坡预瞄侧向加速度仿真转向盘转角和速度

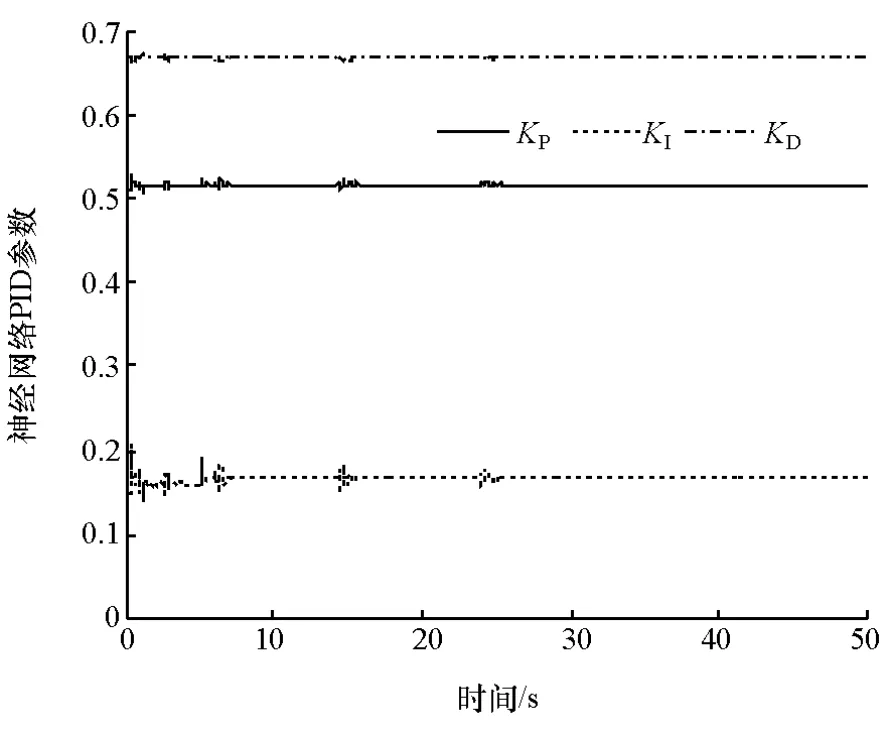
图10　斜坡预瞄侧向加速度仿真复合校正神经网络PID参数

5.3　路径跟随双移线工况仿真

同样以C级样车为对象，采用预瞄跟随驾驶员模型在100km/h车速下进行双移线工况闭环仿真。驾驶员模型参数如表3所示。采用传统的开环校正进行仿真试验，仿真结果如图11所示。最大跟随误差为1.161 4m，最大转向盘转角为19.74°，最大侧向加速度为0.226 9g。

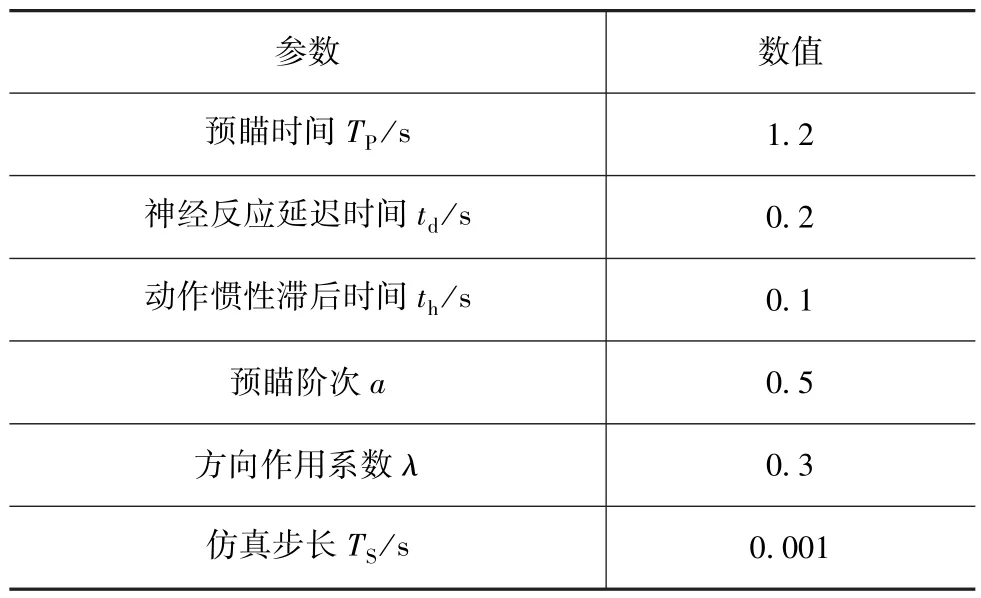
表3　驾驶员模型参数

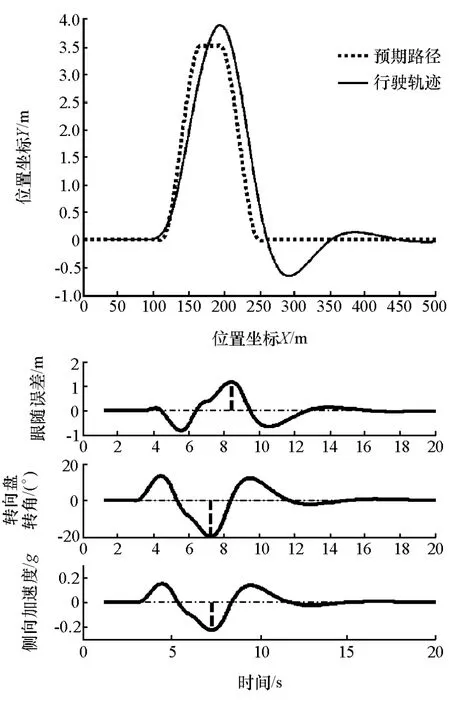
图11　双移线工况仿真曲线(开环校正)

同样以C级样车为对象，采用复合校正模型，进行双移线工况闭环仿真，结果如图12所示。其最大跟随误差为0.356 9m，最大转向盘转角为17.58°，最大侧向加速度为0.202 4g。

由图11和图12可知，采用复合校正的闭环仿真跟随误差较小，其跟随性能有很大的改善。采用复合校正模型的闭环驾驶员模型可以很好地弥补开环校正参数不准确所带来的跟随误差。同时采用复合校正模型的最大转向盘转角和最大侧向加速度均比采用开环控制的转向盘转角和侧向加速度更小，这表明采用复合校正模型的驾驶员模型进行闭环路径跟随时控制更平稳。

5.4　路径跟随蛇行工况仿真

以C级样车为仿真对象在60km/h车速下进行蛇行工况闭环仿真。

采用传统的开环校正模型，进行闭环仿真的结果如图13所示。其最大跟随误差为0.343 8m，最大转向盘转角为 20.88°，最大侧向加速度为0.142 47g。

同样，采用复合校正进行蛇行闭环仿真试验。其结果如图14所示。其最大跟随误差为0.104 9m，最大转向盘转角为 16.4°，最大侧向加速度为0.128 19g。

由图13和图14可知，蛇行工况，采用复合校正的闭环仿真结果比采用开环校正闭环仿真具有更高的控制精度，跟随误差更小。

5.5　驾驶模拟器越过障碍物工况试验

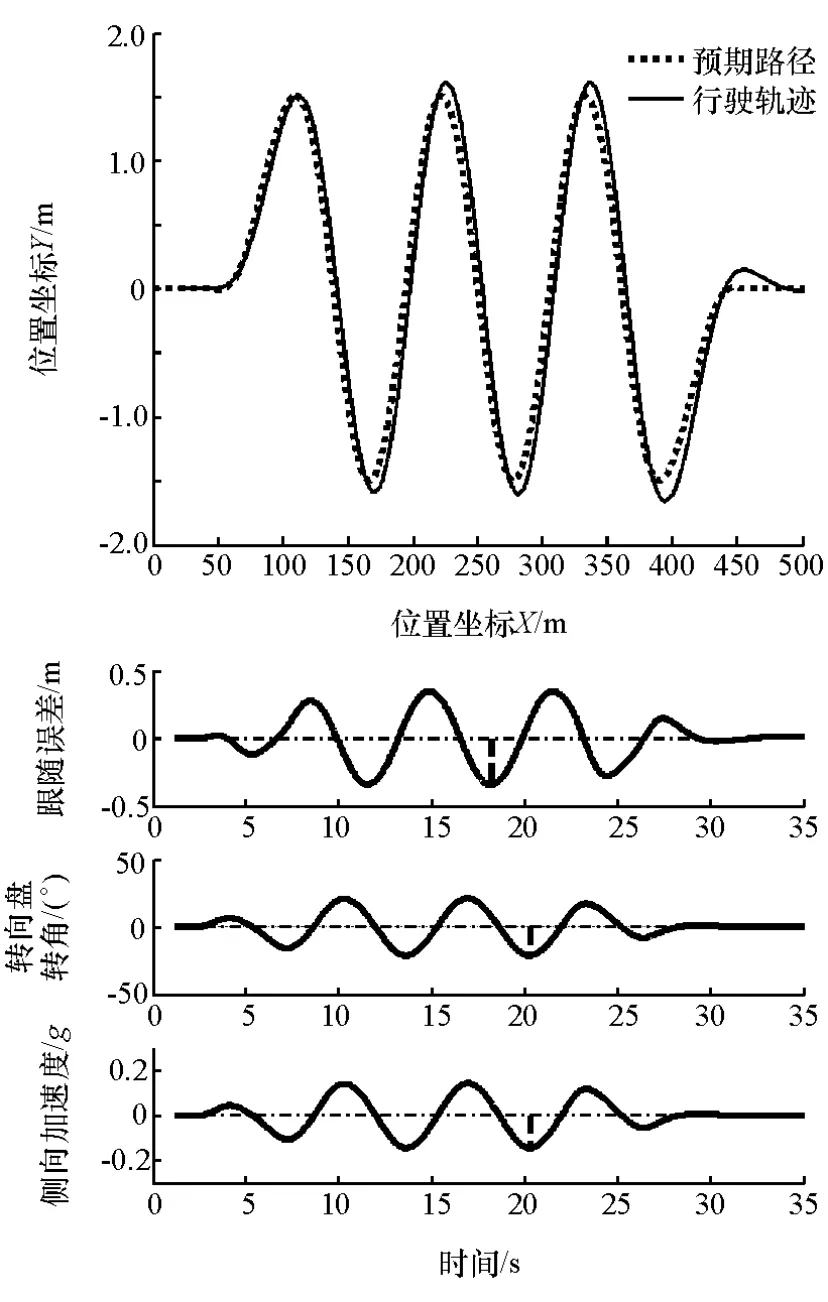
图13　蛇行工况仿真曲线(开环校正)

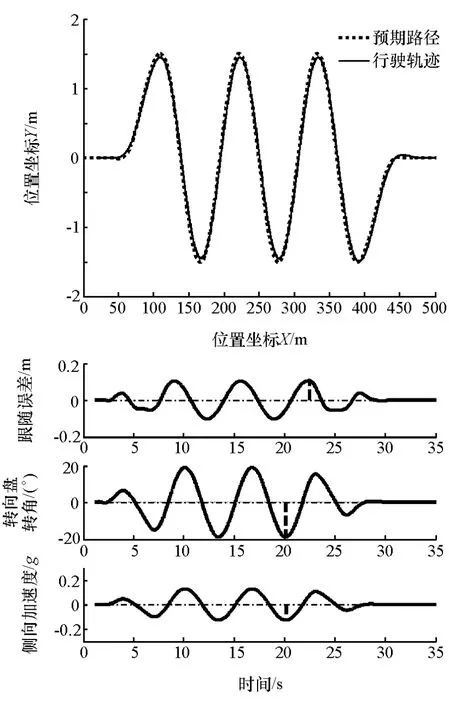
图14　蛇行工况仿真曲线(复合校正)

将本文中提出的复合校正模型与预瞄跟随驾驶员模型嵌入到驾驶模拟器中进行智能车越过障碍物工况验证。驾驶模拟器和验证工况如图15所示。

主车由静止开始加速，目标车速为60km/h，接近前方150m处障碍车。越过障碍车的过程如图17所示。主车在距前方障碍车50m处开始越过障碍车，在越过障碍车50m后回到设定的预期路径。由图可知，采用本文中提出的复合校正模型的预瞄跟随驾驶员模型可以很好地完成越过障碍物任务，同时本文中提出的复合校正模型可精确实现对侧向加速度的控制。

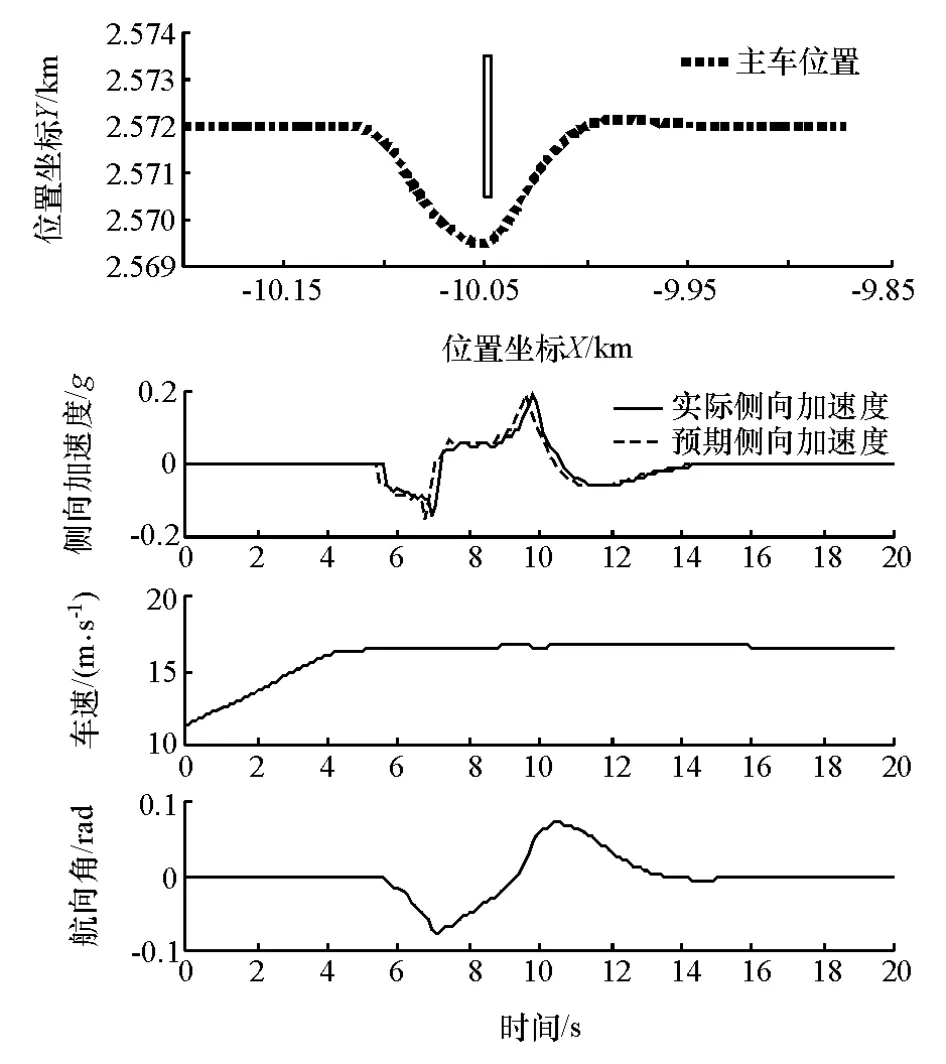
图17　驾驶模拟器越过障碍物工况

6　结论

针对预瞄驾驶员模型中传统的开环校正环节难以适应汽车动力学强非线性的难点，提出一种复合校正方法用于预瞄驾驶员模型校正环节。复合校正模型包含一个传统的微分校正环节和一个基于BP神经网络的PID控制环节，通过试验分析可得到如下结论。

(1)复合校正模型的主校正环节其参数仅须通过汽车的设计参数估算，无须进行复杂的标定。

(2)复合校正模型可很好地适应汽车的非线性动力学特性。当汽车的车速发生变化时，仍能保证对侧向加速度的精确控制。

(3)采用复合校正模型的预瞄跟随驾驶员模型的人车闭环仿真结果表明，采用复合校正的驾驶员模型对路径具有很好的跟随特性，可很大程度上改善跟随误差，可更为准确地用于人-车闭环仿真及智能车辆控制中。

本文中提到的复合校正模型可用于智能汽车侧向加速度控制，结合预瞄跟随驾驶员模型可很好地用于智能汽车的路径跟随控制，提高智能汽车路径跟随的精度，同时减少控制中的标定过程。由于本文中提到的复合校正模型中的主校正部分仍需要前后轴的轮胎侧偏刚度和整车的整备质量等参数，在实际应用中还需要通过设计参数估算或通过试验测量。后续的工作可尝试通过人工智能建立相应的识别模型，仅需要进行简单的场地试验就能通过模型准确的估算出相应参数。

[1] GUZZELLA L，SCIARRETTA A.Vehicle propulsion system[M].Springer Berlin Heidelberg，2007.

[2] GUO Konghui，GUANHsin.Modelling of driver vehicle directional control system[J].Vehicle System Dynamics，1993，22(3):141-184.

[3] CAO J，LUH，GUOK，et al.A driver modeling based on the preview-follower theory and the jerky dynamics[J].Mathematical Problems in Engineering，2013，2013(4):1-10，321-324.

[4] 白艳.汽车易驾驶性评价的随机驾驶员模型[D].长春:吉林大学，2012.

[5] HUANG X C.Driver modeling and simulation based on improved preview follower algorithm[J].Applied Mechanics&Materials，2013，321-324:847-851.

[6] GAO Z，YANG L.Control algorithm of adaptive front-lighting system based on driver preview behavior[C].International Conference on Measurement， Information and Control.IEEE，2014:1389-1392.

[7] GAOZ，LIY.A study of bending mode algorithmof adaptive frontlighting system based on driver preview behavior[C].International Conference on Measurement， Information and Control，2013:1389-1392.

[8] 尤洋.汽车自适应巡航系统自调整因子模糊控制器的优化设计[D].长春:吉林大学，2012.

[9] 高振海，吴涛，尤洋.基于粒子群算法的汽车自适应巡航控制器设计[J].农业机械学报，2013，44(12):11-16.

[10] ZHANG L Z，GUAN H，JIA X，et al.A study on the effect of driver model parameters on the performance of driver-vehicle-road closed-loop system[J].Applied Mechanics&Materials，2014，470:604-608.

[11] 管欣，张立增，贾鑫.误差分析法求解PO预瞄驾驶员模型参数[J].汽车工程，2014，36(2):199-203.

[12] 白艳，贾鑫.最优预瞄加速度驾驶员模型参数试验辨识方法研究[J].汽车工程，2015，37(7):788-793，806.

[13] BAI Y，REN X，FU R.An improvement on optimal preview acceleration driver model on urgent cornering[C].SAE Papers 2015-01-0659.

[14] 郭孔辉.汽车操纵动力学原理[M].南京:江苏科学技术出版社，2011.

[15] 唐林军.驾驶员方向控制模型的控制校正环节的研究[D].长春:吉林大学，2008.

[16] 管欣，陈永尚，贾鑫，等.预瞄跟随驾驶员模型校正环节参数求解方法[J].汽车工程，2016，38(8):941-946.

[17] 胡寿松.自动控制原理[M].3版.北京:国防工业出版社，1994.

[18] MANNING W.Vehicle handling dynamics[M].Butterworth-Heinemann/Elsevier，2009.

[19] 刘金琨.先进PID控制及其MATLAB仿真[M].北京:电子工业出版社，2011.