改进的Dropout正则化卷积神经网络*

满凤环， 陈秀宏， 何佳佳

(江南大学 数字媒体学院， 江苏 无锡 214122)

0 引 言

近年来,卷积神经网络(convolution neural network,CNN)在机器学习和计算机视觉等研究领域得到了很大的关注，但随之出现过度学习(overfitting)的问题，过度学习可表现在随着迭代次数的增加，错误率不再下降。对于过度学习问题，学者们提出了若干正则化方法。Hinton G E等人[1]提出了一个随机的正则化方法—Dropout ，数据在训练时一部分激活单元被抑制，可视为每次是被不同的子模型训练，而在测试阶段则利用预测平均的方法。2014年,Srivastava N等人[2]在全连接层和卷积层使用了Dropout，并得到了很好的效果。Wan L等人[3]提出了一种DropConnect的方法随机抑制权重。Goodfellow I等人[4]提出了一种利用Dropout的Maxout network模型，在一组线性函数中取最大值作为单元的激活值。Zeiler M D和Fergus R[5]提出了随机池正则化方法。

文献[6]提出了在池化层运用最大值Dropout方法。而在测试阶段采用Probabilistic weighted pooling模型平均，实验得到了很好的效果，但该方法仅考虑了Dropout抑制的概率p和被保留的概率1-p的影响，并未考虑池化区域内每个单元值对整个区域的影响。对此,本文提出了一种新的模型平均方法，训练阶段使用最大值Dropout，而在测试阶段结合池化区域内单元值所占的概率和p值求解模型预测的平均值，以同样结构的CNN进行实验并取得了更好的效果。

1 改进的CNN

一个标准的CNN[7]由卷积层和池化层交替出现组成，之后是用于分类的全连接层。CNN有着局部感受域和权值共享等特点，不仅能保持平移不变性、降低特征维数而且还利于泛化。

1.1 卷积层

计算第l+1层第k个输出矩阵的过程可表示为

(1)

al+1,k=f(zl+1,k+bl+1,k)

(2)

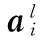
1.2 池化层

(3)

1.2.1 训练阶段的最大值池化Dropout

在池化层使用Dropout，训练阶段时的前向传播用数学公式可表示为

(4)

(5)

池化含有随机性。如图1所示，如果一个池化区域的激活值有1,3,4,7。未Dropout时，输出最大值7，Dropout后，区域内每个单元均可能被抑制，如果3和4被保留，池化后的结果为剩余的最大值4。

图1 最大值池化Dropout示例

1.2.2 测试阶段结合概率的模型平均

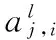
(6)

该文献在测试阶段采用的模型预测平均的方式利用了式(7)得到每个池化区域池化后的值

(7)

式中i=0为池化区域全被Dropout的情况，该方式即Probabilistic weighted pooling。

与文献[6]类似，本文在训练阶段用一个服从多样式分布的二进制掩模修改输入特征图，而在测试阶段考虑到池化区域内每个单元值所占概率的影响。训练阶段，假设第l层的第j个池化区域，使用最大值池化Dropout方法

(8)

但在测试阶段，首先输入特征图每个神经元的值在整个池化区域内所占的概率pi，即

(9)

本文同时考虑到概率pj,i和保留概率p的影响，提出了一种新的模型平均的方法，首先池化区域同乘以p再与其所占概率pj,i相乘，之后池化区域内所有值求和即为池化操作后得到的值

(10)

将这个值作为池化区域内的考虑了所有可能模型的平均的一个近似值。

如果在第l层有r个特征图像，每个特征图像大小为s，池化大小为t，如果是非重叠的池化方法，池化区域可划分为rs/t个，由于Dropout的作用每个池化小块可以有t+1个选择，所以，在l层可能训练的模型数量总数C为

(11)

2 实验结果与分析

本文的CNN结构卷积层和全连接层采用Relu激活函数[10]，Relu造成了网络的稀疏性，并减少了参数的相互依存关系。最后一层的输出连接Softmax分类器。卷积层和全连接层使用的激活函数可简单表示为

al+1=max(0,Wl+1al+bl+1)

(12)

式中al为第l+1层的输入;bl+1为第l+1层相对应的偏置；al+1为计算得到的输出特征图。

Softmax分类器公式表达为

(13)

本文参考文献[6]设置，使用小批量分块的随机梯度下降方法训练模型，每块大小为100，即每次输入100张图像，动量为0.95，学习率为0.1。CNN中所有层的权值初始化以0为均值，标准差为0.1的高斯分布，偏置全部初始化为0，遵守启发式搜索的理论[1]在终止训练前减小2次学习率到当前学习率的1/10。保留概率p=0.5作为默认值。实验环境为:操作系统WIN7，处理器Intel®Xeon®CPU E5—4607 v2@2.60 GHz,2 600 MHz，6个内核,12个逻辑,RAM 32 GB,MATLAB R2012a。模拟实验的原始代码参考来自Vedaldi A等人[11]的深度学习工具箱。

实验中,目标函数是交叉熵代价函数[12]

(14)

式中N为每个min-batch训练样本图像的总数;y为期望的输出;o为神经元的实际输出。

关于权值W对Q求导，利用随机梯度下降算法优化目标函数，第l层的权值更新准则为

ΔWl=δl·ol-1

(15)

式中δl为第l层的误差灵敏度;ol-1为上一层的输出即第l层的输入。误差灵敏度的计算方式分2种情况:当l=L,即最后一层时,利用式(16)计算;当l≤L时,采用式(17)计算

δL=a-y

(16)

δl=δl+1(Wl+1)′·ol·(l-ol)

(17)

式中 ·为2个相同大小的矩阵或者向量对应元素相乘。

采用以下形式表示CNN的结构：28×28-12C5-2P2-24C5-2P2-1000N-10N表示输入图像大小为28×28，第一个卷积层有12个卷积核并且每个卷积核的大小为5×5，第一个池化层的池化区域大小为2×2且步长为2，之后类似，全连接层有1 000个隐含单元，输出层为10个单元(一类对应一个单元)。

2.1 MNIST数据集

MNIST数据集[13]包括60 000张训练图像和10 000张测试图像，每张的大小为28×28，包含0～9中的一个数字。实验中未对其进行任何的预处理，仅将像素值规范到[0,1]范围内。

2.1.1 概率加权的模型平均

为了说明本文方法的有效性，对比本文方法与文献[6]方法，使用2个不同的CNN模型进行训练模拟实验，分别为28×28-6C5-2P2-12C5-2P2-1000N-10N和28×28-12C5-2P2-24C5-2P2-1000N-10N，2种结构在全连接层默认已使用Dropout，只考虑不同方法在池化层的影响。图2给出了相同结构下使用不同方法迭代300次得到的错误率变化曲线。将全连接层使用Dropout的错误率曲线作为对比的基准线。由图可以看出：随着迭代次数的增加，全连接层使用Dropout的方法虽然很快收敛但之后几乎不再下降，本文方法的错误率大部分低于文献[6]Probabilistic weighted pooling法，较好地克服了过度拟合的问题。

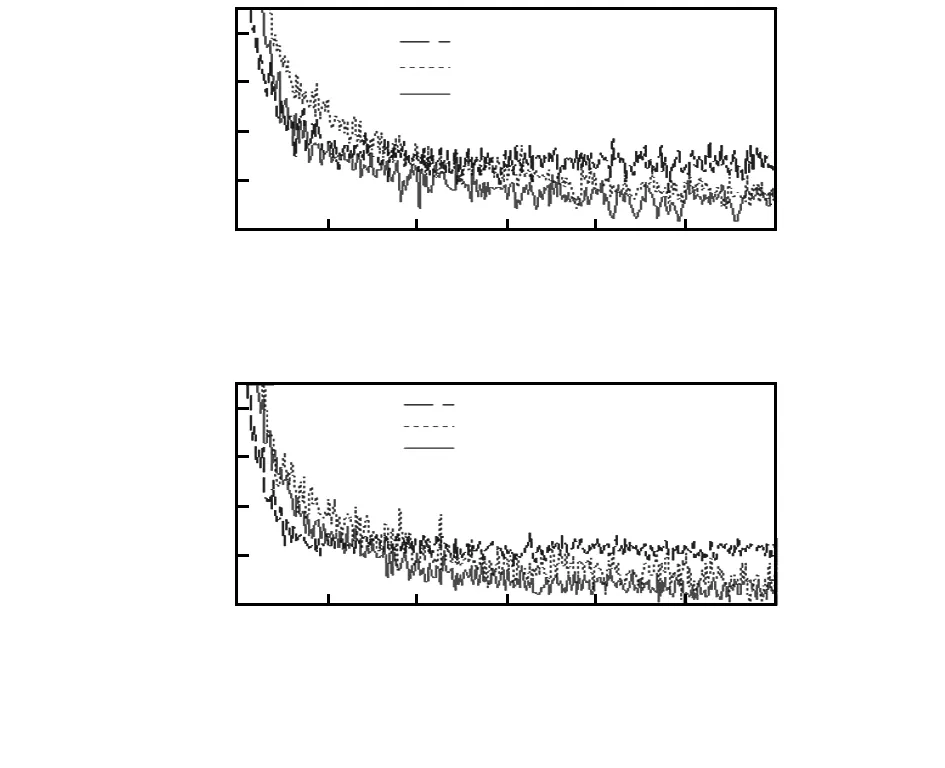
图2 相同结构下不同方法迭代300次的错误率

2.1.2 保留概率p的取值对CNN影响

为了了解p值对本文方法的影响，实验中取不同的p(p=0.3，0.5和0.7)值分别在28×28-20C5-2P2-40C5-2P2-1000N-10N上训练，各自迭代1 000次，得到的错误率e与p之间的关系如图3，相比于其他方法，本文方法即使是不同的p值，也得到了更好的结果。并且可以看到p值取0.5时效果较好。

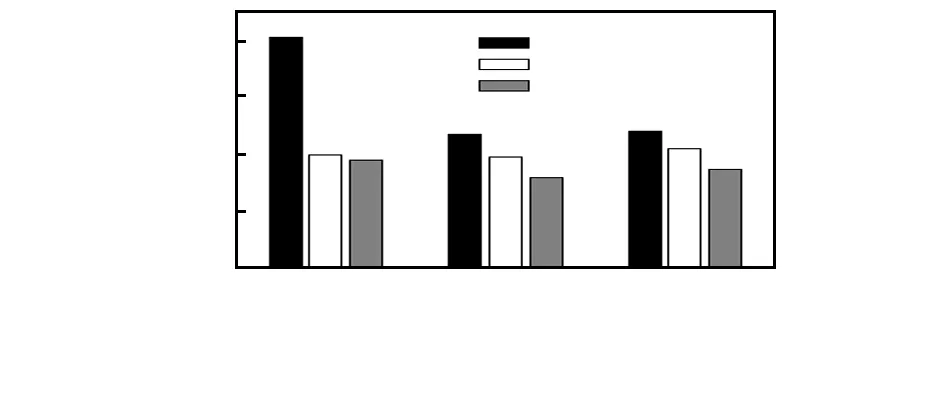
图3 错误率e与p之间的关系

采用与文献[6]同样的CNNs结构28×28-20C5-2P2-40C5-2P2-1000N-10N，表1列出了该方法和其他方法的错误率，对于MNIST数据库，不使用Dropout的最好结果为0.81 %，出现过度拟合现象使得错误率不再下降，在全连接使用错误率约为0.56 %，而本文的方法约为0.32 %，均好于其他方法的结果，证明了可以更好地防止过度拟合的问题。

表1 MNIST上不同方法同一CNN的错误 %

2.2 CMU-PIE数据集

CMU-PIE数据库包含68位志愿者的多姿态、光照和表情的面部图像。本文选取了其中5种姿势分别为上、下、左、右和正面的合集，统一剪切为32×32，在进入CNN之前进行了简单的预处理，灰度化后并将像素值规范到[0,1]范围内。图4所示为图像的部分样例，分别迭代50次的实验结果全连接Dropout、文献[6]、本文方法、文献[5]错误率分别为8.25 %,4.15 %,3.45 %,4.70 %。本文方法错误率约为3.45 %，比文献[6]的方法降低了0.70 %，说明本文方法在其他数据库上也能更好地防止过度学习。

图4 CMU-PIE数据集部分示例

3 结 论

基于Dropout的作用，本文提出了新的模型预测平均值的方法，训练阶段使用最大值池化Dropout法对输入特征图池化，而在测试阶段结合保留概率和单元值概率加权求模型平均，并且得到了更好的识别率，并防止过度拟合的问题。但用时与文献[6]Prob weighted pooling方法相近。未来的研究工作是在本文CNN的基础上改变其激活方法等，使其不仅能防止过度拟合的问题还能更快收敛。

参考文献:

[1] Hinton G E,Srivastava N,Krizhevsky A,et al.Improving neural networks by preventing co-adaptation of feature detectors[J].Computer Science,2012,3(4):212-223.

[2] Srivastava N,Hinton G,Krizhevsky A,et al.Dropout:A simple way to prevent neural networks from overfitting[J].The Journal of Machine Learning Research,2014,15(1):1929-1958.

[3] Wan L,Zeiler M,Zhang S,et al.Regularization of neural networks using dropconnect[C]∥Proceedings of the 30th International Conference on Machine Learning,Atlanta,USA,JMLR Workshop and Conference Proceedings,2013:1058-1066.

[4] Goodfellow I,Warde-farley D,Mirza M,et al.Maxout networks[C]∥ Proceedings of the 30th International Conference on Machine Learning,Atlanta,USA,JMLR Workshop and Conference Proceedings,2013:1319-1327.

[5] Zeiler M D,Fergus R.Stochastic pooling for regularization of deep convolutional neural networks[J/OL].arXiv preprint,(2013—01—16)[2016—06—17].https:∥arxiv.org/abs/1301.3557.

[6] Wu H,Gu X.Towards dropout training for convolutional neural networks[J].Neural Networks:The Official Journal of the International Neural Network Society,2015,71:1-10.

[7] Bouvrie J.Notes on convolutional neural networks[R].Cambridge:MIT CBCL,2006:38-44.

[8] 洪 磊，龚雪飞，孙寿通，等.Adaboost集成BP神经网络在传感器阵列检测系统中的应用[J].传感器与微系统，2015,34(4)：148-150.

[9] 康国炼，杨遂军，叶树亮.改进BP算法在热流传感器温度补偿中的应用[J].传感器与微系统，2016,35(2)：154-156.

[10] Nair V,Hinton G E.Rectified linear units improve restricted Boltzmann machines[C]∥Proceedings of the 27th International Conference on Machine Learning,Haifa,Israel,JMLR Procee-dings,2010:807-814.

[13] Niu X X,Suen C Y.A novel hybrid CNN-SVM classifier for recognizing handwritten digits[J].Pattern Recognition,2012,45(4):1318-1325.

[11] Vedaldi A,Lenc K.Matconvnet:Convolutional neural networks for MATLAB[C]∥Proceedings of the 23rd ACM International Confe-rence on Multimedia,ACM,2015:689-692.

[12] Abdel-Hamid O,Mohamed A,Jiang H,et al.Convolutional neural networks for speech recognition[J].IEEE/ACM Transactions on Audio,Speech,and Language Processing,2014,22(10):1533-1545.