在探究中感悟、明晰和深化——《因数与倍数》课堂实录与反思

刘红专

【教学实录】

一、交流和梳理预习获得，提高对因数与倍数的认识

师：关于因数与倍数，你已经知道了什么？（学生说）让我们一起来梳理、体会刚才同学们说的这些，看看我们还能有哪些收获？

1．摆长方形。

师：一起看大屏幕，这里是12个同样大的正方形，用它们拼成一个长方形，可以怎么拼？（稍后）用一道乘法算式表示你的拼法？（学生说算式，教师板书算式，写出算式后屏幕出示拼法）

2．因数和倍数概念。

（1）例题。

师：我们看这表示不同拼法的三个乘法算式，第一个，4×3=12，在数学上我们也说，4和3都是12的因数；反过来 12是4的倍数，12也是3的倍数。

（2）另两道算式。

师：6×2＝12 这个乘法算式，谁是谁的因数，谁是谁的倍数？

（学生说）

师：12×1＝12，这个算式呢？请你来说（指名）。

（3）自己写乘法算式说说。

师：能再写两个这样的乘法算式来说说吗？

（学生说算式教师板书）

师：如学生刚才说出 2×4＝8，教师写一个8×3＝24）我写一个，谁来说？（学生说后，教师质疑）同样是8，怎么一会儿是倍数，一会儿又是因数了呢？（学生说）所以说因数和倍数时一定要说谁是谁的因数，谁是谁的倍数。

（4）建模。

师：我们看看这些算式，想想我们刚才说的，你想到了什么？

生：只要是乘法算式就可以说出谁是谁的因数，谁是谁的倍数；乘法算式中两个乘数是积的因数，积是两个乘数的倍数。

师：你真厉害！谁能用一个式子来代表所有的乘法算式，并说出两个乘数与积的关系？

生：a×b=n，a和 b 是 n 的因数，n是a和b的倍数。

师：a×b=c 可以吗？（改板书：a×b=c）a和 b 是 c的因数，c就是a和b的倍数。同学们，因数与倍数的关系与生活中师傅与徒弟的关系是一样的，都是相互依存的。（板书：相互依存）

师：如果是一个除法算式(出示24÷3=8)，能说出谁是谁的因数，谁是谁的倍数吗?（学生说）告诉大家你是怎么想的？

（6）再看：（课件出示）321

师：没有算式了，还能说出它们之间因数和倍数的关系吗？跟我们说说你是怎么想的？

师：2个数可以，5个数呢？（课件出示：3、4、18、20、36） 选两个数，说一说谁是谁的因数？谁是谁的倍数？

（学生说）

师：看来同学们对于因数和倍数已经基本掌握了，不过刚才老师在听的时候发现一个奥秘，你们有没有发现？（好几个数都是36的因数）谁能把5个数中哪些数是36的因数一口气说完？

生：3、4、18、36。

师：36的因数只有这4个吗？

生：不是，还有 1、9、6。

师：看来要找出36的一个或几个因数并不难，难的是你有没有能力把36的所有因数都找出来？你可以吗？ 好，拿出作业纸，开始。

二、探索找倍数和因数的方法

1.找一个数的因数。

（1）交流。

反馈分层：把学生的作业分类并编号：不全的①，全且有序②。（一对一对写，从小到大写）

不全的：

师：详细读一读学生的解答，然后你们给他一个评价。

（学生说）

师：这个同学找出的因数有没有值得肯定的地方？（都是对的）只是没有找全。少了哪些数？你觉得这个同学没有找全的原因是什么？

学生分析原因：一个乘法算式或一个除法算式来做的话，是一个个找，还是两个两个找到？按一定的顺序找和写。

全且有序的：

第一种：一对一写的。

师：你看出什么来了？

生：是一对一对找的。

第二种：从小到大写的。

师：这个同学中间怎么空了这么大一段呢？谁知道？（几个学生说了都没有说对），这位同学你说说这中间怎么空这么一段？

生：一对一对找，找到后写的时候从小到大一前一后写成从小到大的样子，找到最后中间就空了一段了。

师:这个同学这样的方法好不好？好在哪儿？

生：既有序一对一对找了，又能从小到大排了。36的因数也可以用集合图来表示。

师：用这个方法我们再来有序找找15和16的因数有哪些？

（找后反馈）

师：观察这3个数的所有因数，有什么发现？

屏幕出示：一个数最小的因数是1，最大的因数是它本身。

（2）因数特点的应用。

课件出示：①24最小的因数是几？最大的因数呢？②一个数最大的因数是30，这个数是多少？

2.找一个数的倍数。

小结过渡：我们会有序地找一个数的因数了，那怎么有序地找一个数的倍数呢？比如3的倍数（课件出示）有哪些？会找吗？

师：好，写在作业纸上。

学生找了一会儿后教师问：3的倍数你找得完吗？为什么？怎么办？

师：请你来说找到了3的哪些倍数？

师：一般是从小到大依次写5个后添加省略号。

师：你是怎样找的？

出示：一个数的倍数也可以用这样的集合图来表示。

师：用这样的方法再来找一找2的倍数和5的倍数吧。

找一个数倍数的特点：

师：我们来看看这3个数的倍数（手势），你能发现什么？

屏幕出示：一个数最小的倍数是它本身，没有最大的倍数。一个数倍数的个数是无限的。

补充完整：一个数因数的个数是有限的。

考考你：（出示8）一个数最小的倍数是8，那这个数是几？它最大的因数是几？

三、巩固练习

1.请你判断。

1.2×5＝6，1.2和 5是 6 的因数。（）

12+7＝19，12是19的因数，19是7的倍数。（）

当a和b是c的因数时，c就是a和b的倍数。（）

2.游戏。

下面老师和你们来做一个无声的数学游戏，请看规则！

规则：根据出现的题目要求静静思考，想好后拿出课桌里的卡片，听老师的指令。

（1）我是20，我找我的因数。

师：拿出课桌里的卡片，卡片上数是20的因数的同学请拿着卡片站到老师旁边来。

（2）我是10，我找我的倍数。

师：手中是10的倍数的同学请拿着卡片站到老师旁边来。

拿着卡片10的同学在别的符合要求的同学都上来以后，匆匆上来，老师让他站在最边上，问他要不要上来，学生说要，一一看过后，发现有一个5，这位同学想下去，老师让他先留下，问同学们5要不要上来，为什么？因为5是10的因数不要上来。同学们掌声请他们上位。

我的最小倍数是8，我是？

我的最大因数是8，我是？

第一次这位拿着8的同学爽快地上来了，且只有这一位同学上来，第二次这位同学犹豫了，想上来又没有上来，老师问这位同学该不该上来？

师：他的这两次连续单独到老师这里来有没有让你们明白到了什么？

生：一个数最小倍数是它最大的因数，都是它本身。

（3）我是1，我找我的倍数。

师：卡片上的数符合要求的同学请坐正。

师：你们为什么都坐着呀？你们手中的数都是1的倍数，反过来1是你们所有数的？（因数）

四、全课总结

师：同学们，今天这节课我们学习了因数与倍数，静静地回想，这节课你学到了什么？（讲后出示）

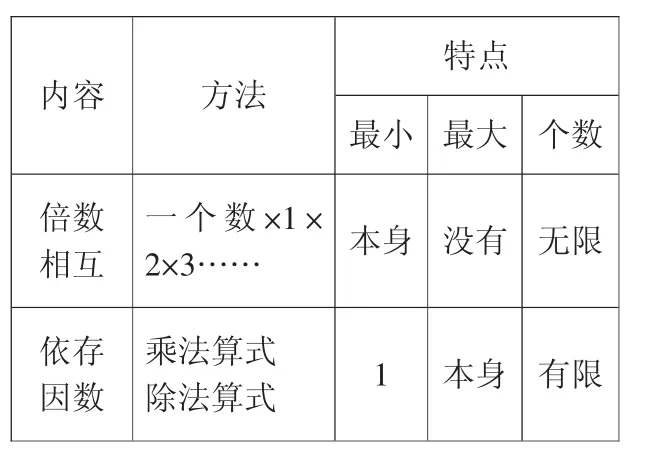
特点最小　最大　个数倍数相互内容　　方法一个数×1×2×3……　　本身　没有　无限依存因数乘法算式除法算式　1　　本身　有限

师：其实关于因数与倍数的知识远远不止这些，随着以后的学习，你们会知道得更多更多！

【课后反思】

本节课，我引导学生在预习之上展开因数与倍数知识的学习；在自主找寻一个数的因数与倍数之中提炼方法；从游戏中感悟、明晰和深化寻找一个数的因数与倍数的关键与一个数的因数、倍数与它本身的关系。这样教学，学生学得愉快、满足和踏实，课堂中生成的两朵浪花更是弥足珍贵：

1. 如改学生 a×b=n 为 a×b＝c更好。

在构建乘法算式中因数与倍数的关系时，学生说可以用a×b=n来表示所有的乘法算式的时候，如能把学生的说法改成a×b＝c该多好，学生极强的概括能力、符号化思想，朦胧的方程意识多么可贵，学生的想法很好地表达了乘法算式中因数与倍数的关系，还很自然地透出方程的思想。

2.迟到的 10，多出的 5，犹豫的8。

这三位同学的行为反映出找寻一个数的因数和倍数时学生会出现的所有常见问题，这个游戏让同学们印象深刻，进而更好地明晰一个数的因数、倍数怎么找，要注意什么？一个数最大的因数和最小的倍数都是它本身，1是所有非0自然数的因数，这些知识的获得更是永远不会忘记。