基于经验 思维可视——《等值分数》的教学思考与实践

葛素儿

【设计意图】

“分数的基本性质”是人教版五年级下册的教学内容。在教材研读中，我们发现大陆的编排和台湾的编排有很大的差异。大陆的教材都出现了“分数的基本性质”这一名称，编排在五年级上册或下册，紧接着是约分、通分、分数大小比较、异分母加减法等知识。而台湾版则是在四年级下册编排了“等值分数”，再在五年级上册编排约分、通分等相关知识。

台湾版的编排有什么好处呢？研究表明，儿童对概念的理解往往是机械性的，即只知道要将分子、分母同时乘以或除以同一个数，却不了解等值分数中隐含着分割、单位量转换以及单位分数等概念。笔者发现，台湾版的教材基于学生的生活经验和已有的知识经验为基础，从具体的量到分率，在运用分一分、涂一涂、画一画、找一找等活动中理解分数的“等价类”思想，相信这样一节以理解等值分数为主线的课，会为学生今后学习分数基本性质、比的基本性质以及七年级的分式基本性质搭建扎实的“脚手架”。基于这样的考虑，笔者想在四年级这个学习阶段，参考台湾教材的编写思路，引导学生经历一节探索等值分数的课，帮助学生去体会等价类思想，促进其对等值分数的意义理解。

【教学过程】

一、等值活动1：发现和n、m是非0自然数）的等值关系

1.观察分数墙：你能在这面墙中找到哪些分数呢？

2.分解分数墙：你们知道这面墙是怎么形成的吗？老师把这面墙拆开（动态依次呈现，说一说这些分数分别表示什么意思？那么又表示什么意思？它们之间有什么关系呢？请同桌互相说一说。

追问：你还能说出与1相等的其他分数吗？为什么这些分数可以用等号连接呢？

3.揭示课题：像这样的分数叫等值分数，刚才找了与1相等的等值分数，那么你会寻找与相等的等值分数吗？这就是本课我们要研究的数学问题。

【设计意图：以分数墙为可视化图示工具，在观察、拆解分数墙的过程中，激活学生已有的知识经验，在寻找与1相等的分数过程中初步感悟等值分数的内涵。】

二、等值活动2：发现与相等的分数

1.出示前测题一：孙悟空说：我把这块西瓜平均分成2份，每人1份吧？猪八戒很不开心地说：才1块，太少了。孙悟空笑嘻嘻地说：那平均分成4块，每人2块，怎么样？猪八戒连声说好，但拿到西瓜后又觉得哪不对。

能用图将题目的意思表示出来吗？猪八戒得到的西瓜多了吗？

2.反馈前测结果：全班36名同学，只有1人认为猪八戒得到的西瓜变了。那么等于吗？

（1）辨析1：认为变了的学生是这样画图的，因此他认为猪八戒多了1块，你怎么看？

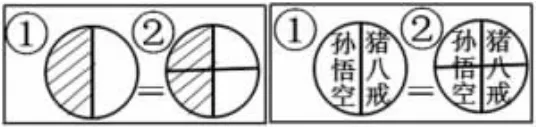
【设计意图：基于前测结果的分析，从“部分—整体”的关系入手，借助图示，透过不同的等分割活动，引导学生在观察、比较、说理的可视化学习中理解的等值关系，并能继续寻找与相等的分数，初步体会“等价类”思想。】

三、等值活动3：发现分别与相等的分数

追问：这些图有什么相同的地方？能让人一眼就看出这两个分数一样大吗？

（2）出示前测题二：图中的阴影部分你能用至少四个分数来表示吗？你能判断它们的大小吗？

（3）呈现前测结果：28人做错。呈现部分学生错例。

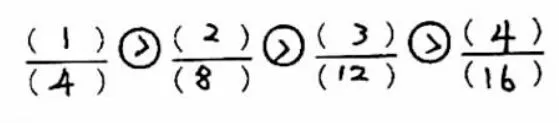
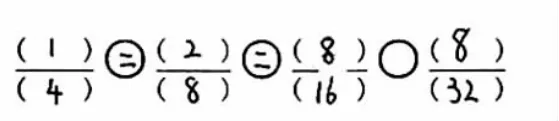
（4）判断错例：错在哪里？你能说说为什么吗？

（1）追问1：什么变了？什么不变？反馈时将格子图转化为线段图，从测量意义上理解这三个分数在同一个点上。

【设计意图：创设自主探究的数学情境，引导学生在画图中自觉运用不同的直观模型解释与相等，从“部分—整体”关系慢慢过渡到“比”的意义和“测量”的意义等不同层级的等值分数的理解，在可视化的图像表征与语言解释中发现真分数的等值关系，进一步体会“等价类”思想。】

四、等值活动4：结合具体情境，寻找与几分之几相等的分数

1.分苹果：（1）分一分、画一画、填一填：1盒苹果有12个，盒是几个？盒是几个？

延伸：蜗牛2小时爬行5米，照这样的速度，6小时爬行几米？如果爬行30米，需要几小时？如果老师把它变变形，你能用今天学习的等值分数来解释吗？

【设计意图：拓展知识的体验背景，引导学生在具体的生活情境中寻找与几分之几相等的等值分数，在理解具体量的等值关系基础上进一步理解等值分数的内涵，同时为后续知识做铺垫。】

五、等值活动5：在分数墙中寻找等值分数

1.思考：这节课我们学习了等值分数，你认为什么样的分数是等值分数？怎么找到一个分数的等值分数呢？引导学生说出：要找一个分数的等值分数，可以把分子、分母同时乘或除以一个相同的数（0除外）。

【设计意图：整节课的学习从分数墙出发，再回到分数墙，借助可视化的图示，引导学生自主梳理知识，尝试概括与归纳等值分数的内涵以及找等值分数的方法，促进知识的自主建构。】

【教学反思】

美国学者莱许等指出：“实物操作只是数学概念发展的一个方面，其他的表述方式，如图像、书面语言、符号语言、现实情境等，同样也发挥了十分重要的作用。”本节课的学习基于学生的经验，通过“直观地看”“出声地想”“形象地画”等可视化的图像表征，引导学生主动理解与感悟分数的等值关系。这样的学习既基于学科本质，又尊重儿童特质，关注思维的生成、方法的领悟、经验的积累，无疑是具有生命力的。