基于概率分析方法的混凝土疲劳寿命模型比较

(郑州工业应用技术学院建筑工程学院　河南　新郑　451150)

引言

自从1829年德国采矿工师W.A.J.Albert提出第一个疲劳问题研究报告以来，人们对疲劳问题的研究已经持续将近两个世纪，但仍有许多问题困扰着人们。1939年之前，对混凝土疲劳寿命的概率分析，基本上都是采用对数分布或对数正态分布。但在1939年，瑞典人Weibull提出了一种描述材料疲劳强度的分布模型，即Weibull分布模型。该模型参数能较好地反映随机荷载下机械产品及其零件的疲劳寿命和疲劳强度。经过多年来国内外广大学者的深入系统地研究，不仅证明了混凝土疲劳寿命既服从对数正态分布又服从两参数Weibull分布，并通过概率函数研究了这两种函数的逼近性，对混凝土的疲劳寿命预测更加合理。

一、结构可靠度理论

假设结构或构件能完成预定功能(Z≥0)的概率称为可靠概率，亦称为可靠度(ps)，而不能完成预定功能的概率(Z<0)，则称之为失效概率(Pf)。又假设功能函数(Z)仅与作用效应(S)和结构抗力(R)两个基本变量有关，则结构功能函数即为:

Z=g(R，S)=R-S

当R、S均服从正态分布，且相互独立时，则结构的失效概率为

当R、S属于其他概率分布，且相互独立时，则结构的失效概率为

(一)对数正态分布统计理论

在疲劳理论中，常用的对数正态分布分布形式为Y=lg(X)，其对数正态分布分为

基本变量X的概率密度函数为

对数正态分布的累积分布函数为

(二)Weibull分布统计理论

在某一特定循环荷载作用下，混凝土疲劳寿命N服从一定的分布规律，用Weibull函数可表示为

由于混凝土材料的离散特性，因此可取Weibull频率函数中的最少寿命参数N0为0，则三参数Weibull函数可简化为两参数的Weibull频率函数

若试验数据线性回归表明Y与X之间线性关系良好，则说明数据符合两参数威布尔分布。

二、混凝土疲劳寿命的概率分析

以试验数据如表1所示为例，利用上文推导结果对混凝土疲劳寿命进行概率分析结果分别如表2所示。

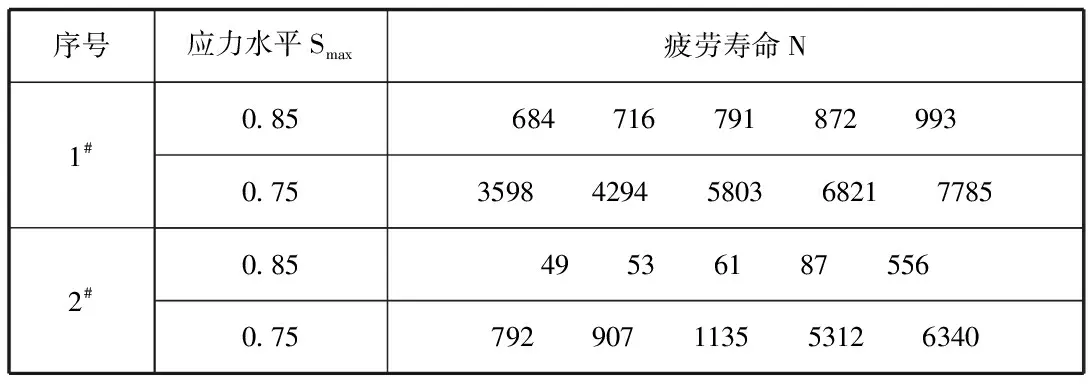
表1　中的混凝土疲劳寿命试验数据

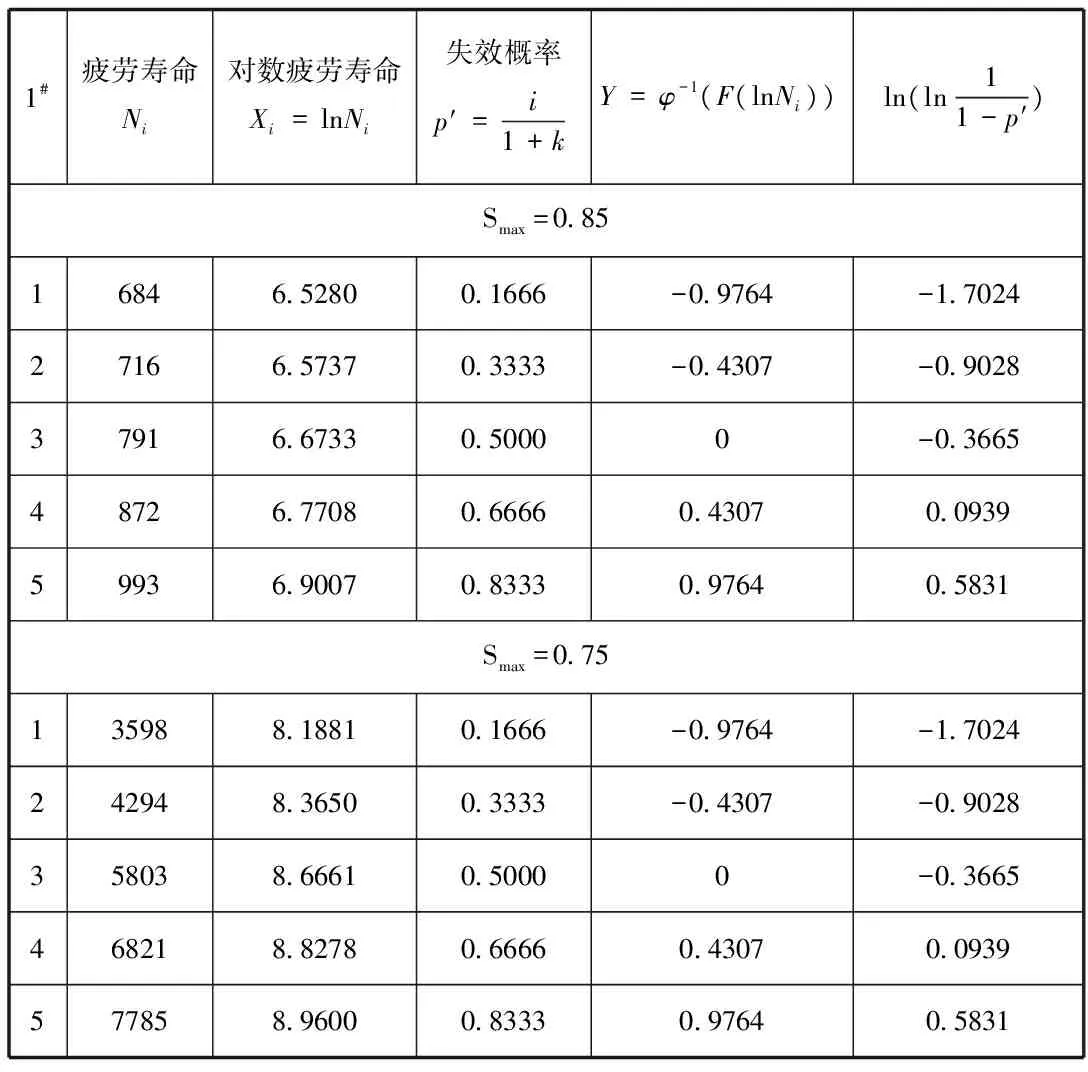
表2　表1中1#混凝土疲劳寿命数据分析

依据表2，并以Xi=lnNi为横坐标，Y=φ-1(F(lnNi))为纵坐标，则产生线性回归检验结果。

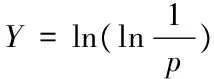
三、结果分析

由对数正态分布线性回归结果可知，函数Y=φ-1(F(lnNi))和Xi=lnNi在各应力水平下均存在良好的线性关系。

经过一系列计算可知，混凝土疲劳寿命既服从双对数正态分布，又服从双对数的双参数Weibull分布。

四、结论

对数正态分布和双参数Weibull分布都可以用来描述混凝土疲劳寿命S-N方程，但后者更敏感于前者对离散数据的变化。其中，具体地用上述两种分析方法的相关系数进行评价时发现，当应力水平较高时，混凝土疲劳寿命数据离散性较大；而当应力水平较低时，混凝土疲劳寿命数据离散性则较小。因此，对于较高应力水平时，在试验过程中，应努力提高试验精度；而在工程评估中，则需偏于保守评价，否则易突发结构安全隐患。

【参考文献】

[1]Xiaoping Chen, Xiaoli Yu, Rufu Hu, etc..Statistical distribution of crankshaft fatigue: Experiment and modeling [J]. Engineering failure analysis, 2014, (42): 210-220.

[2]Luis Saucedo, Rena C. Yu, Arthur Medeiros, etc.. A probabilistic fatigue model based on the initial distribution to consider frequency effect in plain and fiber reinforced concrete [J]. International Journal of fatigue, 2013, (48): 308-318.

[3]郑木莲, 王秉纲, 胡长顺. 多孔混凝土疲劳性能的研究[J]. 中国公路学报, 2004, Vol.17(1): 7-11.

[4]郑瑞君. 多孔混凝土疲劳对比试验研究[J]. 北京交通科技(应用技术版), 2010, (12): 35-37.