耦合调和振子网络系统的分群采样控制同步

万明非，张　华,2，叶志勇，杨　伟

(1.重庆理工大学 理学院， 重庆　400054; 2.铜仁学院 大数据学院， 贵州 铜仁　554300)

近年来网络型调和振子系统的动力学及其协调控制研究由于具有广泛的应用性已被越来越多的国内外学者重视，其中研究最为广泛的是调和振子的一致同步算法。通过研究同步算法，人们不仅可以解释诸如鱼类洄游、候鸟迁徙等自然现象[1-2]，还可以很好地研究如移动机器人的协调控制、并行计算机的负载平衡同步等[3-4]。

学者们提出了许多同步算法来研究调和振子。Ren[5]首次给出了调和振子网络系统的连续时间的耦合模型，在假定网络拓扑结构具有一棵有向生成树的条件下，给出了系统达到同步的条件并得到了系统同步态。Ballard[6]将文献[5]的结果推广到了离散的情况。Su等[7]利用振子间感应距离的概念，认为振子间距离小于一定范围时可以进行信息交换，通过建立适当的控制输入使得每个振子在没有任何连通假设的情况下仍能达到同步。此外，Zhou等[8-9]在无向网络结构中研究了脉冲控制型调和振子和采样控制型调和振子，根据脉冲控制和采样控制的特性，将系统方程演化为一个混杂型的动力学方程，利用拉普拉斯矩阵的分解分析系统的迭代解，得出了系统的同步态和同步的充要条件。Sun等[10]在不考虑控制缺失的情况下将文献[9]中的算法扩展到了有向拓扑结构下。Sun等[11]还利用了随机分析的理论研究了耦合谐振子在耦合时有随机误差的情况。Wang等[12]将耦合时的随机误差推广到了脉冲控制协议下，利用均方收敛的概念得到了系统同步的充分条件，还给出了系统的收敛域。

所有这些工作主要集中在一个完整的网络结构上，且每个网络是连通的或者是含有一棵有向生成树。然而，现实世界中系统的拓扑结构无法固定不变，并且每一时刻都能保持网络连通的条件也十分苛刻，针对这样的问题，Hong等[13]分析了二阶多智能体系统在联合连通下的领导跟随同步问题，唐朝君[14]分析了切换拓扑下离散时间多智能体系统的包含控制。还有一类复杂网络可能由多个子网络组成，它们的合作任务可能被分成几个小组，因此，分群同步能够反应这一本质。在分群同步的研究中，Yu[15]考虑了领导跟随控制下的线性系统的集群同步化，表明如果每个网络拓扑结构都有一个生成树，并且耦合强度足够大，系统可以实现同步。苗中华等[16]在不确定网络的欧拉-拉格朗日系统中研究了分群同步，并且考虑了耦合过程中产生的随机误差，结果表明：系统在一个自适应的控制输入下可以实现分群同步。Zhao等[17]针对2种网络结构研究了脉冲型和连续型调和振子的分群同步。

受到以上工作的启发，本研究将在有向网络拓扑结构下考察耦合调和振子网络系统的分群同步动力学。利用图论中拉普拉斯矩阵的相关引理以及建立适当的误差系统，给出了同步的充要条件。结果表明：在采样周期、耦合强度和拉普拉斯矩阵的非零特征值满足一定不等式关系时，系统能达成分群同步。

1　基础知识和模型建立

1.1　符号说明

R和C分别代表实数集和复数集。N表示自然数集。对任意的c∈C，Re(c)、 lm(c)、|c|分别表示c的实部、虚部、和模。Cn×n代表n阶复矩阵。On∈Cn×n是n阶零矩阵，In∈Cn×n是n阶单位矩阵。对一个n阶矩阵M∈Cn×n，ρ(M)代表它的谱半径，λi(M)表示其第i个特征值。

1.2　代数图论

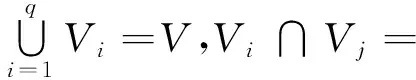
1.3　模型描述

网络型调和振子的动力学行为可以表示为如下形式[5]：

(1)

其中：ri(t)，vi(t)∈R分别表示第i个振子的位移和速度；α>0表示振子的频率；ui(t)表示控制输入。

考虑如下采样控制协议：

(2)

并且假设t∈[tk,tk+1)，tk+1-tk≡T，k∈N。

假设1对每个子群l=1,2,…,q，有∑j∈Vlaij=0，其中i=1,2,…,N，且i∉Vl。

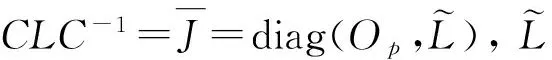
引理2(Schur-Cohn定理)[19]一个复系数二次多项式F(z)=a2z2+a1z+a0，如果它的Schur-Cohn行列式满足：Δ1<0，Δ2>0，则该多项式的根分布在单位圆盘内，其中：

(3)

(4)

2　主要结果

对系统(1)的稳定性进行分析，其详细结果由定理1给出。

定理1当假设1成立时，调和振子系统(1)在控制输入式(2)下达成分群同步的充要条件是：

(5)

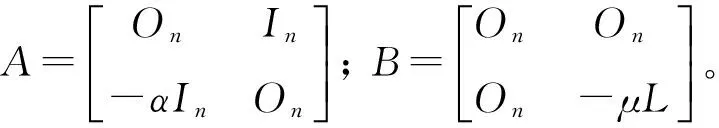
根据引理1做如下变量代换：

e(t)=Cr(t)，s(t)=Cv(t)

则有：

其中：

ei(t)=πir(t),i=1,…,q

…

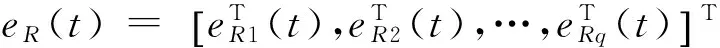
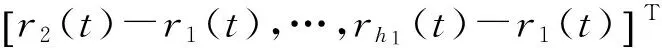
si(t)=πiri(t)，i=1,…,q

…

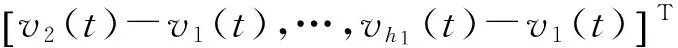
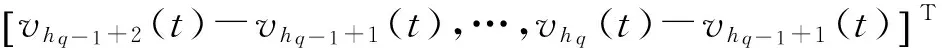
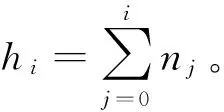
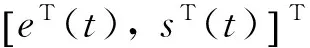
(6)

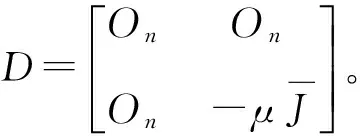
容易看出，方程(6)由下述两类微分方程构成：

(7)

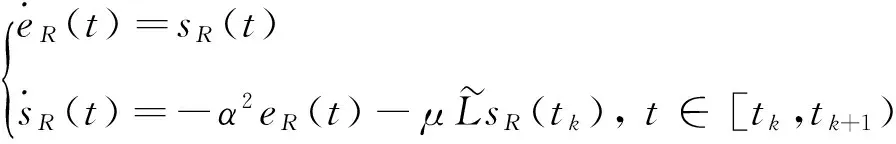
(8)

令x(t)=UeR(t),y(t)=UsR(t)，则有：

(9)

此系统可以被看成由如下2个子系统构成：

当i=nl+1(l=0,1,…,q)时，有

(10)

当i≠nl+1(l=0,1,…,q)时，有

(11)

这里t∈[tk,tk+1)。方程(10)和(11)表明，如果系统(10)渐近稳定，则系统(11)亦渐近稳定。对方程(10)两边从tk到tk+1积分有

(12)

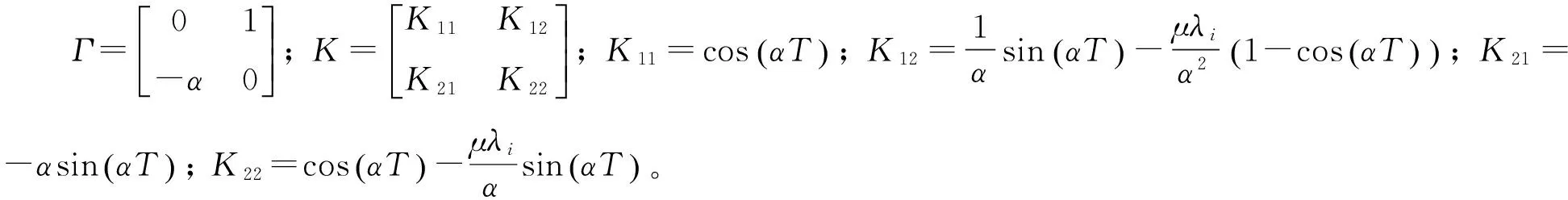
注意到方程(12)是一个离散的线性系统，其稳定的充要条件是ρ(K)<1，下面证明ρ(K)<1，矩阵K的特征多项式为

μλisin(αT)(1-cos(αT))=a2χ2+a1χ+a0=0

根据引理2有：

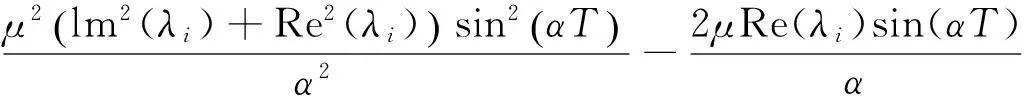
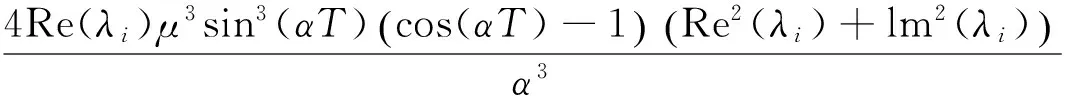
由

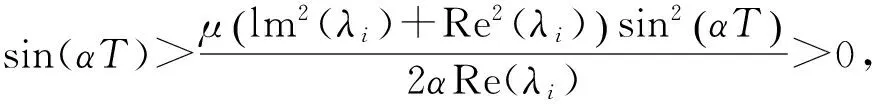
(13)

由

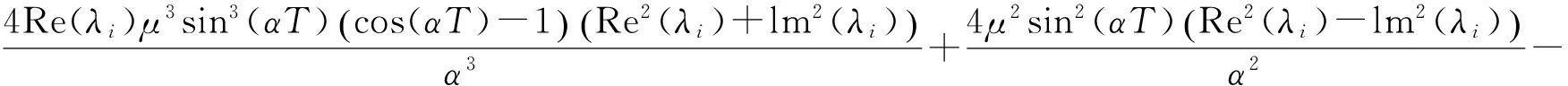
及sin(αT)>0，易知

(Re2(λi)-lm2(λi))-cos2(αT)(Re2(λi)+lm2(λi))+2cos(αT)lm2(λi)+

化简得

(14)

因为式(13)(14)不等号右边具有相同的形式，将两式左端做差可得

故当不等式(14)成立时，不等式(13)亦成立。因此，当且仅当不等式(14)成立时，ρ(K)<1，系统(10)渐近稳定，即系统(1)在控制输入式(2)下能达成分群同步。

3　实验仿真

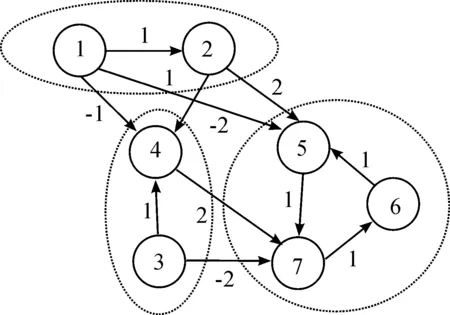
图1　拓扑结构

调和振子在3个子群中的同步时间历程见图2。

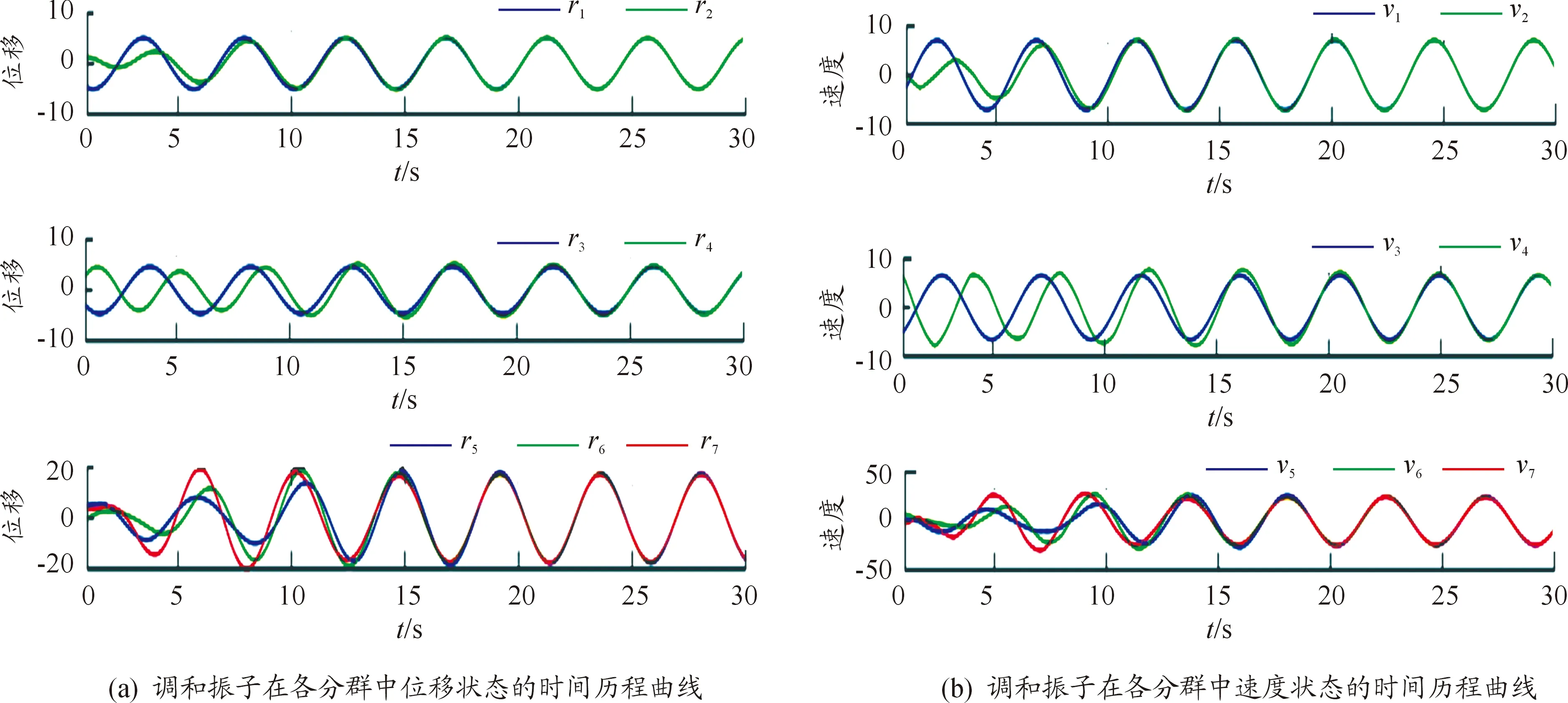
图2　各分群收敛情况(同步时间历程)

4　结束语

基于采样控制下的网络型调和振子模型，分析了系统分群后的一致性问题。利用分群的有向图的拉普拉斯矩阵性质和Schur-Cohn稳定性判据，求出了系统分群同步的充分条件。最后利用Matlab进行数值模拟，进一步验证了结果的有效性。

参考文献：

[1]TONER J,TU Y.Flocks,herds,and schools:a quantitative theory of flocking[J].Physical Review E,1998,58:4828-4858.

[2]REYNOLDS C W.Flocks,herds,and schools:a distributed behavioral model[J].ACM SIGGRAPH Computer Graphics,1987,198:25-34.

[3]BULLO F,CORTES J,MARTINEZ S.Distributed Control of Robotic Networks[M].Princeton:Princeton University Press,2009.

[4]CARLI R,CHIUSO A,SCHENATO L,et al.Distributed Kalman filtering based on consensus strategies[J].IEEE Selected Areas Commun,2008,26:622-633.

[5]REN W.Synchronization of coupled harmonic oscillators with local interaction[J].Automatica,2008,44:3195-3200.

[6]BALLARD L,CAO Y C,REN W.Distributed discrete-time coupled harmonic oscillators with application to synchronised motion coordination[J].IET Control Theory and Applications,2010(4):806-816.

[7]SU H S,WANG X F,LIN Z L.Synchronization of coupled harmonic oscillators in a dynamic proximity network[J].Automatica,2009,45:2286-2291.

[8]ZHOU J,ZHANG H,XIANG L,et al.Synchronization of coupled harmonic oscillators with local instantaneous interaction[J].Automatica,2012,48:1715-1721.

[9]ZHANG H,ZHOU J.Synchronization of sampled-data coupled harmonic oscillators with control inputs missing[J].Systems and Control Letters,2012,61:1277-1285.

[10] SUN W,LU J,CHEN S,et al.Synchronization of directed coupled harmonic oscillators with sampled-data[J].IET Control Theory and Applications,2014,8:937-947.

[11] SUN W,YU X,LU J,et al.Synchronization of coupled harmonic oscillators with random noises[J].Nonlinear Dynamics,2015,79(1):473-484.

[12] WANG J Y,FENG J W,XU C.The synchronization of instantaneously coupled harmonic oscillators using sampled data with measurement noise[J].Automatica,2016,66:155-162.

[13] HONG Y,GAO L,CHENG D,et al.Lyapunov-based approach to multiagent systems with Switching Jointly Connected Interconnection[J].IEEE Transactions on Automatic Control,2007,52(5):943-948.

[14] 唐朝君.切换拓扑下离散时间多智能体系统的包含控制[J].重庆理工大学学报(自然科学),2017,31(5):143-147.

[15] YU J Y,WANG L.Group consensus of multi-agent systems with undirected communication graphs[C]//Proceedings of the 7th Asian Control Conference.China,Hong Kong:[s.n.],2009:105-110.

[16] 苗中华,刘军,王国强,等.随机扰动下不确定网络化Euler-Lagrange系统的分群一致性[J].中国科学:信息科学,2016,46(11):1608-1620.

[17] ZHAO L,LIU J,XIANG L,et al.Group synchronization of diffusively coupled harmonic oscillators[J].Kybernetika-Praha,2016,52(4):629-647.

[18] LIU J,JI J,ZHOU J,et al.Adaptive group consensus in uncertain networked Euler-Lagrange systems under directed topology[J].Nonlinear Dynamics,2015,82(3):1145-1157.

[19] KUO B C.Discrete-data control systems[M].[s.l]:Prentice Hall,1970.