CTS机构几何误差分析及补偿

张竹青，谢志江，蹇开林，缑双双

(重庆大学 机械传动国家重点实验室， 重庆　400044)

获轨迹试验(简称CTS试验)，是研究分离体与母机安全分离特性的一项风洞模拟试验技术。分离体模型6自由度机构(下文简称CTS机构[1])是CTS试验系统的核心，通过控制实现分离体模型6个自由度的运动(X，Y，Z，偏航，俯仰，滚转)。CTS机构的精度是整个CTS试验准确性和可靠性的保障，为提高精度，需要对引起末端位姿误差的各项因素进行分析研究，以达到对末端位姿误差进行补偿的目的，从而提高运动精度。

CTS机构从本质上来说是一个6自由度的机械手[2]。对CTS机构来说，运动精度分为两种[3]：重复定位精度和绝对定位精度。一般情况下，重复定位精度高于绝对定位精度[4]。随着我国综合国力的增强和新型飞行器研制技术的快速发展，对CTS试验也提出了更高的要求[5]。之前研制的CTS机构，由于当时的科学条件限制难以满足当前飞行器研制的需求。近年来，飞行器的研制和改型任务日益繁重[6]，迫切需要研制新型的CTS试验系统，提高其可靠性和相关性能。本课题组研制开发的CTS机构将用于风洞捕获轨迹试验，完成相关的试验项目。

CTS机构的误差补偿采用参数误差直接修正的方法，通常实际参数与理论参数存在差异，从而导致末端执行器产生运动误差。可通过参数标定求出实际参数，然后修改理论值，减小实际值与理论值之间的差异，让运动学模型尽量接近真实情况，最后利用修正过的运动学公式求解驱动值，从而达到减小末端位姿误差的目的。

1　CTS系统坐标系定义

本文对CTS机构误差分析分为两部分：一是机构几何误差分析；二是机构零位误差分析。在误差分析前需要先建立坐标系，在该机构的误差分析及补差过程中涉及风洞固定坐标系、分离体体轴坐标系、天平坐标系和CTS机构总体坐标系。

1.1　风洞固定坐标系Oxdydzd

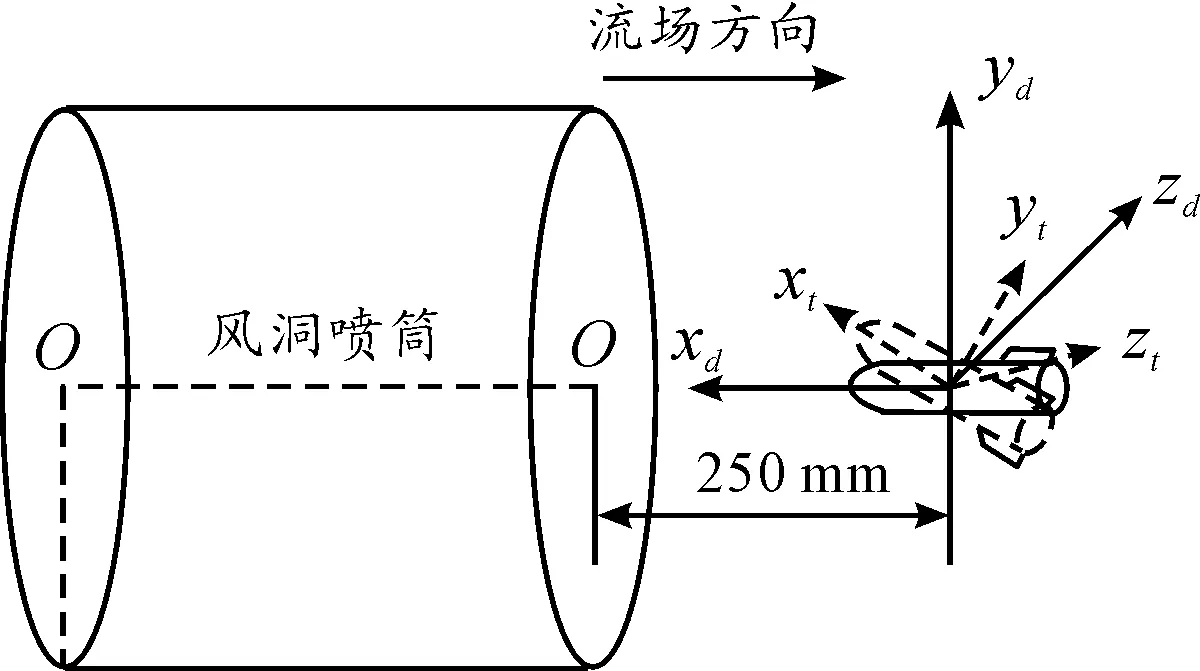
图1　风洞固定坐标系与体轴坐标系定义

风洞固定坐标系Oxdydzd是整个捕获轨迹试验的参考坐标系，不随模型的转动而转动。其原点在风洞喷管端面前250 mm处，位于风洞试验段纵轴上；xd轴沿着试验段纵轴，逆气流方向为正；yd轴位于试验段纵对称平面内，垂直纵轴向上为正；zd轴垂直于纵对称面，从逆气流方向看，向右为正。风洞固定坐标系如图1所示。

1.2　分离体体轴坐标系Oxtytzt

分离体体轴系Oxtytzt的原点位于分离体模型的理论质心。xt轴平行于分离体模型的前行方向；yt轴在分离体模型纵对称平面内垂直于xt轴，方向向上为正；zt轴垂直于分离体模型纵对称面，方向向右为正。分离体体轴坐标系如图1所示。

1.3　天平坐标轴系Oxyz

天平坐标轴系Oxyz是固定在天平上的坐标系。其原点O为天平的力矩参考点；x轴沿天平原点中心线指向模型端；y垂直于Ox轴，在天平纵对称面内，向上为正；z轴可用右手定则确定

1.4　机构总体坐标系Oxzyzzz

机构总体坐标系Oxzyzzz原点O为尾支杆长度为设计长度500 mm处的末端点，总体坐标系不随机构的运动而改变，固定在空间中。沿着尾支杆轴线向外的方向为xz轴正向；yz轴向上为正；zz轴可用右手定则确定。该坐标系与尾支杆等于原长时的天平坐标系重合，当尾支杆长度变化时，天平坐标系会随之改变，而CTS机构总体坐标系的位置不变。

2　CTS机构几何误差分析

给定机构指令位置，逆解求出驱动值，驱动机构运动，则实际位置和指令位置有偏差。需要对机构的转换矩阵Tz调整，使得计算的正解位姿与实际正解位姿尽可能接近。再通过调整后的正解方程反解出逆解方程，给定指令位姿，驱动机构运动，则最终的实际位姿与指令位姿更加接近。

加工几何误差引起的位姿误差值可由式(1)计算。

ΔXz=ΔTzq

(1)

其中：ΔXz代表末端位姿误差列向量；q代表机构输入值，为各驱动滑块滑移距离；ΔTz表示位姿误差矩阵。将式(1)展开成矩阵形式有

(2)

式(2)中ΔT11、ΔT12、ΔT21、ΔT22均为3×3的矩阵。ΔT11表示机构X、Y、Z向导轨与机构总体坐标系的坐标轴线xz、yz、zz轴不平行导致的位置误差矩阵；ΔT12和ΔT22分别表示由机构实际偏航、滚转轴线分别与机构总体坐标系yz轴、zz轴不重合而引起的位置误差矩阵和姿态误差矩阵。为简化误差计算过程，在实际中确定机构总体坐标系时，按照滚转轴线的方向来确定zz轴的方向。ΔT21表示直线滑块驱动引起的姿态角误差矩阵，由于实际中机构位置的变化不会引起姿态角的变化，因此ΔT21为零矩阵。

2.1　导轨与总体坐标系轴线不平行误差分析

理论情况下，实现末端分离体模型平动的3根导轨X、Y、Z分别与机构总体坐标系的xz轴、yz轴、zz轴平行，末端的3个位移是解耦的，因此驱动X向滑块沿着X直线导轨滑移只会引起分离体模型xz向的位移，同理，驱动Y、Z方向的滑块只会引起分离体模型相应方向的位移。但是实际加工出来的机构存在导轨与机构总体坐标轴不平的情况，那么机构末端3个方向的位移与滑块的滑移距离就不再是解耦的，而是相互耦合在一起。分离体模型理论质心3个方向的误差分别设为Δx、Δy、Δz，则将导轨与坐标轴不平行导致的误差写成矩阵形式可表示为

(3)

结合式(2)，有

(4)

这一部分的误差辨识可以考虑用最小二乘法多项式拟合[7]来确定。通过分别测量机构X、Y、Z单轴运动的数据，拟合出驱动滑块滑移距离和分离体模型理论质心位移误差之间的曲线关系，得到拟合函数，即可辨识出导轨与轴线不平行引起的误差矩阵ΔT11。

2.2　偏航和俯仰轴线与总体坐标系轴线不重合误差分析

当偏航和俯仰轴线与机构总体坐标系yz轴或zz轴不重合时，机构绕偏航轴或者俯仰轴运动时，会引起分离体模型理论质心平动的位置误差和绕轴线转动的姿态误差。

2.2.1位置误差分析

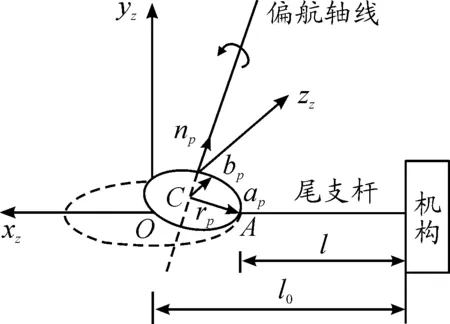
图2　偏航轴线偏移示意图

理想情况下偏航轴线和机构总体坐标系的yz轴是重合的，绕着偏航轴线的偏转，尾支杆末端的天平校心运动轨迹为圆O上的一段圆弧。但实际情况中，由于加工装配误差存在，两轴线不重合，那么机构绕着偏航轴旋转时会引起机构天平校心沿着圆C的圆弧运动，如图2所示。

坐标系Oxzyzzz为机构总体坐标系，尾支杆理论长度为l0，实际长度为l。在理想的情况下，当机构绕着yz轴偏航ψ时，天平校心的理论位置为

(5)

在实际情况中，天平校心运动轨迹所在圆C的圆心坐标为(c1p,c2p,c3p)，法向量为np，半径为rp，对应圆C的参数方程[8-9]为

(6)

其中：(a1p,a2p,a3p)与(b1p,b2p,b3p)分别对应单位向量a和b，它们相互垂直又垂直于np；ψ表示绕着偏航轴yz转过的角度，随着ψ的变化，可以求出实际天平校心在机构总体坐标系中的位置。

偏航轴线偏移引起的天平校心的位置误差值可表示为：

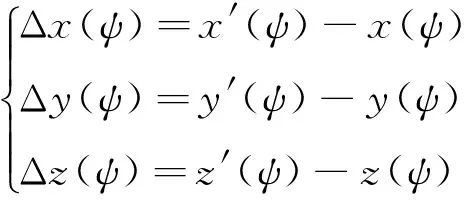
(7)

俯仰轴线偏移对应见图3。

图3　俯仰轴线偏移示意图

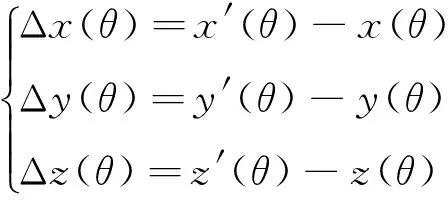
(8)

由于实际机构滚转轴线和机构总体坐标系xz轴线重合，因此机构滚转运动不会引起天平校心位置的运动。

理论偏航角和俯仰角分别是偏航、俯仰驱动滑块滑移距离的函数，即ψ=f(qp)，θ=f(qf)。综上分析，偏航俯仰轴线偏移引起天平校心的位置误差为

(9)

2.2.2姿态误差分析

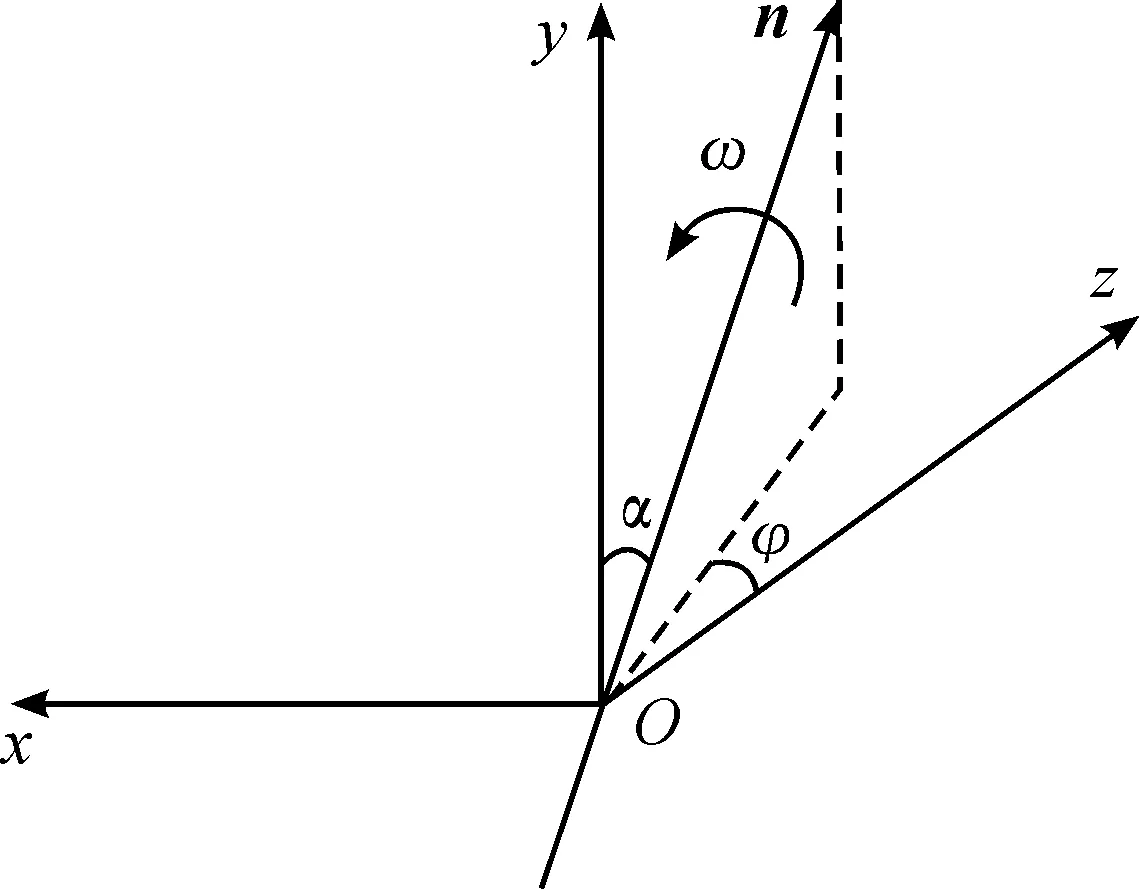
图4　刚体转动示意图

由于偏航、俯仰轴线与机构总体坐标系的yz轴、zz轴有微小的倾角，因此偏航轴线的偏航运动实际上会引起分离体模型在机构总体坐标系中偏航、俯仰和滚转，俯仰时相同。

机构实际绕偏航、俯仰轴运动时，相当于已知了偏航、俯仰轴的轴线方向以及转角大小，然后求解分离体模型在总体坐标系转过的角度。

任意个刚体的转动可以用定轴转动的转轴转角参数(球坐标)来描述，也可以使用姿态角来描述。那么轴线偏移对应的情况是已知分离体模型的转轴转角参数求解姿态角。

如图4所示：n表示实际轴线方向的单位矢量；ω为转过的角度；(α,φ)为矢量n的球坐标角。转动R球坐标描述为

(10)

其中：

cω=cosω,sω=sinω,cφ=cosφ,sφ=sinφ,cα=cosα,sα=sinα

转动姿态角描述为

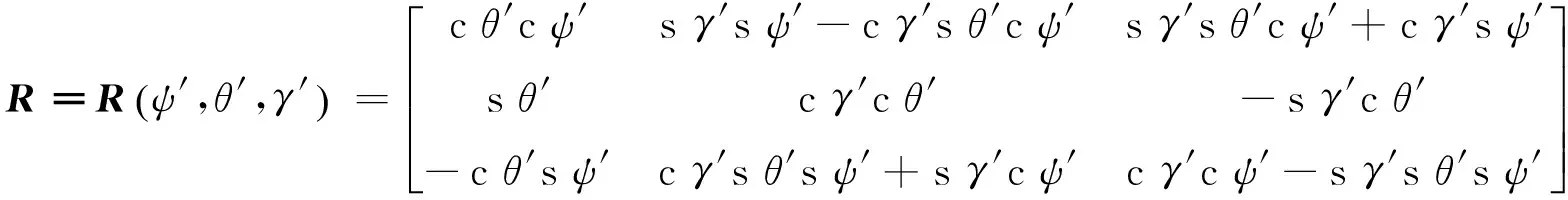
(11)

其中：

cθ′=cosθ′,sθ′=sinθ′,cψ′=cosψ′,sψ′=sinψ′,cγ′=cosγ′,sγ′=sinγ′

由式(10)与(11)中的元素对应相等求出实际的ψ′、θ′、γ′。

对于偏航轴线与yz轴不重合引起的误差为

(12)

对于俯仰轴线与zz轴不重合引起的误差为

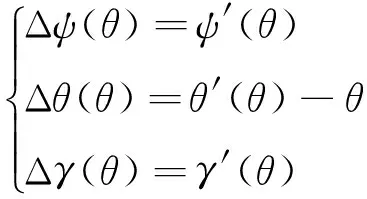
(13)

因此，由偏航和俯仰轴线与机构总体坐标系轴线不重合引起的姿态误差可表示为

(14)

2.3　机构零位误差分析

采用CTS机构运动学方程求分离体模型位置和姿态与CTS机构驱动滑块滑移距离之间的关系，分离体模型的位置和姿态必须放在特定的坐标系中。在理想情况下，风洞坐标系与CTS机构总体坐标系重合。

在实际情况中，风洞固定坐标系是通过喷管的位置确定的，机构总体坐标系是由机构确定的，这2个坐标系不会完全重合，即当CTS机构未运动处于机构零位时，分离体模型在风洞固定坐标系中的位姿已经有初值，所以在误差补偿时需要对机构的零位进行补偿。

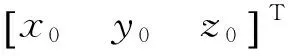
3　机构几何误差补偿试验研究

3.1　数据采集与处理

3.1.1单轴运动数据测量与分析

针对加工好的机构，需要对机构单轴运动时的重复定位精度和绝对定位精度进行测量。对长度为500 mm的尾支杆，末端固定粘贴一个靶标，单轴运动，利用激光跟踪仪测量点的位置，在计算机测量软件中记录下来。X、Y、Z方向每100 mm记录1个点的数据，由于数据量很大，在此就不一一列出。

按照设计，单轴驱动X滑块时，末端测量点的yz和zz不应产生位移值，则实际产生的位移值也就是Y和Z方向的误差值，用δx(qx)、δy(qx)、δz(qx)分别表示单轴驱动X方向运动时对X方向、Y方向、Z方向产生的误差值。此处将测量数据利用Matlab绘制出误差曲线，如图5～9所示，图中δj(qi)表示驱动i方向的滑块引起的jz方向的位移误差。单轴驱动Y和Z方向时同理。

通过数据分析，可得到CTS机构单轴运动时各轴的重复定位精度和绝对定位精度值，见表1和表2。

图5　X滑块滑动引起质心xz向位移误差

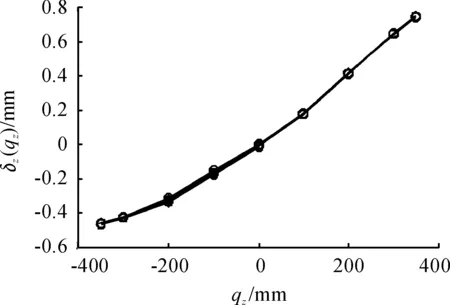
图7　Z滑块滑动引起质心zz向位移误差

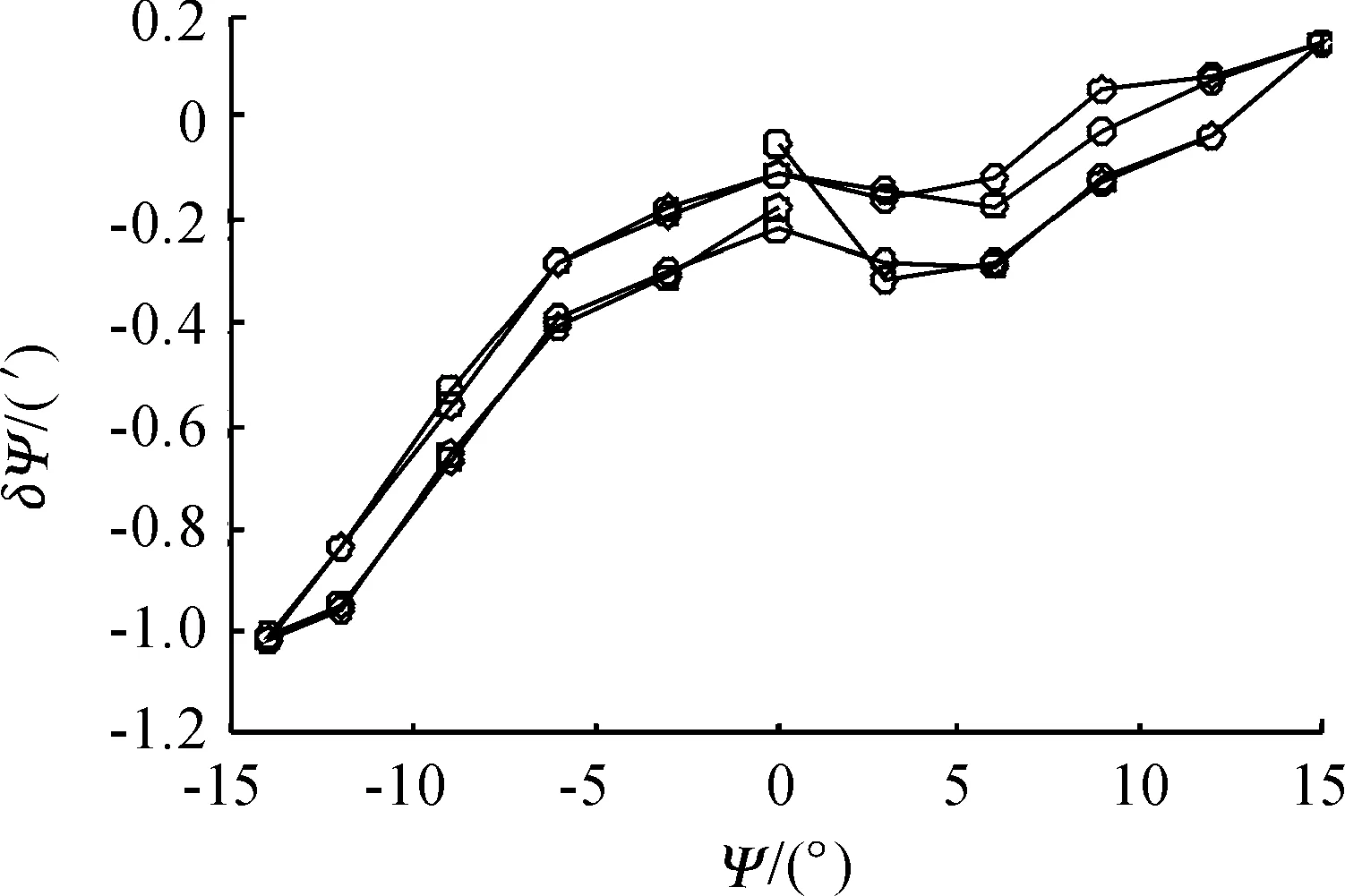
图9　偏航角度误差值

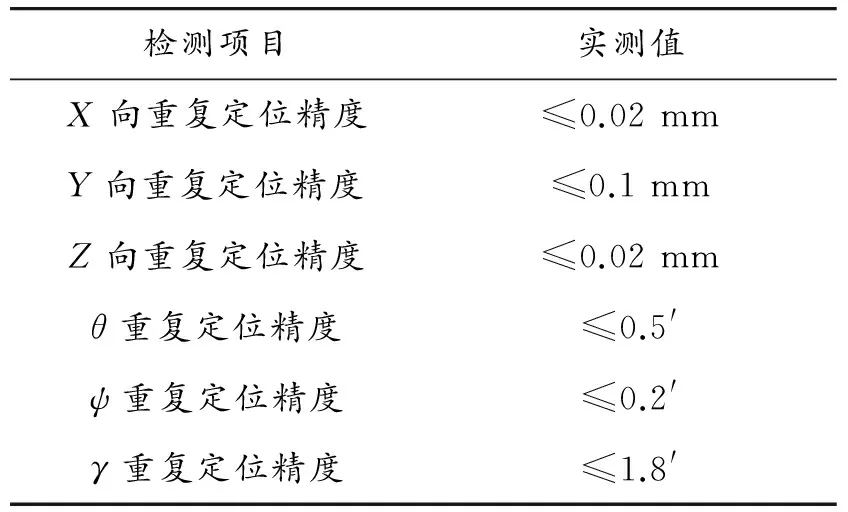
检测项目实测值X向重复定位精度≤0.02mmY向重复定位精度≤0.1mmZ向重复定位精度≤0.02mmθ重复定位精度≤0.5'ψ重复定位精度≤0.2'γ重复定位精度≤1.8'

表2　CTS机构绝对定位精度

将表1中的测量值和允许值比较，只有滚转角γ的重复定位精度不够，其原因主要是测量方法本身引起的误差过大。测量时，靶标贴在尾支杆安装端面上，在滚转电机驱动下，靶标开始转动，通过前后2次运动靶点的位置坐标来计算滚转角。这种测量方式由于靶点经过的圆弧太小，测量数据的测量误差对计算出的滚转角影响较大，因此需要改进测量方法，增大滚转的圆弧半径。

将表2测量值和允许值比较，单轴驱动时只有Z向的定位精度不满足要求。考虑各项误差产生的运动误差的累加效应，仍需对单轴驱动进行误差补偿。

3.1.2零位测量

在建立好风洞固定坐标系和CTS机构总体坐标系后，进一步可以通过激光跟踪仪测量和计算出机构总体坐标系的初始零位，初始零位位姿见表3。表3中：x0、y0、z0表示机构总体坐标系在风洞固定坐标系中的位置；ψ0、θ0、γ0表示从风洞固定坐标系旋转到机构总体坐标系的姿态角。

表3　初始零位位姿

3.2　误差补偿

数据测量完后需要对补偿效果进行验证。在正逆解程序中加上零位，给定末端点在风洞固定坐标系中的位姿，控制器驱动机构运动到实际位姿，利用激光跟踪仪测量实际位姿，计算补偿前定位误差；将控制器中的程序改为补偿后的程序，给定同样的位姿，测量机构达到的位姿，计算补偿后的定位误差；前后对比，验证补偿效果。

机构单轴误差可由上述方法来标定，由于测量数据重复性比较好，可以采用最小二乘法多项式拟合求出误差函数。单轴运动误差拟合曲线见图10～12，图中横坐标表示滑块滑移距离，纵坐标δj(qi)表示驱动i方向的滑块滑动引起的质心在总体坐标系中jz方向的位移误差值。

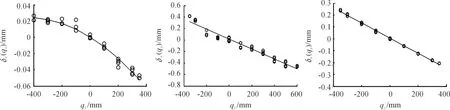
图10　δx(qi)误差拟合曲线

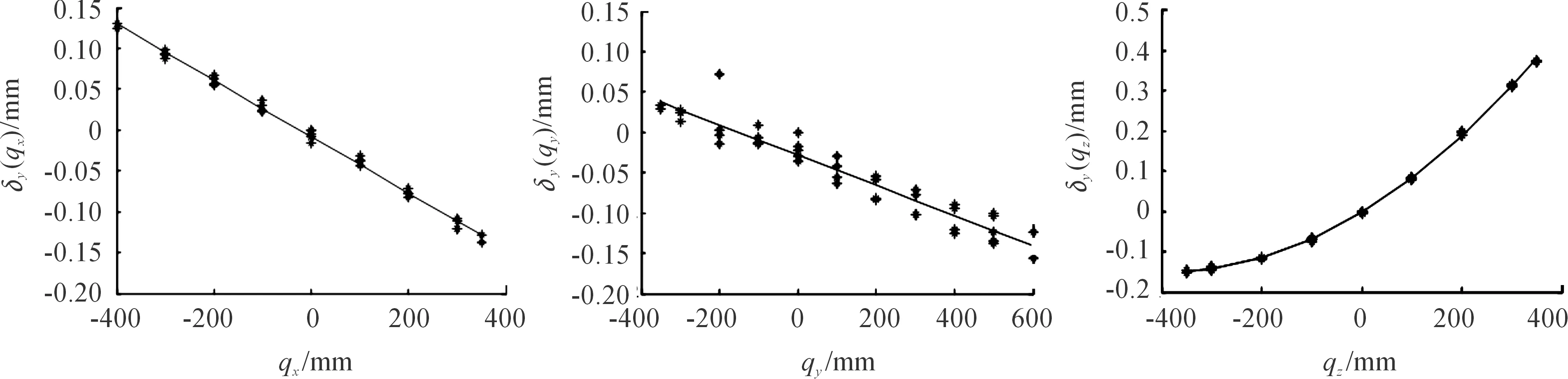
图11　δy(qi)误差拟合曲线

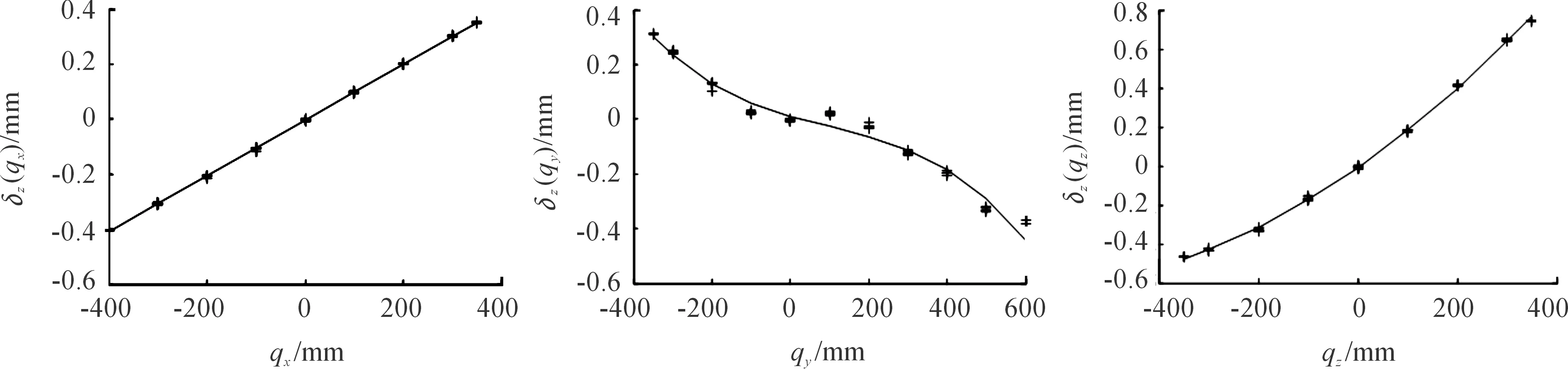
图12　δz(qi)误差拟合曲线

通过最小二乘法拟合出的误差曲线图对应的误差函数分别如下：

(15)

(16)

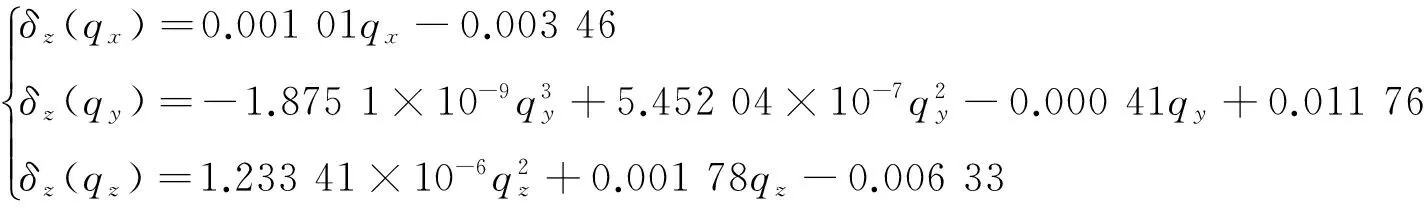
(17)

那么，式(3)中的导轨与轴线不平行而导致的误差为

(18)

机构三轴联动误差在CTS机构总体坐标系原点处，因此将式(18)以及测试出的机构总体坐标系和风洞固定坐标系之间的零位数据代入相应正解方程中，便可得到补偿后的正解。

补偿后的逆解需要通过正解方程反求输入的滑块位移，过程为求解3个三元方程组成的非线性方程组，将方程组写成一般形式编入CTS机构控制器软件中，同时添加求解非线性方程组的牛顿迭代法[10-11]，即可完成CTS机构逆解的求取。

图13　三轴联动补偿前后绝对定位精度对比

为了验证误差补偿的结果，通过测量X、Y、Z三轴联动来检测导轨与机构总体坐标系轴线不平行的误差方法的有效性。

未补偿前，给定空间15个点的位置，通过控制软件中的逆解程序计算并驱动机构运动，记录最终模型理论质心在风洞固定坐标系中的位置(已补偿零位)，将给定位置和最终达到的位置记录下来。给定同样的位置，利用补偿后(补偿零位及导轨与轴线不平行误差)的逆解驱动机构运动，将补偿后实际到达的位置记录下来。根据2次的记录，计算出补偿前后的定位误差，如表4所示，将补偿前后的定位误差绘制成曲线图，如图13所示。

由图13可知：CTS机构的3轴联动绝对定位精度得到了明显的提高，补偿前绝对定位误差的最大值为0.952 2 mm，补偿后绝对定位误差的最大值为0.112 3 mm，绝对定位精度提高了88.21%。

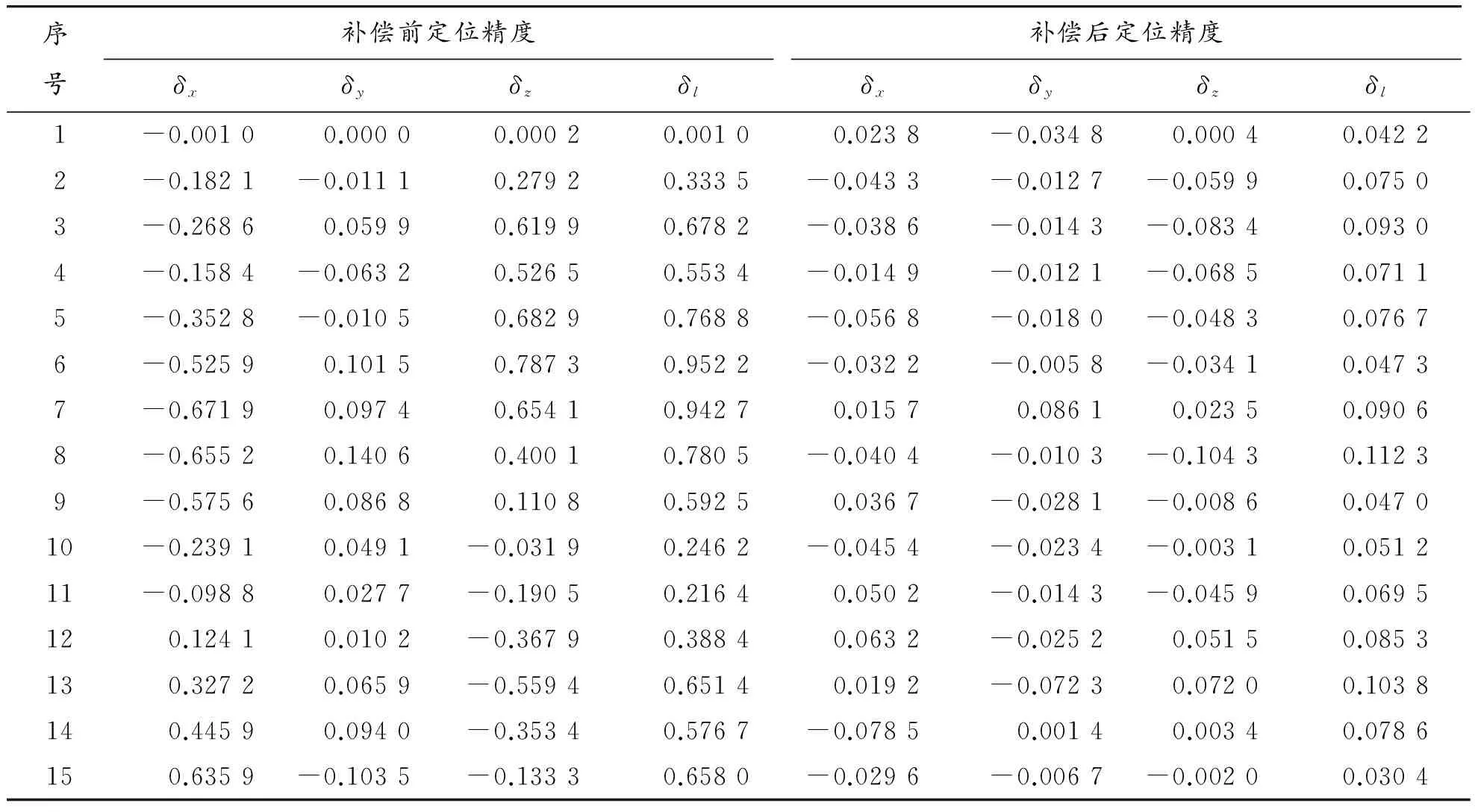
表4　三轴联动误差补偿前后绝对定位精度(mm)

4　结束语

本文对CTS机构的几何误差进行了详细的理论分析，通过实验测试得到数据，并采用最小二乘法拟合辨识了导轨与轴线不平行引起的运动误差，通过理论分析求解了偏航俯仰轴线偏移的误差矩阵，将辨识出的误差矩阵引入到正解方程中，得到补偿后的正解方程。利用牛顿迭代法求取补偿后的正解方程组成的非线性方程组，得到补偿后的逆解。通过对补偿试验现场测量相关数据的分析，利用本文研究的补偿方法，采用软件补偿法完成了CTS机构的几何误差补偿。通过X、Y、Z三轴联动比较了补偿前后CTS机构的定位误差，验证了补偿方法的可靠性。

参考文献：

[1]缑双双，蹇开林.一种六自由度分离体机构运动学分析及仿真[J].重庆理工大学学报(自然科学)，2017，31(5)：43-48.

[2]YOSHIKAWA J.Manipulability of Robotic Mechanisms[J].Int J Robotics Reserch，1987，4(2)：3-9.

[3]王东署，迟健男.机器人运动学标定综述[J].计算机应用研究，2007，24(9)：8-11.

[4]王东署.工业机器人标定技术研究[D].沈阳：东北大学，2006.

[5]黄叙辉，罗新福.FL-24风洞新型捕获轨迹系统设计与发展[J].空气动力学报，2008，26(2)：145-149.

[6]黄叙辉，庞旭东，等.1.2 m跨超声速风洞新型捕获轨迹系统研制[J].实验流体力学，2008，22(2)：95-98.

[7]李蓓蕾.多次自适应最小二乘曲线拟合方法及其应用[D].荆州：长江大学，2014.

[8]路元鸿.三维空间中圆的参数方程[EB/OL].[2017-03-08].http://www.mathchina.net/dvbbs/dispbbs.asp?boardid=3&Id=471.

[9]李养成，郭瑞芝.空间解析几何[M].北京：科学出版社，2004.

[10] 王开荣，杨大地.数值分析[M].北京：高等教育出版社，2010.

[11] 徐建强.并联机构中常用的数学分析法[J]. 农业装备技术，2010(5)：20-21.