融合用户自然最近邻的协同过滤推荐算法

王　颖，王　欣，唐万梅

WANG Ying,WANG Xin,TANG Wanmei

重庆师范大学 计算机与信息科学学院，重庆 401331

College of Computer and Information Science,Chongqing Normal University,Chongqing 401331,China

1　引言

互联网技术、设备和网络资源的逐步发展和日趋丰富使人们的日常生活与Internet的关系愈来愈密不可分。CNNIC报告显示，我国网民数量截至2016年6月已达7.10亿[1]。网络信息过载和信息迷航等问题成为众网民获取想要信息以及得到个性化推荐的需求无法满足的主要原因，这种情况下，推荐系统通过分析用户行为，向不同用户提供更准确的个性化推荐越来越迫切。

推荐系统作为一种基于用户网络行为信息向用户提供与其行为相关信息的信息预测与交付系统[2-5]，目前已被广泛应用于电影、音乐、阅读、电商、广告、社交网络、新闻媒体、基于地理位置的推荐、个性化邮件等多个领域[6]。作为推荐系统最普遍采用的算法，基于用户近邻的协同过滤推荐的基本原理是通过寻找与目标用户兴趣相似的用户集合即近邻用户，向目标用户推荐近邻用户喜欢且目标用户未评分过的物品。如，某推荐系统中存在任意用户A及与其兴趣相似的邻居用户B、C、D，假设B、C、D用户看过电影《阿甘正传》且对该电影评分较高，而A用户未看过《阿甘正传》，则推荐系统根据A和B、C、D的邻居关系，向A推荐《阿甘正传》这部电影。任何推荐都应该伴随合理的推荐解释，即为何这样推荐[7-8]，而基于用户近邻推荐，具有较强解释性。此外，基于用户近邻的推荐具有实现相对简单，可解释性强，高效、稳定等显著的优越性[9]。目前常用的近邻方法有：KNN、K-means、K-d Trees、LSH等。

传统的KNN使用预先固定的K值，没有充分利用数据集的重要信息，如训练集中每个样例的维数大小[10]。进行推荐时，固定的K值会使目标用户偏向训练集中拥有较多评分的用户，结果造成倾向于向目标用户推荐拥有较多评分的邻居喜欢的项目。选取不同K值会造成推荐结果具有不确定性，且得到最优K值通常需要迭代方法，计算量较大，通常采用off-line的方式进行。而K-d Tree面临的维数灾难降低了算法的有效性。相关学者纷纷提出对基于K近邻推荐算法的改进方法，如罗辛等[11]提出一种通过相似度支持度优化K近邻模型的方法，选择合理规模的K近邻，保持推荐精度前提下降低计算的复杂度。考虑到用户近邻的分布不均匀和对分类贡献的不同以及避免仅由评分决定K近邻带来的片面性，尹航等[12]提出了用各个样本与其所属类别的类别关联度来区分对待待预测用户的K个最近邻居，达到提高推荐精度的目的。黄创光等[13]提出了一种不确定近邻的协同过滤推荐算法（Uncertain Neighbors Collaborative Filtering，UNCF），根据用户及产品的相似性自适应地获取目标用户近邻作为推荐群，在推荐群基础上得到目标用户的信任子群，再使用一种不确定近邻因子度量推荐结果。更多文献是从相似度的角度进行优化，利用用户的多种信息如评分值和共同评分项目的个数等进行改进，并一定程度上提高了推荐准确度[14-15]。以上方法虽然一定程度上提高了推荐效果，但存在以下不足：（1）都是通过分析目标用户寻找近邻，而忽略了邻居用户的分析，形成一种不对称的邻居关系。（2）没有充分利用隐藏邻居用户的信息。（3）都是在选择近邻前通过聚类或设置相似度阈值u、v筛选邻居，或者选出K近邻后通过贡献度、相似度、类别关联度等改进邻居关系，算法涉及近邻数K、相似度阈值u和v、聚类的类别关联度等多个参数，参数设置不同对推荐结果有影响。

自然最近邻概念于2011年首先由Zou等[16]提出，这是一种去参数的、对称的邻居关系，考虑到了空间分布疏密程度对近邻个数和邻居对称关系的影响，简单且容易实现，目前已经被改进和应用到多方面[17-19]，尤其在聚类、分类和离群点检测等方面表现颇佳。本文在此基础上，提出一种融合用户自然最近邻的协同过滤算法（Collaborative Filtering recommendation integrating user-centric Natural Nearest Neighbor，CF3N）。本文算法试图在K近邻的基础上，去参数K，自适应地获取目标用户的自然近邻集合。在评分预测时充分考虑到邻居用户对评分预测的贡献，将目标用户关于目标项目的活跃邻居集合与自然最近邻用户集合融合后形成推荐邻居集合，并根据推荐邻居集合预测评分，计算RMSE和MAE值得到评分预测的准确度。通过在MovieLens数据集上进行仿真实验，验证本文算法在复杂程度和推荐准确度方面较传统基于K近邻的协同过滤推荐算法具有一定的优越性。

2　传统的基于近邻的协同过滤算法

传统的基于近邻的协同过滤算法分为基于用户近邻的协同过滤推荐和基于项目近邻的协同过滤推荐两个方面。目前，大多数推荐系统使用的是基于项目近邻的推荐算法，如Netflix、Amazon等网站，因为该方法更注重用户的历史兴趣且推荐系统中用户总数往往大于项目总数，从存储角度来看更有优势，但对于个性化不太明显且项目更新较快或数量庞大的领域则不太适合。传统的基于用户近邻的协同过滤具有更长的发展历史，第一个邮件过滤系统Tapestry、Digg网站的个性化阅读、GroupLens的个性化新闻推荐都是使用的该方法，因为新闻、文章、图书更新速度快且数量远超用户数，人们对于“新”的需求超过了对“个性化”的需求，此时该方法在存储代价、推荐速度、实现的难易程度等方面具有更强的优势。此外，实际应用中基于用户近邻的协同过滤方法相比基于项目近邻的协同过滤在推荐结果的召回率、覆盖率、新颖度等方面表现更优[6]。虽然该方法在解决用户冷启动问题时表现不佳，但仍然具有独特的优势和较强的应用价值。

传统的基于用户近邻的推荐算法主要工作包含：（1）建立用户-项目评分矩阵；（2）计算用户之间关于评分的相似度；（3）建立用户-用户相似度矩阵；（4）寻找与目标用户最相似的邻居对目标用户进行评分预测；（5）计算评分预测的准确度。具体步骤如下。

2.1　建立用户-项目评分矩阵

假设推荐系统中存在m个用户，n个项目，用户集合表示为U={user1,user2,…,userm}，项目集合表示为I={item1,item2,…,itemn}，评分矩阵表示为 R=[r1,1,r1,2,…,r1,n;r2,1,r2,2,…,r2,n;…,rm,1,rm,2,…,rm,n]，其中 R 矩阵中评分值范围在1～5之间（0表示无评分），建立如下用户-项目（User-Item）评分矩阵（如表1）。

表1　用户-项目评分矩阵

2.2　根据评分值计算用户之间相似度

传统的基于用户近邻推荐算法采用的相似度计算方法主要有以下几种：

（1）Cosine相似度

余弦相似度（公式（1））表示目标用户u及其邻居用户v的评分向量之间的夹角余弦值，余弦相似度的范围值在[－1，1]区间，1表示两个用户完全相似，0表示两用户相互独立，－1则表示两用户完全不相似。

（2）Pearson相似度

Pearson相似度（公式（2））取值在[－1，1]之间，负数表示两用户负相关，正数表示两用户正相关，0表示两用户不相关。其中，Iuv表示目标用户u和邻居用户v共同评分过的项目集合，rui表示用户u对项目i的评分，表示用户u对所有评分过的项目的评分均值。

（3）Jaccard相似度

Jaccard相似度（公式（3））表示集合 Γ(u)和 Γ(v)中相同元素个数除以Γ(u)和Γ(v)并集中的元素个数，其范围在[0，1]之间。Jaccard相似度适合两极评价，如音乐评价中判断用户是否收藏了歌曲，用户u和v收藏的歌曲的交集除以并集，得到的Jaccard相似值可以反映两用户的相似度。而不适合多级评价，如1～5分5个等级的评价方式。

2.3　寻找目标用户u的K近邻集合

假设推荐系统中用户的兴趣是相对稳定的，且兴趣越相似的用户越倾向于喜欢相同的项目。把用户集合U中的用户按照与目标用户的相似度由大到小即Sim值降序排序，Sim值越大表示该用户与目标用户兴趣越相似，则该用户越有可能与目标用户喜欢相同的项目。找出Sim值最大的前K个用户，即与目标用户最相似的或最近的K个邻居，这K个用户组成目标用户u的K近邻集合Neighbor(u)。其中，目标用户的邻居个数K值大小是由算法设计者自主选取，不同的K值对推荐结果准确性有影响。

2.4　对目标用户u进行评分预测

根据目标用户的邻居即集合Neighbor(u)中用户的评分值和相似度，预测目标用户u对目标项目i的评分，评分预测公式（公式（4））如下：

2.5　推荐结果准确性评测

目前，推荐算法的评测指标主要从用户、物品、时间三个维度进行，包括用户满意度、预测准确度、覆盖率、多样性、新颖性、惊喜度、信任度、实时性、健壮性、商业目标是否达成等多个指标[6]，然而预测准确度依然是协同过滤最重要的指标[9]。预测准确性又包含评分预测准确性方面的平均绝对误差（MAE）和均方根误差（RMSE）两个指标。

3　融合用户自然最近邻的协同过滤推荐

传统的基于用户K近邻的协同过滤推荐算法通过计算用户相似度再按照相似度值由大到小把邻居排序后，直接选取与目标用户距离最近的K个用户作为目标用户的邻居集合，没有考虑到邻居的对称性且K值的选取方法不同对评分预测结果的准确性影响较大。常用方法是选择特定步长，计算不同K值下的用户评分预测结果及其准确性，直到推荐准确率达到设定的阈值为止。而这种方法无疑计算量较大，实现起来相对复杂，且准确率不高。

本文着眼于用户近邻集合的选择，充分考虑到传统基于用户K近邻的协同过滤推荐算法以上所述不足之处，提出了一种融合用户自然最近邻的协同过滤推荐算法。在确定推荐邻居集合时，首先找到目标用户u的自然最近邻居集合（定义1）NaturalNearestNeighbor(u)和目标用户u关于项目i的活跃用户集合（定义2）ActiveNeighbor(u,i)，将二者融合后的结果作为待预测用户u关于项目i的推荐邻居集合RecommendNeighbor(u,i)，根据推荐邻居集合预测目标用户u的评分r̂(ui)。本文推荐算法流程如图1所示。

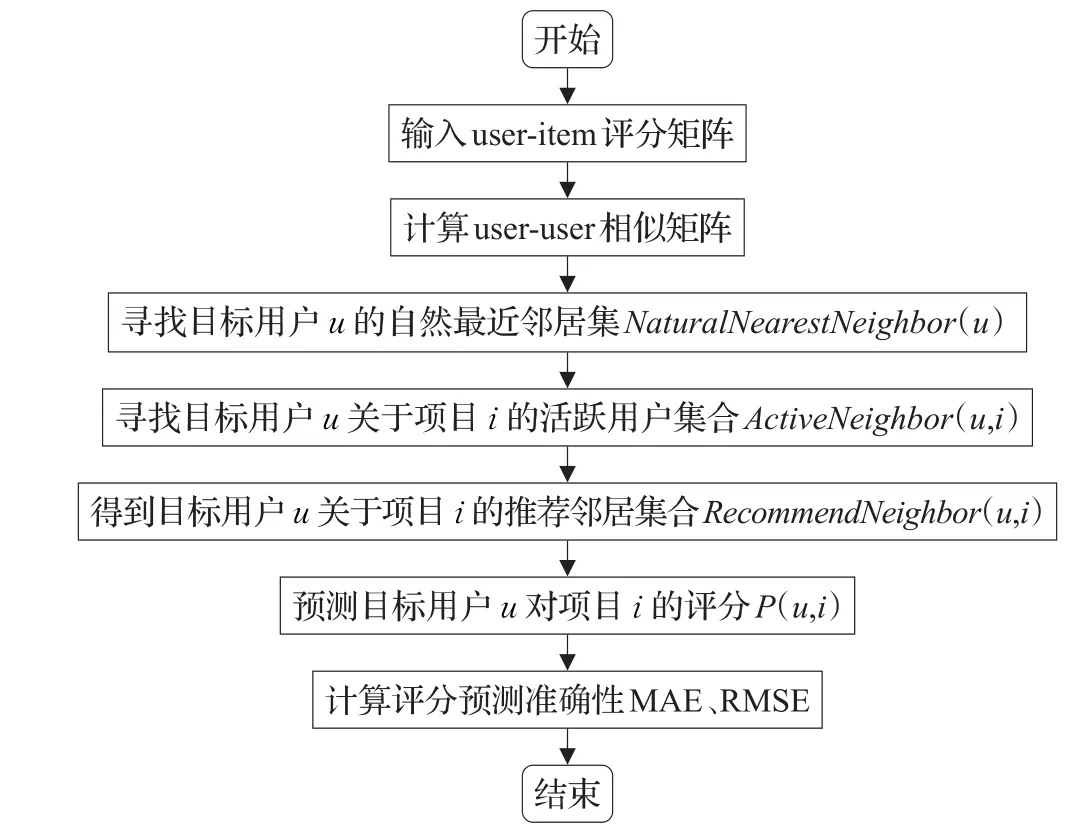
图1　CF3N算法流程图

3.1　前提工作

CF3N是一种新的改进的基于用户近邻的推荐算法，该算法中用户近邻个数不需要提前设置好，而是在算法过程中自适应生成。可以将任意用户u看作空间里的一个点，推荐系统中存在的大量用户U构成一个点空间，空间中两个用户距离越近则相似度Sim值越大，称这两个用户的兴趣偏好越相似。不难理解，空间分布密集区域的用户群具有更多的自然最近邻居，分布稀疏区域的用户具有较少的自然最近邻居。

假设有给定的用户集合U={user1,user2,…,userm}，用户u，v∈U ，项目集合I={item1,item2,…,itemn}，项目 i∈I。用户的评分矩阵表示为 ScoreMatrix（m×n）=

u和v的相似度，Simu,v的值越大则表明用户u和v对项目（如电影）的品味越相近。按照相似度值由大到小排序后，得到邻居矩阵 NeighborMatrix（m×(m-1)）=

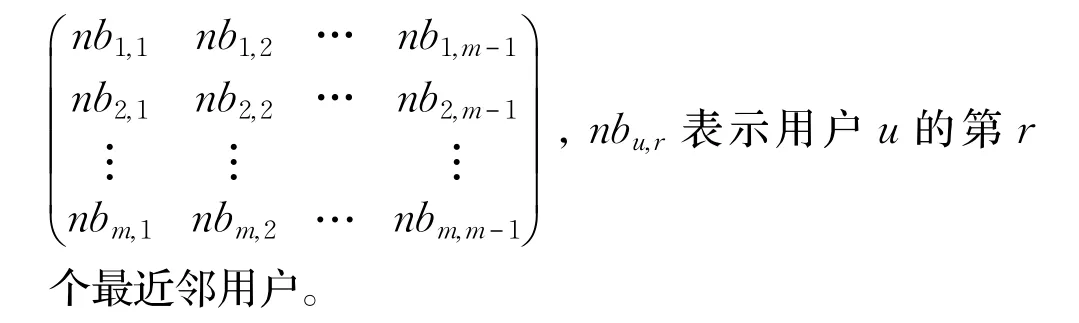
3.2　获取推荐邻居集合RecommendNeighbor(u,i)

在向目标用户u推荐时选择的邻居个数随用户分布疏密程度有所不同，即NaturalNearestNeighboradpt_r(u)集合的大小与u所处空间用户疏密程度呈正相关。因为现实中的推荐系统数据稀疏度往往会高达90%以上，在预测目标用户u对目标项目i的评分时，其自然最近邻NaturalNearestNeighboradpt_r(u)中的邻居用户并非全部都是活跃用户，非活跃用户在评分预测中所起作用不大，此时采用融入活跃用户集合的方法，把NaturalNearestNeighboradpt_r(u)和 ActiveNeighbor(u,i)融合后的结果作为评分预测时使用的邻居集合Recommend-Neighbor(u,i)，具体步骤如下。

3.2.1获取正最近邻用户集合NearestNeighborr(u)

对于推荐系统中的用户空间U，依次寻找所有用户的第一正最近邻、第二正最近邻……直到U中的每个用户都出现在其他用户的正最近邻集合里时，共进行了r次查询，即每个用户的第r正最近邻居。此时，得到的用户u的r近邻集合则为用户u的正最近邻集合。寻找正最近邻算法如下（CodeⅠ）：

可知，r∈[1,m-1]，当存在一个用户离群比较远时，即该用户是其他每一个用户的最远邻居时，最坏情况下需要查询m-1次后才满足终止条件“每个用户都是其他用户的正最近邻”，会造成算法的搜索长度大大增加，这种情况下可以设置一个阈值ϕ∈(0,1)，当r＞ϕ·m时即停止搜索。

3.2.2获取逆最近邻用户集合ReverseNearestNeighboradpt_r(u)

CF3N协同过滤推荐算法选择用户近邻时，考虑到的邻居关系是一种对称关系的邻居，如目标用户u有r个正最近邻，若反过来用户u出现在其r个邻居的正最近邻集合中至少一次，则才能构成对称的邻居关系。寻找目标用户u的逆最近邻用户算法如下（CodeⅡ）：

3.2.3获取自然最近邻用户的集合NaturalNearest-Neighboradpt_r(u)

定义1（用户u的自然最近邻居集合）已知目标用户u的正最近邻用户集NearestNeighborr(u)，以及用户u的逆最近邻用户集ReverseNearestNeighboradpt_r(u)，若存在任意用户v，满足v∈NearestNeighborr(u)⋂Reverse-NearestNeighboradpt_r(u)，称用户v为用户u的自然最近邻[17]。

确定用户的正最近邻用户集NearestNeighborr(u)和逆最近邻用户集ReverseNearestNeighboradpt_r(u)后，可通过计算两个集合的交集得到用户的自然最近邻居集合NaturalNearestNeighboradpt_r(u)。自然最近邻居集合避免了传统基于K近邻算法只考虑邻居用户兴趣而忽略了分析目标用户兴趣的缺点。邻居用户的兴趣和目标用户u相近，同时目标用户u的兴趣与其邻居用户兴趣相似时，得到的才是全面的、对称邻居关系的用户集合。用户u的自然最近邻居集合（定义1），操作过程如下（CodeⅢ）：

3.2.4获取用户u关于项目i的活跃邻居用户集合ActiveNeighbor(u，i)

定义2（用户u关于项目i的活跃邻居用户集）已知目标用户u的邻居集合NeighborMatrix(u)，任意用户m∈NeighborMatrix(u)，如果rm,i≠0，则称用户m为用户u关于项目i的活跃邻居用户。满足rm,i≠0的用户集合则为用户u关于项目i的活跃邻居用户集合，即ActiveNeighbor(u,i)。

目标用户u的自然最近邻用户集NaturalNearest-Neighboradpt_r(u)中可能存在未对项目i评分的邻居用户，根据评分预测公式（5）可知，在预测用户u对项目i的评分时只有对项目i评分过的邻居才是真正贡献最大的用户，把那些对目标项目i评分值为非0的用户称作目标用户u关于项目i的活跃用户集合ActiveNeighbor(u,i)，获取活跃邻居用户集的方法如下（CodeⅣ）：

3.2.5获取推荐集合RecommendNeighbor(u,i)

传统的基于K近邻的协同过滤算法直接选取与目标用户相似度最高的前K个用户作为邻居用户进行评分预测，容易忽略掉真正对评分预测有意义的用户。本文算法既考虑到自然最近邻用户NaturalNearest-Neighboradpt_r(u)对目标用户的贡献，也融合了活跃用户ActiveNeighbor(u,i)对目标项目的贡献，单独考虑任何一方的集合，都会降低推荐效果造成推荐结果准确度不高的结果。最简约易实现的方法是把自然最近邻用户集合与活跃用户集合的并集作为目标用户u的推荐用户集合RecommendNeighbor(u,i)，即：

3.3　预测评分P̂(u,i)及其准确性

评分预测的准确性与推荐结果的准确性息息相关，选择不同的邻居用户会影响评分预测的结果。获得目标项目u对项目i的推荐邻居集合RecommendNeighbor(u,i)后，按照公式（5）预测目标用户的评分：

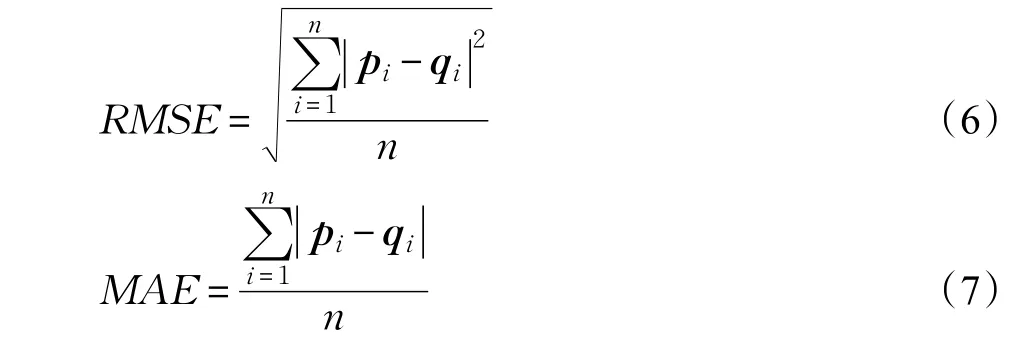
其中，pi向量存放测试集中用户对项目的实际评分，qi存放本文算法预测出的测试集中用户对项目的评分。

4　实验结果分析

4.1　实验数据集

本文仿真实验使用的数据集是明尼苏达大学Group-Lens小组从movielens.umn.edu网站收集的MovieLens 100k Dataset（表2）。MovieLens数据集包含943个用户，1 682部电影，以及用户对电影逾100 000条范围在1～5分之间的整数评分（评分值为0则表示用户未对该电影评分），且每个用户至少对20部以上的电影进行了评分。通过表2对MovieLens数据集中用户数、电影数、评分数、评分范围以及稀疏度的分析可以看出，真实的数据集具有极高的稀疏度。为避免评分填充对邻居选择的影响，应在确定目标用户的推荐邻居集合后对各用户缺失项使用评分均值填充。

表2　MovieLens实验数据集稀疏度

本文算法实验从ml-100k数据集中将随机选出的每个用户对10部电影的实际评分作为ua.test测试集，ml-100k剩余部分作为ua.base训练集，且两部分相互独立。此外，实验还分别在不同用户规模上验证了本文算法在MovieLens数据集上的表现。实验平台为Matlab 2010b版本。

4.2　实验结果分析

首先，本文仿真实验对比了CF-KNN算法和CF3N算法在MovieLens数据集上的RMSE和MAE值，实验结果如图2所示。

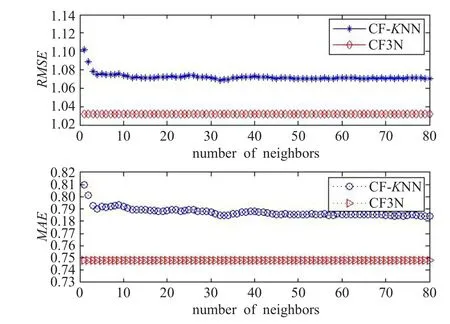
图2　MovieLens上CF-KNN与CF3N算法对比

从图2看出，CF-KNN算法随K值增大，RMSE和MAE值逐渐变小，最后趋于一个常数RMSECF-KNNmin=1.072 9，MAECF-KNNmin=0.788 1。本文算法CF3N，目标用户的邻居个数是算法自适应生成的，通过该算法计算测试集RMSE=1.031 8和MAE=0.748 3。对比发现，CF3N算法在RMSE和MAE两个指标上均优于CF-KNN算法。

其次，本文选择INS-CF[20]算法作为对照，该算法综合考虑用户评分数量和评分质量两方面，提出一种用户有影响力近邻的选择方法，是一种改进的基于用户近邻的推荐方法。本文实验对比了INS-CF算法、CF3N算法在MovieLens数据集上的MAE值，实验结果（如图3）显示，在100～800个邻居规模上，本文算法的MAE值始终小于INS-CF算法的MAE值。

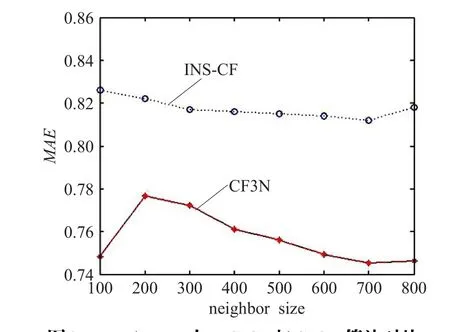
图3　MovieLens上INS-CF与CF3N算法对比

此外，实验还在MovieLens数据集不同用户规模上进行了对比实验。比较CF3N、CF-KNN算法在100～500个用户上的RMSE和MAE值（如图4所示），得出本文算法在推荐准确性上优于CF-KNN算法的结论。

图4　MovieLens不同用户规模上CF-KNN与CF3N对比

5　结束语

本文算法改进了基于K近邻协同过滤算法直接选取K个邻居进行评分预测和推荐时，存在K值对评分预测准确率有影响，算法本身推荐准确率不高，且获取准确率最高的推荐结果实现过程复杂等不足之处。分析传统基于K近邻的协同过滤算法在邻居选择方法存在的不足，提出一种融合用户自然最近邻居的协同过滤推荐算法（CF3N），自适应选取目标用户的自然最近邻用户集合，再融合目标用户的自然最近邻居集与活动近邻用户集，使用融合后得到的邻居集合预测目标用户评分，并在MovieLens数据集上进行对比实验。既避免了选择合适K值较难的问题，也更大程度上提升了推荐结果的准确性和有效性。虽然该推荐算法对解决用户冷启动问题不具备实用性，这也是下一步研究待解决的问题，但实验表明本文算法在邻居选择和推荐结果准确性方面具有一定优越性。

参考文献:

[1]中国互联网络中心（CNNIC）.第38次中国互联网络发展状况统计报告[R].2016.

[2]Wang Hongbing，Shao Shizhi，Zhou Xuan，et al.Preference recommendation for personalized search[J].Knowledge-Based Systems，2016，100：124-136.

[3]Hu Xiao，Zeng An，Shang Mingsheng.Recommendation in evolving online networks[J].The European Physical Journal B，2016，89（2）：1-7.

[4]Bennett P N，Kelly D，White R W，et al.Overview of the special issue on contextual search and recommendation[J].ACMTransactionsonInformationSystems，2015，33（1）：1-7.

[5]Rahul K，Prakash V O.A collaborative recommender system enhanced with particle swarm optimization technique[J].Multimedia Tools Applications，2016，75（15）：9225-9239.

[6]项亮.推荐系统实践[M].北京：人民邮电出版社，2012：61-62，23-34.

[7]Herlocker J L，Konstan J A，Riedl J.Explaining collaborative filtering recommendations[C]//Proceedings of ACM Conference on Computer Supported Cooperative Work，2000：241-250.

[8]Hu Yifan，Koren Y，Volinsky I C.Collaborative filtering for implicit feedback datasets[C]//Proceedings of the 2008 Eighth IEEE International Conference on Data Mining，2008：263-272.

[9]Destosiers C，Karypis G.A comprehensive survey of neighborhood-based recommendation methods[M]//Recommender Systems Handbook.Boston，MA：Springer，2011：107-144.

[10]Li Baoli，Lu Qin，Yu Shiwen.An adaptivek-nearest neighbor text categorization strategy[J].ACM Transactions on Asian Language Information Processing，2004，3（4）：215-226.

[11]罗辛，欧阳元新，熊璋，等.通过相似度支持度优化基于K近邻的协同过滤算法[J].计算机学报，2010，33（8）：1437-1445.

[12]尹航，常桂然，王兴伟.采用聚类算法优化的K近邻协同过滤算法[J].小型微型计算机系统，2013，34（4）：806-809.

[13]黄创光，印鉴，汪静，等.不确定近邻的协同过滤推荐算法[J].计算机学报，2010，33（8）：1369-1377.

[14]Polatidis N，Georgiadis C K.A dynamic multi-level collaborative filtering method for improved recommendations[J].Computer Standards&Interfaces，2017，51：14-21.

[15]Wang Shuhui，Huang Qingming，Jiang Shuqiang，et al.Nearest-neighbor method using multiple neighborhood similarities for social media data mining[J].Neurocomputing，2012，95：105-116.

[16]Zou Xianlin，Zhu Qingsheng.Abnormal structure in regular data revealed by isomap with natural nearest neighbor[C]//Communications in Computer and Information Science.Berlin：Springer-Verlag，2011：538-544.

[17]Zhu Qingsheng，Huang Jinlong，Feng Ji，et al.A clustering algorithm based on natural nearest neighbor[J].Journal of Computational Information Systems，2014，10（13）：5473-5480.

[18]Zhang Shu，Mouhoub M，Sadaoui S.3N-Q：Natural nearest neighbor with quality[J].Computer and Information Science，2014，7（1）：94-102.

[19]Zhu Qingsheng，Zhang Ying，Liu Huijun.Classification algorithm based on natural nearest neighbor[J].Journal of Information and Computational Science，2015，12（2）：573-580.

[20]杨恒宇，李慧宗，林耀进，等.协同过滤中有影响力近邻的选择[J].北京邮电大学学报，2016，39（1）：29-34.