基于高速公路事故预测的主动式巡逻车应急响应研究*
王 璐 朱 宁
(天津大学管理与经济学部 天津 300072)
0 引 言
截至到2016年底,我国的高速公路已发展到13.10万km[1]。随着高速公路建设快速发展,其事故也不断增多,因此,高速公路事故救援成为公路安全研究的重点,其中巡逻车对事故发现和救援起到至关重要的作用。研究表明,受伤人员的生存率随救援时间的增加而逐渐降低,在接到报警的14 min之后,生存率即可降至75%以下[2]。实际工作中,由于高速公路的特殊性,报警人往往不能快速有效地确定自己的位置,降低了救援效率。为了提高高速公路事故救援效率,学者主要针对系统框架、资源分配策略,以及最小化救援时间等问题进行研究。然而,目前已有的巡逻车事件应急响应研究是基于先验的静态历史事故数据或路网结构的,灵活性不足,救援效率在一定程度提升后达到瓶颈。笔者针对以上问题,将高速公路事故预测和巡逻车应急响应结合起来,以达到提高救援效率的目的。
影响高速公路交通事故发生的因素有外因和内因,其中内因为司机本身的状况,例如,年龄、心里因素等,外界因素主要包括交通状况、地理因素和天气因素等。有很多学者对影响交通事故的因素进行分类总结,但是通过影响因素的分类无法对事故进行有效预防和及时救援,因此,自2000年以来,很多学者基于影响交通事故的外因对交通事故的实时预测进行了研究。高速公路事故风险预测的2个数据集主要来源于实时交通流数据和警方数据,它们分别为事故发生前一段时间与交通状态相关的数据集和同一路段的事故数据集。事故的数据主要包括事故发生的时间和地点,交通数据主要包括车辆速度、占有率和流量等。事故预测的指标主要包括提前时间、敏感度和误判率。其中,敏感度表示预测发生事故并且真实发生的事故数占所有真实发生的事故比例,误判率表示将无事故判为有事故占所有实际中无事故的比例。敏感度和误判率往往相互制约,为了便于分析,常常以TPR(ture positive rate)为纵轴,FPR(false positive rate)为横轴,根据模型的不同分类衡量指标绘制成为事故预测ROC曲线图。事故预测主要是通过人工智能或机器学习方法或统计方法对交通状态变量进行筛选,应用筛选出的交通变量训练事故风险预测模型,从而达到对事故风险实时预测的目的。其中机器学习方法主要包括贝叶斯[3-5]和支持向量机[6-7]等,统计方法主要包括logistics等[8-9]。在影响因素方面,一些学者还研究了可见度[10-12]和地理状况[13]与事故之间的实时关系,此外,Tanishita等[14]还考虑了平均速度的变化,研究了平均速度和平均速度的变化对交通事故的影响,应用一个二维累计泊松模型分析日本高速公路平均连续5 min车速监测数据,结果表明,平均速度和平均车速的变化都会影响每公里的交通事故率。
高速公路事件应急管理方面,学者主要研究了系统框架、资源分配策略,以及最小化救援时间等。Zografos等[15]研究了高速公路交通流恢复的最小化集成方法框架。该模型由3个基本模块构成:①通过服务区域的数量决定交通流恢复需要车的数量;②估计总事故清除时间;③根据高速公路的总事故清除时间、高速公路几何特性和交通特性对延误时间进行了估计。研究表明该模型可以用来确定系统需要车的数量,制定调度策略。Lou Yingyan等[16]研究了在确定性和随机性2种情况下检测、响应和清除交通事件的巡逻服务部署问题,这2个情况的主要目标是尽量减少总的事件响应时间。Wu Weitiao等[17]开发了一个基于离散事件的仿真模型来模拟巡逻过程,来分析新的调度方法的有效性,研究表明将会减少9.2%的事故清除时间。然而,这些研究基于设定的场景,在应急响应上有很大的局限性,笔者应用最邻近(KNN)方法对美国高速公路I-5s高速公路的一段路程进行事故预测,用python搭载仿真路网,以实时预测的数据作为仿真参数输入,从主动救援的角度减少事故响应时间。
1 问题描述
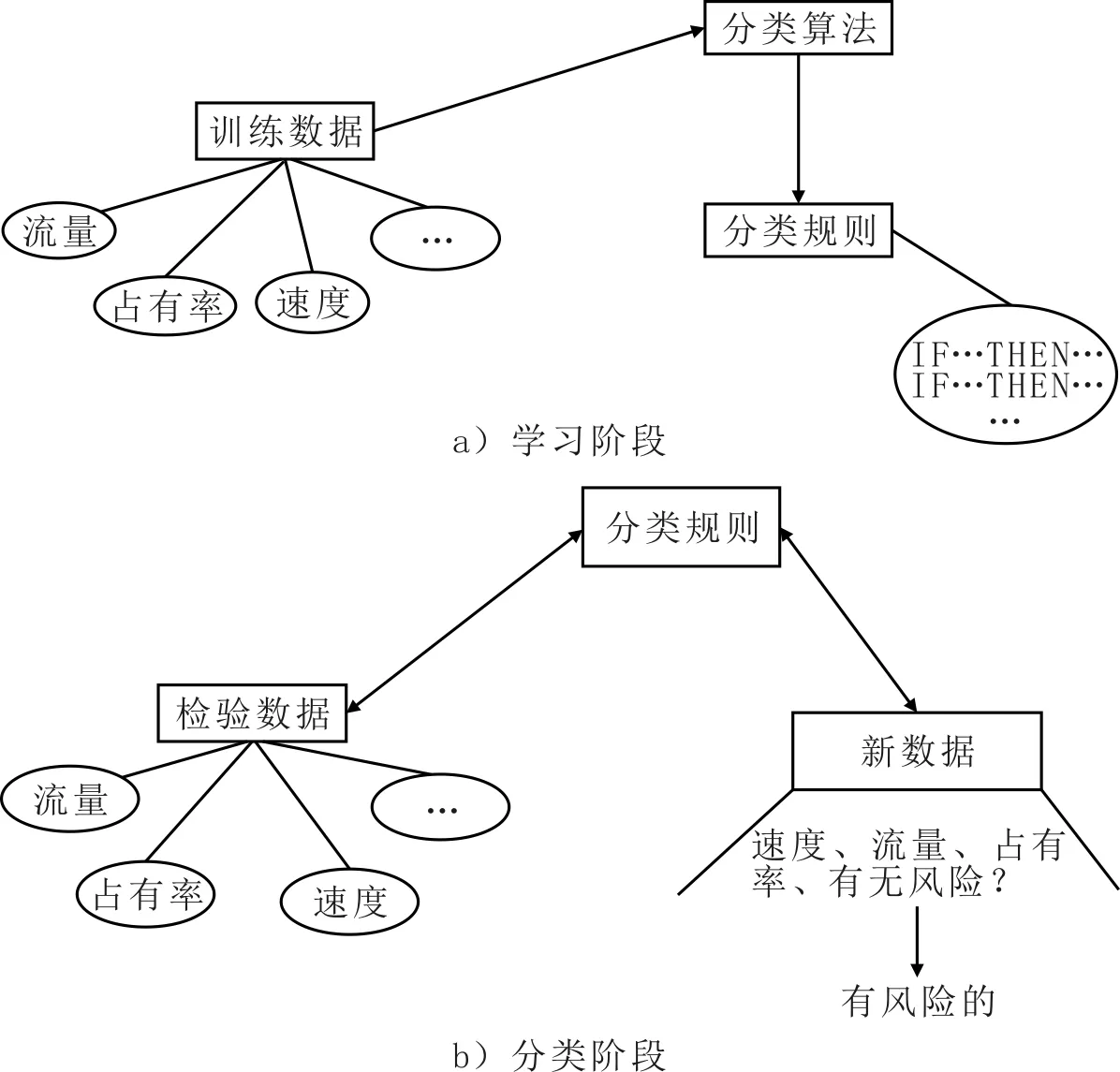
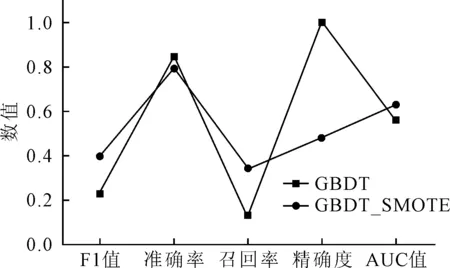
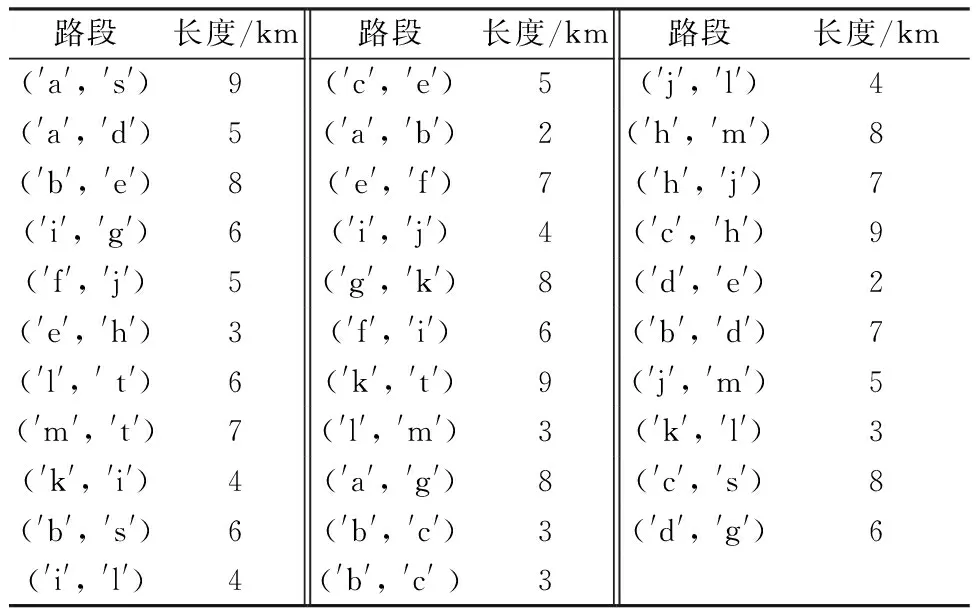
基于高速公路是事故实时预测的主动应急救援问题可以描述如下:用无向图G=(V,E)表示研究区域的交通网络,顶点为V={v0,v1,v2,…,vn},边缘为E={(vi,vj):vi,vj∈V,i 图1 高速公路网络结构Fig.1 Highway network 事故预测问题的本质是数据分类问题,包括学习阶段和分类阶段。学习阶段如图2 a)所示,用分类算法训练交通状态数据,如流量、占有率、速度等。学习的模型和分类器以分类规则的形式给出,构建事故预测模型。分类阶段如图2 b)所示,检验数据用于评估分类规则的准确率,如果准确率较高,可以用这些规则对新的交通状态数据进行判断,预测事故是否发生。 图2 交通状态数据分类过程Fig.2 Classification of traffic 事故预测主要包括7个部分:确定目标、数据收集、数据处理、变量筛选、训练预测模型、预测事故,以及预测结果分析。事故预测的目标主要是尽可能准确的预测事故是否发生。收集到数据后,要进行特征向量构建,归一化,均衡数据处理,并对特征向量进行特征筛选,找出相关度比较大的交通状态特征。 2.2.1基于过采样的SMOTE算法 由于常见的随机过采样采取简单复制事件集数据样本的策略来增加少数类样本,这样容易产生模型过拟合的问题,人们对其进行了改进。SMOTE[18](synthetic minority oversampling techniques)是一种效果较好的合成采样技术,它的基本思想是对少数类样本进行分析,并根据少数类样本人工合成新样本添加到原始的数据集中,合成少数类样本示意图见图3。通过SMOTE算法,事故和非事故数据集可以达到平衡。 图3 合成少数类样本示意图Fig.3 The diagram of synthetic the minority sample SMOTE算法具体步骤如下。 1)对于事件类中每一个样本αi,以欧氏距离为标准计算它到事件类样本集Sacc中所有样本的距离,得到其k近邻。 2)根据事件与非是故不平衡比例设置一个采样比例以确定采样倍率N,对于每一个事件类样本αi,从其k近邻中随机选择若干个样本,假设选择的近邻为 。 3)对于每一个随机选出的近邻e,分别与原样本按照如下的公式构建新的样本。 2.2.2基于Relief的特征变量筛选 Relief[19]算法最早由Kira提出,是一种特征权重算法,根据各个特征和类别的相关性赋予特征不同的权重,权重小于某个阈值的特征将被移除。Relief算法中特征和类别的相关性是基于特征对近距离样本的区分能力,伪代码见表1。 表1 Relief算法步骤Tab.1 The procedures of Relief method 2.2.3GBDT分类器 GBDT[20]是一种迭代的决策树算法,该算法由多棵决策树组成,所有树的结论累加起来做最终答案。它在被提出之初就和SVM一起被认为是泛化能力较强的算法。其适用性较为广泛,分类效果好,已经在各个领域得到广泛的应用。 其步骤如下。 1)初始化,估计使损失函数极小化的常数值,它是只有1个根节点的树,即γ是一个常数值。 2)(a)计算损失函数的负梯度在当前模型的值,将它作为残差的估计。 (b)估计叶节点区域,以拟合残差的近似值。 (c)利用线性搜索估计叶节点区域的值,使损失函数极小化。 3)得到更新的模型为 选取加利福尼亚I-5s高速公路上34 km长的路段为研究路段,该路段起于San Diego 86 km,止于Orange 120 km。 所使用的数据主要包括2个数据集:①加利福尼亚交通局测量系统采集的交通状态数据集;②加利福尼亚交通管理部门统计整理的交通事件数据集。下面分别对2个数据集进行详细介绍。交通状态数据来自该路段上的13个检测器,包括2013年1月1日-2014年1月1日间1年的数据。这些检测器每30 s检测1次交通数据并实时传回控制中心,这些交通数据主要包括交通流量,占有率和车速。为了防止数据的偶然性,将每个检测器在5 min的时间段的数据作为研究对象的最小单位,为了避免事件时间不准确带来的误差,提取交通事件时间之前在5~10 min的交通状态变量。例如,如果一个事件发生在20:56,相应的交通数据是交通情况从20:46-20:51。所选数据集中,数据完整并且可以进行研究的共计138起。对于事件数据集中的每个事件,选取事件发生前至少1 h之前或至少1 h之后没发生事件的案例作为对照组。应用收集的数据构建17个交通特征变量。 经过特征向量构建,SMOTE平衡数据集,Relief特征变量筛选后,应用GBDT分类器进行分类预测,得到GBDT模型对平横数据和不平衡数据的预测结果对比,见图4。 图4 基于GBDT分类器的平衡与不平衡数据集对比Fig.4 Comparation of balanced and unbalanced datasets under GBDT 从图中可以看出相比不平衡数据,平衡数据下GBDT在f1_score和auc方面有一定提高,相比不平衡数据,平衡数据下GBDT的accuracy指标略低,差值为0.02左右,说明整体预测能力略弱一些。 为了使研究问题简化清晰,在结合巡逻车系统的实际情况下,对巡逻车系统模型进行如下假设。 1) 事故发生的间隔时间、地点是随机的,并且是相互独立的。 2) 对于不同的事故,巡逻队的处理时间是不确定的,事件处理时间为1个随机变量。 3) 预测的事故路段的排队方式为损失制(正常的排队是指虽然没有车,但是可以把事故信息存储下来,有空闲车辆时再处理巡逻事故信息。损失制是指在没有空闲车的情况下,不对事故信息进行存储)。 4) 预测的事故路段的应急响应方式是优先权服务,即事故报警请求援助的情况下优先级最高。 5) 路网的路阻已知且不随时间变化,即路网是一个静态系统。 巡逻车响应系统是1个离散事件系统[21],基于事故风险预测的巡逻系统的实体主要包括风险路段、巡逻车、路网路段和事故报警路段,各实体的属性、活动及状态见表2。 巡逻车响应的事故包括2种,即事故风险路段和事故报警路段。其中预测的风险路段又包括将会真实发生的或误判的。定义巡逻车响应事故报警时的状态是一级繁忙状态,巡逻车响应事故预警时的状态是二级繁忙状态。模型的事件主要包括事故预测事件、事故报警事件、巡逻车到达事件和巡逻车离开事件等几种,分别介绍如下。 表2 系统要素属性,活动与状态Tab.2 System element properties, activities and status 1) 事故预测事件与事故报警事件。根据假设的事故预测分布情况,产生事故预测事件。当发生事故预测事件时,首先判断巡逻车的状态,如果巡逻车处于“忙”状态,则巡逻车保持当前状态,此时不再响应事故预测事件或报警事件,按照最短路径向事故预测路段行驶。 2) 巡逻车到达事件与离开事件。巡逻车到达目的路段后,路段的状态由“等待巡逻”变为“接受巡逻”。巡逻车离开目的路段后,路段的状态由“接受响应”变为“闲”状态。 巡逻车仿真系统参数主要分为3大类,分别为路网参数、巡逻车仿真参数和事故预测参数。计算机仿真所采用的高速公路网络结构如图1所示,路网中有15个节点、32条边,具体路段数据见表3。 巡逻车仿真参数包括巡逻车的数量、速度和常规巡逻路径。设置1辆巡逻车,其速度为60 km/h,常规巡逻路径为g-i-k-g。事故提前预测时间为5 min,频率为5 min/次。 表3 计算机仿真高速公路路段Tab.3 Freeway road segment for computer simulation 事故预测仿真参数主要包括提前预测时间、敏感度和误判率、事故预测的频率、事故发生的时间和事故的处理时间。事故的发生地点是随机的,事故的处理时间为0~20 min的随机分布。事故的提前预测时间为5 min,根据GBDT算法,在高速公路美国加利福尼亚I-5s数据下得到交通事故预测数据如图3所示,将图3中的数据作为事故预测敏感度和误判率。表4为California州I-5s高速公路平均每100 km非工作日事件发生时间分布,其中事件均值在0.11~1.30,最小值在各个不同时刻均为0,事件高峰在6:00,15:00和17:00左右达到。将表4作为交通事件频率仿真参数。 表4 California I-5 s平均每100 km非工作日事故发生时间分布Tab.4 California I-5 s average 100 km weekend accident occurrence time distribution 事故平均响应时间用UBRT表示,平均无响应事件数目用NR表示。从表5可以看出,随着TPR的增加,FPR也逐渐增加,事故平均响应时间变小,与此同时,无响应事故也逐渐增多,在工作日最低响应时间分别为17.2 min,节省了约6 min。但与此同时,无响应的事故数也增多,需要合理配置巡逻车辆。 表5 平均应急响应时间仿真结果Tab.5 Result of the average emergency response 1) 以往的研究基于先验历史事故数据或路网结构,其本质是静态的且灵活性不足。针对这一问题,基于采集的高速公路事故数据和交通状态数据,对巡逻车主动式应急响应时间进行了研究。模型的有效性得到验证。 2) 研究只考虑了1个巡逻车基于事故预测的事故应急响应,没有研究多个巡逻车时,巡逻车该如何配置以及事故预测模型如何选择。为了更加全面的研究基于事故预测的事故响应对救援时间的影响,下一步的研究将基于巡逻队整体巡逻效率而展开。仿真具有随机性,仿真实验展现的是一定交通情况下模型的有效性,需要对可靠性进行验证。 参考文献References [1]国家统计局.中国统计年鉴[Z].北京:中国统计出版社,2016. National Bureau of Statistics. China Statistical Yearbook[Z]. Beijing: China Statistics Press, 2016. (in Chinese) [2]杨惠敏,陈雨人,方守恩,等.高速公路交通事故救援时间与生存率关系模型研究[J].交通信息与安全,2015,33(4):82-86. YANG Huimin, CHEN Yuren, FANG Shou′en, et al. Study on the Model of Relationship between Highway Traffic Accident Rescue Time and Survival Rate[J]. Journal of Transport Information and Safety, 2015,33(4):82-86.(in Chinese) [3]DEUBLEIN M, SCHUBERT M, ADEY B T, et al. Prediction of road accidents: A Bayesian hierarchical approach[J]. Accident Analysis & Prevention, 2013,51(4):274-291. [4]HOSSAIN M, MUROMACHI Y. A Bayesian network based framework for real-time crash prediction on the basic freeway segments of urban expressways[J]. Accident Analysis & Prevention, 2012,45(1):373. [5]SUN J, SUN J. A dynamic Bayesian network model for real-time crash prediction using traffic speed conditions data[J]. Transportation Research Part C: Emerging Technologies, 2015(54):176-186. [6]QU X, WANG W, WANG W, et al. Real-time freeway sideswipe crash prediction by support vector machine[J]. Intelligent Transport Systems Iet, 2013,7(4):445-453. [7]YU R, ABDELATY M. Utilizing support vector machine in real-time crash risk evaluation[J]. Accident Analysis & Prevention, 2013,51(2):252-259. [8]ANASTASOPOULOS P C, MANNERING F L. An empirical assessment of fixed and random parameter Logit models using crash- and non-crash-specific injury data[J]. Accident Analysis & Prevention, 2011,43(3):1140-1147. [9]LEE J, YASMIN S, ELURU N, et al. Analysis of crash proportion by vehicle type at traffic analysis zone level: A mixed fractional split multinomial Logit modeling approach with spatial effects[J]. Accident Analysis and Prevention, 2018,111:12-22. [10]ABDEL-ATY M A, HASSAN H M, AHMED M, et al. Real-time prediction of visibility related crashes[J]. Transportation Research Part C: Emerging Technologies, 2012,24(9):288-298. [11] ABDEL-ATY M A. Predicting reduced visibility related crashes on freeways using real-time traffic flow data[J]. Journal of Safety Research, 2013,45:29-36. [12]ABDEL-ATY M A, HASSAN H M, AHMED M. Real-time analysis of visibility related crashes: can loop detector and AVI data predict them equally?[C]. Transportation Research Board 91st Annual Meeting. Wangshington,D.C: TRB, 2012. [13]WANG L, ABDEL-ATY M, LEE J, SHI Q. Analysis of real-time crash risk for expressway ramps using traffic, geometric, trip generation, and socio-demographic predictors[J/OL].(2017-7)[2018-3-16] https://doi.org/10.1016/j.aap.2017.06.003. [14]TANISHITA M, VAN WEE B. Impact of vehicle speeds and changes in mean speeds on per vehicle-kilometer traffic accident rates in Japan[J]. IATSS Research, 2017,41(3):107-112. [15]ZOGRAFOS K G, NATHANAIL T, MICHALOPOULOS P. Analytical framework for minimizing freeway-incident response time[J]. Journal of Transportation Engineering, 1993,119(4):535-549. [16]LOU Y, YIN Y, LAWPHONGPANICH S. Freeway service patrol deployment planning for incident management and congestion mitigation[J]. Transportation Research Part C: Emerging Technologies, 2011,19(2):283-295. [17]CHEN H, CHENG T, WISE S. Developing an online cooperative police patrol routing strategy[J/OL].(2017-3)[2018-3-6] https://doi.org/10.1016/j.compenvurbsys.2016.10.013. [18]CHAWLA N V, BOWYER K W, HALL L O, et al. SMOTE: synthetic minority over-sampling technique[J]. Journal of Artificial Intelligence Research, 2002,16(1):321-357. [19]KONONENKO I. Estimating attributes: analysis and extensions of RELIEF[C]. European Conference on Machine Learning, Catania, Italy: ECML-PKDD, 1994. [20]FRIEDMAN J H. Greedy function approximation: A gradient boosting machine[J]. Annals of Statistics, 2001,29(5):1189-1232. [21]CASSANDRAS C G, LAFORTUNE S. Introduction to Discrete Event Systems[M]. Boston: Springer US, 2008.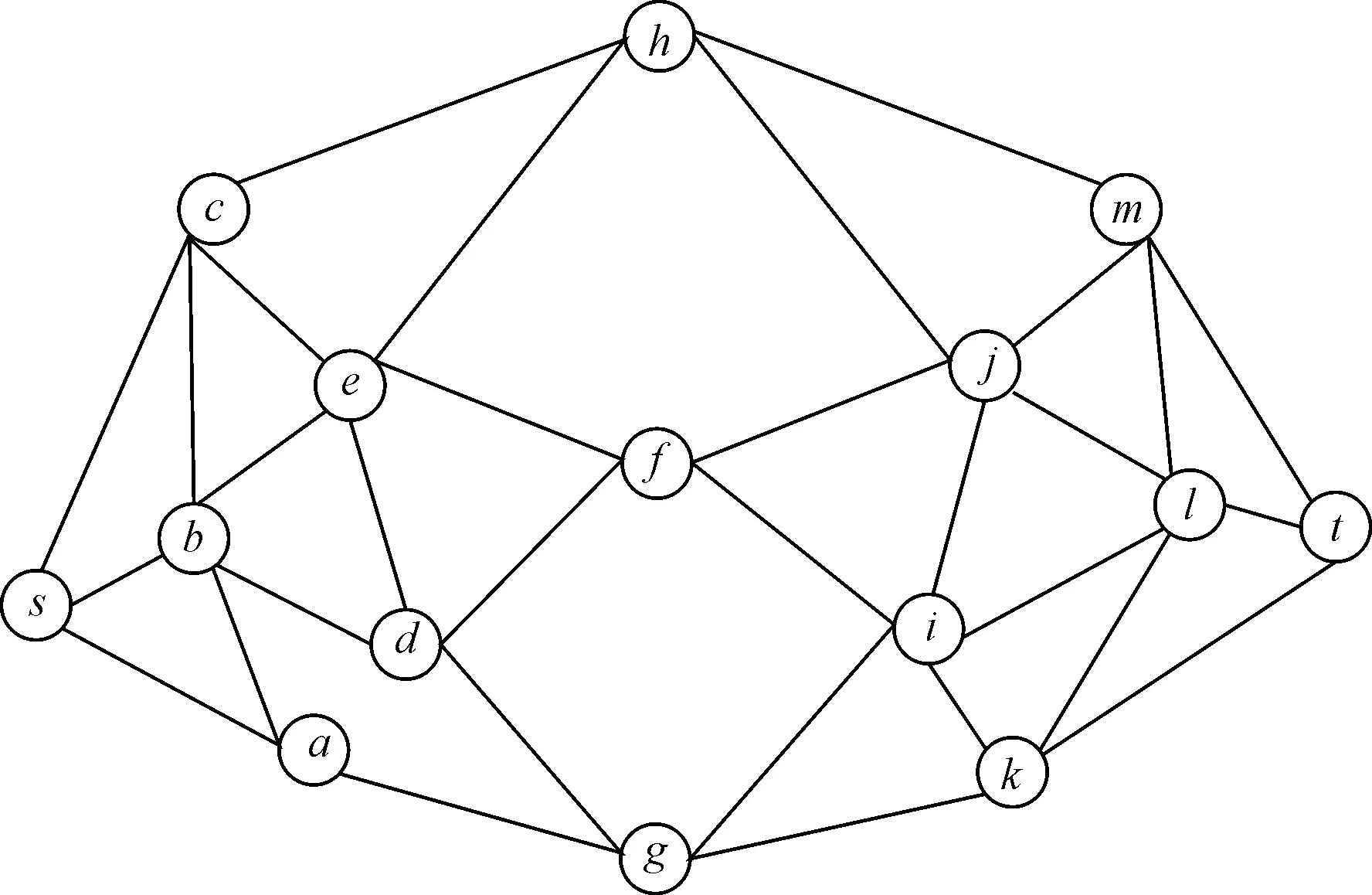
2 事故预测模型
2.1 事故预测流程
2.2 基于SMOTE,Relief和GBDT的交通事故预测方法


2.3 事故预测结果
3 巡逻车应急响应仿真模型
3.1 模型假设
3.2 系统要素分析

4 仿真实验
4.1 仿真实验参数设置

4.2 结果统计与分析

5 结 论

