基于多级网络的多模式交通配流研究*

于晓桦　晏克非　牟振华　张　辉

(1.山东建筑大学交通工程学院　济南 250101；2.同济大学交通运输工程学院　上海 201804;3.北京工业大学城市交通学院　北京 100124)

0　引　言

流量分配是交通需求预测中的重要内容。随着交通网络结构的变化和出行模式的多样化，城市多模式复合交通网络构建已初具规模。在城市复合交通网络形式下，不同的出行方式、换乘点和出行路径，带给出行者的效用均不相同，且各种方式选择之间的相互影响，给多模式复合交通需求预测带来诸多的不确定性。而目前常用的传统“四阶段”法分配模型，是先将“人次”转化为“车次”，再将车次在单一的道路网络上进行分配[1]。4个阶段相互隔离，不适用于目前多模式复合网络的交通分配，因此，亟须一种可以将“人次”直接分配在多模式网络上的分配方法。

目前，已有一些学者研究多模式网络的分配问题。比较认可的方法有基于四阶段法的“组合模型”。Pallottino[2],Lozano and Storchi[3]分别提出基于超级路径的多模式交通网络模型，他们将超级网络的“路段”分为2种:①真实的路段或轨道线段；②描述换乘行为的换乘段。出行者在这种网络中寻找出行阻抗最小的“超级路径”走行，从而得到带有换乘的组合交通的网络分配。Fernandez等[4]提出多种方法来解决组合出行中换乘点选择的问题，他们将Nest-Logit模型嵌入到超级网络中，解决不同换乘点路径与不同方式选择的不同等性问题。Cipriani等[5]研究了多模式网络的优化问题，但没有考虑不同模式间的相互干扰。Lo H.K.等[6]提出一种状态扩展网络模型(state-augmented multi-modal,SAM)，描述多模式出行中的换乘选择问题。王炜等[7]提出基于双层模型的机动车道、自行车道、人行道的整体设计模型。邵春福等[8]分析弹性需求下组合出行模式的交通平衡条件，提出与平衡条件等价的变分不等式模型。贾洪飞等[9]基于心理学和行为科学，提出出行方式选择阶段的划分模型。然而，在现有研究中，多模式复合交通配流中2个关键问题仍然没有有效的解决:①组合出行中的换乘点选择问题；②多模式交通方式选择逻辑问题。因此，笔者提出具有合理逻辑结构的多级网络模型，解决带有组合出行的多模式交通配流问题，为复合网络客流预测提供参考。

1　复合交通网络结构描述

1.1　物理结构描述

一般来说，网络是由路段与节点组成，记作G=(E,V)。E=(e1,e2,…,en)为节点集合；V=(v1,v2,…,vn)为路段集合。连接网络中任意一组有向线段系列称为一条路径，所有路径的集合组成网络[10]。

多模式复合交通网络从物理形态上看，由道路网络、轨道网络通过换乘枢纽的锚固作用复合成的多层立体网络，因此可记作G=(E1,E2,V1,V2)。E1为道路节点集合(例如交叉口)；E2为客流换乘节点集合(例如轨道车站)；V1为轨道线段集合；V2为道路路段集合。其中，换乘节点是道路网络与轨道网络的互通节点，出行者在换乘节点处可实现道路方式与轨道方式的相互转换。

道路网络又包括小汽车网络和公交车网络，虽然小汽车与公交车交通方式共用道路网络资源，但公交车有自己固定行驶线路，因此，公交车网络可以描述为固定在道路网络之上的虚拟网络，即“超级网络”[11]。以小汽车、公交、轨道3个模式子网描述多模式复合交通网络，表示为G=(E1,E2,V1,V2,V3)。E1为道路节点集合；E2为客流换乘节点集合；V1为轨道线段集合；V2为公交线段集合；V3为小汽车路段集合[12-14]。

复合交通网络中的出行路径用图1说明，图中复合交通网络包含小汽车、轨道和公交等3个单模式子网及A,B,C,D4个换乘点，假设某出行者从起始点A到终止点D有小汽车、小汽车-轨道、公交、公交-轨道4种出行方式和多条出行路径：出行者可以从A点驾车直接到D点；或驾车到换乘点B停车换乘轨道交通到D点；或乘坐公交直接到D点；或乘坐公交车到B或C点换乘轨道交通到D点。组合方式出行要涉及到一个以上的模式子网，涉及到多模式之间的换乘，涉及到方式选择、路径选择和换乘点的选择，从而成为网络分析中的难点问题。

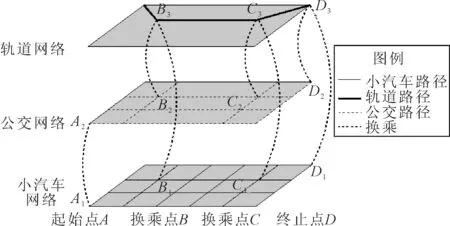
图1　多模式复合交通网络物理结构Fig.1　Physical structure of multimodal composite transportation network

1.2　逻辑结构描述

就出行结构而言，复合交通网络由多模式方式出行路径构成，多模式出行路径是由出行方式段和节点换乘段组成，因此，复合网络可以转化为用不同线段连接的平面拓展网络。平面拓展网络是将起讫点间所有可能的出行方式、换乘方式和换乘点穷举表示，从而将网络中任意点间所有可能的出行方式链全部表示出来。但其并不涉及道路路径的选择。例如，图1的多模式复合交通网络表示为平面拓展网络形式如图2。

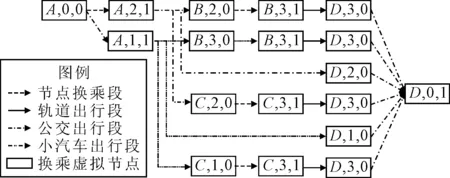
图2　平面拓展网络结构Fig.2　state-augmented structure

图2中，节点方框中的数据依次代表节点编号、方式编号和到达/出发编号。其中，节点编号对应图1中的A,B,C,D4个节点，拓展网络中的2个虚拟节点对应实际网络中一个真实换乘点，以到达/出发编号区分。方式编号代表不同的出行方式，0表示步行，1为小汽车，2为公交车，3为轨道交通。图中的6条路径代表着6种出行方式链，分别为：小汽车直达、公交直达、小汽车-轨道(B点换乘)、小汽车-轨道(C点换乘)、公交车-轨道(B点换乘)、公交车-轨道(C点换乘)。因此，平面拓展网络中的每一条线径确定了一种交通出行方式和换乘点，但没有确定道路路径的选择，换句话说，涉及到小汽车出行方式的线段实际上包括了多条小汽车出行路径。

拓展网络为多模式交通分配提供了网络平台，按照拓展路径阻抗将全方式交通需求分配到拓展网络中，得到不同方式、不同换乘点的出行量。然而，在拓展网络中，不同的换乘点、出行方式都对应各自的线段，这样在分配中会导致类似“红-蓝巴士悖论”那样的IIA问题[15]。为了避免这种问题，将平面拓展网络流量分配时的逻辑关系用巢式模型进行分析，称为多级网络分析方法。

2　基于多级网络的流量分配模型

2.1　多级网络流量分配模型

多级网络是基于网络的逻辑结构，将多模式复合网络按照出行方式选择、换乘点选择和道路路径选择等逻辑关系，拓展为多级巢式网络结构。例如3级网络结构，最下层为小汽车通行的道路网络，中间层为在换乘点展开的平面拓展网络，最上层为各种单一方式和组合方式组成的出行方式网络。多级网络的交通需求预测方法是对多级“路径”进行枚举分析与随机概率分配的过程，步骤如下。

步骤1。计算实际网络中各种单一模式路段与多模式换乘节点阻抗。

步骤2。计算多级网络的流量分配概率并设置各级网络选择的约束条件。

步骤3。按照概率模型将总出行量分配在各级网络的各条路段(线段)上。

因此，基于多级网络的交通需求预测模型可以构建为Nest-Logit模型形式，将多模式复合交通网络的出行描述为“以何种方式、在哪个换乘点、选择哪条实际路径”的出行概率，并表达为条件概率形式为

(1)

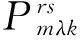
2.2　多级网络路径(线路)阻抗分析

2.2.1小汽车路径阻抗

在多级网络模型中，模型的下层阻抗决定模型上层阻抗，因此，从模型最下层计算路径阻抗。

以3级网络为例，模型的最下层为小汽车出行路径阻抗。小汽车出行时间是道路流量的函数，小汽车路段的出行时间用BPR函数表示为

(2)

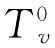
则小汽车出行路径k对应的出行时间为

(3)

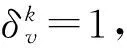
(4)

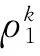
2.2.2轨道交通线路阻抗

多级网络的第二层是以人次进行的路径选择，涉及到轨道、常规公交及换乘点的路径阻抗,因此，要以人次为单位进行线路阻抗的计算。

轨道交通的发车间隔与行车路线都是固定的，轨道网络中两点之间的出行时间是确定的，因此轨道线路阻抗不涉及到路径的选择、不涉及到车辆运行的阻抗[16]。轨道交通的线路阻抗是人们的感知时间、轨道交通费用与换乘次数的函数，表示为

(5)

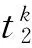
轨道交通线路的感知出行时间是轨道线段感知出行时间的和。

(6)

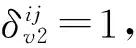
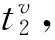
(7)

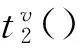
2.2.3公交车路径阻抗

与轨道交通相似，公交车的发车间隔与行车路线也都是事先设定的，因此，公交车路径阻抗表示为

(8)

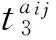
公交车乘客的路径出行时间为

(9)

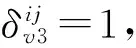
值得注意的是，公交车行驶时间既受到道路流量的影响，也受到车厢客流量的影响[17]。换句话说，道路流量过大，或者车内过于拥挤，都会使公交阻抗增加，影响出行者选择公交车出行方式。因此，采用2次BPR函数计算公交乘客的路径出行时间。

第一次，考虑道路流量影响计算公交车实际运行时间。

(10)

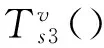
第二次，采用乘坐不舒适性函数计算公交路段阻抗，表示为

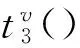
2.2.4换乘节点阻抗

换乘节点阻抗是指不同方式间的换乘阻抗，由换乘时间和常数项构成[18]，表示为

(12)

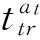
(13)

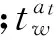
2.3　流量分配模型约束条件

由于实际中多模式复合交通网络中OD对与换乘节点众多，将其扩展为多级网络存在很大困难。如果根据实际情况对各级网络构造与模型建立添加合理的约束条件，将有利于模型的转化与求解，并更加符合实际情况。多级网络中，模型下级的选择阻抗决定模型上一级的选择，因此，应从模型第三级开始，解释模型构造及其约束条件。

1) 模型第三级——道路路径选择。道路路径选择概率是在出行方式和换乘点既定下的条件概率。出行方式和换乘点既定，意味着平面拓展网络路径既定。道路路径选择只涉及到实际交通网络中小汽车出行路径的选择，因此将平面拓展网络的小汽车段与实际网络中小汽车出行路径相对应，见图3。

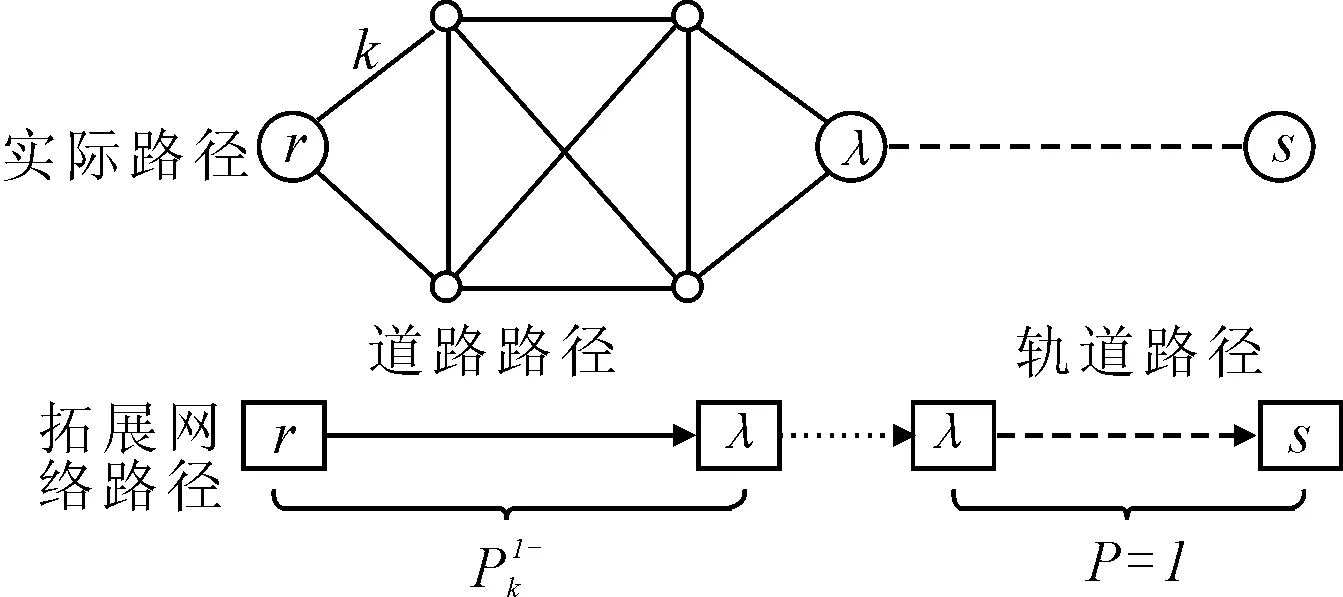
图3　实际路径与拓展网络路径对照图Fig.3　Path comparison of real network and augmented network

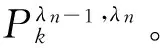
(14)

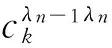
则路径选择条件概率为拓展网络中各段路径选择概率的乘积，表示为

(15)

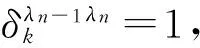
交通网络中，2点间存在若干条路径，然而由于环状网络的存在，理论上路径的条数是无数条，按照阻抗概率，这些路径都会参与分配交通量。然而在实际走行时，出行者不会选择过于迂回的路径的走行。因此，有必要对换乘点间实际网络中的有效路径进行筛选，作为参与分配的路径选择约束条件。

若路径k为换乘点λn-1,λn间的有效路径，则应满足：①路径k非环状路径；②路径k阻抗在λn-1,λn间最短路径的(1+H)倍之内，即

(16)

式中：H为非负常数，称为有效路径系数。该系数与路网结构、路径长度和交通流量有关，但可根据实际调查估计其合理取值。

2) 模型第二级——换乘节点选择。换乘点选择概率是在交通方式既定下，对换乘点选择的条件概率，换乘点的选择只涉及到组合交通方式。出行方式确定条件下，一种换乘方案对应着平面拓展网络中的唯一路径，因此可认为换乘点的选择概率是拓展网络中各条路径的选择概率。拓展网络路径是由方式段与换乘段组成，对于公共交通方式，由于路径是固定的，2个换乘点间路径阻抗是确定的，由式(5)和(8)确定；对于小汽车方式，2点间有多条出行路径，路径阻抗表示为多条实际道路路径阻抗的合成效用(logsum)形式

(17)

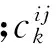
平面拓展网络中出行路径(包括组合出行方式)阻抗函数表示为

(18)

其中，若在由(λ,b)确定的拓展网络路径上，则δ(p,a)=1，否则为0。

则换乘点选择的条件概率为

(19)

虽然起讫点间可能存在诸多换乘点，但并非每个换乘点都有被选择的可能，这不仅取决于换乘点的个数限制，还取决于接驳方式时间的限制和换乘可能性。根据我国大中城市居民出行情况，对于有效换乘点的选择有以下3个约束。

1) 换乘点个数约束。拓展网络路径中的换乘个数最多不超过2个(不包括起讫点的步行与交通方式的衔接)。

2) 接驳方式时间约束。换乘点应在距起点或终点的一定接驳时间(如10 min)以内，并根据不同方式确定合理接驳距离。选择组合出行方式的出行者，大多是以轨道交通为主体出行方式的，若接驳轨道交通的时间过长，出行者一般不会“长途跋涉”地选择轨道交通出行了。因此，应根据调查首先确定接驳时间或距离，再以此对出行路径上的换乘点进行筛选，有利于拓展网络构造的简化。图4 a)为r到s的实际路径，将其中小汽车-轨道出行方式转为拓展网络路径如图4 b)所示，由于接驳距离的约束，可将从换乘点A3和A4的出行路径删除，将r到s小汽车-轨道有效路径简化为图4 c)。

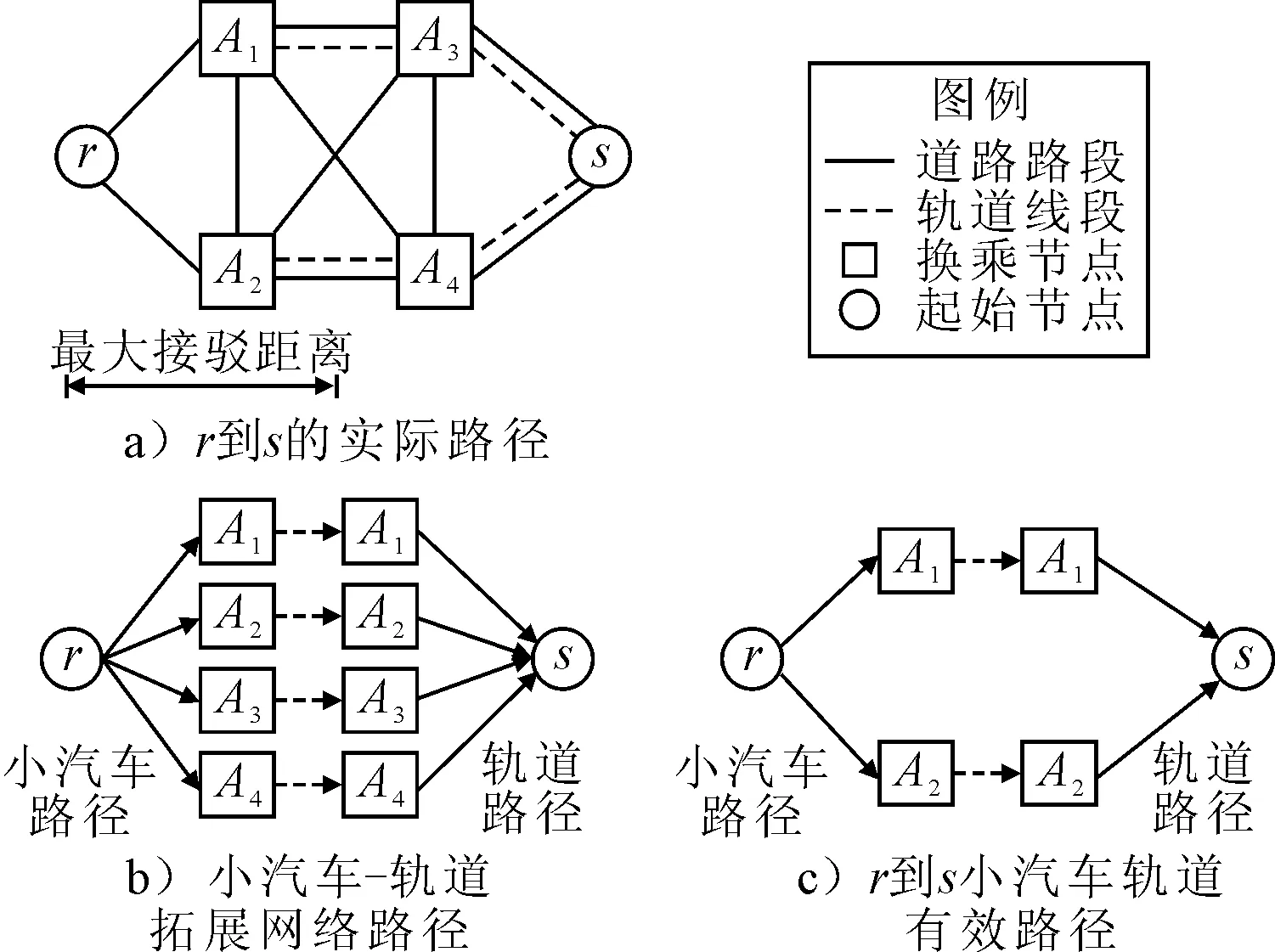
图4　换乘点的筛选示意图Fig.4　selection of transfer nodes

3) 模型第一级——出行方式选择。出行方式选择将拓展网络简化为由各种出行方式组成的网络，并且不存在换乘点的差异。实际上，出行方式选择实际上也是Nest-Logit形式，单一交通方式与轨道交通接驳的组合交通方式应属于不同的“巢”。

出行方式选择是将起讫点间每一种交通方式看作一个选择肢，单一出行方式与典型组合出行方式为并列选择肢，组合出行方式再划分为轨道与其他接驳方式的组合。典型组合出行的子路径以合成效用(logsum)表示。

应用N-L模型，出行方式选择概率为

Pm=Pm1m2=Pm2/m1Pm1=

(20)

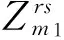
出行方式网络的各条路径可能存在若干个换乘点方案，则将同类组合出行方式不同换乘点方案的阻抗表示为

(21)

所有组合出行方式的阻抗(合成效用)为：

(22)

由此，3级网络分析模型构造完成，并在可能的出行约束下，模型的构建与求解均可以得到一定简化。

3　模型求解

多级网络的流量分配问题描述为随机用户均衡问题(SUE)，即在平衡点，某个OD对间所有被利用的路径上，并不一定有相同的测定阻抗值，而是与出行者的感知阻抗有关，所以被利用的路径上的流量为

(23)

若各条路径阻抗是固定的，则多模式复合交通网络中各条路径被选择的概率可由式(1)直接求出，路径流量也可直接得到。然而阻抗不仅是随机变量，而且与流量是相关的，因此通过算法进行反复迭代，网络流量才能达到平衡状态。求解SUE问题的最常用的算法是连续平均法(MSA)，对于具有N-L结构的多级网络流量分配问题涉及到多级网络中的流量均衡，其算法步骤如下。

步骤1。网络转换。结合有效路径、节点约束条件，将实际网络转化为多级网络：将小汽车出行网络作为3级网络、平面拓展网络作为2级网络、出行方式网络作为一级网络。

步骤3。更新阻抗。首先根据式(4)更新第3级网络的小汽车路段阻抗；再根据式(5)(8)(14)、(18)更新第二级网络(拓展网络)各路径阻抗；最后根据式(21)、(22)更新上级网络(出行方式网络)的各段阻抗。

步骤5。更新网络各段流量。

(24)

步骤6。判断是否满足收敛条件。如果满足则终止循环，否则返回第2步，n=n+1。收敛条件可定义为

(25)

式中：κ为预先指定的常数。

4　算例分析

设想一种情景来验证多级网络交通配流问题，如图5所示。该网络包括：4个节点，其中A为起始点，D为终止点，B和C为换乘点；小汽车道路网络，包括AC,CD,AB,BD,AD5条路段；公交网络，包括AB,BD2条公交线段；轨道网络，包括BD,CD2条轨道线段。从A到D的固定需求为300人次/h。复合网络的相关特性参数见表1，表2；出行阻抗参数见表3。

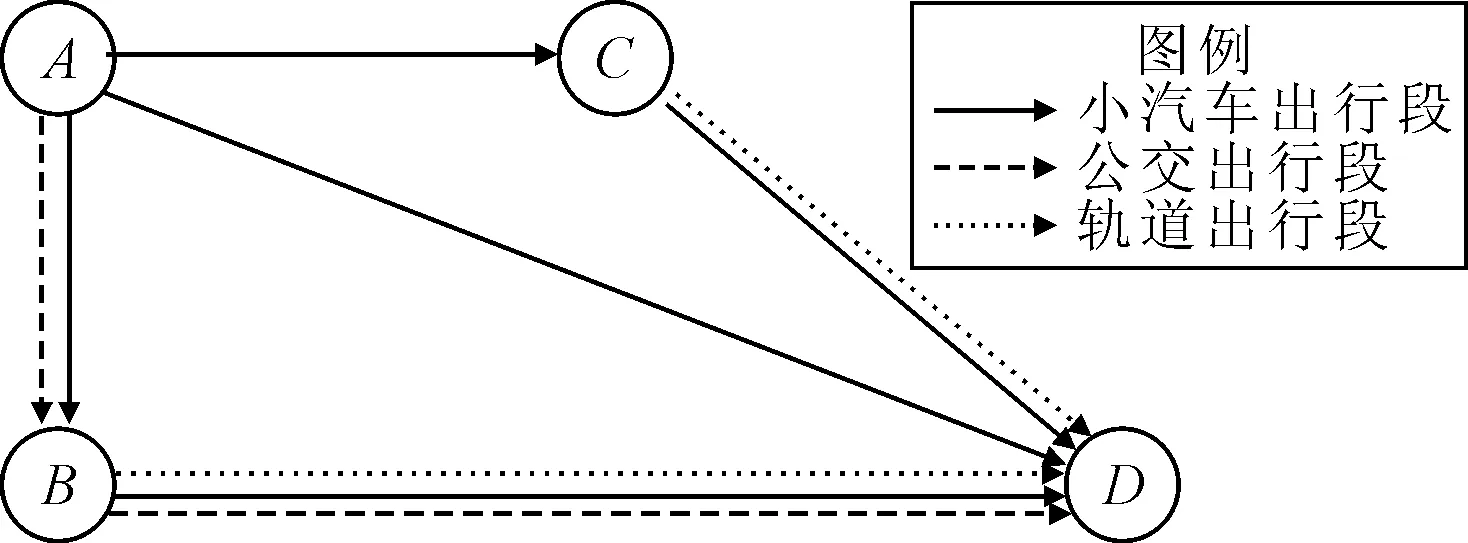
图5　复合交通网络算例Fig.5　Example of composite network

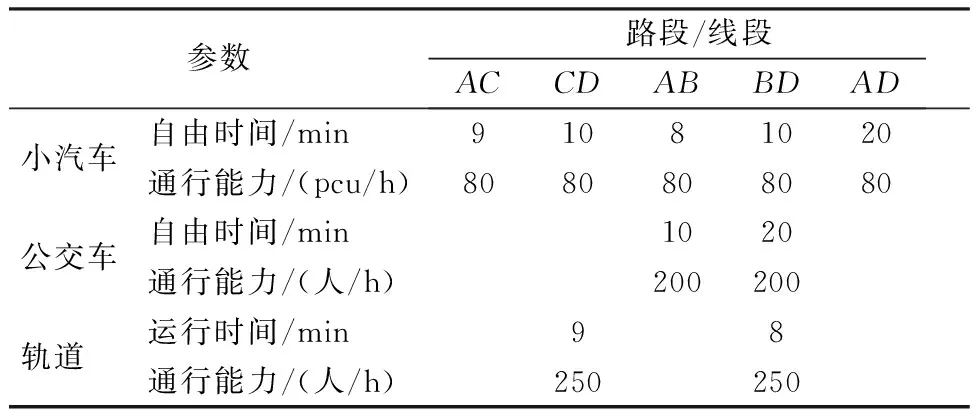
参数路段/线段ACCDABBDAD小汽车自由时间/min91081020通行能力/(pcu/h)8080808080公交车自由时间/min1020通行能力/(人/h)200200轨道 运行时间/min98通行能力/(人/h)250250

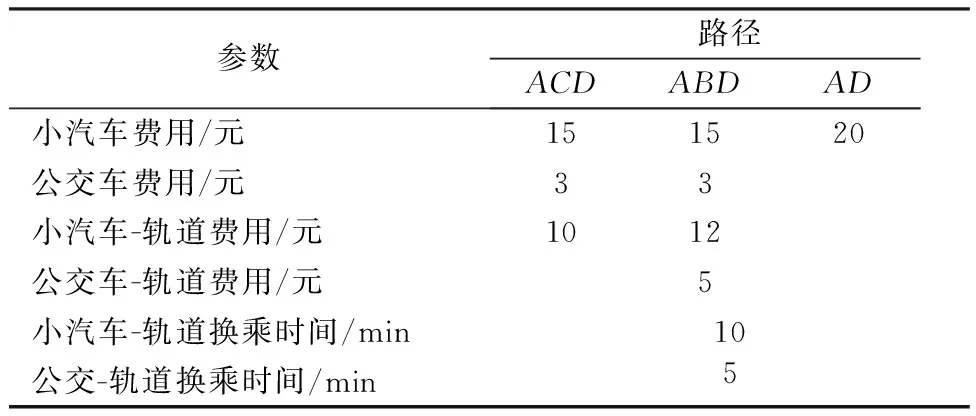
表2　复合网络路径特征参数Tab.2　The path characteristic parameters of composite network

表3　出行链阻抗参数Tab.3　Impedance parameters of the travel chain

将以上复合网络转为3级网络形式，见图6。由图6可见，共有4种交通方式(见图6 b))，其中小汽车-轨道有2种换乘方式(B点，C点换乘)(见图6 c))，小汽车出行有3条路径选择(见图6 a))。

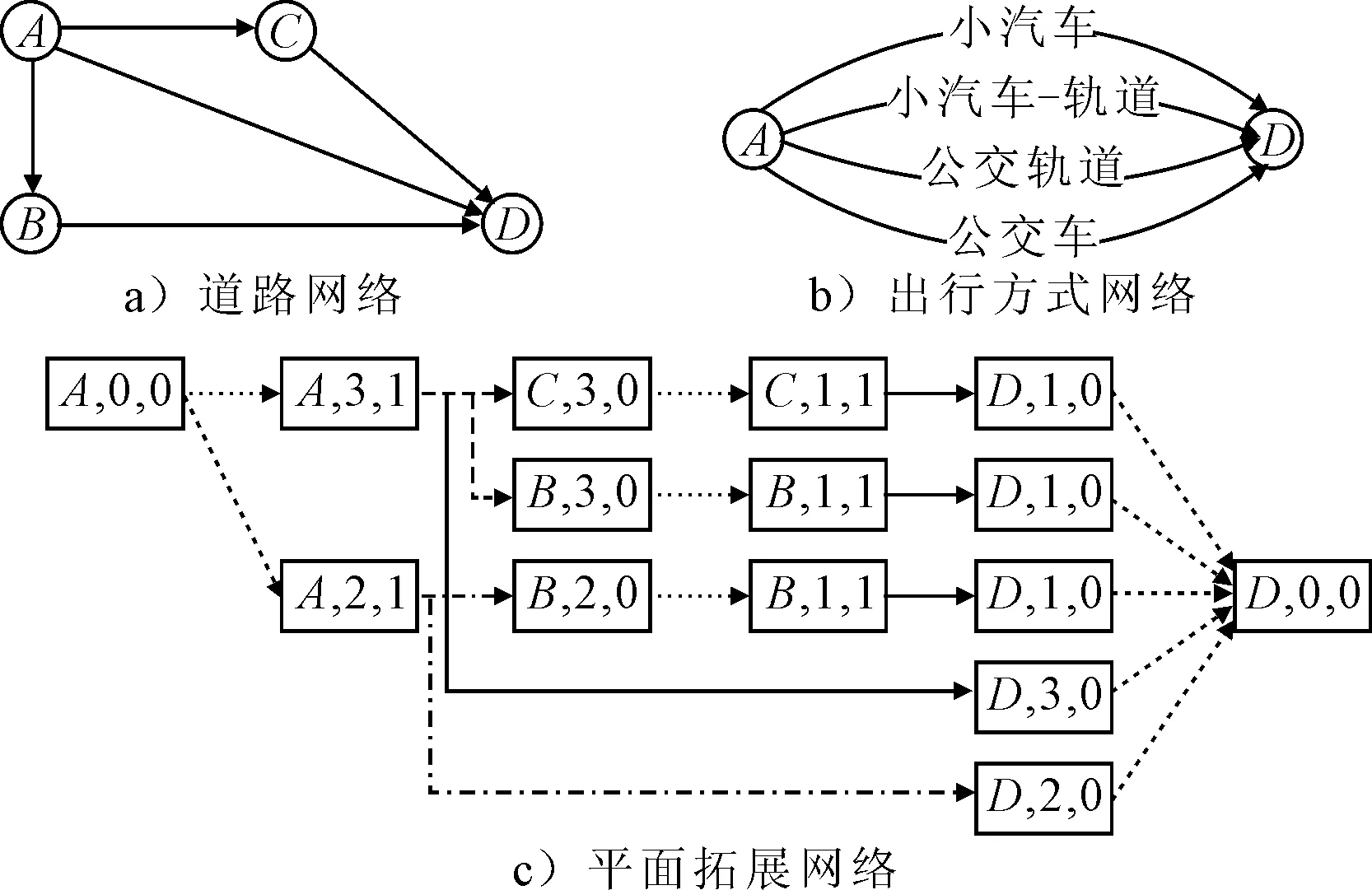
图6　多级网络结构Fig.6　The structure of multi-level network

利用matlab编程，计算得到迭代11次达到收敛条件(路段流量平均值为最后3次平均值，即9,10,11次)。

(26)

图7为算法收敛性检验。表4为第10次迭代结果。

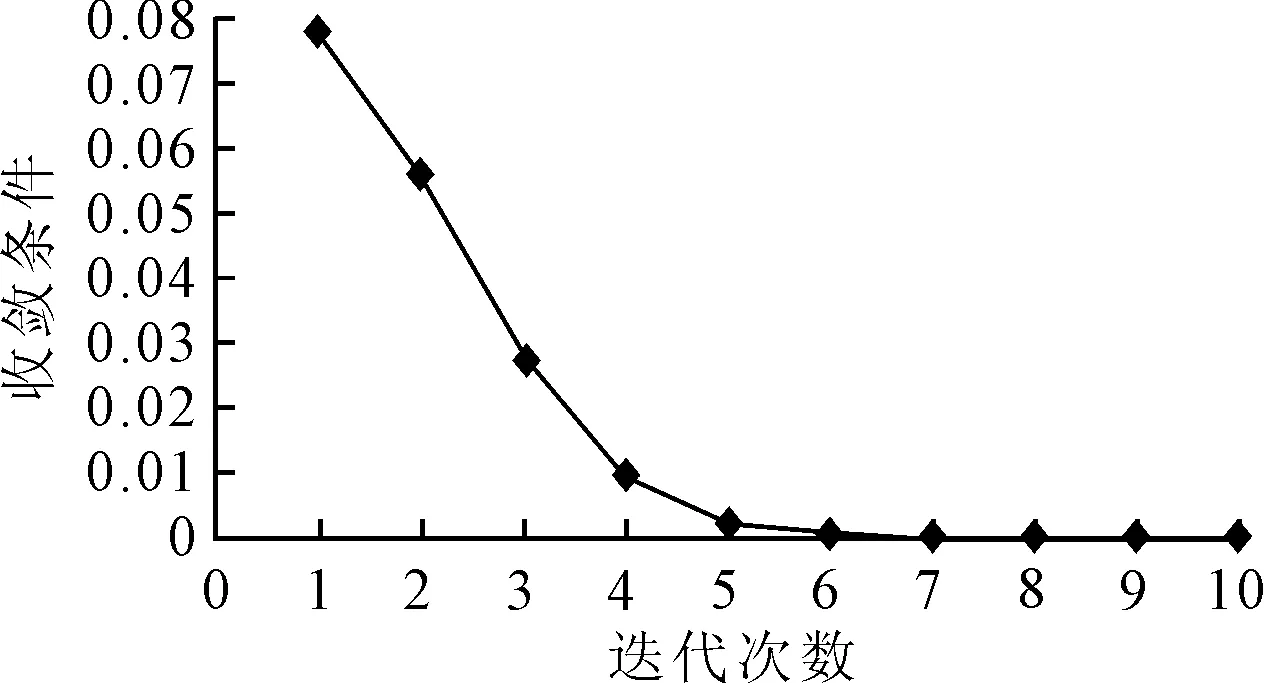
图7　算法收敛性检验Fig.7　Algorithm convergence test

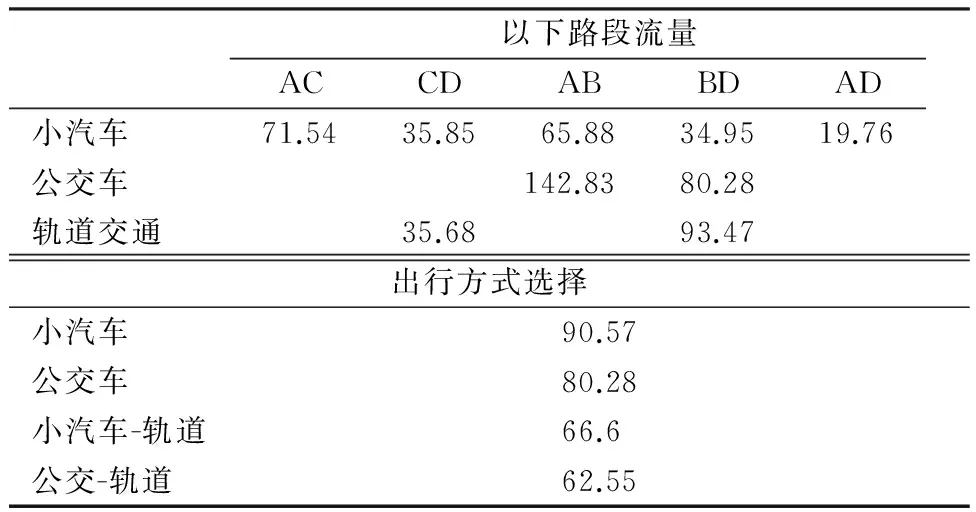
表4　第10次迭代结果Table4　The 10th iteration results　　人次/h

笔者设计情景SP调查验证该方法的可靠性，将图5表述为：从山东建筑大学新校区到老校区有4条路线，开车出行，公交换乘出行，公交-轨道，小汽车-轨道(C点换乘)和小汽车-轨道(B点换乘)，并按照表1，表2提供各条出行路线的综合费用。以问卷形式随机选择100人进行调查，调查结果见表5。

对比表4和表5可以看出，2种方法的方式选择结果基本一致，SP调查是基于出行者出行效用最大化意愿，结果较为粗略。而多级网络需求预测结果可以反映更多信息。例如，AB段流量高于AC段流量，BD段流量高于CD段流量，原因在于路径ABD比路径ACD提供更多的出行方式，具有更大的出行效用，因此,具有更大的吸引力，更多的人选择了ABD路径方式出行。而从小汽车出行来看却正好相反，AC流量略高于AB，CD流量略高于BD，说明多模式出行在吸引客流的同时，也减少了小汽车交通流量，有利于缓解道路交通压力。轨道交通出行虽然需要换乘，但出行时间小于公交车、出行费用小于小汽车，因此具有一定的竞争力，从A到D的出行中，有129人选择轨道交通换乘出行，占总需求的43%。

表5　出行方式选择SP调查结果Tab.5　Results of SP investigation of mode split　人次/h

5　结束语

多模式网络是由小汽车网络、公交网络和轨道网络等模式子网以及各模式子网之间的换乘构成的复合网络。多级网络流量配流模型，是将各模式的交通需求分为交通方式选择、换乘点选择和路径选择等多级网络需求，以出行效用最大化为原则将交通需求在各级网络的“路径”上进行分配，得到不同方式网络的交通流量。相比于传统的配流方法，多级网络配流可以直接将人次分配到复合网络上，并且考虑了出行选择的逻辑关系，使分配结果更加贴近现实。但是，多级网络需要有完整的出行链结构，这在局域复合网络中有一定的局限性，今后更加专注于解决局域多模式复合网络配流问题，并力争将模型与算法通过编程，作为仿真模块，完善现有规划软件，实现复合网络分配的快速性与集成性。

参考文献References

[1]晏克非.交通需求管理理论与方法[M].上海：同济大学出版社,2012.

YAN Kefei. Theory and method of traffic demand management[M].Shanghai:Tongji University Press,2012.(in Chinese)

[2]PALLOTTINO N. Hyperpaths and shortest Hyperpaths[J].Lecture Notes in Mathematics,1986(1403):258-271.

[3]LOZANO A, STORCHI G. Shortest viable hyper-path in multi-modal networks[J]. Transportation Research B,2002,36(10):853-874.

[4]FERNANDE Z, CEA E, FLORIAN J D, et al. Network equilibrium model with combined model[J]. Transportation Science,1994(28):182-192.

[5]CIPRIANI E, GORI S, PETRELLI M. Transit network design: A procedure and an application to a large urban area[J]. Transp Ortation Res Earch, Part C,2012(20):3-14.

[6]LO H K, YIP C W, WAN K H. Modeling transfer and non-linear fare structure in multi-modal network[J]. Transportation Research Part B,2001(12):149-158.

[7]胡文婷,陈 峻,王 炜.城市多模式道路网设计方法：模型 算法和应用[J].交通信息与安全,2015,33(2):20-25.

HU Wenting, CHEN Jun, WANG Wei. An approach of multimodal network design：models, algorithms and application[J]. Journal of Transport Information and Safety,2015,33(2):20-25.(in Chinese)

[8]孟 梦,邵春福.组合出行模式下多方式交通流分配模型及算法[J].吉林大学学报，2014(1):47-53

MENG Meng, SHAO Chunfu. Multi-modal traffic equilibrium model and algorithm with combined modes[J]. Journal of Jilin University,2014(1):47-53.(in Chinese)

[9]曹雄赳,贾洪飞,伍速锋,等.基于DAG-SVM的居民出行方式选择模型[J].交通信息与安全,2016,34(5):108-114.

CAO Xiongjiu, JIA Hongfei, WU Sufeng, et al. A model decision process of travel modes based on DAG-SVM[J]. Journal of Transport Information and Safety,2016,34(5):108-114.(in Chinese)

[10]张小宁.交通网络拥挤收费原理[M].合肥:合肥工业大学出版社,2009.

ZHANG Xiaoning. Theories of congestion pricing in transportation networks[M]. Hefei: Hefei University of Technology Press,2009.(in Chinese)

[11]谢 辉,于晓桦,晏克非.城市道路交通网络系统容量评估模型[J].中国公路学报,2012,12(3):129-134.

XIE Hui, YU Xiaohua, YAN Kefei. Evaluation model of urban road network system capacity[J]. China Journal of Highway and Transport,2012,12(3):129-134.(in Chinese)

[12]谢 辉.城市交通网络系统容量模型研究[D].上海:同济大学,2009.

XIE Hui. The systems capacity model of urban transportation network[D]. Shanghai: Tongji University,2010.(in Chinese)

[13]王红霖,焦朋朋,孙文博.基于元胞自动机的动态路段走行时间计算模型[J].交通信息与安全,2015,33(2):69-73.

WANG Honglin, JIAO Pengpeng, SUN Wenbo. Travel time estimation on dynamic links based on cellular automation[J]. Journal of Transport Information and Safety,2015,33(2):69-73.(in Chinese)

[14]王 华.复杂条件下的交通网络设计方法研究[D].上海:同济大学,2009.

WANG Hua. Research on transportation network design method under complex conditions[D]. Shanghai: Tongji University,2012.(in Chinese)

[15]关宏志.非集计模型:交通行为分析的工具[M].北京：人民交通出版社，2004.

GUAN Hongzhi. Disaggregated model-Tools for analysis of traffic behavior[M]. Beijing: People′s Communications Press.2004.(in Chinese)

[16]LEE Yusin, LU Lisin, WU Meiling, et al. Balance of efficiency and robustness in passenger railway timetables[J]. Transportation Research Part B： Methodological,2017,97(3):142-156.

[17]钱 臻,陆化普.一种公交网络客流分配方法及其实用性研究[J].清华大学学报(自然科学版),2005,45(9)：1170-1174.

QIAN Zhen, LU Huapu. An assignment method for transit network and its practical application[J]. Journal of Tsinghua University (Science and Technology Edition),2005,45(9):1170-1174.(in Chinese)

[18]黎冬平.城市轨道枢纽车站衔接交通资源的配置优化技术[D].上海：同济大学,2010.

LI Dongping. Optimization technology of the configuration of join transportation resources at urban rail passenger station[D]. Shanghai: Tongji University,2010.(in Chinese)