基于数学方法的缓和曲线地段建筑限界加宽值的研究
杨松尧
(辽宁铁道职业技术学院,辽宁 锦州 121000)
在铁路线路的设计过程中,缓和曲线地段内的内外侧加宽值计算基本采用以下两种方法:一是先计算圆曲线范围内的加宽值,然后将这个加宽值沿缓和曲线的长度均匀分摊,这种方法运算简单,但是计算值精度并不高;二是采用图形法,即在AutoCAD中绘制出缓和曲线的线型和列车车体位置,利用CAD系统的测量命令得到所需的加宽值,虽然这种方法计算值的精度高,但是实际运算非常复杂。随着对客运专线和磁浮铁路研究的深入,在客运站内站线的曲线也需要配置缓和曲线,所以沿到发线设置高站台时需要对缓和曲线范围内的建筑限界加宽值进行详细测算,传统的两种方法在进行计算时都有一定的缺陷。本研究通过采用解析几何等数学方法,提出了缓和曲线范围内的建筑限界加宽值计算公式,并对公示进行了推导。
1 缓和曲线地段建筑限界内加宽的计算思路
研究考虑了两种情况下求解内加宽值的方法,如图1所示。
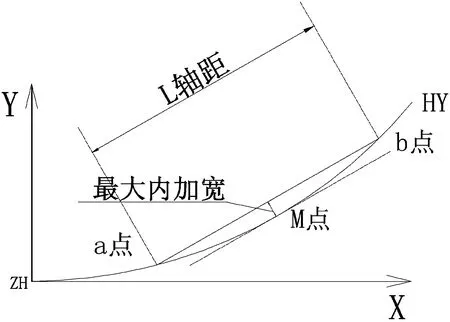
图1 求解内加宽值的方法
(1)根据已知的车辆后轴所在位置求此时车体对应的最大内加宽值及对应此内加宽值的点在缓和曲线上的位置。求解的主要思路如下:
第一步:根据车辆后轴(a点)的坐标(xa,ya)以及函数F(xa,ya)求得车辆前轴(b点)距ZH点的距离Lb以及坐标(xb,yb)。
第二步:根据第一步得到的a点、b点距ZH的距离La、Lb,找到在缓和曲线(圆曲线)上在{La,Lb}范围内的所有点中距直线ab的距离与外轨超高加宽之和最大的一点。
①当l≤l0时,该点的坐标可以由缓和曲线的计算方程得到。此时关于l的方程可表示为f(l)=getDistancePtLine(x1,y1,xa,ya,xb,yb)+Hhl/1 500l0,其中H为站台高度,h为曲线外轨超高值。
②当l>l0时,该点坐标可以由圆曲线的方程得到。此时关于l的方程可表示为f(l)=getDistancePtLine(x1,y1,xa,ya,xb,yb)+Hh/1 500,其中H为站台高度,h为曲线外轨超高值。
③采用一维黄金分割搜索法求出f(l)在{La,Lb}值域范围内的极大值,从而得到最大内加宽值及M点距ZH点的距离。
(2)求缓和曲线上任意一点(M点)对应的最大建筑限界内加宽值以及此时车辆后轴所处的位置。主要思路是找到当车辆后轴处于某一位置时,车轴连线的斜率与该点的切线斜率相同。具体求解步骤概述如下:
第一步:先求出当车辆后轴(a点)位于ZH点时车辆前轴(b点)所处坐标,得到此时车轴连线的斜率K0。
第二步:将M点对应的切线斜率K与K0相比较,K
①当K ②当K>K0时,可以先假设a点的坐标为(xa,ya),xa=l-l5/40C2+l9/3 456C4,ya=l3/6C-l7/336C3+l11/42 240C5, b点坐标可由函数F(xb,yb)得到,此时关于l的方程f(l)为(ya-yb)/(xa-xb)=K,展开后为f(l)=l11/42 240C5-Kl9/3 456C4-l7/336C3+Kl5/40C2+l3/6C-Kl+Kxb-yb。 可以通过二分法求出f(l)=0时l的值进而得到a点的坐标。进而通过M点距AB直线的距离加上外轨超高产生的内加宽值Hhl/1 500l0获得M点处最大内加宽值。 研究考虑了两种情况下求解外加宽值的方法,如图2所示。 图2 求解外加宽值的方法 (1)根据已知的车辆后轴所在位置求此时车体对应的最大外加宽值及对应此外加宽值的点的位置。计算的主要思路是在缓和曲线或圆曲线上求得一点,使得该点与车体边缘连线的点对应的切线垂直。具体求解步骤概述如下: 第一步:根据车辆后轴(a点)的坐标(xa,ya)以及函数F(xa,ya)求得车辆前轴(b点)距ZH点的距离Lb以及坐标(xb,yb)。 第二步:根据车轴至车体边缘的距离Lcd以及车轴的斜率计算出车体边缘的c点和d点的坐标(xc,yc),(xd,yd)。 第三步:判断c点和d点的投影点是否位于缓和曲线的长度范围内,如果这两点的x坐标都小于0说明肯定不在缓和曲线范围内,反之可以先得到HY点与圆心点连线在Y轴上的交点(M点),判断c点或d点与M点、ZH点之间的夹角。当夹角角度大于缓和曲线切线角β0时说明投影点落在圆曲线范围内,小于β0说明投影点落在缓和曲线范围内。 ①先假设最大外加宽处在缓和曲线上的投影点E点的坐标为(xe,ye),xe=l-l5/40C2+l9/3 456C4,ye=l3/6C-l7/336C3+l11/42 240C5,当E点处切线的斜率K1=tg(l2/2Rl0)与直线ED的斜率K2=(ye-yd)/(xe-xd)满足K1×K2=-1时,说明两线垂直。则关于l的方程为f(l)=K1l11/42 240C5+l9/3 456C4-K1l7/336C3-l5/40C2+K1l3/6C+l+K1yd-xd。 可以通过二分法求出f(l)=0时l的值进而得到E点的坐标。进而通过E点距AB直线的距离获得最大外加宽值。 ②如果投影点E点落在ZH点前的直线上时,可直接将E点至直线的垂距定为外加宽值,如果投影点E点落在HY点后的圆曲线范围内,则圆心至E的距离减去曲线半径即为外加宽值。 (2)求缓和曲线上任意一点(M点)对应的最大建筑限界外加宽值及此时车辆后轴所处的位置。主要思路是找到当车辆后轴处于某一位置时,车体边缘与M点连线的斜率与M点所处缓和曲线的切线斜率相垂直。具体求解步骤概述如下: 第一步:先求出M点的切线斜率K1,并假设车辆后轴(a点)所处位置距ZH点l米处,由函数F(xa,ya)得到a点坐标(xa,ya)和车辆前轴(b点)坐标(xb,yb)。 第二步:根据a点、b点的坐标得到车体边缘的C点和D点的坐标(xc,yc),(xd,yd)。 第三步:用二分法求解方程(yM-yc)/(xM-xc)K1=-1,其中xc、yc都有关于l的方程f(l)。 第四步:l值求出后通过计算M点至直线AB的距离即可得到最大外加宽值。 本研究通过采用解析几何、微积分等数学方法并结合计算机编程来解决缓和曲线范围内的建筑限界加宽值详细计算问题。研究了曲线地段建筑限界加宽值计算所需的公式,对各项参数进行逐项分解,据此算法编制的程序可以针对具体车型计算曲线(包含缓和曲线)上任意点最大内外加宽值,以及指定最大内外加宽值时计算车体所处的位置,在实际应用中对建筑设计及施工有较大的指导意义。 [1]周兵和.铁路曲线限界加宽研究[J].铁道标准设计,2013(4):20-26. [2]赵振刚.铁路建筑限界缓和曲线地段加宽研究[J].铁道标准设计,2017,61(5):16-22. [3]李明炜.对铁路站场到发线曲线地段建筑限界加宽方法的探讨[J].铁道标准设计,2017,61(2):10-13. [4]温双义.铁路客运站台建筑限界曲线和过渡段的加宽研究[J].高速铁路技术,2016,7(4):24-29. [5]朱礼佳.关于缓和曲线可侵入站台范围长度的初步研究[J].交通与运输(学术版),2016(2):68-71.2 缓和曲线地段建筑限界外加宽的计算思路
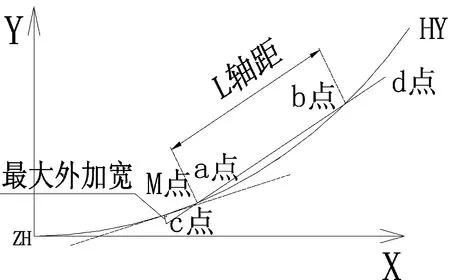
3 结束语

