粘滞质量阻尼器模型的频域与时域分析

,　　

(天津大学 建筑工程学院，天津　300350)

0　引言

最近几年，关于惯性质量阻尼器的应用在逐渐增加，相对以前的变刚度和变阻尼控制系统，粘滞质量阻尼器(Viscous Mass Damper,VMD)的出现成为一种可选的阻尼器类型，丰富了抗震形式，该装置利用滚珠丝杠将直线运动转化为高速的旋转运动，这种节点间的相对运动在产生阻尼力的基础上，还产生惯性力。常规的惯性质量装置，如调谐质量阻尼器[1](Tuned Mass Damper，TMD)，多运用于降低由风载和地震引起的结构反应。其中，VMD和TMD都通过改变振动方程的惯性力部分来改善系统的反应。两者也有不同之处，TMD需要很大的质量和很大的空间，VMD可以通过改变转子的尺寸获得很大的等效质量，因此，VMD利用更小的空间获得相同的质量，同时，TMD可以与主体结构发生共振，所以置有TMD的结构要承受大位移。Saitoh[2]研究惯性质量装置在基础隔震系统中的位移控制效果。Hwang et al[3]提出了具有滚珠丝杠放大机制的旋转惯性阻尼器(Rotational Inertia Damper，RID)的振动控制系统。Saito et al[4]研究具有惯性质量的粘滞阻尼器结构的反应控制。Ikago et al[5]提出了一种新型的抗震控制装置，调谐质量粘滞阻尼器(Tuned Mass Viscous Damper，TMVD)，该阻尼器就是本文研究的VMD的拓展，并将TMVD运用到单自由度系统中研究它的性能。

1　粘滞质量阻尼器的力学模型

图1　粘滞质量阻尼器示意图

如图1所示，VMD通过滚珠丝杠的旋转产生很大的阻尼力和惯性力[5]。本文研究VMD的惯性效应和阻尼效应，基于参考文献[5]的研究成果，忽略摩擦力，VMD可以简化为一个惯性单元和一个阻尼单元，如图2所示。为更好地研究VMD的性能，将结合单自由度系统进行研究，这种单自由度系统类似于基础隔震系统，简化为一个集中质量，并附加有阻尼力和弹簧恢复力，多自由系统可以等效成单自由度系统。

图2　VMD的力学模型

(1)

2　置有VMD的单自由度系统

基于参考文献[5]的TVMD模型，忽略摩擦力，本文提出3种不同配置有VMD的单自由度系统，阻尼器模型1、2、3分别如图3～图5所示。采取无量纲参数化研究，对3种单自由度系统进行频域[6]和时域分析。在时域分析中，无量纲的参数化主要借鉴频域分析的结果。

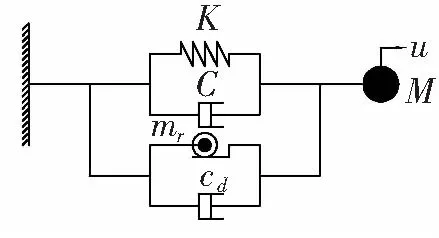
图3　阻尼器模型1

图4　阻尼器模型2

图5　阻尼器模型3

2.1　配有VMD的单自由度系统的频域分析

2.1.1阻尼器模型1

(2)

方程(2)可以写成下面的形式

(3)

(4)

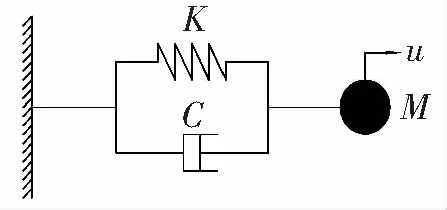
图6　传统阻尼器模型

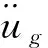
(5)

(6)

假定阻尼系数hs=0.1、hc=0.2和自振频率fs=0.25 Hz，绘出方程(4)表示的共振特性。方程(3)中其它的参数满足

(7)

图7　hs=0.1、hc=0.2及fs=0.25 Hz的阻尼器模型1

图7(a)中，随着质量比β的减小，相对位移u显著减小，同时，共振频率向低频移动，即VMD延长结构的周期。从图7(b)看出，在结构共振区之外，随着质量比的减小，加速度反应逐渐增大。因此，虽然置有VMD的单自由度结构能够显著降低相对位移，但也引起加速度反应的增大，因此，模型1有必要进一步优化。

2.1.2阻尼器模型2

阻尼器模型2是阻尼器模型1的有益改进，图4将一个弹簧单元kb和VMD串联与单自由度结构结合。其中，弹簧单元的作用主要是降低VMD在高频区的效应，提高单自由度结构的减振性能。在地面加速度作用下，阻尼器模型2的运动方程

(8)

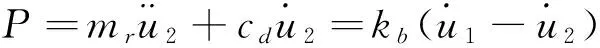
(9)

假定某稳态激励的圆频率是ω，阻尼器模型2的动态刚度(Dynamic Stiffness)

(10)

在地面加速度作用下，阻尼器模型2的等效方程

(11)

假定简谐激励，图4所示系统的稳态响应可以写成

(12)

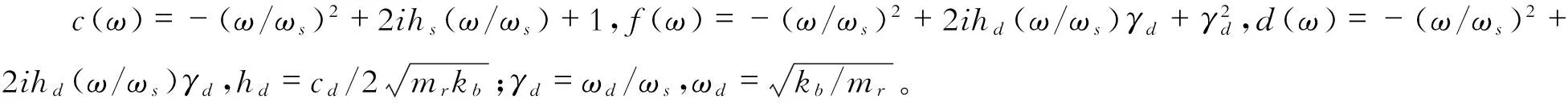
阻尼器模型2中，假定阻尼系数hd=0.2和频率比γd=1.0，其它的假定与图7相同，绘制地面位移与质点响应的放大率关系图，见图8，随着质量比的下降，有两个明显的放大区域：低频的放大区域主要是由VMD和单自由度结构引起的共振；高频的放大区域主要是由弹簧单元和单自由度结构引起的共振。图8(b)表明超过高频区的共振频率后，随着激励频率的增加，加速度反应趋向于零。这些性质表明弹簧单元与VMD相连能够减少VMD在高频区的影响，因此，基于弹簧单元的ωd，可以调整导致VMD效应降低(高频区加速度增大效应)的高频区域的频率值。

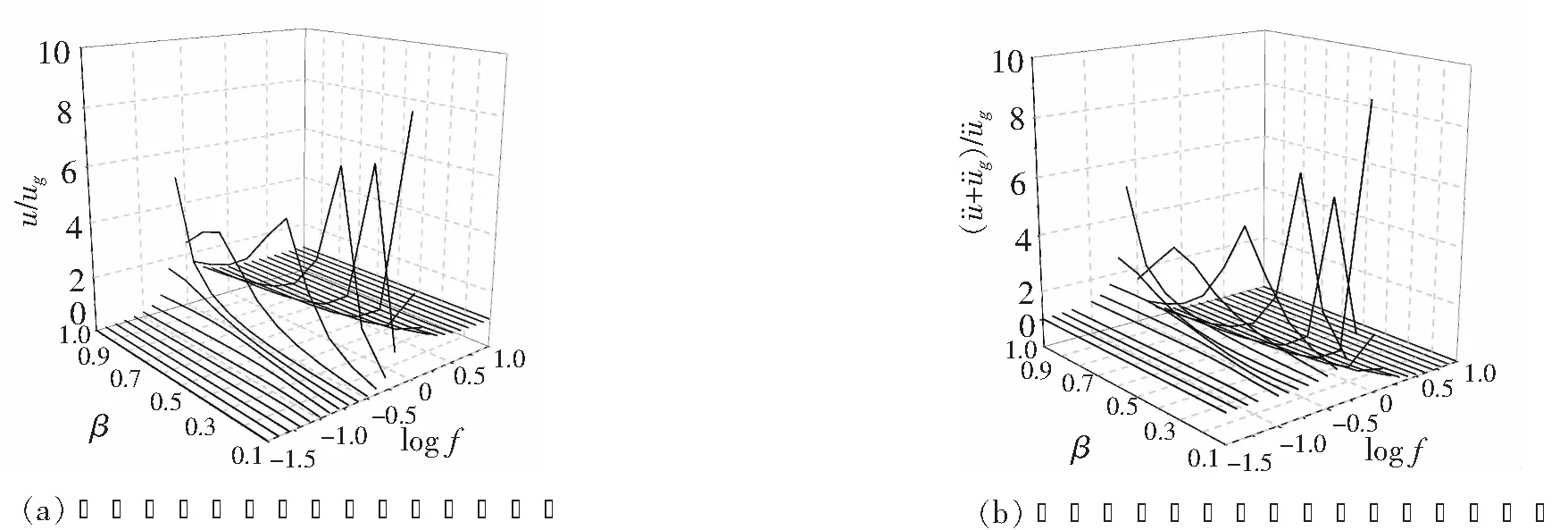
图8　hs=0.1、hd=0.2、γd=1.0及fs=0.25 Hz的阻尼器模型2

2.1.3阻尼器模型3

与阻尼器模型2不同，阻尼器模型3增加了一个阻尼单元，如图5，阻尼单元主要吸收由弹簧单元和单自由度系统产生的第二放大区域的地震能量，适用于长周期地震波作用下的区域。如同阻尼器模型2，假定某稳态激励的圆频率为ω，阻尼器模型3的动态刚度

(13)

式中，cb是与弹簧单元并联的阻尼器的阻尼系数。

(14)

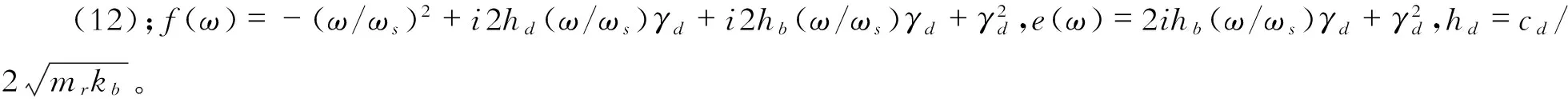
假定阻尼系数hb=0.2，其它的参数与图8相同，绘出方程(14)表示的共振特性。图9可以看出，在第二放大区域，将阻尼器与弹簧单元并联组成弹簧/阻尼单元能够明显降低相对位移和加速度反应。

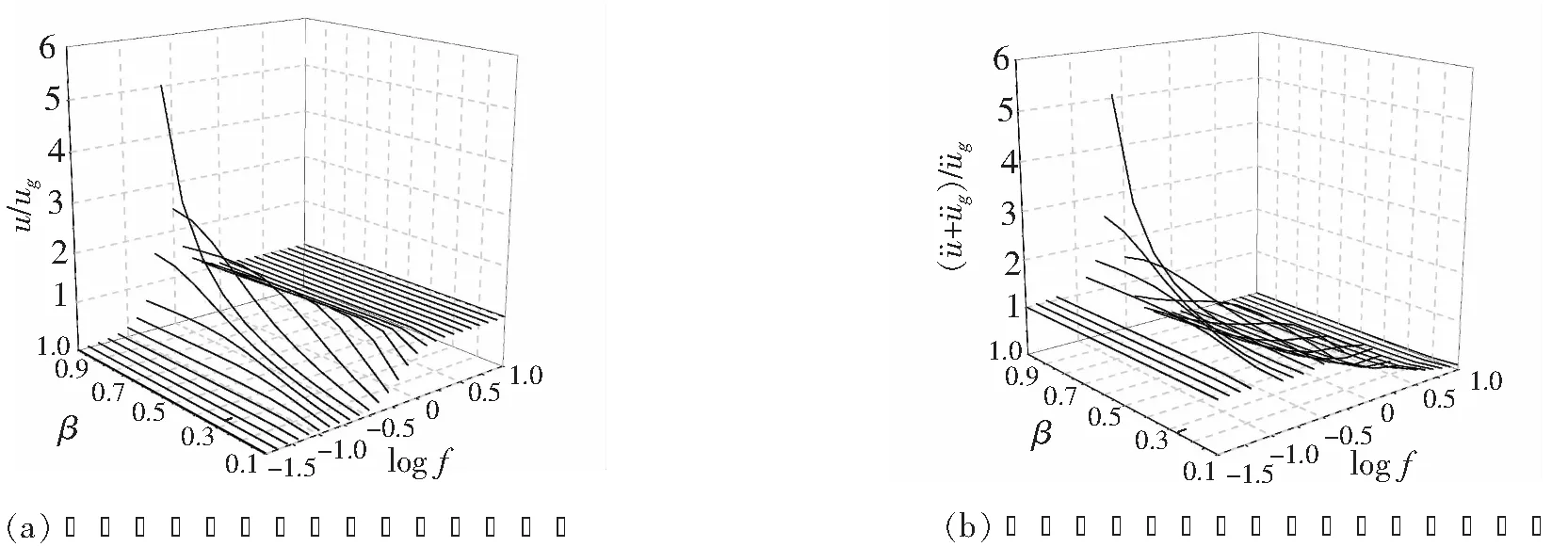
图9　hs=0.1, hb=0.2,hd=0.2, γd=1.0, β=0.5和fs=0.25 Hz的阻尼器模型3

2.2　置有VMD的单自由度系统的时域分析

利用实际地震纪录，对上述系统进行时程分析来验证VMD装置的减振效果。阻尼器模型1和传统阻尼器模型是单自由度结构，其运动方程分别是方程(3)、方程(5)，同样地，阻尼器模型2和阻尼器模型3是双自由度结构，因此，矩阵形式的运动方程可以很好地评估时程反应。阻尼器模型2的运动方程如下

(15)

式中，u1和u2分别是单自由度体系中结构质量与VMD等效质量的相对位移，如图4。方程无量纲化

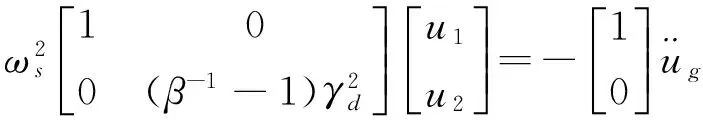
(16)

同样地，模型3的运动方程如下

(17)

方程(17)无量纲化后，得到

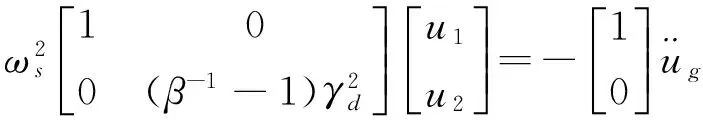
(18)

时程分析采用线性加速度的Newmark-β法，Δ=0.005 s，加到模型中的地面加速度纪录如下：(1)Lucerne(1992)，(2)Managua(1972)，(3)Chi-Chi(1999)(如图10)。可以看出：Lucerne有最大的加速度幅值的脉冲时程；Chi-Chi有长周期效应的脉冲时程；Managua则有上面两者之间的幅值和短周期效应的时程。时域分析所需的参数与前面的频域分析的参数相同，hs=0.1，hb=0.2，hd=0.2，γd=1.0，β=0.5和fs=0.25 Hz。

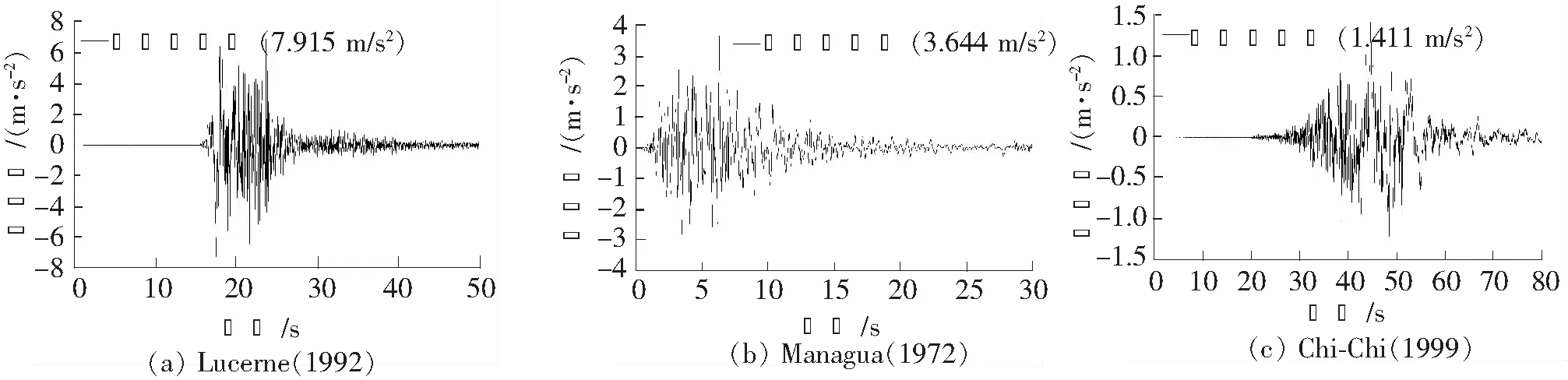
图10　时域分析的地震纪录的时程

图11　传统模型与其它模型的最大反应幅值

图12　传统模型与其它模型的反应幅值比对比

图12(a)可见，阻尼器模型1和3均有效地降低了相对位移(模型1幅值比59%)。而Managua则由于其包含的频率成分扩大了阻尼器模型2的相对位移(模型2的相对位移比传统模型大69%)。对于Chi-Chi来说，即长周期地震下，图11和图12表明模型3能够显著地降低相对位移和加速度反应。图12(b)表明，Lucerne所包含的频率成分导致阻尼器模型1、2和3的共振(模型1的最大加速度甚至达到3.912 m/s2)。阻尼器模型2的提出，初衷是为了解决阻尼器模型1导致的高频区加速度增大的问题，虽然相对位移和加速度都在随质量比减小，但总体仍呈增大趋势。在长周期时程作用下，模型3的相对位移幅值比是56%，加速度幅值比是71%，可见，模型3中，弹簧/阻尼单元与VMD串联可以有效地降低结构的相对位移和加速度反应。

3　结论

(1)忽略摩擦力效应，依据VMD的力学模型，提出了3种置有VMD的模型，阻尼器模型延长了结构的自振周期。

(2) 通过频域分析和时域分析，模型3既有效地降低了结构的相对位移，又有效地降低了结构的加速度反应，适用于长周期地震作用下的抗震结构。在Chi-Chi等长周期地震时程作用下，模型1没有显著地减少结构的相对位移及加速度反应，因此，在软土场地，应该小心地使用该类型阻尼器元件。

[1]王淼，顾萍．半穿式钢桁梁桥横向振动TMD阻尼减振研究[J]．石家庄铁道学院学报，2006，19(1)：14-17．

[2]Saitoh M. On the performance of gyro-mass devices for displacement mitigation in base isolation systems[J]. Structural Control & Health Monitoring, 2012, 19(2):246-259.

[3]Hwang J S, Kim J, Kim Y M. Rotational inertia dampers with toggle bracing for vibration control of a building structure[J]. Engineering Structures, 2007, 29(6): 1201-1208.

[4]Saito K, Sugimura Y, Inoue N. A study on response control of a structure using viscous damper with inertial mass[J]. Journal of Structural Engineering, 2008, 54:623-648.

[5]Ikago K, Saito K, Inoue N. Seismic control of single-degree-of-freedom structure using tuned viscous mass damper[J]. Earthquake Engineering & Structural Dynamics, 2012, 41(3): 453-474.

[6]涂文戈，邹银生．MTMD减震结构体系的频域分析[J]．工程力学，2003，20(3)：78-88．