天津软土地区深基坑多级支护结构变形的参数分析

　，　　，　

(1.天津大学 土木工程系，天津　300072；2.滨海土木工程结构与安全教育部重点实验室，天津　300072)

0　引言

随着我国城市化进程的加快，城市人口日益增加，可利用的土地资源随之减少，因此地下空间开发的力度逐渐增大，许多深大基坑也随之产生。在软土地区，基坑工程的周边场地条件复杂，土质条件差，基坑支护结构型式的合理选用以及基坑施工过程对于基坑工程的变形控制十分重要[1-3]。目前深基坑工程的支护体系主要采用的是地下连续墙结合水平支撑的形式，这些临时支护结构存在着造价高，施工周期长，不可循环利用等问题。因此发展更加经济且环保的无支撑支护技术具有十分重要的意义。

目前在软土地区的基坑工程中，无支撑多级支护技术已得到运用，如：上海虹桥综合交通枢纽基坑工程[4]和天津中铁房地产金钟河大街项目基坑[5]等。近年来，已有一些学者对多级支护结构展开了研究。郑刚等[6]对无支撑多级支护结构稳定性与破坏机理分析进行了研究，发现无支撑多级支护体系在方案合理的情况下，次级支护结构可以有效抑制主要支护结构被动区塑性剪切带的开展，各级支护结构协同工作能力良好，整体稳定性强，失稳破坏后最终形成一个经过主要支护结构下部的圆弧形滑动面，破坏模式类似于重力式悬臂厚挡墙。任望东等[5]对深基坑多级支护破坏模式及主要几何参数的影响进行了数值计算分析。郑刚等[7]对大面积基坑多级支护结构进行了研究，研究发现当两级支护之间宽度较小时，多级支护的工作机制和破坏机制近似于异形重力式挡土墙，可产生整体式破坏；而随着多级支护之间的宽度增大，土体的破坏面可进入多级支护的围护桩之间的土体，并使多级支护桩的破坏产生相互关联的影响，产生关联式破坏；当多级支护的宽度足够大时，多级支护可产生分离式破坏。上述研究均是针对多级支护的稳定性问题，而对于多级支护的变形特征研究较少。

另一方面，文献[7]总结了多级支护的不同形式及使用范围，提出了倾斜桩在多级支护中应用的可能。在倾斜桩的研究方面，郑刚等[8-9]对倾斜单排桩和前排桩倾斜的双排桩在水平荷载作用下的性状进行了研究。

为了研究多级支护几何参数对其变形的影响，本文运用大型通用有限差分软件FLAC3D对天津某基坑工程采用的无支撑多级支护结构进行了计算分析，将数值计算结果与实测结果进行了对比验证。在此基础上采用简化的数值模型对第二级支护结构长度、两级支护间距离、两级开挖深度比以及第一、二级支护结构的倾角等几何参数进行了计算分析。计算结果表明，多级支护几何参数对变形的影响并不独立。实际工程中，应根据场地条件，变形控制及造价的要求综合考虑多级支护参数的选择。

1　工程概况及数值模拟模型

1.1　工程概况

本工程位于河北区狮子林大街与海河东路交口处，拟建工程包括14栋多层及高层住宅楼及多栋公用配套建筑，整体1层地下室，局部2层地下室。基坑的总开挖面积为50 600 m2，1层地下室处的基坑开挖深度为7.0 m左右，2层地下室处的基坑开挖深度在8.8～10.3 m之间，其中局部电梯坑处的开挖深度达到12.3 m，基坑开挖面近似为五边形，且基坑四周均有建筑物和道路，基坑平面示意图见图1。

由于基坑面积较大，采用常规排桩+水平支撑形式时，水平支撑造价高工期长，因此为了不设置水平支撑，采用了双排桩结合单排桩的多级支护形式，如图1、图2所示。第一级支护结构为前后排桩长均为26.4 m的双排灌注桩，前排桩采用Φ1 000@1 400灌注桩而后排桩采用Φ900@1 400灌注桩，双排桩排距为3.6 m，帽梁厚度为0.9 m，且在前后排桩之间有长度为24.2 m的Φ850@900的三轴水泥搅拌桩作为止水帷幕。第二级支护结构为Φ800@1 000的单排灌注桩，桩长为13.4 m，帽梁厚度0.6 m。两级支护间距离在3.8～9.0 m之间。两级支护桩及帽梁均采用C30混凝土。

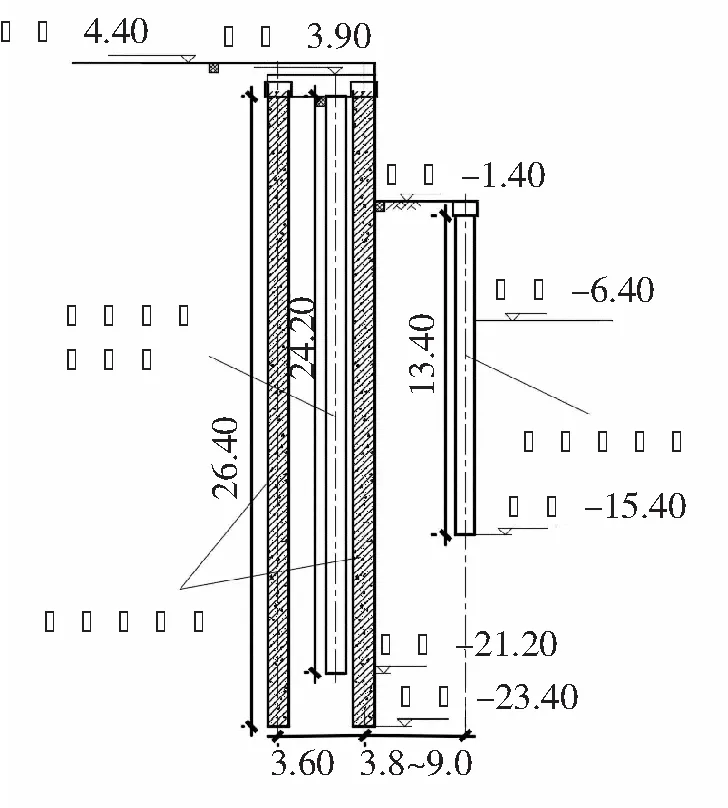
图2　无支撑多级支护结构(单位：m)

1.2　数值模型

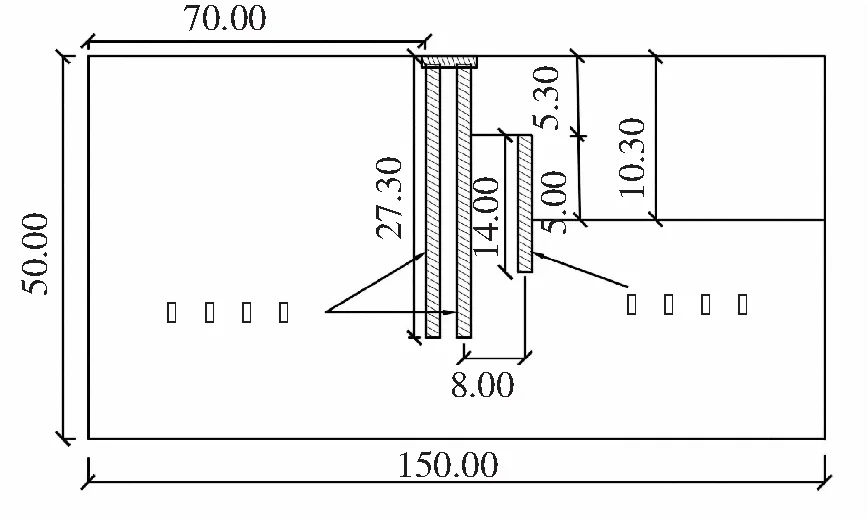
图3　计算剖面(单位：m)

本文采用有限差分软件FLAC3D对该基坑的多级支护结构进行数值分析，考虑到基坑面积大，计算剖面的长度较大，符合平面应变特征，因此采用二维平面应变模型进行分析。根据资料可知，为了消除边界效应对计算结果的影响，基坑外侧的宽度宜控制在开挖深度的3～5倍以上[10]；取模型的总尺寸为150 m×50 m，基坑外侧宽度为70 m。第一级开挖深度为5.3 m, 第二级开挖深度为5.0 m；双排桩(第一级支护结构)前后排长度均为27.3 m，单排桩(第二级支护结构)长度为14 m，两级支护间距离取8 m。根据现场勘查结果，取模型地下水位位于地面以下1 m。模型两侧约束水平位移，底部约束水平和竖向位移。计算剖面如图3所示。

土体本构模型采用CYsoil模型。CYsoil本构模型是建立在莫尔库仑模型之上的双屈服模型，考虑了在(p,q)平面内的椭圆形帽盖屈服面。椭圆轴的比率α取决于K0的值。该模型可以考虑帽盖硬化、摩擦硬化及压缩/膨胀硬化准则。该模型中的指数m取0.9，泊松比μ为0.2，校准系数β取2.36，失效比Rf取0.9[11]。各土层的计算参数见表1。基坑双排桩的前后排桩及单排桩分别根据抗弯刚度等效原则等效为挡土墙。采用衬砌结构单元(liner)进行模拟，第一级支护结构等效厚度取1.0 m，第二级支护结构等效厚度取0.9 m，重度为24 kN/m3，弹性模量为30 GPa，泊松比为0.2。双排桩前后排桩的连梁采用梁单元(beam)模拟，支护结构与土体之间为摩擦接触，界面摩擦角和黏聚力的值取相邻土体参数的0.7倍[12-13]。

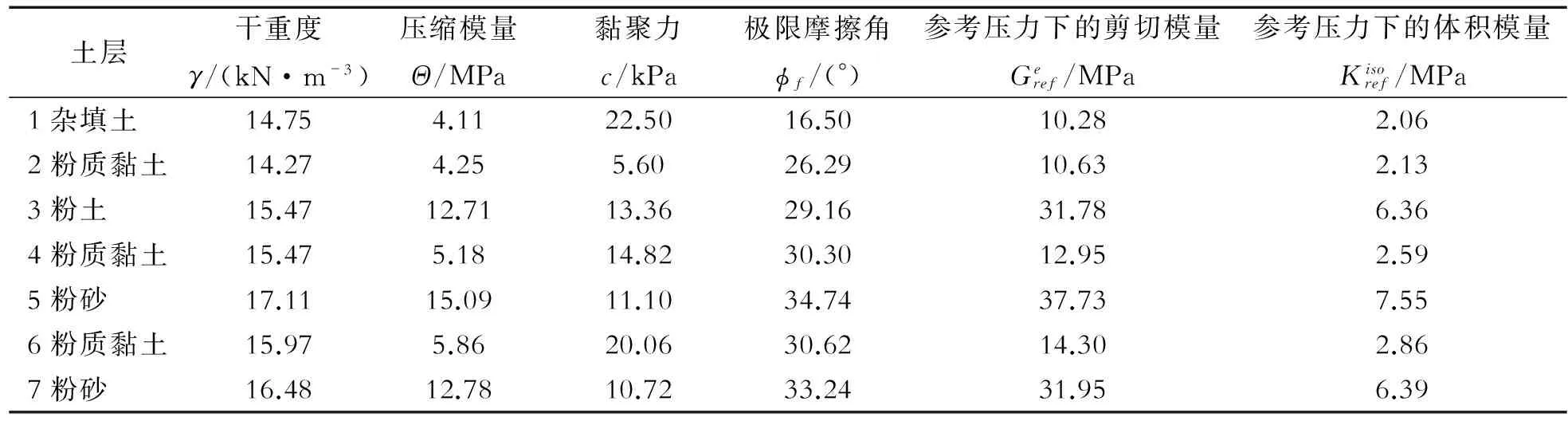
表1　土体CYsoil模型参数

数值模拟全过程分为5步：第1步建立土体单元，进行地应力平衡；第2步建立支护结构单元，并将初始位移清零(不考虑围护结构施工影响)；第3步将水位降至地表以下12.3 m处；第4步进行第一级开挖至地表以下5.3 m；第5步进行第二级开挖至地表以下10.3 m[14]。

1.3　计算与实测数据对比

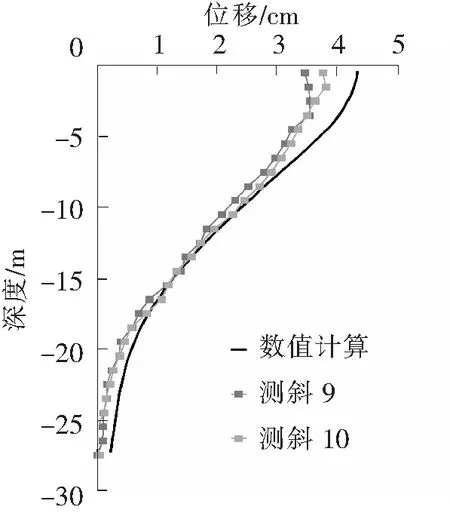
图4　实测数据与计算结果对比

为了监测基坑开挖过程中多级支护的变形情况，在基坑西侧采用多级支护的位置布置了两根测斜管，监测基坑开挖过程中作为第一级支护的双排桩前排桩的水平位移。基坑的桩身水平位移监测点9和测点10位于基坑西侧(位置见图1)。

数值计算得到的水平位移与实测结果的对比如图4所示。数值模拟中的第一级桩身的最大位移值为4.32 cm，工程实测的测点9的最大水平位移为3.59 cm，测点10的最大水平位移为3.82 cm，数值计算结果与实测结果接近。与一般悬臂支护不同，实测及计算的位移曲线均出现了桩身下部向坑内弯曲而上部向坑外弯曲的特征。这主要是由于桩顶的冠梁对桩身上部的变形起到了约束作用。数值计算与实测结果的对比表明了数值模型的可靠性，CYsoil本构模型很好地反映了基坑开挖过程中围护结构的变形特征。

2　无支撑多级支护结构变形参数分析

图5　简化计算模型(单位：m)

2.1　简化数值模型

为了进一步研究多级支护几何参数对变形的影响，建立简化的数值模型进行分析计算。如图5所示，简化模型第一、二级支护结构均为地下连续墙。计算模型整体尺寸取100 m×50 m，基坑外侧宽度取40 m，总开挖深度8 m，不考虑超载和放坡的影响。模型的两个侧边约束水平位移、底部约束水平和竖向位移。

由于郑刚[8-9]等的试验及数值分析指出，相对于竖直围护桩，具有一定倾斜角的围护桩可产生更小的水平位移和更小的内力，因此相同条件下具有一定优势，所以本文在第一级、第二级支护桩也考虑了桩倾斜的情形。

为了消除实际中土层性质差异的影响，简化模型采用单一土层进行分析。本次计算选取了表1中天津地区典型的粉质黏土(土层4)进行计算。模型中的地连墙采用厚度为1 m的liner单元模拟，其重度为24 kN/m3，弹性模量为30 GPa，泊松比为0.2。

2.2　参数分析

因为坑内支护结构的变形受多种因素综合影响且一般工程中主要关心基坑最外围支护结构的变形，所以本文只研究基坑的两级开挖深度比H1/H2，第二级支护结构长度L2，两级支护间距离B。θ1为第一级支护桩倾角，θ2为第二级支护桩倾角。上述几何参数分析的具体取值范围见表2。

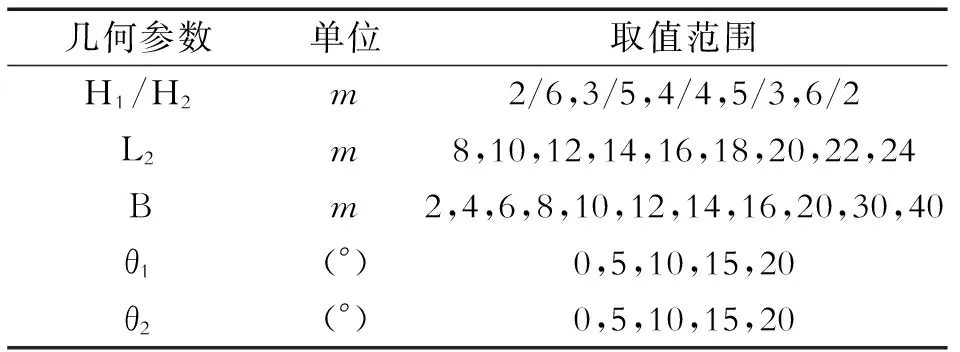
表2　几何参数取值范围

2.2.1两级支护间距离B

对第一级支护结构长度L1取20 m，第二级支护结构长度L2取12 m，不同开挖深度比H1/H2时，两级支护间距离B对第一级支护结构水平位移最大值影响如图6。可以看到，当B/H小于2.0时，水平位移随着B的增加急剧下降，对于B/H小于1.0时，位移减小幅度则更大；而B/H大于2.0时，水平位移减小的幅度较小，逐渐趋于平缓，并趋近于与第一级开挖深度相等的悬臂开挖所产生的最大水平位移。以图6(c)为例，当B/H由0.25增加到1.0时，第一级支护结构水平位移减小约112%，B/H由1.0增加到2.0时，则减小约24%，而B/H由2.0增加到5.0时，则仅减小了13%。对于L2不同的情况，B的影响一致。

由以上分析可知，对于天津软土地区的无支撑多级支护结构，两级支护间距离B对支护结构的变形影响显著。当两级支护间距离B小于1倍开挖深度时，第一级支护结构的最大水平位移较大，最大位移随着B的增加而迅速减小；当B大于2倍开挖深度时，继续增大B，不能明显减小第一级支护结构的最大水平位移；当B介于1倍和2倍开挖深度之间，增大B可有效地减小第一级支护结构的最大水平位移。

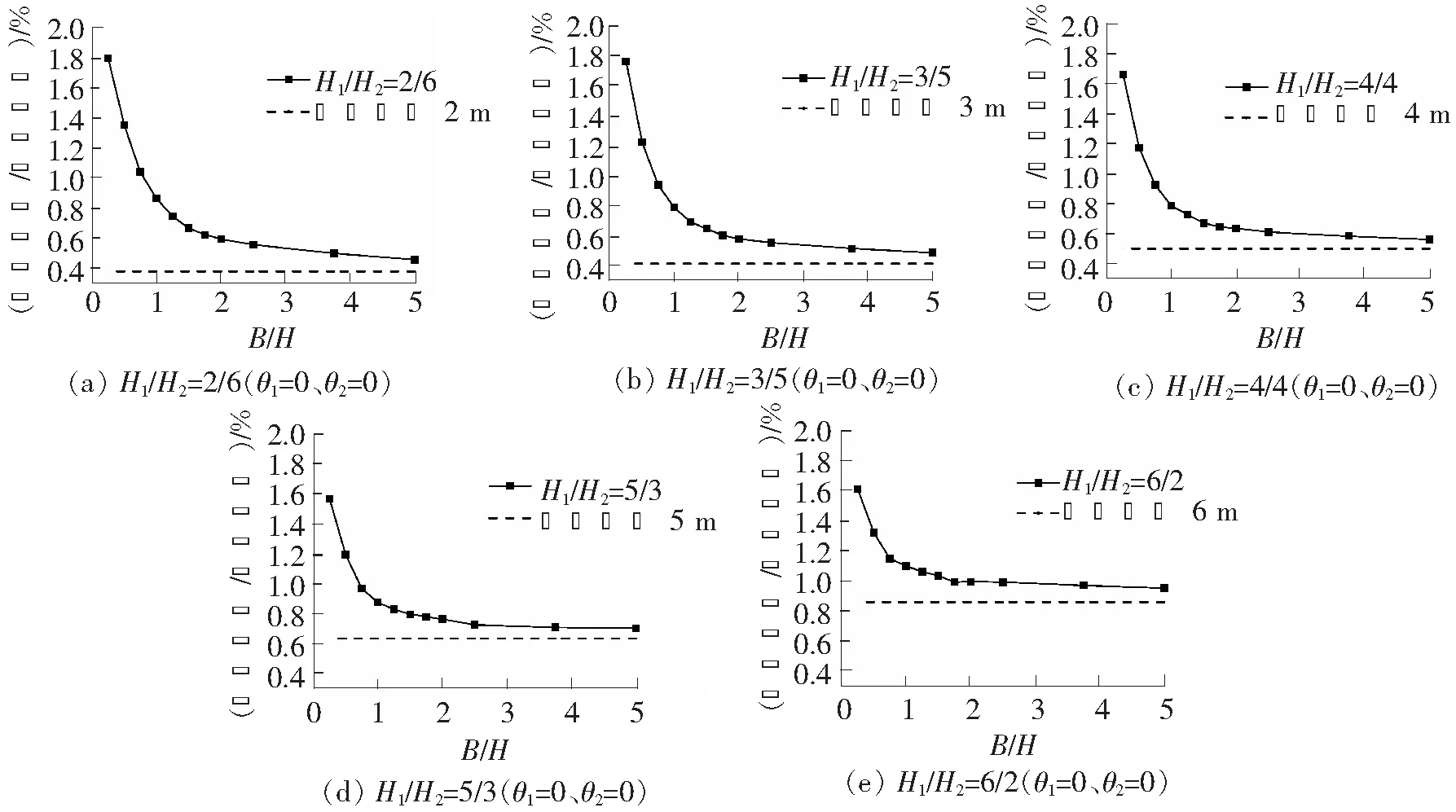
图6　两级支护间距离B与第一级支护最大水平位移关系

2.2.2开挖深度比H1/H2

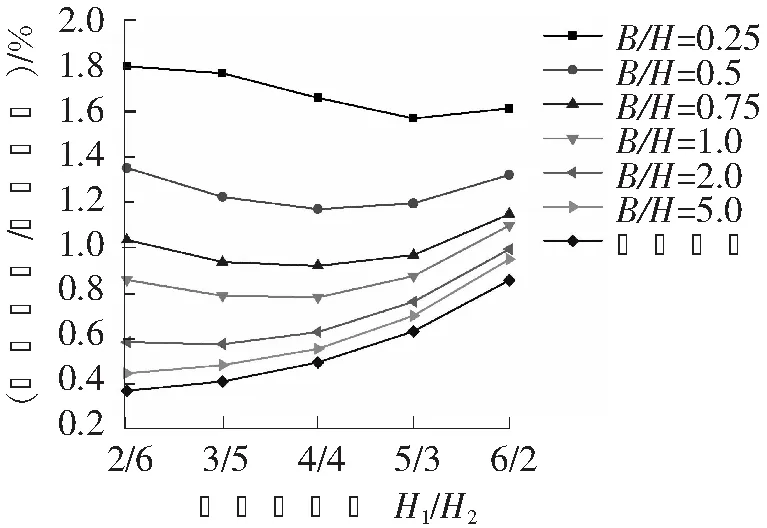
图7　开挖深度比H1/H2与第一级支护最大水平位移关系

图7所示为第一级支护结构长度L1为20 m，第二级支护结构长度L2为12 m时，开挖深度比H1/H2与第一级支护结构最大水平位移的关系(θ1=0,θ2=0)。图中显示了两级支护间距离B不同时，H1/H2的影响情况。作为对比，计算了仅存在第一级支护的情况下分别开挖2 m、3 m、4 m、5 m、6 m的最大水平位移情况(图中曲线‘悬臂开挖’)。

从图7可以看到，对于B/H非常小(B/H=0.25)的情况，H1/H2为5/3时第一级支护水平位移取得最小值。当B/H处于0.5～1.0之间时，H1/H2取4/4时第一级支护水平位移最小。而当B/H大于2.0，则第一级开挖深度越小，水平位移值越小。出现上述情况的原因是：由于第二级支护结构长度L2固定为12 m，则意味着第二级开挖深度越大，第二级支护结构的插入比越小，则第二级支护的水平位移越大，而第一级支护的水平位移受到第二级支护的影响。另一方面，第一级开挖深度越大，第一级支护水平位移越大。这是一对矛盾的因素，多级支护结构的优化即在于选择适当的开挖深度比，使得第一级支护的水平位移受到第二级开挖影响较小，又要避免第一级开挖造成的第一级支护位移不会太大。

当B/H为0.25时，两级支护结构间距很小，第二级开挖的影响很大，是主要矛盾，因此出现第一级支护水平位移随开挖深度比增加而减小的情况。而对H1/H2为6/2时的位移增大，则是第一级开挖成为主要矛盾导致的。

当B/H取0.5～1.0之间时，两级基坑的开挖有着较强的相互影响，无论哪一级支护结构出现较大位移都会影响另一级支护结构，而由于两级支护结构的刚度是相同的，因此两级基坑开挖深度接近时，各自位移大小也比较一致，此时可以取得较小的位移。

当B/H大于2.0时，两级基坑开挖的相互影响较弱，B/H越大则越接近只有第一级支护结构的悬臂开挖的情况。因此，此时第一级开挖深度是主要矛盾，第一级开挖深度越小，位移越小。

从上述分析中可以看到，开挖深度比H1/H2对变形的影响与两级支护间距离B有关。在两级支护结构刚度接近的情况下，如果B很小时(小于0.5倍开挖深度)，开挖深度比越大，第一级支护结构的最大水平位移越小；如果B大小适中(0.5～2.0倍开挖深度)，两级开挖深度越接近，第一级支护结构的最大水平位移越小；如果B较大(2.0倍开挖深度以上)，开挖深度比越大，第一级支护结构的最大水平位移越大。

但是，对于减小第一级开挖深度的方法，实际是以增加第二级支护结构的变形(尤其是对B较大的情况)为代价的。因此，更合理的开挖深度分配应该是根据两级支护结构的刚度及嵌固深度不同，使刚度较大或嵌入深度较大的一级支护结构支挡较大的开挖深度。对于刚度接近或嵌固效果相当的情况，则适宜选择均匀分配开挖深度。

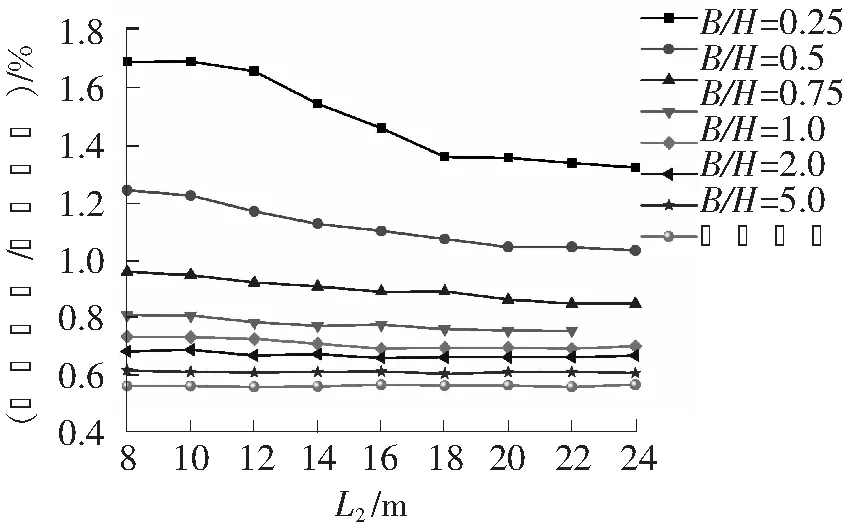
图8　第二级支护长度L2与第一级支护最大水平位移关系

2.2.3第二级支护结构长度L2

当第一级支护结构长度L1为20 m开挖深度比H1/H2为4/4时，不同的两级支护间距离B情况下第二级支护结构长度L2对第一级支护最大水平位移的影响如图8所示。可以发现只有当B很小时，L2才对位移有较大影响。这主要还是因为B值较大时，第二级支护变形对第一级支护影响减小。当B值大于1.0倍开挖深度时，L2变化的影响就几乎可以忽略了。又由图8可知，在B很小(B/H=0.25)的情况下，L2的增加最多使位移减小了28%，并且L2的增加只是在一定范围内影响较大，当第一和第二级支护结构底部等深度时，继续增加L2对水平位移的影响就很小了。

因此，当两级支护间距离B较大时，增加第二级支护结构长度L2，对于控制第一级支护结构的最大水平位移的影响不大；只有在两级支护间距离B很小的情况下，且在一定范围内增加第二级支护结构长度L2，才可比较有效地控制第一级支护结构的最大水平位移。

2.2.4第二级支护结构倾角θ2

为了研究第二级支护结构倾角θ2对第一级支护结构的最大水平位移的影响，设两级支护间距离B为4 m，开挖深度比H1/H2取4/4，第一级支护支护结构长度L1为20 m，第一级支护结构倾角θ1为0°时，第二级支护结构长度L2为12 m，第二级支护结构倾角θ2分别取0°、5°、10°、15°和20°时，得到第二级支护结构倾角θ2与第一级支护结构的最大水平位移的关系曲线，如图9所示。

由图9可知，当第二级支护结构倾θ2从0°增大到20°时，第一级支护结构的最大位移减小了25.44%，且二者几乎呈线性相关。由此可知，增大第二级支护结构倾角θ2，可有效地控制第一级支护结构的最大水平位移。

2.2.5第一级支护结构倾角θ1

保持两级支护间距离B为4 m，开挖深度比H1/H2为4/4，第一级支护结构长度L1取20 m，第二级支护结构倾角θ2为20°，第二级支护结构长度L2为12 m，第一级支护结构倾角θ1分别取0°、5°、10°、15°和20°时，得到第一级支护结构倾角θ1与第一级支护结构的最大水平位移关系曲线，如图10所示。

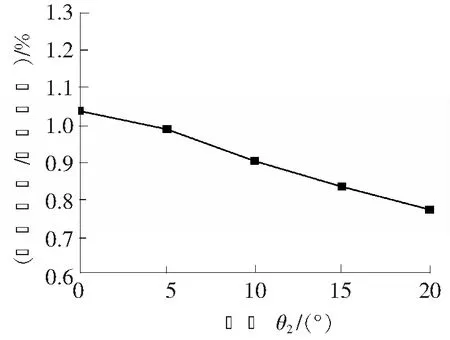
图9　第二级支护倾角θ2与第一级支护的最大水平位移关系

图10　第一级支护倾角θ1与第一级支护最大水平位移的关系

由图10可以看出，当第一级支护结构倾角θ1从0°增大到20°时，第一级支护结构的最大水平位移值减小了39.97%。由此可知，增大第一级支护结构倾角θ1，对于减小第一级支护结构的最大水平位移值的作用明显。

3　结论与建议

采用数值方法对天津软土地区的大面积深基坑无支撑两级支护结构的变形特性进行分析，得到以下结论：

(1)两级支护间距离B是影响支护结构变形的主要因素，当两级支护间距离B小于1倍开挖深度时，第一级支护结构的最大水平位移随着B的增大而迅速减小；当两级支护间距离B介于1倍和2倍开挖深度时，第一级支护结构的最大水平位移会随着B的增大而减小，但减小的幅度较小；当两级支护间距离B大于2倍开挖深度时，继续增大B，不能有效地减小第一级支护结构的最大水平位移。

(2)开挖深度比H1/H2对支护结构变形的影响，受两级支护间距离B影响。在B很小的情况下，在一定范围内增大开挖深度比H1/H2，第一级支护结构的最大水平位移减小，但当H1/H2过大时，位移将会增大；如果B大小适中(0.5～2.0倍开挖深度)，两级开挖深度越接近，第一级支护结构的最大水平位移越小；如果B较大(2.0倍开挖深度以上)，开挖深度比越大，第一级支护结构的最大水平位移越大。

(3)第二级支护结构长度L2对支护结构变形的影响不大，且与两级支护间距离B有关。当两级支护间距离B较大时，增加第二级支护结构长度L2对减小第一级支护结构的最大水平位移的作用不大；只有在两级支护间距离B很小的情况下，且在一定范围内增加第二级支护结构长度L2，第一级支护结构的最大水平位移会随着L2的增大而减小。

(4)支护结构的倾角对支护结构变形影响很大。在支护结构倾角不大于20°的情况下，增大第一级支护结构倾角θ1和第二级支护结构倾角θ2，第一级支护结构的最大水平位移值将减小，且二者几乎呈线性关系。

[1]龚晓南. 关于基坑支护的几点思考[J]. 土木工程学报, 2005,38(9): 99-102.

[2]刘志明，付强，朱正国，等. 深大基坑施工过程三维数值模拟分析[J]. 石家庄铁道大学学报：自然科学版，2013,26(增刊)：208-211.

[3]王世清，林森斌. 某深基坑工程邻近桥梁桩基施工影响分析[J]. 石家庄铁道大学学报：自然科学版，2013,26(增刊)：95-104.

[4]翁其平，王卫东. 多级梯次联合支护体系在上海虹桥综合交通枢纽基坑工程中的设计与实践[J]. 建筑结构，2012，42(5)：172-176.

[5]任望东，张同兴，张大明，等. 深基坑多级支护破坏模式及稳定性参数分析[J]. 岩土工程学报,2013,35(增刊2): 919-922.

[6]郑刚，程雪松，刁钰. 无支撑多级支护结构稳定性与破坏机理分析[J]. 天津大学学报,2013,46(4): 304-314.

[7]郑刚，郭一斌，聂东清，等. 大面积基坑多级支护理论与工程应用实践[J]. 岩土力学, 2014,35(增刊2): 290-298.

[8]郑刚，白若虚. 倾斜单排桩在水平荷载作用下的性状研究[J]. 岩土工程学报,2010,32(增刊1): 39-45.

[9]徐源，郑刚，路平. 前排桩倾斜的双排桩在水平荷载下的性状研究[J]. 岩土工程学报, 2010,32(增刊1): 93-98.

[10]Burland J B,Sim Poon B J. Movements around excavations in London Clay[J]. Design Parameters in Geotechnique Engineering, 1979, 1: 13-29.

[11]Ngoc-Anh D, Daniel D, Pierpaolo O, et al. 3D modelling for mechanized tunnelling in soft ground-influence of the constitutive model[J]. American Journal of Applied Sciences, 2013, 10 (8): 863-875.

[12]Potyondy J G. Skin friction between various soils and construction materials[J]. Geotechnique, 1961, 11(4): 339-353.

[13]Acer Y B, Durgunoglu H T, Tumay M T. Interface properties of sands[J]. Journal of the Geotechnical Engineering Division, 1982, 108(4): 648-654.

[14]孙二小，赵玉成. 渗流-应力耦合作用下基坑开挖变形性状分析[J]. 石家庄铁道大学学报：自然科学版, 2015, 28(4):48-52.