感悟数学的“有趣”“好玩”“很美”——“洛水神龟献奇图”教学实录与评析

□ 阮江豪 执教 宋华良 评析

【教学内容】小学数学拓展性课程之数学文化系列——“洛水神龟献奇图”（幻方）。

【教学目标】

1.通过想一想、画一画、写一写的数学过程，培养学生发现问题、提出问题、动手实践、合作交流、尝试调整的能力，提升学生的数学思维，渗透数形结合的数学思想，体验事物之间都存在联系的易经哲学思想。

2.经历对洛书的探索解读，理解三阶幻方中“幻和是多少”和“五居中央”的奥秘。

3.学生感受中国文化的博大精深和数学的独特魅力。

【教学过程】

一、观图——引出洛书

师：（课件出示课题）同学们，看到这个题目，你有什么想问的？

生：什么是洛水神龟？

生：奇图是怎么样的一幅图？

师：就让我们带着这些疑问来观看这段视频。（学生认真地观看视频）

师：视频已经放完，现在你又有什么想说的？

生：我知道了奇图是怎么来的。

生：我知道了奇图就是神龟背上的图案。

生：洛书就是神龟上的图案。

师：今天我们就一起来看看这个奇图洛书，它有什么神奇的地方呢？

课件出示：

生：这幅图上的有些圆圈是涂黑的，有些是白色的。

生：涂黑的圆圈在四个角上，是2个，4个，6个和8个。

生：这边有2个点就代表数字2，4个点就代表数字4……（学生将各个点所代表的数字一一表述出来）

课件出示：

师：这些数阵有什么奇特的呢？

生：每条边上的数加起来都是15，包括对角线上的数。

师：真的是15吗？

课件动画演示：

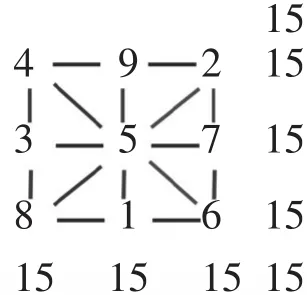
师：这洛书确实比较神奇！这9个数通过这样的排列组合，使得每行、每列和对角线上的数字之和都相等（板书）。

【评析】课堂伊始，让学生看着“令人疑惑”的数学内容，提出自己想提的问题，之后教师通过播放“大禹治水与洛书”的视频让学生“释疑”，并在这一过程中，学生经历从古代洛书到现代幻方的转变过程，由此读懂洛书所表现出来的数学现象，即每行、每列和对角线上的数字之和都等于15。观看视频的环节不仅引发学生浓厚的兴趣，更凸现其中的数学元素，情趣与理趣并存。

二、品图——探寻洛书的奥秘

师：是不是只有这样一种情况，使得每行、每列和对角线上的数字之和都相等呢？它们的和一定是15吗？谁能用这9个数字，再创造出一个与众不同的神奇洛书呢？请将你的想法写在练习纸上。（学生尝试）

师：我耳边传来修正带涂改的声音！看来同学们对自己的作品在不断地调整—尝试—调整，这是一种实用的数学学习方法。

师：有没有哪位同学愿意分享自己调整了好多次，但还是不成功的情况？

学生分享自己的作品：

师：你能否帮他调整一下，最好是数字尽可能少变动？

生：2和9对调，1和8对调，7和3对调。

师：这样调整就可以了吗？能否检验一下？

生：每行、每列和对角线上的和都是15。

师：同学们，看来通过调整可以使失败变成功！如果你刚刚还没有成功的，请你再试着调整；如果你刚刚已经成功的，请你思考还有其他的情况吗。

师：现在请成功的同学举手！（明显增多）

师：看来，当我们经历失败的时候，不应放弃，可以试着调整，从其他不同的角度来思考问题。

【评析】给学生充分的思考时间与空间，让他们在“尝试—失败—调整—成功”的体验中，增强探究数学问题的欲望与提升学习数学的信心。

师：你成功了吗？和是多少？

生：成功了，和是15。

师：此刻，老师在思考一个问题，为什么和一定是15？

生：因为中间一定是5。

生：如果把9个数都加起来是45，45除以9是5，因为有3个数，所以5乘3是15。

师：他们从不同的角度来思考这个问题，都很棒！现在，老师给你一个新的角度，你有什么想法？课件出示：

1+2+3+4+5+6+7+8+9=45

生：这样有3行，除以3，所以就是15。师：除了从行看，还能从其他角度看吗？生：每竖列也是这样，45除以3等于15。课件出示：

师：同学们，看来在这幅图中，每行、每列和对角线上的数字之和不仅相等，而且还都是15。其实像这样的图总共有8个。

课件出示：

师：观察这8个图，你有什么发现？

生：这些图中，中间的数是不变的，外面那圈数字一直在转，和还是一样的。

生：我发现4和2一直在同一行，8和6也在同一行，3和7也在同一行，9和1也在同一行。

生：每中间一横行和每中间一竖列都是1和9或者是3和7。

生：四个角上的数都是2，4，6，8。

师：你们的发现真多，还有什么问题想问的吗？

生：为什么四个角上都是2，4，6，8这些偶数？

生：为什么1，3，7，9都是包围着5？

生：为什么中间都是5？

生：外面这些数是怎么旋转的？

师：现在我们就来研究这些问题，首先研究为什么中间都是5。（学生4人小组进行交流讨论）

生：5是1到9的平均数，如果5不在中间，这个图是成不了每行每列和对角线上和是15的，所以5在中间。

生：1和9，2和8，3和7，4和6分别加起来是10，剩下5就是中间的。

生：可以用组合法，如果3个数加起来要等于15，5用到的次数最多，所以它就在中间。

师：5用到的次数最多是什么意思？

生：1到9这9个数字，加起来是15的算式中，用到5的算式最多。

师：用到5的算式有几个呢？

生：4个，1+5+9=15，2+5+8=15，3+5+7=15，4+5+6=15。

师：为什么5出现次数最多，有4次，在这幅图中就非得填中间？能否在图中表示出来？

学生板演并讲解：这4条线都经过中间，表示算式有4个，只有5在算式中出现了4次。

师：看来这样是出现的次数

最多，所以这个5必须在中间。这个问题我们已经解决了，你还想解决哪个问题？

生：为什么偶数都在四个角上？

生：为什么1，3，7，9都在5的上下左右？

师：其实这些奥秘都在老师给你提供的算式中，你等会可以试着去找找看。

【评析】正是有了问题，学生才有了主动探究的欲望，学生的思维才有了一定的方向。此环节中，学生通过观察、比较，发现三阶幻方的一些特点之后，教师给予学生一点启发，让学生提出问题。而在解决学生所提出的问题时，面对挑战性的学习任务，教师通过讨论、操作、尝试等活动，借助数形结合的数学思想，让学生在直观中明白、理解三阶幻方中“幻和”“中间数”的奥秘。找寻问题的“聚焦点”，使学生的思维得到活跃，这便是数学拓展课的思维性吧！

三、赏图——体会数学文化的独特魅力

师：这些神奇的图其实就是我们现在说的三阶幻方，你知道世界上研究幻方的第一人是谁吗？

课件演示：

杨辉：九子斜排，上下对易，左右相更，四维突出。

师：你看，这就是什么？

生：这就是“洛水神龟献奇图”。

生：这是洛书。

师：确实，这就是洛书。当然，洛书对中国文化的影响也非常大，咱们一起来看这个视频，以此来结束我们今天这节课。（播放视频：洛书对数学文化的影响与对中国古代都城规划的影响）

【评析】洛书作为世界上第一个发现的幻方，其代表着中国古代数学的伟大成就，阮老师通过课件演示杨辉的三阶幻方构造法和观看关于洛书对中国乃至世界数学文化影响的视频，使学生在增强民族自豪感的同时，获得数学文化知识，提升数学素养。

【总评】

本节课阮老师精心设计，选取特殊的题材，借助数学拓展课程，以洛书为载体，在活动中辅以数形结合的数学思想、万物皆有联系的易经哲学思想，使得学生通过比较分析、尝试调整、探索交流，理解洛书中的奥秘，更在课始与课尾通过视频的形式介绍中国的文化，以提升学生的数学素养。

在本课教学中体现数学拓展课的三个基本理念：（1）数学有趣。数学拓展课程不以知识与技能的习得为终极目标，而更重情感、态度、价值观目标的落实，通过拓展课教学，应让学生感受数学材料的有趣，数学思考的乐趣，从而改善数学与学生之间的关系；（2）数学好玩。拓展课更重视学生基本活动经验的积累，在动手操作、自主探索、合作交流的氛围中，创造性地解决数学问题，让学生体验“数学好玩”；（3）数学很美。通过多种资源跨学科的挖掘与整合，使学生在获得数学活动经验与思想的同时，更感受到数学文化的魅力与数学的博大精深，让学生由衷地赞叹数学之美。