面向城市建成区扩展模拟的CA-Markov模型改进
李 静,陈云波,刘小茜,裴 韬,施 昆,李向新,5
(1. 昆明理工大学国土资源工程学院,云南 昆明 650093; 2. 昆明市规划编制与信息中心,云南 昆明 650500;3. 中国科学院地理科学与资源研究所资源与环境信息系统国家重点实验室,北京 100101; 4. 北京联合大学应用文理学院,北京 100191; 5. 高原山区测绘技术应用工程研究中心,云南 昆明 650093)
进入21世纪以来,随着全球城市化的推进,中国处于快速城市化进程驱动的城市空间扩展阶段[1-2]。然而同时,城市无序蔓延、生态环境破坏、土地利用结构失衡、土地资源衰竭等负面影响也随之而来[3]。因此,探索城市扩张的机制和原理,开展城市扩展的时空动态模拟,是新型城镇化建设有效的决策支持过程,是谋求区域可持续发展的必然条件[4]。
元胞自动机模型(cellular autonomic,CA)是当前研究城市扩展和土地利用变化模拟预测的主要模型[5-6]。Wolfram等把CA模型称为“与牛顿发现的万有引力基本原理相媲美的科学金字塔”。20世纪70年代,Couclelis等[7]指出将CA模型首次应用在地理建模中,预测和模拟城市扩张及土地利用覆盖变化。CA模型有很高的空间分辨率和运算能力。与传统的模型相比,CA模型的优点还包括[8-9]:①空间性;②宏观与微观的关联性;③与GIS和RS技术的兼容;④动态性;⑤简单和可视化。城市扩展变化过程是一个复杂的非线性过程,而CA模型有一定的局限性,基于CA的城市模拟面临着一下问题:CA模型邻域像元仅由城市密度决定,考虑因素单一、随意;不同分辨率下所模拟的城市形态具有差异性。
为了进一步完善CA模型在预测方面的性能,对传统CA模型的许多限制条件放宽[10-12],近年来的土地研究中,更多学者将元胞自动机模型结合Aburas等[13]研究的层次分析(analytic hierarchy process,AHP)模型、逻辑回归模型[14-15]、马尔可夫链(Markov)模型[16-18],都得到了较好的研究成果。其中,CA-Markov模型得到众多应用。何丹等(2014)[19]整合CA和Markov链,再利用GIS和RS模型,与数据有效地融合,模拟预测城市扩展。Aburas等[13]研究芙蓉(马来西亚马来亚地区西南部城市)城市扩展预测,可以更好地实现模拟过程中元胞转换数据定量控制,验证了CA-Markov模型精度可达到83%。但在众多的对元胞自动机的放宽规则大多较为单一,为了有效地解决土地模拟中的相关问题,林坚等[20]提出了整合模型,即将不同的模型相结合来弥补单一模型的不足。
基于以上分析,本文提出了整合基于层次分析模型(AHP)、逻辑回归模型(logistic regression)构建指标权重系数的元胞自动机-马尔可夫链(CA-Markov)方法,来改进城市扩展适宜性图层。首先,AHP模型实现专家意见评价,LR模型实现数据定量化,Markov模型实现城市扩展预测,CA模型实现城市扩展的空间分配,实现模型的优势互补。并对比3种指标权重赋值模型,包括层次分析模型(AHP)、逻辑回归模型(LR)和二者相结合的权重赋值模型模拟结果,结果显示,整合指标权重系数方法比单一指标权重系数方法预测精度高。
1 基于整合指标权重的CA-Markov城市扩展模型
本文基于4期城市建成区扩展数据,借助Markov模型计算并分析城市建成区扩展变化规律,利用多准则判断模型(multi-criteria evaluation,MCE)将城市建成区扩展影响因素按照指标赋值法分别赋予权重,再进行整合,然后进行元胞转换规则的制定,用以集成元胞转移适宜性图集,利用元胞(CA)领域尺度下的城市建成区扩展变化潜力矩阵,对研究区域的城市建成区格局进行演化模拟。在构成适宜性图集时引入融合权重赋值法(整合AHP和LR模型)对MCE模型进行改进,再与单一指标赋值法(AHP、LR模型)演化模拟城市建成区扩展进行对比分析。最后利用点对点验证、统计城市面积验证及Kappa系数验证3种方法对模型模拟结果进行精度检验。基于整合的元胞自动机模型的城市建成区扩展变化模拟研究框架如图1所示。
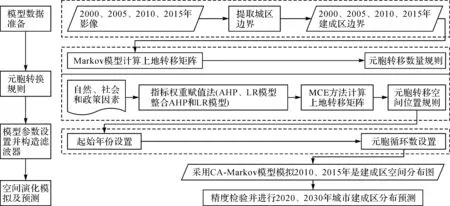
图1 基于AHP、LR与整合AHP和LR模型的CA-Markov模型的城市扩展模拟
1.1 多准则评价方法(MCE)
多准则评价方法(MCE)是在土地本身的不同的转换规则基础上评估一系列方案和决策中最优决策方案的分析方法,是一种重要的分析决策理论[21],最基本的问题是衡量每个单因素对城市建成区的相对重要性和实现标准单因素的整合。本文采用3种指标权重赋值模型(AHP模型、LR模型和AHP与LR结合模型)衡量每个单因素对城市建成区的重要程度,它对城市建成区转化具有十分重要的作用[22]。
该方法在IDRISI环境下,通过模糊集标准化后的影响因素即对每个影响因素范围在0~255栅格单元赋权重,最终构建适宜性图层(LSM),即元胞的转换规则。集成的土地适宜性图集(LSM)的MCE方法计算公式为
(1)
式中,Wi表示对城市第i类非限制性适宜条件的权重,本文利用成对比较矩阵AHP和逻辑回归矩阵LR和整合AHP和LR模型;Xi表示对城市第i类非限制性适宜条件的评分;Ci表示对第i类城市限制因子的评分,该评分范围在{0,1}。MCE值越高,土地的适宜性越好。
1.1.1基于AHP的指标权重模型
AHP是依赖于多尺度决策模型,用于检测复杂的技术、经济、社会政治问题。Tian等[23]利用AHP解释理论过程如下:①它是确定每列中主要因素和次要因素成对比较矩阵的总和的理论。②将比较矩阵中的每个元素除以其列之和(所得矩阵表示为标准化成对比较矩阵。)③计算每一行的标准得分的平均值(例如除以每行驱动因素的归一化值之和)。④利用AHP模型计算影响因素权重,其中,本文参考Tian等[24]解释的AHP模型衡量一致性比率CR结果如下
(2)
(3)
式中,CI表示一致性指标;λmax表示矩阵的最大特征值;随机指数RI是一致性平均值指数,它的值取决于矩阵的顺序。Sakieh等[13]等一些专业人士认为相对权重层CR设置应该小于等于0.1。
1.1.2基于整合的LR模型和AHP指标权重模型
利用AHP和LR模型组合赋权法即加权线性组合赋权方法,是定量化的LR模型和定性化的AHP模型的结合,弥补单一模型权重赋值方面的不足,其中根据AHP模型所确定的权重向量为
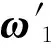
(4)
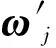
根据LR模型所确定的权重向量为
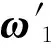
(5)
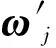
结合二者,组合权重表示为
(6)
式中,α,β≥0,且α+β=1。
当决策者对不同赋权方法存在偏好时,α能够根据决策者的偏好信息来确定。本文选取α=0.5,β=0.5。
1.2 CA-Markov模型及城市扩展模拟
1.2.1CA-Markov模型
本文采用CA-Markov模型预测城市建成区扩展。利用公式计算城市转移概率,计算公式为
S(t+1)=Pij×S(t)
(7)
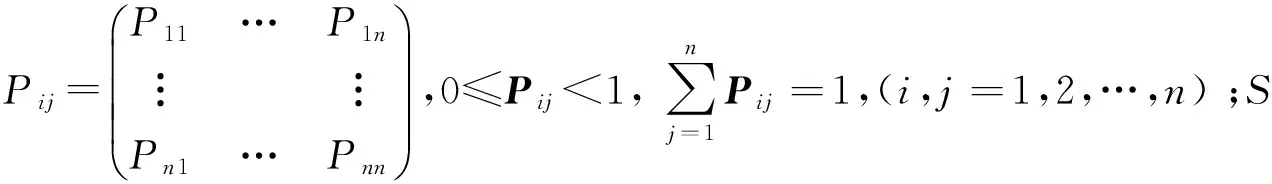
1.2.2确定起始时刻和CA循环次数
本文首先验证模型的有效性,然后预测2020、2030年建成区扩展。具体为:①计算2000—2010年、2000—2005年的城市建成区转移概率,起始年份都是2000年,CA循环次数分别为10和5,模拟2015、2010年城市建成区扩展,然后利用预测的城市建成区边界与真实城市建成区边界点对点进行对比,校准和验证模型的一致性及有效性;②计算2000—2015年、2010—2015年转移概率,分别以2000、2010年为起始年份,CA循环次数为15和5,预测2020、2030年城市建成区扩展。
2 模型应用
本节主要介绍研究区及研究数据和预测模型转换规则的应用。
2.1 研究区
本文选取云南省大理市为研究区如图2所示。大理市位于横断山西南端,滇东高原和滇西峡谷的交界地带,以山地、平坝、河谷3种地形为主,地貌复杂多样,大体可以概括为三面环山,一面环水。高山海拔在2500~3000 m之间。有国家级自然保护区苍山洱海自然保护区和市级蝴蝶泉自然保护区,大理市被评为第一批国家新型城镇化综合试点地区并建立生态园林,开发澜沧江开放经济带。城市扩展模拟是解决快速发展带来的经济和生态问题的重要手段。
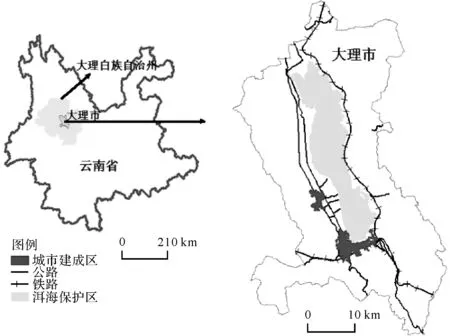
图2 研究区地理位置
2.2 基于城市建成区扩展的适宜性评价
利用多准则判断模型(multi-criteria evaluation,MCE)将城市建成区扩展影响因素按照指标赋值法分别赋予权重,再进行整合,然后进行元胞数组转换规则的制定,用以集成元胞转移适宜性图集。
2.2.1城市建成区适宜性评价及指标权重对比
元胞的转换规则是城市适宜条件和约束性条件。首先进行投影转换,统一获得UTM投影,然后借助ArcGIS空间分析功能对数据进行欧氏距离计算分析,并统一成30 m×30 m栅格;再依据以往经验,参考专家意见,根据生态环境与土地利用结构的关系,通过分析土地适宜性,把每个影像因素在ArcGIS中重分级。
本文利用AHP模型、LR模型和整合AHP和LR模型计算驱动力权重,评估单因素对城市建成区的相对重要程度,见表1。
2.2.2城市建成区扩展适宜性图集
基于LR模型、AHP模型和整合AHP与LR的模型生成的最适宜区主要分布于DEM 1800 m以下,地貌类型为平原或台地,年平均降雨1000 mm以上,距离主要公路2000 m以内,距离主要铁路3000 m以内,距离政府在3000 m以内,坡度在15°以下,年平均气温在13.3°C和17.8°C之间,土壤侵蚀微弱以下,距离医院2000 m以内。
表1基于AHP和LR模型分别计算影响因素的标准化及权重结果
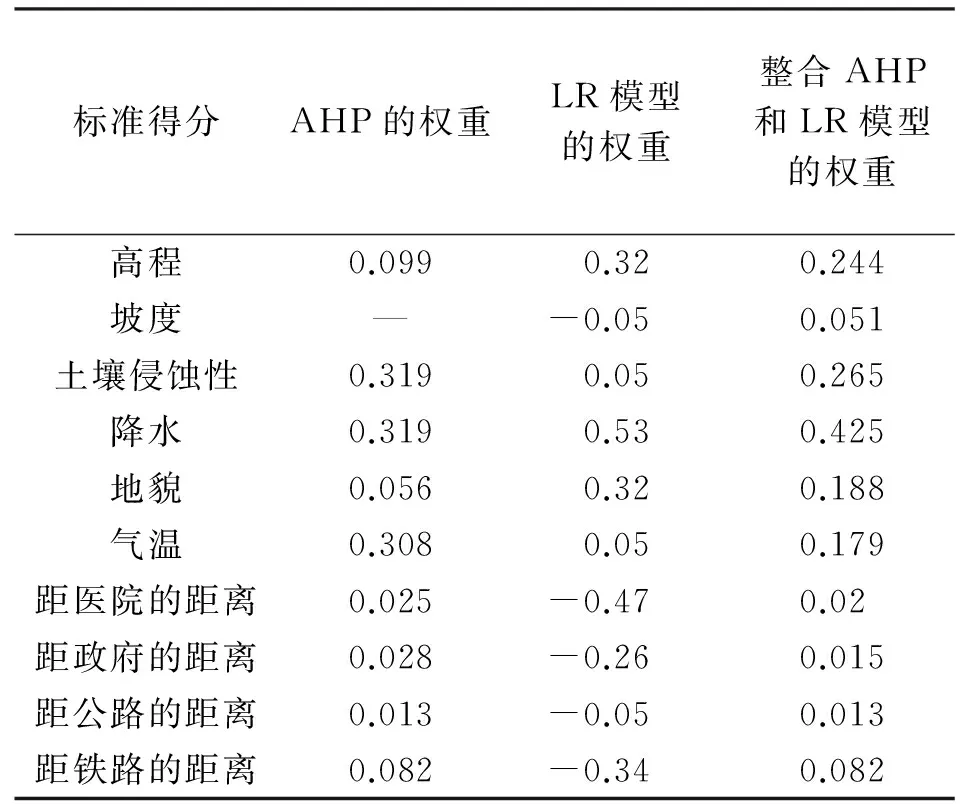
标准得分AHP的权重LR模型的权重整合AHP和LR模型的权重高程0.0990.320.244坡度—-0.050.051土壤侵蚀性0.3190.050.265降水0.3190.530.425地貌0.0560.320.188气温0.3080.050.179距医院的距离0.025-0.470.02距政府的距离0.028-0.260.015距公路的距离0.013-0.050.013距铁路的距离0.082-0.340.082
利用3种指标权重赋值模型制作出的适宜性图集有些许差别,主要表现在:①LR模型制作的适宜性图集比AHP和组合权重模型制作出的适宜性图集的最适宜区范围大,差别主要在2片建成区之间。LR模型中坡度、距离医院、政府、公路、铁路的距离影响因素为负值,但这些因素在制作适宜性图集有正面的影响,这不符合实际。②AHP模型的最适宜区面积较其他2个模型面积小,主要原因在于政策及受温度、土壤侵蚀性3种影响因素对高适宜分布区影响更大。③AHP和逻辑回归组合模型集成适宜性图集的最适宜分布区主要介于AHP指标赋值法和逻辑回归指标赋值法之间。
2.3 结果及分析
根据集成的适宜性图集的适宜性及城市建成区、非建成区之间的转移概率,整合CA模型,预测2020年和2030年城市建成区扩展,利用AHP、LR和AHP与LR的结合模型改进CA-Markov模型预测的不同建成区扩展结果如图3所示。从整体上看,3种指标权重赋值法分别预测城市建成区扩展边界形态比较一致,城市建成区用地增长依然保持开速发展趋势,在局部地区略有差别,差别在图中用圈表示,表现为:①城市建成区扩展的差别主要分布在2片建成区之间及建成区的东南和西北方向。②图(b)代表AHP方法改进的CA-Markov预测城市扩展边界向东南方向扩展较多,按照专家意见城市建成区扩展应该向这个方向扩展较多,因为在这个区域城市道路、铁路沿线发展,坡度和高程较低,适宜城市建设,但是降水较少,以山地为主,可扩展建设用地范围较小,医院和政府等基础设施不完善。③图(a)代表LR方法改进的CA-Markov预测城市建成区扩展边界主要向西北方向扩展,利用LR定量方法集成的适宜性图集中坡度、距离医院、政府、公路、铁路的距离的影响因素不符合实际,因此这几种影响因素对该地区城市建成区扩展适宜性没有参考价值。④图(c)代表整合AHP和LR改进CA-Markov预测城市建成区扩展边界介于2种模型改进方法预测的城市建成区边界范围之间,模型集成了专家知识决策(AHP)模型和逻辑回归定量化模型的优势。结果表明:指标权重模型校准预测模拟模型仍然是模型改进的关键。
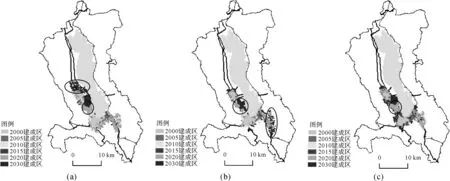
图3 2000—2030年城市扩展边界图对比
2.4 模型验证与相对精度检验结果
为了对改进模型效果进行细致分析,本文采用统计城市建成区面积对比验证及Kappa系数3种方法对模型结果进行精度检验[25]。点对点验证方法是将模拟结果与实际情况进行叠加;统计城市建成区面积对比验证方法是将城市建成区面积进行统计,比较模拟结果和实际结果的面积差值;而Kappa系数验证是评价空间模拟精度的一种常用方法,不同的Kappa系数表明相应的空间模拟一致性。Kappa系数计算结果越接近1,表明模拟结果与实际情况越接近。
(1) 采用2010、2015年城市建成区模拟结果进行验证,通过比较预测和真实建成区面积,以量化的形式进行模型精度检验,见表2。2010年预测与真实城市建成区面积相差分别为6 km2,7.31 km2,2.29 km2,结果表明整合AHP和LR模型模拟城市建成区与真实建成区面积相差最小。
(2) 基于LR的CA-Markov模型和基于AHP的CA-Markov模型和基于整合AHP和LR的CA-Markov模型的Kappa关联性分别达到了87.6%、90.6%和96.8%。同时扩展预测精度分别达到了87.85%、91.4%和97.86%。从3个模型的相关性值可以看出影响因素和城市建成区扩展有极强的相关性。
可见,整合AHP和LR模型预测城市建成区扩展可靠性高,更适用于城市建成区扩展的模拟与预测。而单一指标权重赋值模型预测城市建成区边界存在弊端,在实际生活中距离医院、政府、公路、铁路的距离影响因素对城市建成区扩展预测影响较大,但LR模型对权重进行量化,结果为负值,AHP模型对权重进行专家知识决策,符合真实情况,但不够客观。
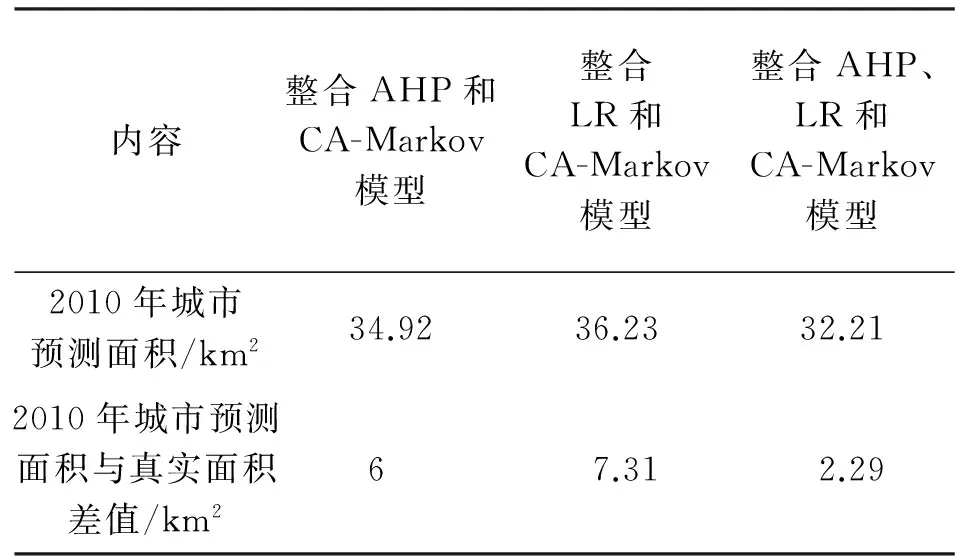
表2 2010、2015年3种模型城市真实面积及预测面积比对
3 结 语
本文研究在中国加快推进“就地就近”城镇化战略的背景下,把握小城镇城市建成区扩展变化过程及其演变机制,对制定科学合理的管控政策和优化城市空间结构具有重要意义。本文采用3种不同的指标权重改进传统CA-Markov模型,模拟复杂城市动态演变,其中,整合LR和AHP模型改进CA-Markov模型,它既满足了LR模型的定量化影响因素的优点,又继承了AHP专家知识决策,定性化的特点。采用整合指标权重模型,在状态转换规则中集成了空间约束条件、限制条件,比传统的单一赋值CA模型在模拟城市建成区扩张变化方面具有更多的优势。结果表明,CA-Markov模型及整合的指标权重方法是较为合理且有效的模拟城市建成区扩展演化的手段。然而CA的转化规则必须兼顾微观、区域和宏观,本文对于宏观GDP、人口等影响因子的分析不足,因此加强过程及微观行为的解析,并增加宏观方面的规则判断,是未来重点研究的方向。
本文研究采用点对点验证、城市面积对比、Kappa系数3种方法检验模型精度,结果证明,整合的AHP和LR改进CA-Markov模型避免了主观和客观单独操作的不足,模拟精度较高。但是对于更为普遍的研究区域是否具有相同的适用性值得进一步探讨。
参考文献:
[1] BATTY M,XIE Y,SUN Z.Modeling Urban Dynamics Through GIS-based Cellular Automata[J].Computers,Environment and Urban Systems,1999,23(3):205-233.
[2] 徐新良,赵美艳,闵稀碧.城市扩展研究的主要进展与展望[J].生态科学,2014,33(3):619-624.
[3] 陆大道.我国的城市化进程与空间扩张[J].城市规划学刊,2007(3):16-22.
[4] 刘纪远,邓祥征.LUCC时空过程研究的方法进展[J].科学通报,2009,54(21):3251-3258.
[5] 周成虎,欧阳,马廷,等.地理系统模拟的CA模型理论探讨[J].地理科学进展,2009(6):833-838.
[6] 王海军,夏畅,张安琪,等.基于约束性CA的大都市郊区城镇增长的情景模拟与管控——以武汉市江夏区为例[J].地理科学进展,2016(7):793-805.
[7] COUCLELIS H M.Cellular Worlds:A Framework for Modeling Micro-Macro Dynamics[J].Environment and Planning A,1985,17(5):585-596.
[8] 张显峰,崔伟宏.集成GIS和细胞自动机模型进行地理时空过程模拟与预测的新方法[J].测绘学报,2001(2):148-155.
[9] 杨俊,解鹏,席建超,等.基于元胞自动机模型的土地利用变化模拟——以大连经济技术开发区为例[J].地理学报,2015(3):461-475.
[10]SAATY T L.A Scaling Method for Priorities in Hierarc-hical Structures[J].Journal of Mathematical Psychology,1977,15(3):234-281.
[11]周成虎,孙战利,谢一春.地理元胞自动机研究[M].北京:科学出版社,1999:1-163.
[12]SAKIEH Y,SALMANMAHINY A,JAFARNEZHAD J,et al.Evaluating the Strategy of Decentralized Urban Land-use Planning in a Developing Region[J].Land Use Policy,2015(48):534-551.
[13]ABURAS M M,HO Y M,RAMLIET M F,et al.Improving the Capability of an Integrated CA-Markov Model to Simulate Spatio-temporal Urban Growth Trends Using an Analytical Hierarchy Process and Frequency Ratio[J].International Journal of Applied Earth Observation and Geoinformation,2017(59):65-78.
[14]聂婷,肖荣波,王国恩,等.基于Logistic回归的CA模型改进方法——以广州市为例[J].地理研究,2010(10):1909-1919.
[15]LIAO J,TANG L,SHAO G,et al.Incorporation of Extended Neighborhood Mechanisms and Its Impact on Urban Land-use Cellular Automata Simulations[J].Environmental Modelling and Software,2016(75):163-175.
[16]MULLER M R,MIDDLETON J.A Markov Model of Land-use Change Dynamics in the Niagara Region,Ontario,Canada[J].Landscape Ecology,1994,9(2):151-157.
[17]井云清,张飞,张月.基于CA-Markov模型的艾比湖湿地自然保护区土地利用/覆被变化及预测[J].应用生态学报,2016,27(11):3649-3658.
[18]MONDAL B,DAS D N,BHATTA B.Integrating Cellular Automata and Markov Techniques to Generate Urban Development Potential Surface:A study on Kolkata agglomeration[J].Geocarto International,2016,33(4):401-419.
[19]何丹,周璟,高伟,等.基于CA-Markov模型的滇池流域土地利用变化动态模拟研究[J].北京大学学报(自然科学版),2014,50(6):1095-1105.
[20]林坚,张禹平,李婧怡,等.2013年土地科学研究重点进展评述及2014年展望:土地利用与规划分报告[J].中国土地科学,2014,28(2):3-12.
[21]姜华,高国安,刘栋梁.多准则决策评价系统设计[J].系统工程理论与实践,2000(3):12-16.
[22]YANG X,ZHENG X,LV L.A Spatiotemporal Model of Land Use Change Based on Ant Colony Optimization,Markov chain and cellular automata[J].Ecological Modelling,2012(233):11-19.
[23]PARK S,JEON S,KIM S,et al.Prediction and Comparison of Urban Growth by Land Suitability Index Mapping Using GIS and RS in South Korea[J].Landscape and Urban Planning,2011,99(2):104-114.
[24]TIAN G,MA B,XU X,et al.Simulation of Urban Expansion and Encroachment Using Cellular Automata and Multi-agent System Model—A Case Study of Tianjin Metropolitan Region,China[J].Ecological Indicators,2016,70:439-450.
[25]黎夏,叶嘉安.约束性单元自动演化CA模型及可持续城市发展形态的模拟[J].地理学报,1999,54(4):289-298.

