追根溯源凸显创新
——对2018 年高考物理计算题的预测
■江苏省六合高级中学
一、回眸2017年高考
2017年高考物理命题坚持立德树人,突出高考的思想性和育人功能,引导物理核心素养的培养,深化考试内容的改革,落实物理考试大纲修订的考核要求。试卷在突出基础性、注重综合性、加强应用性、凸显创新性等方面做出了积极的探索,并采取精准调整策略,合理控制试卷难度,以适应不同层次水平的考生实际。
其中2017年高考全国Ⅰ卷的计算题具有如下特点:第24题是一道常规得不能再常规的试题,较容易得分,但由于计算量较大,很多考生会有“算得生无可恋”的感觉。第25题的难度较高,命题者要求从牛顿第二定律出发,结合匀变速直线运动规律与电场解决第一问,而第二问的设计很有意思,虽然从电场出发,但和电势能几乎没有关系,是一道比较纯粹的运动学问题,考生只需分情况讨论即可。也可能综合匀变速直线运动规律考查。命题特点倾向于应用型、综合型和能力型,命题情境将密切联系航天科技、体育、生活等。同学们在解决此类问题时要将所学物理知识与实际情境联系起来,抓住问题实质,将问题转换为熟知的物理模型进行求解。

图1
例1 将一根长为l的光滑细钢丝ABCDE制成如图1所示的形状,并固定在竖直平面内。其中AD段竖直,DE段为圆弧,圆心为O,E为圆弧的最高点,C与E、D与O分别等高,。将质量为m的小珠套在钢丝上由静止释放,不计空气阻力,重力加速度为g。
(1)若小珠由B点释放,从E点滑出后恰好撞到D点,求圆弧的半径R。
(2)若小珠由A点释放,求它到达E点时的速度大小和对轨道的压力大小。
(3)欲使小珠到达E点时与钢丝间的弹力超过,求释放小珠的位置范围。
二、展望2018年高考
首先,两道计算题的难度都较大,其中第一道计算题的情境常规但计算量较大,预测2018年高考试题涉及天体和机械能综合问题是大概率事件,且对考生的数学运算能力要求高,因此同学们在平时的做题过程中,要多动手算,谨记少拿计算器,不能望题却步;其次,2017年高考的考查热点值得高度重视和深入研究;最后,带电体在电场或磁场中的运动依然是命题的重点和热点,而从综合分析角度来预测2018年高考考查电磁感应的综合运用应该是大概率事件,值得拭目以待。
考向一:牛顿运动定律和功能关系
牛顿运动定律和功能关系是高中物理的核心和基础,是解决力学问题的重要途径,每年高考试题中均有体现,两者可能单独考查,
追根溯源:本题涉及的核心考点有牛顿第二定律、平抛运动、圆周运动、动能定理等。试题以竖直平面内的细钢丝构建成的两个不同轨道为背景,对该问题情景进行模型化处理,即可围绕着自由落体运动、圆周运动、平抛运动等设计问题,物理过程清晰而又熟悉,同时又综合考查了应用数学方法对实际问题的分析与讨论。
解析:(1)由题意可知,B、E两点的高度差,小珠在由B点运动到E点的过程中,由动能定理得mgh=。小珠从E点滑出后恰好撞到D点,
(2)小珠在由A点运动到E点的过程中,由动能定理得,将代入上式解得。根据牛顿第二定律得小珠到达E点时轨道对它的弹力满足关系式N+mg=,解得N=mg。根据牛顿第三定律得小珠对轨道的压力大小为mg。
(3)若小珠到达E点时,小珠受到的钢丝对它的弹力向下,且等于mg,则N1+小珠在从释放点运动到E点的过程中,由动能定理得,解得若小珠到达E点时,小珠受到的钢丝对它的弹力向上,且等于mg,则小球在从释放点运动到E点的过程中,由动能定理得解得因此当小珠从C点上方低于处或高于处滑下时,小珠到达E点时与钢丝间的弹力将超过
方法点拨:本题综合了平抛运动和圆周运动两个运动形式,明确平抛运动在竖直方向和水平方向上的运动规律,以及小珠做圆周运动所需向心力的来源,并结合牛顿第二、第三定律和动能定理即可求解。
例2 如图2所示,竖直光滑半圆形轨道CDE与水平粗糙轨道ABC相切于C点,轨道的AB部分可绕B点转动,一质量为m的滑块(可视为质点)在水平外力F的作用下从A点由静止开始做匀加速直线运动,待滑块运动到B点时撤去外力F,滑块恰好能够通过最高点E。现将轨道AB沿顺时针方向转过37°,若将滑块从A点由静止释放,则滑块恰好能够到达与圆心等高的D点(不计滑块在B点的能量损失)。已知滑块与轨道ABC间的动摩擦因数μ=0.5,重力加速度为g,sin37°=0.6,。求:

图2
(1)水平外力F与滑块重力mg大小的比值。
(2)若轨道AB光滑,其他条件不变,滑块仍从A点由静止释放,求滑块在E点处对轨道的压力大小。
追根溯源:本题涉及的核心考点有牛顿第二定律、圆周运动、动能定理。求解单物体多过程运动问题时往往需要利用牛顿运动定律和动能定理综合分析。选取合适的运动过程,并尤其关注物体运动过程和运动状态的一一对应关系,利用动能定理计算摩擦力做功,正确判断滑块在竖直面内做圆周运动的临界条件。
解析:(1)滑块恰好能通过最高点E,则设轨道AB的长度为x,则滑块在从A点运动到E点的过程中,由动能定理得将轨道AB沿顺时针方向转过37°,滑块在从A点运动到恰好到达D点的过程中,由动能定理得,解得因此水平外力F与滑块重力mg大小的比值
(2)若轨道AB光滑,其他条件不变,滑块仍从A点由静止释放,设滑块运动到E点的速度v,则在滑块从A点运动到E点的过程中,由动能定理得设在E点轨道对滑块的弹力为N,则由牛顿第二定律得N+mg=解得N=2mg。根据牛顿第三定律得滑块对轨道的压力大小为2mg。
方法点拨:求解本题需要先明确滑块的运动情况,再分过程运用动能定理、牛顿第二定律和圆周运动的临界条件列式求解。本题的物理情景明晰,物理模型常规,突出考查物理主干知识的理解和应用能力,难度适中。
考向二:带电体在电场中的运动
分析近三年的高考试题我们可以发现,考查带电体在重力场、电场和磁场组成的复合场中的运动的频率和热度都有所降低。然而带电体在电场中的运动历年来是高考试题的“常客”,且多以选择题的形式考查静电力与能的性质,也常以计算题的形式考查带电体做类平抛运动、匀变速直线运动等。
例3 在如图3所示的绝缘水平面上,有两个边长d=0.2m的正方形区域Ⅰ、Ⅱ,其中区域Ⅰ中存在水平向右、场强E1=30N/C的匀强电场(图中未画出),区域Ⅱ中存在竖直向上、场强E2=150N/C的匀强电场(图中未画出)。现有一可被视为质点的质量m=0.3kg的滑块以速度v0=1m/s由区域Ⅰ边界上的A点进入电场,经过一段时间滑块从边界上的D点离开电场(D点未画出),滑块带有电荷量q=+0.1C,滑块与水平面间的动摩擦因数μ=0.75,取g=10m/s2。
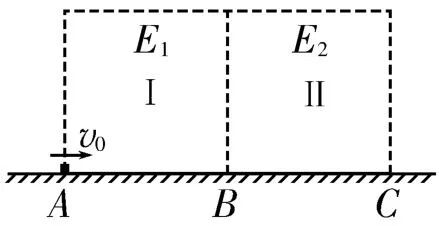
图3
(1)D点与A点的水平间距、竖直间距分别为多少?
(2)滑块在D点的速度为多大?
(3)若仅改变区域Ⅱ中场强的大小,欲使滑块从区域Ⅱ中的右边界离开电场,则区域Ⅱ中的场强大小的取值范围应为多大?
追根溯源:本题涉及的核心考点有匀变速直线运动规律、牛顿第二定律、平抛运动、动能定理。带电体在电场中运动常有下列两种情况:一是带电体沿与电场线平行的方向进入匀强电场,受到的静电力与运动方向在同一直线上,做加速(减速)直线运动,此时常用匀变速直线运动规律、牛顿运动定律和功能关系来分析求解;二是带电体以垂直于电场线方向的初速度进入匀强电场,做匀变速曲线运动(类平抛运动),此时应用运动的合成与分解来分析,即在垂直于电场线方向上的分运动为匀速直线运动,在平行于电场方向上的分运动为做初速度为零的匀加速直线运动。
解析:(1)滑块在区域Ⅰ中运动时,根据牛顿第二定律得qE1-μmg=ma1,解得a1=2.5m/s2。设滑块运动到两电场区域的交界点B时的速度为vB,则v2B-v20=2a1d,解得vB=2m/s。滑块在区域Ⅱ中做类平抛运动时,根据牛顿第二定律得qE2-mg=ma2,解得a2=40m/s2。假设滑块从区域Ⅱ的上边界离开电场,运动的时间为t0,则根据类平抛运动的规律可知,滑块在水平方向上做匀速直线运动,在竖直方向上做匀加速直线运动,则,解得d,因此该假设成立。所以D点与A点的水平间距,D点与A点的竖直间距yDA=d=0.2m。
(2)设滑块在D点的速度为vD,则对滑块的整个运动过程应用动能定理得qE1d-,解得
(3)滑块在区域Ⅱ中运动,刚好从右边界的最上端离开时,根据类平抛运动规律可知,在水平方向上有d=vBt,在竖直方向上有,解得a3=20m/s2。根据牛顿第二定律得qE3-mg=ma3,解得E3=90N/C。若滑块到达C点时的速度刚好为0,由匀变速直线运动规律得2a4d=v2B,解得a4=5m/s2。根据牛顿第二定律得μ(mgqE4)=ma4,解得E4=10N/C。因此欲使滑块从区域Ⅱ中的右边界离开电场,则区域Ⅱ中的电场强度大小的取值范围应为10N/C<E≤90N/C。
方法点拨:本题以带电体在电场中的受力为背景,考查带电体的多过程运动——匀变速直线运动和类平抛运动,涉及电场和重力场的叠加。
考向三:电磁感应与其他知识的综合
历年高考对电磁感应部分内容的考查常见的是给定情境下感应电流和感应电动势的分析计算,其中对感应电流(感应电动势)随时间变化的考查常以图像的形式出现,另外,电磁感应现象与运动学、牛顿运动定律、功能关系、电磁学等知识相联系的综合问题是近几年高考考查的热点问题之一。

图4
例4 如图4所示,两根金属导体棒c和d的长度均为L,电阻均为R,质量分布均匀且大小分别为3m和m,现用两根等长的、质量和电阻均可忽略不计且不可伸长的柔软导线将它们连成闭合回路,并悬跨在光滑绝缘的水平圆棒两侧。其中导体棒d处在宽度为H、垂直于纸面向里、磁感应强度为B的匀强磁场中,导体棒c在磁场的正上方。现将导体棒d从磁场的下边界由静止释放,若磁场宽度H足够大,导体棒d在穿过磁场的过程中,导体棒c未能进入磁场,在整个运动过程中导体棒c、d始终处于水平状态,重力加速度为g。求:
(1)导体棒d在磁场中运动时能获得的最大速度vmax。
(2)若导体棒d获得最大速度v时,恰好达到磁场的上边界,则导体棒d从释放到穿出磁场所需要的时间t。
(3)在(2)问过程中产生的热量Q。
追根溯源:本题涉及的核心考点有牛顿第二定律、法拉第电磁感应定律和能量的转化与守恒定律。导体棒d在重力、导线的拉力和安培力的作用下做变速直线运动,需要考生先通过对导体棒受力情况的具体分析弄清物理状态和物理过程,建立导体棒运动的物理图像,再综合应用牛顿第二定律、法拉第电磁感应定律和能量的转化与守恒定律等知识列式,然后利用数学方法解决相关问题。
解析:(1)设导线的拉力大小为T,导体棒d受到的安培力为F安,根据牛顿第二定律对导体棒c有3mg-2T=3ma,对导体棒d有2T-mg-F安=ma,整理得2mg-F安=4ma。导体棒d切割磁感线产生的感应电动势E=BLv,感应电流,因此F安=当导体棒d的速度最大时a=0,解得
(2)由(1)可知,导体棒d在上升过程中的加速度,由微元法得,解得
(3)在(2)问过程中以由导体棒c、d组成的系统为研究对象,由能量的转化与守恒定律得,解得
方法点拨:本题综合考查牛顿第二定律、法拉第电磁感应定律、能量的转化与守恒定律等主干知识点的理解和核心考点的综合应用。尤其突出考查应用微元法处理物理问题的数学运用能力,属于较难题。

