理解矢量特点 掌握运算法则——探析力的合成与分解学习策略

■浙江省义乌市第二中学　

一、一个法则

力的合成与分解的根本方法:矢量的运算法则——平行四边形定则。平行四边形定则就是以表示两个共点力的有向线段为邻边作一平行四边形,该两邻边之间的对角线即表示两个力的合力的大小和方向。两个确定的分力,它们的合力是唯一确定的;一个合力(确定的对角线),在没有其他条件限制时,可作的平行四边形有无限多个,即有无限多种分解方法。

二、两个规律

1.力的合成规律。

如图1所示,当两个共点力F1和F2间的夹角为θ时,利用数学知识可以求得合力F的大小和方向。合力F的大小为合力F与F1间的夹角α满足tanα=

图1

(1)当F1和F2同向,即夹角θ=0°时,它们的合力最大,其大小F=F1+F2,方向与两个力的方向相同。

(2)当F1和F2反向,即夹角θ=180°时,它们的合力最小,其大小F=|F1-F2|,方向与F1和F2中较大的力同向。

(3)当F1和F2互相垂直,即夹角θ=90°时,它们合力的大小且合力F与F1间的夹角α满足

设计意图：通过视频，吸引学生的有意注意，使学生体验生物分类的重要意义。这样，学生学习到了生活常识，增强学习的自信心，从而引入了新课。

(4)当F1和F2的大小相等且它们间的夹角θ=120°时,这两个力的合力大小与F1或F2大小相等,合力F与F1、F2间的夹角均为60°。

2.力的分解规律。

在力的分解中,把一个已知力分解为两个分力,就相当于已知平行四边形的对角线,此时能作出多少个平行四边形,这个力就可以分解为多少对大小、方向不同的分力。因此,在力的分解中,必然涉及合力的大小和方向、两个分力的大小和方向等六个因素,当涉及的因素越多,即限制的条件越多时,其分力的对数就越少。

(1)当力的分解涉及四个因素时:①已知合力的大小和方向、两个分力的方向时,只有唯一解。②已知合力的大小和方向、一个分力的大小和方向时,只有唯一解。③已知合力的方向、一个分力的大小和方向,以及另一个分力的方向时,只有唯一解。④已知合力的大小和方向、两个分力的大小。当F=F1+F2时,只有一组解;当F＜F1+F2时,有两组解;当F＞F1+F2时,无解。⑤已知合力F的大小和方向、一个分力F1的方向及另一个分力F2的大小时,作出F1、F2和F的矢量三角形图,如图2所示,则由于合力F和分力F2的大小关系不同,存在四种情况。Ⅰ.当F2＜Fsinθ时,无 解;Ⅱ.当F2=Fsinθ时,有唯一解;Ⅲ.当Fsinθ＜F2＜F时,有两个解;Ⅳ.当F＜F2时,有唯一解。

图2

(2)当力的分解涉及三个因素时:①已知合力F的大小和方向、一个分力F1的方向时,有无数组解,但另一个分力F2的大小有范围限制,即F2≥Fsinθ。②已知一个分力F1的大小和方向、合力F的方向时,有无数组解,但另一个分力的大小也有范围限制,即F2≥Fsinθ。

(3)当力的分解涉及两个因素时:已知合力的大小和方向,其他因素无限制时,将有无数组解。

在力的分解时,必须按照力作用的实际效果进行分解,从而确定两个分力的方向,再根据平行四边形定则作出力的分解图,最后利用数学知识求出两个分力。

例1如图3所示为一曲柄压榨机的示意图,其中O为固定铰链,杆OA与AB等长。在压榨机铰链A处作用的水平力为F,OB是铅垂线。如果杆和活塞的重力忽略不计,在已知角α的情况下,求活塞作用在物体M上的压力。

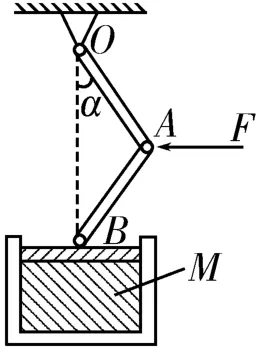
图3

分析:力F的实际作用效果是对AB、AO两杆沿杆方向产生挤压作用,因此可将力F沿AB、AO方向分解为FAB、FAO,如图4甲所示,由几何关系得力FAB的实际作用效果是对活塞有水平向左和竖直向下的挤压作用,因此可将力FAB沿水平方向和竖直方向分解为Fx和Fy,如图4乙所示,由几何关系得因为活塞的重力不计,所以活塞对物体M竖直向下的压力大小

图4

三、六种相互关系

合力与分力是一种等效替代关系,因此同学们必须深刻理解以下六个关系。

(1)效果相同。如果一个力产生的效果与某几个力产生的效果相同,那么这个力就叫那几个力的合力,而那几个力就叫这个力的分力。合力的作用效果与分力共同作用的效果一定相同。

(2)等效替代。合力与分力之间是一种等效替代关系,且这种等效替代关系是可逆的,即有时可以用一个力(合力)来代替某几个力(分力),而有时也可以用几个力(分力)来代替某一个力(合力),代替前后的作用效果相同。

(3)遵守法则。求几个力的合力的过程叫力的合成,求一个力的分力的过程叫力的分解。力的合成与分解遵循力的平行四边形定则。当求两个以上的力的合力时,可以先求出任意两个力的合力,再求出这个合力与第三个力的合力,依此类推,直至求出所有的力的合力为止。

(4)大小关系。合力可能大于任何一个分力,也可能小于任何一个分力,也可能介于两个分力之间。当两个分力F1、F2的夹角θ在0°到180°之间变化时,其合力F的大小变化范围是|F1-F2|≤F≤F1+F2。

(5)相同性质。一个分力和产生这个分力的合力是同性质的力,且产生于同一个施力物体。

(6)存在关系。在进行物体的受力分析时,合力和分力不能并存。

例2 在医院里常用如图5所示装置对小腿受伤的病人进行牵引治疗,不计滑轮组的摩擦和绳子的质量,绳子下端所挂重物的质量m=5kg,ab段绳子与水平方向间的夹角θ=30°,g取10N/kg。问:

图5

(1)病人的脚所受水平方向的牵引力是多大?

(2)病人的脚和腿所受竖直向上的牵引力共是多大?

分析:(1)因为绳子中各处与其他物体没有结点,所以绳子中各处的张力都等于所悬挂的重物的重力,即F=mg=50N。将ab段绳子的拉力沿水平方向和竖直方向分解,如图6所示。在水平方向上有Fx=Fcos30°=43.3N,在竖直方向上有Fy=Fsinθ=25N,所以病人的脚所受水平方向的牵引力F牵=F+Fx=93.3N。

图6

(2)病人的脚和腿所受竖直向上的牵引力F牵'=F+Fy=75N。

点评:力的合成与分解知识与实际生活中的许多问题紧密相连,求解此类问题时,首先要明确研究对象的受力情况,再根据实际情况进行力的合成与分解。

跟踪训练

1.如图7所示,用一根长为l的细绳一端固定在O点,另一端悬挂质量为m的小球A,为使细绳与竖直方向间的夹角θ=30°且绷紧,小球A处于静止,求对小球施加的最小的力。

图7

2.如图8所示,放置于水平地面的三脚架上固定着一质量为m的照相机。三脚架的三根轻质支架等长,与竖直方向均成30°角,求每根支架中承受的压力大小。

图8

参考答案:1