一种基于改进遗传算法的唯相波束形成方法

刘 豪 ，赵璐璐 ，梁 广 ，余金培

（1.中科院上海微系统与信息技术研究所上海200050；2.上海微小卫星工程中心上海201203）

在卫星或雷达通信中，由于发射方和接收方的距离较远，杂波干扰较大，所以对天线低副瓣要求极高。倘若对阵元的激励电流不作处理，则阵列方向图第一旁瓣高度理论值约为-13.4 dB，达不到雷达天线对旁瓣的要求。经典的旁瓣压制方法有切比雪夫加权法、泰勒综合法等，这些方法虽然有着很好的抑制旁瓣的效果，但都是幅度加权，在实际工程中大大增加了馈电网络的复杂性，不利于工程实现。而唯相波束形成仅需改变阵元的相位权值便可对旁瓣有一定的抑制，工程实现时仅需移相器即可。

然而，唯相位加权实现低副瓣问题在数学上属于非线性优化问题，目前还未取得相应的解析解，这给研究工作带来了很大的困难。文献[3]采用最速下降法（SDM）来降低线阵旁瓣高度，这种解析方法受阵列本身影响较大，分析和计算复杂。文献[4]采用相位扰动法来降低阵列旁瓣，该方法有一定的遗传算法思想，但易陷入局部最优。文中对传统GA基本步骤中的初始种群生成、交叉操作和变异操作进行了改进，提出了一种改进的遗传算法。该算法有一定的自适应思想，能够提高GA的收敛速度和跳出局部最优达到全局最优，从而获得更低的旁瓣，基于改进算法的唯相波束形成有着较优的性能[6]。

1 相位控制阵列模型分析

1.1 线阵波束形成模型

以线阵为例，假设阵列是由N个全向阵元组成的均匀线阵，期望信号为窄带信号且信号入射方向角为θ，阵元间距为d，入射信号波长为λ，且满足d=λ/2，假设第n个阵元的权值即相移常量为φn，在忽略阵元间互耦影响的条件下，该线阵的方向图函数为：

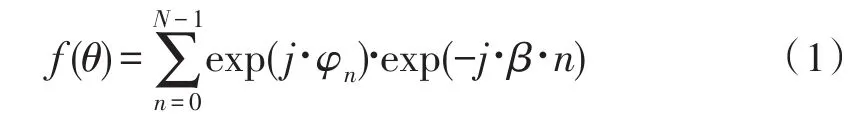
由式（2）可知，阵元间距d取0.5λ，则当θ=0°时，F（θ）取最大值，此时信号得到同向相加，能得到最佳接收。通过调整阵元的相位权值系数φn，可改变阵列方向图主瓣指向和旁瓣高度，后面将运用改进的遗传算法来求得最佳的相位权值φn，使主瓣指向目标方向且旁瓣高度最低。

1.2 面阵波束形成模型

假设均匀面阵各阵元完全相同，坐标原点是阵列的一个端点，在x方向和y方向阵元间距分别为dx、dy，且x方向M个阵元，y方向N个阵元。θ，φ分别代表方位角和俯仰角，如图1所示。

图1 平面阵列模型

由于本文仅研究相位控制阵列，仅改变阵元的相位权值，所以假设阵元的初始相位权值为φm，n。则阵列方向图为：

式中u=sinθcosφ，v=sinθsinφ，kc=2π/λ为自由空间波数。改变φm，n来调整主瓣指向且使旁瓣高度最低。

2 传统遗传算法在波束形成中的应用

遗传算法（Genetic Algorithm，GA）是一种在全局范围内的概率搜索方法，即通过某种特定的方法在自变量的全局范围内找出一组解使目标函数最优。GA基本原理效仿了生物界中的物竞天择、适者生存的进化法则，通过把待优化的参数编码成染色体，再循环进行选择、交叉、变异等操作直至种群的最优解达到目标函数要求或迭代次数达到设定值，从而生成符合目标函数要求的最优解。GA算法的主要步骤如下：

1）编 码

采用实数编码，将阵元的相位依次排列成一个矢量构成染色体，如N个阵元的阵列可编码为φ=[φ1,φ2,…,φn]，即有N个优化变量。

2）选 择

选择操作建立在目标函数之上，根据优化的目标构造目标函数，目标函数值越大的个体适应度越高。然后通过轮盘赌的方式选择适应度较高的染色体，适应度高的染色体被选中的概率大。另外还可按照实际需要设置代沟，每次选择操作时淘汰掉一部分适应度低的染色体。

3）交 叉

要进行交叉操作首先要设置交叉概率px，再从种群中随机选择两个个体，按照交叉概率的大小来判断是否对选中的个体进行交叉操作。交叉操作可使两个优良个体的基因交换，从而产生适应度更高的优秀个体，增大了解的全局性。

4）变 异

为了保持种群中个体多样性，实现全局最优，还需对种群中部分个体进行变异操作。首先设置变异概率pm，再选择个体的一个码元按照一定的规则进行变异，也可对个体产生随机扰动变异，以产生更优秀的个体作为下一次迭代的初始种群的一部分。

总结一下GA流程图如图2所示[2]。

图2 遗传算法基本流程

阵列天线波束形成中需要优化的变量随着阵元数的增加而增多，当阵元数较多时，传统GA存在收敛速率慢，运算效率低和稳定性差等问题，往往导致达不到波束形成性能要求。GA在波束形成的应用中由于待优化变量个数多，所以容易陷入局部最优，或不能收敛到全局最优解，即全局性能较差。在仅改变相位的相控阵天线中，优化目标为阵元的相位权值，目标方向图要求旁瓣高度尽可能低，而相位改变的无规律性，对GA全局性能要求更高，此时需要对传统遗传算法进行一定的改进，实现效率最高，结果最优。

3 改进遗传算法

文中对遗传算法的改进主要集中在初始种群的选择，交叉操作的改进以及变异操作的改进上。

1）初始种群的选择

结合目标方向图的特性，运用传统的解析方法计算得到若干组权值作为遗传算法初始种群的一部分，有目标的选择初始种群，比如在优化目标为给定主瓣波束指向，旁瓣尽可能低时，此时可以把普通相控阵的相位偏移权值作为初始种群的一个个体；在优化目标为成片零点生成时，可把相应的解析解作为初始种群的个体；在多波束天线中，可把多个波束对应的权值相加作为初始种群的个体。除此之外，传统GA随机生成初始种群，这会导致变量分布不均匀，所以在改进GA中把变量所在区间分成若干份，然后在每个小区间中随机生成初始个体，这样可大大增加算法收敛于全局最优的可能性，且可以提高收敛速度。

2）交叉操作的改进

在GA中，交叉操作是其重要环节，交叉策略在很大程度上决定了算法性能的好坏。但在传统GA中，因为很多相似个体之间的繁殖，导致交叉操作效果欠好，极大的影响了收敛速率，甚至不能收敛到全局最优解。之所以会出现这种现象，其本质原因是：随着迭代次数的增加，种群进化到一定程度后会出现很多非常相似的个体，这些相似个体的相同基因很多，交叉操作难以产生新的个体，从而造成种群的封闭性。

针对以上问题，很容易想到的一个解决方法，即在两个个体进行交叉前先进行检测，若是待交叉的个体相似度很高，则不能直接进行交叉操作，需对其中一个个体进行随机扰动，然后再进行交叉操作。此方法与人类的繁殖方式类似。文献中定义了个体的相关性和种群的多样性，其过滤操作去掉了与待交叉个体不相关指数为1或者0的个体，从而避免出现无效的交叉操作。本文针对无效交叉操作的改进：1）进行亲缘关系检测，即通过比较两个个体的相似度来判断是否进行交叉，如下式：

式中，U1（i）和U2（i）分别为个体U1，U2的第i个变量，根据实际需求设置临界值δ，若d（i）小于δ，则个体U1和U2的第i个变量相似；若个体U1和U2中相似变量的比例达到了单个个体变量总数的50%以上，则U1和U2相似，不能直接交叉。2）对个体随机扰动，具体对两个个体中适应度较小的个体做一个随机扰动，然后再进行交叉。这样就增大了种群中个体的多样性，有利于跳出局部最优，到达全局最优。通过对标准GA交叉操作的改进，克服了标准GA收敛速度慢，易陷入局部最优等问题，提高了优化效率。

3）变异操作的改进

变异操作在遗传算法中属于辅助性操作，对保持种群中个体的多样性有着重要作用，若无变异操作，则搜索的结果往往很容易陷入局部最优，从而出现早熟及不收敛现象。与变异操作相关的是变异概率Pm，传统GA中，Pm取值固定不变，这样会导致如果变异概率取值过小，就不易产生新的个体；若是取值过大，那就不能保留优秀基因，从而变得毫无意义。

此外，GA在应用于阵列波束赋形等自变量较多的问题时，若变异概率取值固定不变，则会导致算法效率低下[7]。

鉴于此，本文对变异操作的改进体现在对变异概率Pm的改变上，基本思想是当种群中个体的平均适应度值较小时，采用较小的变异概率；当个体平均适应度与最优个体适应度差值较小时，采用较大的变异概率。假设每一次迭代种群中最优染色体的适应度为Fopt，种群的平均适应度为Favg，可采用双变异概率或者多变异概率。以双变异概率为例，分别为Pm1和Pm2，且Pm1＜Pm2（可假设Pm1=0.05，Pm2=0.2），当Fopt与Favg的差大于某个临界值σ时，此次迭代采用Pm1为变异概率；当Fopt与Favg的差小于临界值σ时，此次迭代采用Pm2为变异概率。如式（5）所示：

4 仿真及性能分析

4.1 线阵仿真

选择由40个全向阵元组成的均匀线阵，不考虑阵元间的耦合现象。阵元间距为d，阵元间距与入射信号波长之比d/λ=0.5。假设适应度函数为F，则优化目标函数可定义为F=MSLL，式中MSLL为最大相对旁瓣电平，计算公式为，f（θ）为阵列的方向图函数，D为方向图旁瓣区域。若主瓣指向0°且主瓣零点波束宽度为BW0（结合实际情况，此处BW0可取为6°），则旁瓣区域D可表示为D=。传统的遗传算法初始种群随机生成，交叉概率Px=0.8，变异概率Pm=0.05；改进的遗传算法中把普通相控阵天线的系数作为初始种群的一个个体，其余个体按区间随机生成，交叉操作时进行亲缘关系检测，变异操作采用双变异概率，其中Pm1=0.1，Pm2=0.2；初始种群大小设置为200，最大迭代次数200。仿真结果如图3～4所示。

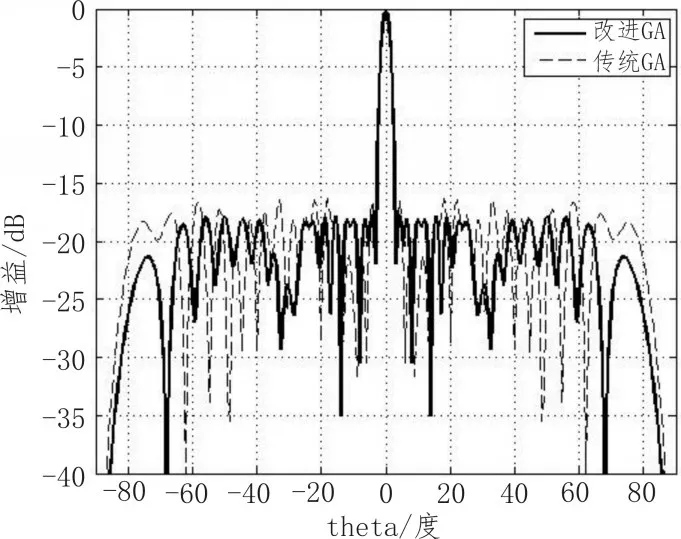
图3 波束指向角为0°方向图

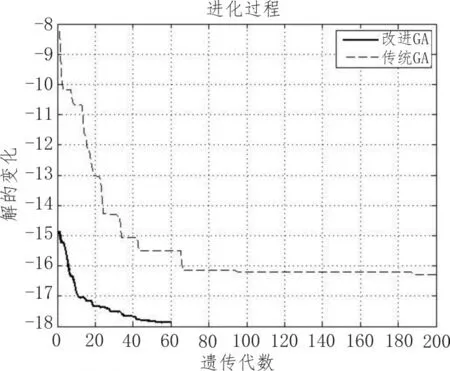
图4 进化代数比较

通过观察图3可以发现，改进的遗传算法旁瓣高度约为-17.8 dB，而传统的遗传算法获得的旁瓣高度为-16.3 dB；通过图4可见，改进的遗传算法在迭代到60左右就已收敛到最优解，而传统的遗传算法迭代到200代时还未收敛到最优解，从而验证了改进的遗传算法在相控阵天线旁瓣抑制上具有更好的全局性且能够更快的收敛到最优解。

4.2 面阵仿真

选择由64个全向阵元组成的8×8均匀面阵，不考虑阵元间的耦合现象。阵元间距为d，阵元间距与入射信号波长之比d/λ=0.5。在平面阵列中，方向图的主瓣区域应是一个圆，此时旁瓣区域D可表示为D={u,v|v2+v2≥δ2且-1≤u,v≤1} ，其中δ是跟主瓣波束宽度有关的常量。其余变量的设置与线阵仿真中的基本一致，仿真结果如图5、6所示。

图5 φ=0°剖面方向图

图6 面阵进化代数比较

观察图5和图6，改进的遗传算法能够获得较传统遗产算法更低的旁瓣，具体分别为-14.62 dB和-13.00 dB，且改进的遗传算法有更高的优化效率，即该算法能够更快速收敛到最优解，结论与线阵仿真基本一致，验证了本文提出的改进的遗传算法的正确性和有效性。

5 结束语

文中首先推导了一维均匀线阵和二维均匀平面阵列的方向图函数公式，接着分析了传统遗传算法在阵列天线波束赋形中可能存在的问题，结合遗传算法的特性阐明了“早熟”、不收敛以及算法效率低等现象产生的原因。重点提出了一种改进的遗传算法，此方法针对传统GA可能出现的问题，对GA过程中初始种群的选择，交叉操作以及变异操作进行了优化改进。通过MATLAB分别对线阵和面阵进行仿真，仿真结果表明改进GA能得到更低的旁瓣，并且算法的效率大大提高，从而验证了本文提出的改进GA在唯相波束赋形中的有效性，为以后进一步研究奠定了基础。

参考文献：

[1]张小飞，陈华伟，仇小锋，等.阵列信号处理及MATLAB实现[M].北京：电子工业出版社，2015.

[2]郁磊.MATLAB智能算法30个案例分析[M].北京：北京航空航天大学出版社，2015.

[3]韩卫国，徐超.一维线阵唯相位低副瓣技术分析[J].雷达与对抗，2013，33（1）：17-20.

[4]闫秋飞.一维唯相位低副瓣技术研究[J].舰船电子对抗，2009，32（5）：52-55.

[5]申建华，郑晓冬，赵麟．基于遗传算法的波束形成算法研究[J].无线电通信技术，2015，41（3）：83-85．

[6]张友益，徐朝阳.相位加权低副瓣阵列天线综合技术研究[J].船海电子对抗，2014，37（1）：71-77.

[7]周宇鹏张争气.基于改进遗传算法的波束形成方法[J]，计算机仿真，2010，27（8）：208-211.

[8]单俊涛，尹武，周继宇.一种改进的自适应波束赋形算法[J].广东通信技术，2012，32（1）：36-38.

[9]孙冬暖.阵列天线的方向图综合研究与分析[D].西安：西安电子科技大学，2014.

[10]马晓峰，冯丹萍，吴玉清，等.一种星载阵列天线的高效波束赋形算法[J].电波科学学报，2016，31（3）：479-485.

[11]S Jayaprakasam，SKA Rahim，LC Yen KR Ramana⁃than.Genetic Algorithm BasedWeight Optimization for Minimizing Sidelobes in Distributed Random Array Beamforming[J].International Conferenceon Parallel&Distributed Systems，2013：623-627.

[12]张海生，于勇，师亚辉，等.基于改进遗传算法的子阵级数字波束形成方法[J].遥测遥控，2016，37（4）：1-6.

[13]伍麟珺.改进遗传算法在线阵波束方向图中的应用[J].电子世界，2012（3）：22-25.

[14]H Pessentheine，G Kubin，H Romsdorfer.Improving Beamforming for Distant Speech Recognitionin Re⁃verberant Environments Using a Genetic Algorithm for Planar Array Synthesis.Speech Communica⁃tion；10 Itg Symposium，2012，58（3）：1-4.

[15]周媛.相控阵天线子阵级波束形成及优化[D].西安：西安电子科技大学，2014.

[16]尚勇.星载多波束相控阵天线综合优化技术研究[D].上海：中国科学院上海微系统与信息技术研究所，2012.

[17]丛友记，卞美琴，简玲，等.一种唯相位加权降低天线副瓣技术研究[J].雷达与对抗，2015，35（2）：45-48.