基于数据挖掘的建筑工程造价成本预估模型

樊文广

摘 要： 成本预估是建筑工程管理中的一个重要研究方向，传统模型无法精准描述建筑工程造价的变化趋势，导致建筑工程造价成本预估精度低，为此，设计了基于数据挖掘的建筑工程造价成本预估模型。建立建筑工程造价成本预估的数学模型，采用最小二乘支持向量机对建筑工程造价成本预估数学模型进行求解，并采用改进粒子群算法对模型再优化，通过具体建筑工程造价成本预估实验对有效性进行验证，数据挖掘提高了建筑工程造价成本预估的精度，且建筑工程造价成本预估性能要优于当前其他建筑工程造价成本预估模型。

关键词： 建筑工程； 质量管理； 成本预估； 数据挖掘； 数学模型； 工程造价

中图分类号： TN911.1?34 文献标识码： A 文章编号： 1004?373X（2018）07?0170?04

Data mining based estimation model of construction project cost

FAN Wenguang1， 2

（1. Tianjin University， Tianjin 300072， China； 2. Inner Mongolia Technical College of Construction， Hohhot 010020， China）

Abstract： The cost estimation is an important research direction in the construction project management. The traditional model can′t accurately describe the change tendency of the construction project cost， and has low estimation accuracy of construction engineering cost. Therefore， a data mining based estimation model of construction project cost was designed. The mathematical model of the construction project cost estimation was established. And then the least square support vector machine （SVM） is adopted to solve the mathematical model of the construction project cost estimation. The improved particle swarm optimization （PSO） algorithm is used to optimize the model. The concrete estimation experiment of construction project cost was performed to verify the effectiveness of the model. The data mining can improve the estimation accuracy of construction project cost， and the performance of the model is higher than that of other construction project cost estimation models.

Keywords： construction engineering； quality management； cost estimation； data mining； mathematical model； project cost

0 引 言

随着经济的不断发展，人们生活水平不断提高，而住房水平是其中最为重要的一部分，使得大中小城市的建筑業发展迅速。由于材料、人工费、管理费用的不断增加，建筑工程造价的成本也相应增加，对建筑工程造价成本进行预估，为工程管理者和企业提供有价值的信息成为当前重要研究内容[1?3]。

原始建筑工程造价成本预估主要通过一些管理人员根据统计学方法进行，该过程十分复杂，极易出错，导致建筑工程造价成本预估的误差大，很难为建筑工程造价成本的管理者提供有效的信息[4]。多元线性回归模型根据建筑工程造价成本的历史数据，对相似建筑工程造价成本进行回归和拟合，比人工方法的建筑工程造价成本预估结果更加可信，但多元线性回归模型认为建筑工程造价成本是一种固定的线性增加变化趋势，这与实际情况不太相符，因为建筑工程造价成本是一种非线性变化系统，不仅有一定的线性变化趋势，同时具有一定的非线性波动，使得建筑工程造价成本预估精度有待进一步提高[5]。人工神经网络具有智能学习能力，可以对建筑工程造价成本与其影响因素之间的关系进行非线性拟合，从而描述建筑工程造价成本的变化趋势，预测精度较高，但人工神经网络的结构复杂，如何合理确定其结构没有统一的看法，且易得到“过拟合”的建筑工程造价成本预估结果[6]。数据挖掘技术是近几年发展起来的一种非线性建模方法，其中支持向量机是一种最为常用的方法，可以对建筑工程造价成本变化趋势进行深度挖掘，准确估计建筑工程造价成本与影响因素之间的联系，泛化能力强，成为建筑工程造价成本预估的主要工具[7?9]。但当建筑工程造价成本的数据较多时，支持向量机的缺陷就体现出来了，出现学习速度比较慢，有时甚至无法实现的情况[10]。

最小二乘支持向量机是一种新型的数据挖掘技术，学习速度快、泛化能力强，针对当前模型无法精准描述建筑工程造价的变化趋势，预估精度低的问题，提出基于数据挖掘的建筑工程造价成本预估模型（PSO?LSSVM），通过最小二乘支持向量机拟合建筑工程造价成本变化趋势，结果表明，数据挖掘提高了建筑工程造价成本预估的精度，预估误差小于其他建筑工程造价成本预估模型。

1 建筑工程造价成本预估的数学模型

建筑工程造价成本与许多因素相关，如人工费、材料等，设共有[n]个因素，它们可以表示为[xi，i=1，2，…，n，]建筑工程造价成本为[y]，那么两者之间的变化可以描述为：

式中[f（?）]表示建筑工程造价成本预估函数，其直接影响到建筑工程造价成绩预估的好坏。

2 数据挖掘的建筑工程造价成本预估模型

2.1 最小二乘支持向量机

设建筑工程造价成本的历史样本为[xi，yi，][xi∈Rn]为建筑工程造价成本的影响因素，即输入向量，[yi∈R]表示相应的建筑工程造价成本值，采用非线性映射[?（?）]对[xi]进行映射，建立如下的建筑工程造价成绩预估的回归模型：

[y=f（x）=ω?（x）+b] （2）

从式（2）可知，在建立准确建筑工程造价成绩预估模型时，确定最优的权向量[ω]和偏差[b，]根据结构风险最小化原理，引入松弛变量[ζi]将其变为等式约束的优化问题，具体如下：

式中[γ]表示正则化参数。

采用拉格朗日函数对式（3）求解，建立如下的拉格朗日方程：

式中[αi（i=1，2，…，N）]表示拉格朗日乘子。

由Karush?Kuhn?Tucher条件通过变换能够得到：

[0STSK+Ic bα=0Y] （5）

式中：[S=[1，1，…，1]Τ；][α=[α1，α2，…，αN]；][Y=[y1，y2，…，yN]；][K=?Τ（xk）?（xN）=K（xk，xN）]为核函数，本文选择的核函数具体如下：

[K（x，xi）=exp-x-xi22σ2] （6）

式中[σ2]表示核函数的宽度。

对式（6）进行求解，得到基于最小二乘支持向量机的建筑工程造价成本预估模型为：

[f（x）=i=1NαiK（x，xi）+b] （7）

最小二乘支持向量机的结构如图1所示，每个中间节点对应一个支持向量。

对最小二乘支持向量机的建筑工程造价成绩建模过程进行分析可知，参数[γ]和[σ2]影响建筑工程造价成本预估结果，为了提高建筑工程造价成本预估效果，采用粒子群算法确定参数[γ]和[σ2]的最优值。

2.2 粒子群算法

粒子群算法是一种模拟鸟群飞行觅食行为的算法，问题潜在解可采用一个粒子代表，粒子根据问题的求解目标确定适应度函数值，适应度函数值描述粒子位置的好坏，设[P]个粒子组成种群[s=s1，s2，…，si，…，sP]，第[i1≤i≤P]个粒子的位置为[si=si1，si2，…，siD]，[D]表示解空间的维数，在第[t]次迭代时刻，速度向量为[vti=][vti1，vti2，…，vtiD]，其最优位置为[pti=pti1，pti2，…，ptiD]，可以记为[pbest；]粒子群的最优位置为[ptg=ptg1，ptg2，…，ptgD]，可以记为[gbest；]粒子状态更新公式为：

式中：[w]表示惯性权重；[d]表示粒子维数；[c1]和[c2]为加速因子；[r1]和[r2]为[0，1]区间的随机数。

惯性权重[w]影响局部和全局的搜索性能，为了提高算法的搜索能力，保证粒子的多样性，采用自动调整的[w，]粒子多样性函数定义为：

式中[fαi（t）]为第[i]个粒子的适应度值。

[Fdiversity（t）]表示粒子的运动特性，定义非线性函数[δt]为：

式中[L]为一常数。

惯性权重[w]调整规则方式为：

式中，[εti]表示粒子[i]与最优粒子之间的距离，计算公式为：

式中[sti]为[t]时刻粒子[i]的位置。

2.3 数据挖掘的建筑工程造价成本预估步骤

数据挖掘的建筑工程造价成本预估步骤如下：

Step1：针对具体的建筑工程，通过相关资料收集其造价成本的历史数据，并对建筑工程造价成本数据做如下处理：

[x′i=xi-min（xi）max（xi）-min（xi）] （14）

Step2：初始化粒子的位置和速度，并确定它们的取值范围，将最小二乘支持向量机的参数[γ]和[σ2]映射为粒子位置。

Step3：将建筑工程造价成本预估的训练样本输入到最小二乘支持向量机学习，并对粒子位置向量进行反编码得到参数[γ]和[σ2]的值，通过训练得到每一个粒子的适应度值。

Step4：确定每一个粒子的最优位置[pti]和种群最优位置[ptg]。

Step5：对惯性权重[w]进行更新操作。

Step6：对粒子状态进行更新操作，产生新的粒子群。

Step7：通过训练样本和最小二乘支持向量机对新的粒子群的适应度值进行计算。

Step8：看是否满足结束条件，如不满足，转Step4继续执行。

Step9：根据[ptg]得到参数[γ]和[σ2]的值的全局最优组合，对建筑工程造价成本训练样本再次进行学习，建立建筑工程造价成本预估模型。

3 仿真实验

3.1 数据来源

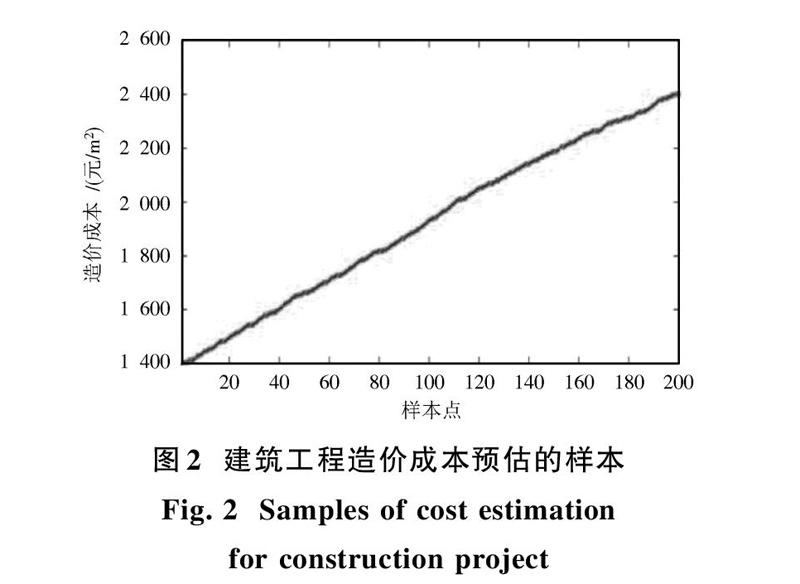
选取某市的建筑工程造价成本数据进行研究，共采集200组数据，具体如图2所示。对图2的建筑工程造价成本数据变化趋势进行分析发现，该数据具有明显线性变化特点，同时具有较强的非线性变化特点，通过嵌入定理确定建筑工程造价成本数据的延迟时间[τ]和嵌入维数[m，]并建立如下的建筑工程造价成本的预估数学模型：

根据差分熵确定图2中的建筑工程造价成本数据的延迟时间[τ=12，]嵌入维数[m=7，]最后50个数据作为建筑工程造价成本预估的测试样本，其他为建筑工程造价成本预估的训练样本。

利用最小二乘支持向量机构建建筑工程造价成本预估模型之前，先采用粒子群算法确定参数[γ]和[σ2]的值，它们分别为[γ=100，][σ2=6.725，]粒子的个数为20，[c1=c2=2，]最大迭代次数为500。

3.2 结果及分析

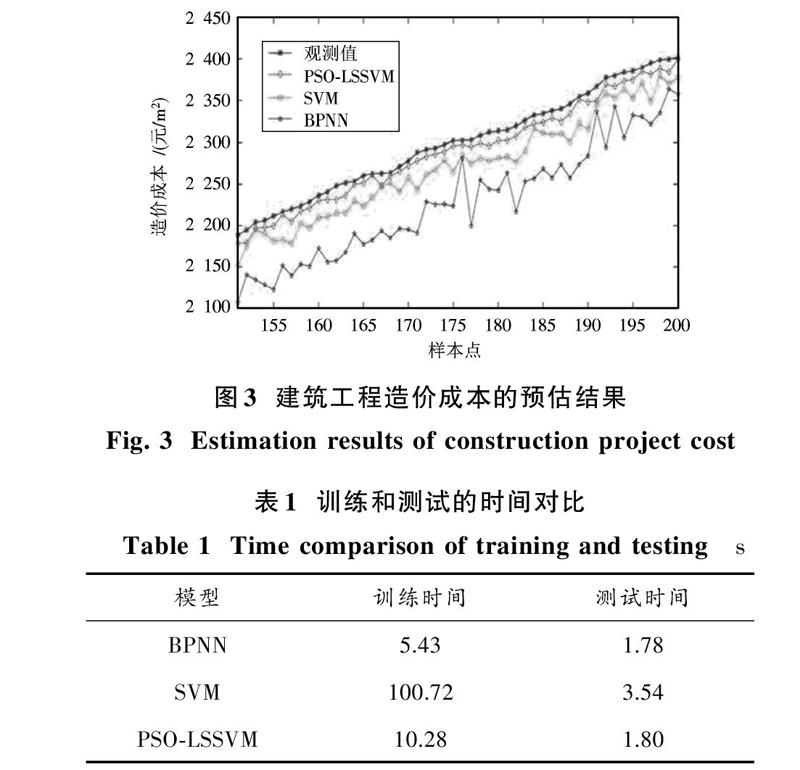
针对相同建筑工程造价成本数据集，选择BP神经网络（BPNN）、支持向量机（SVM）进行对比测试，它们的建筑工程造价成本预估结果如图3所示。从图3可以看出，BP神经网络的建筑工程造价成本预估性能最差，而支持向量机和最小二乘支持向量机的建筑工程造价成本相差不大，两者都获得了比较理想的建筑工程造价成本预估结果。对BPNN，SVM，PSO?LSSVM的训练时间和测试结果如表1所示。从表1可以看出，SVM的建筑工程造价成本预估训练时间相当长，建模效率极低，BP神经网络虽然建筑工程造价成本预估时间短，但是建筑工程造价成本预估误差大，无法满足建筑工程造价成本管理的实际应用要求，而PSO?LSSVM的建筑工程造价成本预估速度快，而且建筑工程造价成本预估效果好，具有明显的优势。

4 结 论

为了对建筑工程造价成本进行准确预测，通过数据挖掘技术对其进行建模，并通过仿真实验得到如下结论：

1） 传统方法不能高精度地拟合建筑工程造价成本變化趋势，导致建筑工程造价成本预估误差大。

2） 最小二乘支持向量机对建筑工程造价成本和影响因素之间的联系进行学习，能够有效挖掘其拟合趋势，提高了建筑工程造价成本预估的准确性。

3） 通过粒子群算法对建筑工程造价成本预估模型的参数进行优化，使得建立的模型更好地描述建筑工程造价成本的变化特点，预估结果要明显优于其他建筑工程造价成本预估模型。

4） 该模型通用性强，可以应用于其他非线性系统中预测问题的研究，具有较广的应用前景。

参考文献

[1] 陈鹏，刘亚南.建筑工程造价管理的现状与对策[J].工业工程，2015，34（48）：33?34.

CHEN Peng， LIU Yanan. Current situation and countermeasures of cost management of construction engineering [J]. Industrial engineering， 2015， 34（48）： 33?34.

[2] 梁迅.建筑工程单方造价快速估算方法综述[J].广东工业大学学报，2012，9（3）：107?110.

LIANG Xun. Review of the new methods of fast estimation of construction engineering unit square cost [J]. Journal of Guangdong University of Technology， 2012， 9（3）： 107?110.

[3] 陈小龙，王立光.基于建筑设计参数分析模型的工程造价估算[J].同济大学学报（自然科学版），2009，37（8）：1115?1121.

CHEN Xiaolong， WANG Liguang. A study on estimating approach based on analysis model for design parameters of buildings [J]. Journal of Tongji University （natural science）， 2009， 37（8）： 1115?1121.

[4] 胡六星.基于时间序列的建筑工程造价预测研究[J].太原理工大学学报，2012，43（6）：706?709.

HU Liuxing. Research on prediction of architectural engineering cost based on the time series method [J]. Journal of Taiyuan University of Technology， 2012， 43（6）： 706?709.

[5] 牛东晓，乞建勋，邢棉.建筑工程造价预测的变结构神经网络模型研究[J].华北电力大学学报，2001，28（4）：1?4.

NIU Dongxiao， QI Jianxun， XING Mian. Researches on varied structure artificial neural network model for estimating building project cost [J]. Journal of North China Electric Power University， 2001， 28（4）： 1?4.

[6] 许宁.基于模糊神经网络的建筑工程造价估计方法[J].江汉石油学院学报，2000，22（1）：87?88.

XU Ning. Estimation method of construction cost based on fuzzy neural network [J]. Journal of Jianghan Petroleum Institute， 2000， 22（1）： 87?88.

[7] 郑周练，邓绍江，高师娴，等.建筑工程造价的模糊确定[J].重庆大学学报（自然科学版），2001，24（1）：55?58.

ZHENG Zhoulian， DENG Shaojiang， GAO Shixian， et al. Fuzzy estimation on cost of project [J]. Journal of Chongqing University （natural science edition）， 2001， 24（1）： 55?58.

[8] 孟俊娜，梁岩，房宁.基于BP神经网络的民用建筑工程造价估算方法研究[J].建筑经济，2015，36（9）：64?68.

MENG Junna， LIANG Yan， FANG Ning. Research on civil construction project cost estimation method based on BP neural network [J]. Construction economy， 2015， 36（9）： 64?68.

[9] 胡晓娟.多元线性回归模型参数的STLS估计法及其在工程造价预测中的应用[J].四川建筑科学研究，2016，42（4）：142?147.

HU Xiaojuan. Structured total least squares method for multivariable linear regression model and its application in enginee?ring cost prediction [J]. Building science research of Sichuan， 2016， 42（4）： 142?147.

[10] 刘继业，陈西宏，刘强，等.基于改进粒子群优化LSSVM的卫星钟差预报研究[J].宇航学报，2013，34（11）：1509?1515.

LIU Jiye， CHEN Xihong， LIU Qiang， et al. The improved particle swarm optimization LSSVM satellite clock error prediction based on [J]. Journal of astronautics， 2013， 34（11）： 1509?1515.