基于超混沌系统的三维网格模型几何保留加密算法

李红岩 王玉惠

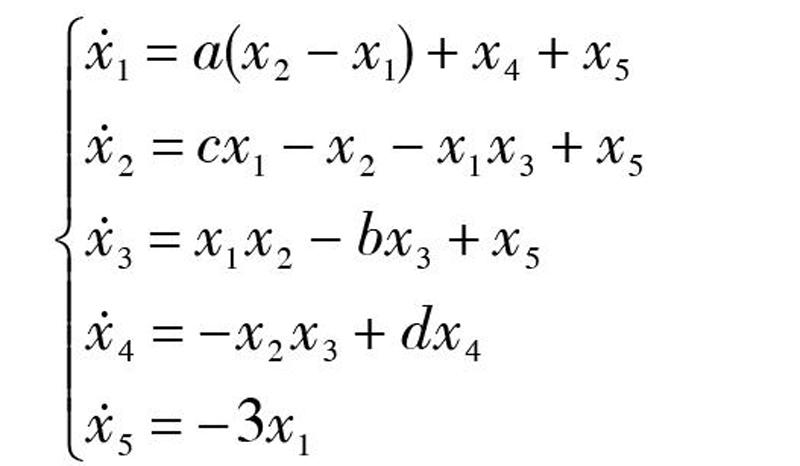
摘 要： 提出一种基于内容的三维网格模型的加密算法。加密过程将三维网格模型根据超混沌映射分别对网格面片构成置乱和网格顶点坐标扰动，从而获得加密后的三维网格模型；解密过程则利用密钥作为初始值生成超混沌系统，对网格顶点坐标和面片构成进行逆向恢复，从而获得解密后的三维网格模型。所提的加密和解密形式灵活，加密后的模型亦可渲染显示，且抗破译能力强，可对广泛应用于影视动画、艺术设计、工业设计以及医学设计等不同领域的三维网格模型进行保护。

关键词： 超混沌； 几何保留加密； 三维； 网格模型； 解密； 抗破译

中图分类号： TN711?34； TP391 文献标识码： A 文章编号： 1004?373X（2018）07?0090?03

Hyperchaotic system based geometry?preserving encryption algorithm for 3D mesh model

LI Hongyan1， 2， WANG Yuhui3

（1. Institute of Computing and Software， Nanjing College of Information Technology， Nanjing 210023， China；

2. Department of Computer Science and Technology， Nanjing University， Nanjing 210023， China；

3. College of Automation Engineering， Nanjing University of Aeronautics and Astronautics， Nanjing 210016， China）

Abstract： An encryption algorithm based on content is proposed for three?dimensional （3D） mesh model. In the encryption process， the mesh facets component is scrambled and the mesh peak coordinate is disturbed for the 3D mesh model according to the hyperchaotic mapping， so as to obtain the encrypted 3D mesh model. In the decryption process， the hyperchaotic system is generated by taking the key as the initial value to reversely recover the mesh peak coordinate and mesh facets composition， so as to obtain the decrypted 3D mesh model. The forms of encryption and decryption are flexible. The encrypted model can realize the rendering display， has high decryption resistance ability， and is used widely for 3D mesh model protection in the fields of film and animation， artistic design， industrial design and medical design.

Keywords： hyperchaos； geometry?preserving encryption； three?dimension； mesh model； decryption； decryption resistance

0 引 言

近年来，三维模型作为一种新兴的数字媒体内容，已广泛应用于影视动画、游戏设计、工业设计、医学设计以及艺术设计等多个领域。数字模型文件的造型设计和建模过程往往需要耗费设计人员的大量心血和时间，属于设计者的独创性劳动，这种智力成果具有独立版权。而在工业设计的某些特殊行业，如枪械设计、特殊工具设计以及飞机设计中数字模型的内容更需要严格保护，以免剽窃产生不良的社会影响。然而在互联网和多媒体技术高速发展的今天，数字模型很容易被复制、修改和传播，而三维打印技术的发展不仅进一步给侵权盗版者提供了机会，更为严重的是将加快侵权效率、降低侵权门槛、扩大侵权范围，这些问题也引起了国际社会的共同关注。

数字水印和加密技术可有效地应用于数字内容的版权保护。利用水印技术在多媒体内容的数据中嵌入水印信息，在发生版权纠纷时，可通过提取的水印信息确认其版权[1?4]。然而随着近年来三维打印技术的兴起和发展，在数字模型经历了打印及再扫描重建之后，水印信息将被摧毁。因此，借助加密技术对三维模型进行进一步保护，在一定程度上弥补了水印技术的不足，既可以作为水印技术的补充，又能够提供对三维模型更好的保护。针对三维模型的加密，目前大多数做法是采用传统的文件加密方式对整个三维网格模型的文件进行加密。但是这种加密方式对三维网格模型加密后，模型仅能以文件形式存在，无法对加密的三维网格模型进行渲染，更无法获知三维网格模型的任何形状或几何信息。然而，在目前的三维场景或游戏设计中，往往需要进行多人协作设计，因此很多时候对于某些模型既需要进行加密，又需要让协作者了解某处应该存在的某个形状，因此有必要设计出一种针对三维网格模型的内容进行加密和解密的技术。文献[5?6]最早提出对三维模型的几何保留，即针对内容的加密和解密方法的思想。在图像加密领域[7?9]已经产生了很多针对图像内容而不仅仅是文件本身的加密算法。

本文基于超混沌系统[10]有效实现了对三维网格模型的内容进行加密，且超混沌映射加密方式的抗破译能力强，可为广泛应用于影视动画、游戏设计、工业设计以及医学设计等不同领域的三维网格模型提供有效的保护；采用从面片构成和顶点坐标两个层面对三维网格模型进行加密，有效增强了加密效果；本文的加密和解密形式灵活，加密后的模型亦可渲染显示，保证了模型可以在场景中以加密的形式显示，且加密后模型显示范围可限定在原模型的包围盒或凸包范围内，为大场景模型设计人员协作设计提供了可能性。

1 超混沌加密算法设计

1.1 超混沌系统

在著名的Lorenz系统[11]基础上进一步提出的五维超混沌系统[10，12]，其动力学行为复杂，产生超混沌运动的参数范围较大，更加适合应用于混沌保密通信。文献[10]中提出的五维超混沌系统的动力学方程为：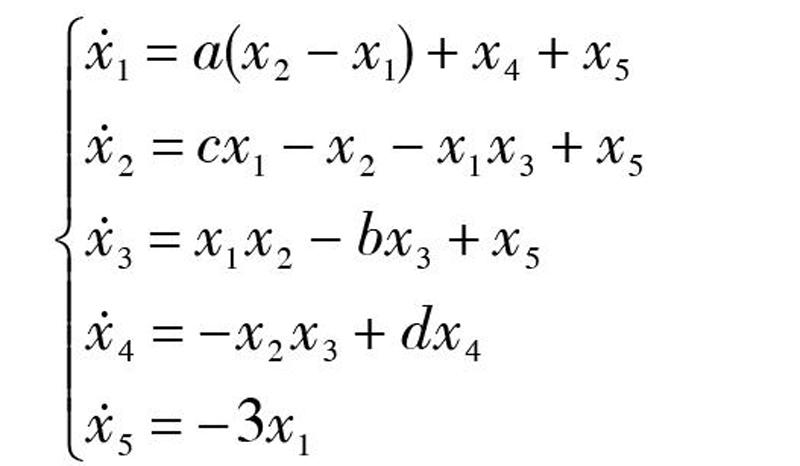

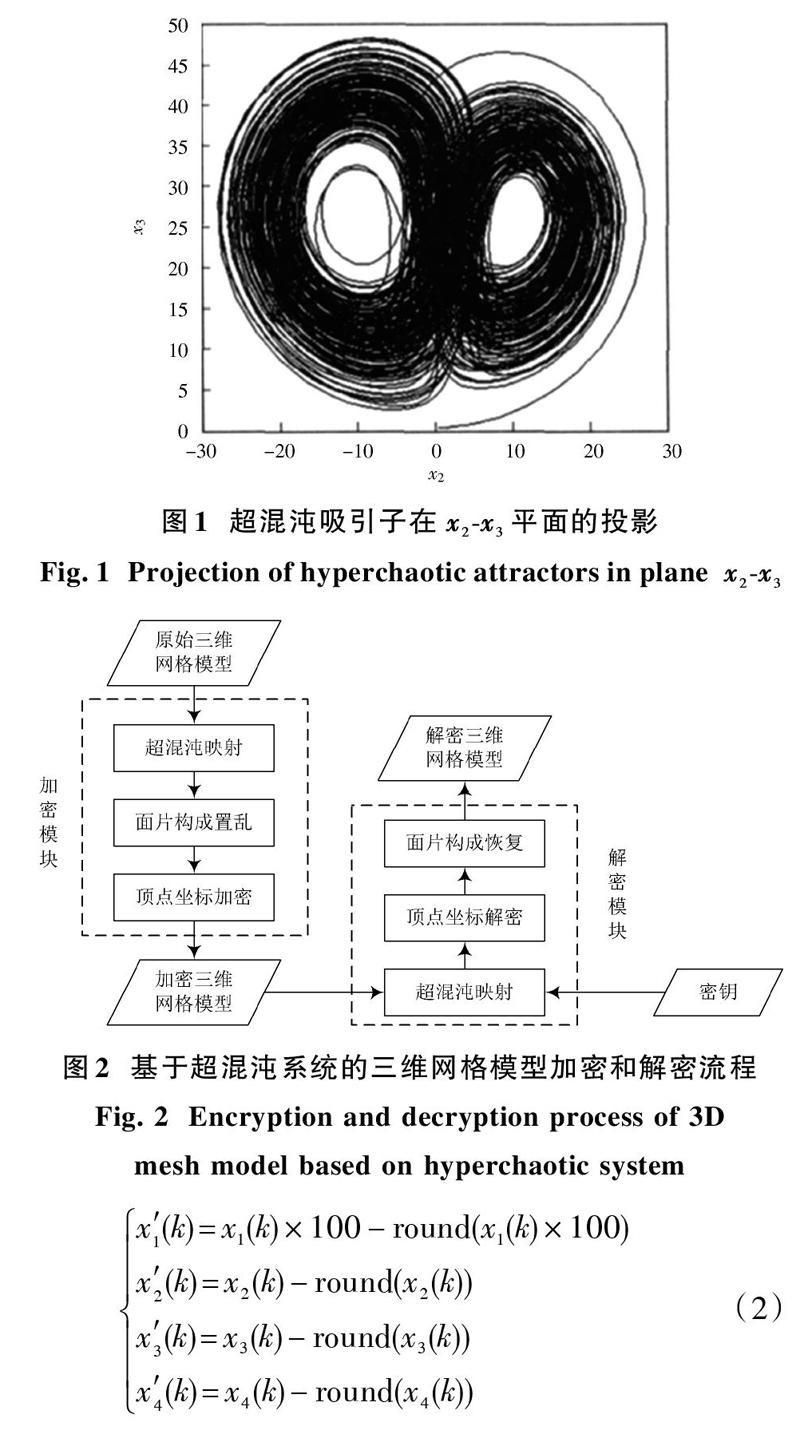
当[a=10，][b=83，][c=28，][d=-6]时，系统的Lyapunov指数为[L1=]0.239 2，[L2=]0.177 3，[L3=0，][L4=-1.539，][L5=-15.72，]其中有两个正的Lyapunov指数，并且所有Lyapunov指数之和小于零，说明系统处于超混沌状态。超混沌吸引子在[x2?x3]平面的投影如图1所示。

1.2 超混沌加密算法

采用超混沌系统对三维网格模型进行加密时，可基于超混沌映射分别对网格面片构成进行置乱加密和网格顶点坐标进行扰动加密，从而获得加密后的三维网格模型。解密过程则是将加密后的三维网格模型根据超混沌映射对网格顶点坐标和面片构成进行逆向恢复，从而获得解密后的三维网格模型，方法流程如图2所示。

三维网格模型的顶点数为[Nv，]面片数为[Nf，]顶点通过三维坐标[（x，y，z）]表示，面片构成则通过顶点序号进行标识。设定超混沌系统的初始值[x1（0）=0.9，][x2（0）=0.8，][x3（0）=0.7，][x4（0）=0.6，][x5（0）=0.5]作为系统加密的密钥。

1.2.1 超混沌序列的预处理

为利用超混沌系统对三维网格模型进行加密，首先针对[x1，x2，x3，x4]进行预处理。

式中：利用[x′1（k）]进行面片构成置乱加密；利用[x′2（k），][x′3（k），x′4（k）]进行顶点坐标扰动加密；round表示取整操作。

1.2.2 三维网格模型面片构成置乱加密

三维网格模型的面片通过指定顶点序号构成，通过将构成面片的顶点序号进行置乱，可以扰乱面片间的相关性，破坏模型的外观显示。

对按照初始值生成的超混沌系统中的[x′1（k）]进行升序排列。将原序列到升序序列的位置变换关系作为置乱序列，对网格构成的每组顶点序列进行置乱。面片构成置乱后，面片间的相关性被破坏，三维网格模型以加密形式显示。但由于此时并未改变顶点的三维坐标，因此，获取到的加密模型仍然可以通过三维模型取消网格形式，恢复到点云形式，并重新实现重构过程获取原模型的形态，加密效果并不足够强大。

1.2.3 三维网格模型顶点坐标扰动加密

为改善前述问题，采用对顶点坐标进行扰动的形式进一步对三维网格模型进行加密，以确保在未知密钥或加密模型的情况下，以任何形式都无法解密获取精确的原始模型。

根据设定的初始值生成的超混沌系统中预处理后的[x′2（k），x′3（k），x′4（k）]以及设定的扰动幅度密钥[w，]三维网格模型顶点[vj]的坐标[（xj，yj，zj）]修改为：

1.3 解密算法

对三维网格模型的解密过程，则通过传输得到的密钥产生与加密过程相同的超混沌系统，然后采用与加密过程相反的顺序，先对顶点进行解密，即将各顶点的坐标值[（xj，yj，zj）]依次减去[w×x′2（k），w×x′3（k），w×x′4（k），]获得原始坐标值。再对网格面片构成置乱进行逆向恢复，即可得到解密后的模型。

2 实 验

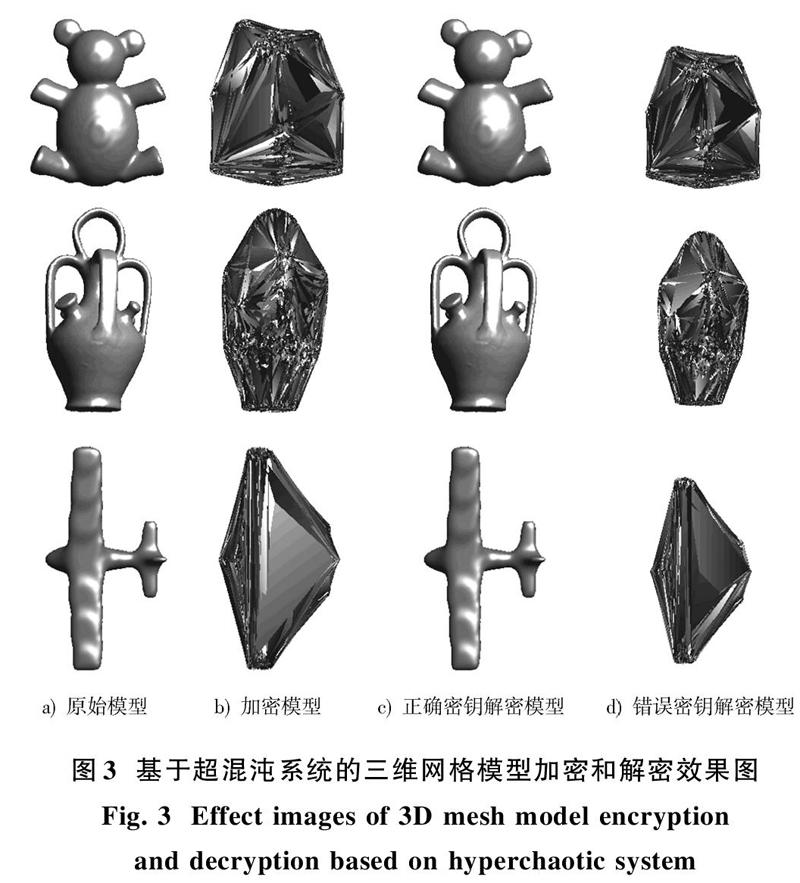
实验过程选用普林斯顿大学提供的涉及艺术设计和工业设计领域的三个模型（Teddy熊、花瓶、飞机）进行，如图3所示。给定密钥[x1（0）=0.9，][x2（0）=0.8，][x3（0）=0.7，][x4（0）=0.6，][x5（0）=0.5]作为超混沌系统的初始值，顶点扰动幅度密钥[w=0.02]。当采用錯误密钥进行解密时，即使密钥中仅个别参数发生细微变化，如[x4（0）=0.600 001，]其余密钥值均不变，依然得不到正确的解密结果（如图3d）所示），验证了本算法对密钥的敏感性，增强了加密的安全性。

3 结 语

本文实现了从面片构成和顶点坐标两个层面对三维网格模型进行加密，并控制顶点扰动的幅度。加密和解密形式灵活，加密后的模型亦可渲染显示，并保留内容几何信息，且超混沌加密方式的抗破译能力强，可为广泛应用于影视动画、游戏设计、工业设计以及医学设计等不同领域的三维网格模型提供有效的保护。

参考文献

[1] BORS A G， LUO M. Optimized 3D watermarking for minimal surface distortion [J]. IEEE transactions on image processing， 2013， 22（5）： 1822?1835.

[2] CHO J W， PROST R， JUNG H Y. An oblivious watermarking for 3?D polygonal meshes using distribution of vertex norms [J]. IEEE transactions on signal process， 2007， 55（1）： 142?155.

[3] LI H Y， SUN Z X， HE M， et al. A mesh watermarking method based on local roughness analysis [C]// Proceedings of 2015 IEEE International Conference on Software Engineering and Service Sciences. [S.l.]： IEEE， 2015： 379?383.

[4] OBUCHI R， MASUDA H， AONO M. Watermarking three?dimensional polygonal models [C]// Proceedings of the Fifth ACM International Conference on Multimedia. Washington： ACM， 1997： 261?272.

[5] ELUARD M， MAETZ Y， DOERR G. Geometry?preserving encryption for 3D meshes [J]. Proceedings of compressionet représentation des signaux audiovisuels， 2013（5）： 7?12.

[6] ELUARD M， MAETZ Y， DOERR G. Impact of geometry?preserving encryption on rendering time [C]// Proceedings of 2014 IEEE International Conference on Image Processing. Paris： IEEE， 2014： 4787?4791.

[7] 王雅庆，周尚波.基于分数阶陈氏混沌系统的图像加密算法[J].计算机应用，2013，33（4）：1043?1046.

WANG Y Q， ZHOU S B. Image encryption algorithm based on fractional?order Chen chaotic system [J]. Journal of computer applications， 2013， 33（4）： 1043?1046.

[8] 王玉惠，陈哨东，姜长生，等.基于五维超混沌的全球信息栅格图像加密算法[J].吉林大学学报（信息科学版），2011，29（1）：51?56.

WANG Y H， CHEN S D， JIANG C S， et al. Image encryption algorithm based on five?dimension hyperchaotic system for global information grid [J]. Journal of Jilin University （information science edition）， 2011， 29（1）： 51?56.

[9] 张晓强，王蒙蒙，朱贵良.图像加密算法研究新进展[J].计算机工程与科学，2012，34（5）：1?6.

ZHANG X Q， WANG M M， ZHU G L. Research on the new development of image encryption algorithms [J]. Computer engineering and science， 2012， 34（5）： 1?6.

[10] 李华青，罗小华，代祥光.一个超混沌系统及其投影同步[J].电子学报，2009，37（3）：654?657.

LI H Q， LUO X H， DAI X G. A hyperchaotic system and projective synchronization [J]. Acta electronica sinica， 2009， 37（3）： 654?657.

[11] LORENZ E N. Deterministic nonperiodic flow [J]. Journal of atmospheric sciences， 1963， 29（5）： 130?141.

[12] 魏亚东，周爱军.一个新五维超混沌系统的动力学分析[J].舰船电子工程，2012，32（7）：68?69.

WEI Y D， ZHOU A J. Dynamics analysis of a novel five?dimensional hyperchaotic system [J]. Ship electronic enginee?ring， 2012， 32（7）： 68?69.