鲁棒静态输出反馈控制律的粒子群优化设计

彭程(华北科技学院 自动化系，河北 三河　065201)

0　引　言

闭环极点位置对系统暂态性能和稳定性有重要影响，状态反馈和输出反馈是实现闭环极点配置的两种基本方式。系统能控条件下，状态反馈可以将闭环极点精确配置到指定位置，但是实际使用时需要设计状态观测器。与状态反馈方式相比，输出反馈容易实现，但是通常不能任意配置闭环极点的位置，而且设计难度大，例如文献[1-3]的方法分别需要求解李雅普诺夫方程、代数黎卡提方程和双线性矩阵不等式。

系统运行过程中参数可能会发生变化，系统性能对参数变化的鲁棒性也是控制律设计时需要考虑的因素之一。徐拴锋等[4]184-185提出了一种鲁棒静态输出反馈增益的直接优化设计方法，但是其优化初值难以确定。本文同时考虑系统鲁棒性和闭环极点配置的要求，给出了一种利用粒子群优化算法设计鲁棒静态输出反馈控制律的方法。

1　问题描述

对于线性定常系统

(1)

式中:x(t)∈Rn，u(t)∈Rm，y(t)∈Rl分别是系统状态、输入和输出；A、B和C是合适维数的矩阵；不失一般性，假设系统能控能观，且rank(B)=m和rank(C)=l成立；本文考虑的问题是设计静态输出反馈控制律:

u(t)=-Ky(t)+v(t)

(2)

将闭环系统的极点配置到合适的位置；同时，考虑到矩阵A、B和C可能存在不确定性，要求闭环系统性能对矩阵A、B和C的变化不敏感。

(3)

与状态反馈方式不同，输出反馈通常无法实现全部闭环极点的任意配置。已有研究表明[5]：对于式(1)给出的能控和能观的系统，利用式(2)给出的控制律，可以使min(n,m+l-1)个闭环极点任意接近于指定的期望位置。

为此本文将精确极点配置和区域极点配置两类要求结合起来，要求将最靠近虚轴的两个闭环极点配置到期望位置μ1和μ2；而其他闭环极点则要求位于图1所示的矩形区域中，该区域由参数α1、α2和β决定。

图1　远离虚轴闭环极点期望区域

上述极点配置要求可以通过极小化式(4)定义的目标函数实现

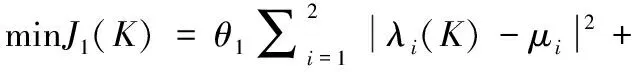
(4)

(5)

(6)

(7)

(8)

文献[6]的研究表明，闭环系统矩阵(A-BKC)的Frobenius范数越小，闭环系统对参数摄动的鲁棒性越好，即鲁棒性要求可以通过极小化式(9)定义的目标函数达成。

minJ2(K)=‖A-BKC‖F

(9)

综合式(4)和式(9)，可以将鲁棒静态输出反馈控制律设计问题表示为式(10)定义的优化问题。

(10)

2　控制律设计方法

2.1　粒子群优化算法

粒子群优化是一种群智能优化算法，它模拟了鸟类觅食的过程[7]。该算法已被用于解决齿轮箱故障诊断[8]、配电网功率协调优化[9]、声目标识别系统设计[10]等问题。

对于d维非线性优化问题：

(11)

设优化过程中种群第j个粒子的位置、速度、历史最优位置以及种群历史最优位置分别为：

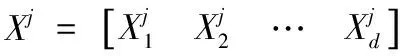
(12)

则该粒子速度和位置的第k(k=1,2,…,d)个分量按式(13)和(14)更新：

(13)

(14)

式中:w为惯性权重;c1和c2为加速度系数;r1和r2为[0,1]区间内服从均匀分布的随机数。

2.2　设计步骤

粒子群优化过程中将每个粒子的位置和速度均表示为行向量，而式(10)中待优化的输出反馈增益K∈Rm×l；为此需要建立矩阵K和行向量之间的转换关系，这里采用的方法是将矩阵K按列展开并拼接为行向量。

综上，鲁棒静态输出反馈控制律的设计步骤如下：

(2)随机生成粒子的初始位置和初始速度，并根据式(10)计算每个粒子对应的目标函数值。令每个粒子的当前位置为其历史最优位置，找到当前种群中的最优粒子，将其记为种群历史最优位置pg。令当前优化代数gen=1。

(3)令gen=gen+1。若gen>Gen，则结束优化过程，将种群历史最优位置pg转换为对应的静态输出反馈增益K并输出。

(4)对种群中每个粒子，根据式(13)和式(14)更新其速度和位置，若粒子位置和速度超出其允许的边界，则取其边界值。根据式(10)计算新位置对应的目标函数值，若新位置比该粒子历史最优位置更优，则更新该粒子的历史最优位置。

(5)找到所有粒子历史最优位置中最优的一个，若其优于之前找到的种群历史最优位置pg，则更新pg。返回步骤(3)。

3　数值算例

考虑水翼艇纵向运动数学模型[4]185：

式中：

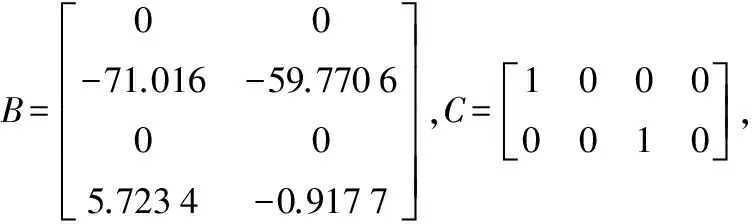
式中:h和θ分别为垂荡位移(m)和纵摇角(°);δe和δf为水翼艇的首翼角和尾翼角(°)。

设计时将最靠近虚轴的闭环极点的期望位置设为-3±3j，其余极点的期望区域参数取α1=-4、α2=-10和β=0.4，目标函数式(10)中参数θ1=100、θ2=10 000。

加速度系数c1和c2对粒子群优化的性能有显著影响，这里取文献[11]中推荐的c1=c2=2。粒子群优化的其他参数为：粒子数目N=50，最大优化代数Gen=1 000；惯性权重w前750代由0.9线性下降至0.4，其后保持不变；粒子每个分量的取值范围均为[-20,20]，每个速度分量的范围均为[-20,20]。

一次粒子群优化得到的种群历史最优位置对应的目标函数J(K)随优化代数gen的变化过程如图2所示，可以看到500代左右算法收敛到一组解。优化结束时目标函数值J=49.1974，求得的输出反馈增益:

此时，闭环极点位于-3.087 1±3.027 4j、-4.000 0和-4.456 4，即本文方法设计的控制律可以满足区域极点配置要求，也较好地满足了精确极点配置要求。

图2　最优目标函数变化过程

文献[4]185将四个闭环极点的期望位置指定为-3±3j、-5和-6，利用改进的Powell算法得到的鲁棒输出反馈增益:

计算可得‖A-BK1C‖F=47.528 6，‖A-BK2C‖F=61.004 5，本文设计的闭环系统在鲁棒性度量方面有显著改进。

在垂荡位移h=1 m，纵摇角θ=1°情况下，两控制律作用下闭环系统的状态响应曲线如图3所示。由图可知两种情况下闭环系统响应的快速性差别不大，本文设计的闭环系统响应更加平稳。

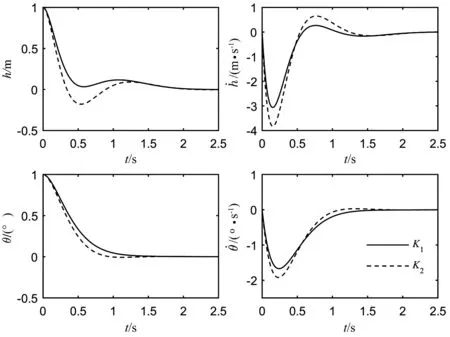
图3　闭环系统状态响应比较图

将系统矩阵A的对角线元素摄动为原始值的120%，计算参数摄动后闭环系统的状态响应，并与未摄动系统的状态响应比较如图4所示。由图可知在本文设计的控制律作用下，摄动前后系统状态响应的快速性和平稳性变化不大，反映出闭环系统的鲁棒性。

图4　摄动前后系统状态响应比较图

4　结束语

静态输出反馈控制律设计是线性系统理论的基本问题之一，至今尚未完全解决。本文通过合理构造目标函数，将鲁棒静态输出反馈控制律设计问题转化为优化问题，并利用粒子群优化算法进行求解。水翼艇系统的设计结果表明该方法简单、直观、易于实现，能够满足极点配置和鲁棒性的要求。

参考文献：

[ 1 ] SUBUDHI B, MUKHERJEE K, GHOSH S. A static output feedback control design for path following of autonomous underwater vehicle in vertical plane[J]. Ocean Engineering, 2013, 63(5): 72-76.

[ 2 ] TROFINO NETO A, KUCERA V. Stabilization via static output feedback[J]. IEEE Transactions on Automatic Control, 1993, 38(5): 764-765.

[ 3 ] 王远钢. 基于BMI方法的扇形极点配置输出反馈控制[J]. 自动化学报, 2008, 34(9): 1192-1195.

[ 4 ] 徐拴锋, 周玲, 杜秀华, 等. 基于输出反馈的鲁棒控制器优化设计及仿真[J]. 计算机仿真, 2010, 27(10): 183-186.

[ 5 ] 郑大钟. 线性系统理论[M]. 北京: 清华大学出版社, 1990.

[ 6 ] DICKMAN A. On the robustness of multivariable linear feedback systems in state-space representation [J]. IEEE Transactions on Automatic Control, 1987, 32(5): 407-410.

[ 7 ] SHI Y, EBERHART R. A modified particle swarm optimizer[C]// IEEE World Congress on Computational Intelligence, Anchorage, Alaska, USA, 1998: 69-73.

[ 8 ] 赵卫伟, 潘宏侠. 基于PSO参数优化的支持向量机齿轮箱故障诊断研究[J]. 机床与液压, 2014(7): 152-154.

[ 9 ] 黄素娟, 祝进, 王海龙. 含分布式光伏的配电网功率协调优化[J]. 电气自动化, 2016, 38(6): 31-34.

[10] 刘亚雷, 于艳美, 孟春宁. 基于粒子群神经网络的声目标识别系统设计研究[J]. 电气自动化, 2016, 38(2): 115-118.

[11] EBERHART R C, SHI Y. Comparing inertia weights and constriction factors in particle swarm optimization[C]// Proceedings of the 2000 Congress on Evolutionary Computation, La Jolla, California, USA, 2000: 84-88.