双相介质薄砂层的地震反射特征分析

杨　春,王　赟,陈业全,张秉铭

(1.中国地质大学(北京)地球物理与信息技术学院,地质过程与矿产资源国家重点实验室MWMC研究组,北京100083;2.中国石油化工股份有限公司石油勘探开发研究院,北京100083;3.中国石油化工股份有限公司油田勘探开发事业部,北京100728)

目前油气地震勘探所面对的主要储层类型中,无论是砂岩储层还是碳酸盐储层,都是固体和流体组合的双相介质。地震波在双相介质中的传播特征不同于单相介质的情况,双相介质中的弹性波传播方式更为复杂也更贴近实际地质情况。我国绝大多数中、新生代陆相含油盆地大都以砂、泥岩沉积为主,以薄层的形式存在,其厚度远低于目前地震勘探技术的垂向分辨率[1]。因此,研究基于双相介质理论或等效理论的含油气薄砂岩储层的地震反射特征,对寻找薄岩性油气藏具有十分重要的意义。

关于双相介质的研究可以追溯到20世纪50年代,GASSMANN[2]给出了用于解释孔隙流体对岩石弹性性质作用的Gassmann方程,建立了骨架体积模量、干燥岩石体积模量、孔隙流体体积模量、流体饱和岩石体积模量以及孔隙度的关系。BIOT[3-4]改进了Gassmann的流体饱和多孔介质理论,即Biot-Gassmann理论,为双相介质波动理论的研究建立了基础。GEERTSMA等[5]推导了Biot理论公式中的低、中频近似公式。PLONA[6]证实了Biot理论的正确性。MAVKO等[7]和MURPHY等[8]提出了喷流机制,认为喷流机制在完全饱和或者部分饱和的岩石中普遍存在。DVORKIN等[9]结合宏观全局流动的Biot模型和局部流动的喷射模型提出了Biot-Squirt(BISQ)模型。WANG[10]指出,由于对大多数储层岩石来说零频率和非限定频率之间计算出的速度差别通常不到3%,Biot理论计算出的速度对频率几乎没有依赖关系,因此流体替换分析经常采用的是Gassmann方程,而非Biot的全频理论。在国内,有关双相介质的地震波传播理论及其应用研究也得到了重视和发展,并取得了一些成果。门福录[11]探讨了波在饱和流体孔隙介质中传播的问题。王尚旭[12]给出了单阻抗差界面的双相介质反射和透射系数方程,并实现了双相介质中地震波传播的有限元解法。WU等[13]和乔文孝等[14]研究了声波在双相介质分界面上的反射和透射规律。张应波[15]探讨了Biot理论在石油地震勘探中的应用。陈信平等[16]指出:虽然Gassmann方程有一些限制条件,但仍是岩石物理研究强有力的工具,现有修正Gassmann方程的方案也只是在二级近似上修正了Gassmann方程的预测结果,且常常附加更多的假设条件。SHI等[17]证明了在实验室低频范围内(0～100Hz),Gassmann方程是成立的,同时传统的Gassmann理论也适用于频率不高于104Hz的声波测井。撒利明[18]以多相介质理论的实验室数据为基础,提出对应低频共振和高频吸收的时窗图区域即为高产油气区。卢明辉等[19]探讨了双相介质含不同流体时的地震反射规律,研究了孔隙度、饱和度等储层参数对纵波衰减的影响。张聿文等[20]研究了基于单相与双相介质拟海底单界面反射的AVO特征。夏红敏等[21]利用Gassmann方程对含气地层进行了流体替换计算,分析了孔隙度及含气饱和度变化对地层AVO的影响。林凯等[22]利用Gassmann等效介质理论,从波动方程的角度刻画了复杂鲕滩储层模型的地震响应。郭智奇等[23]利用Gassmann流体置换方程分析了薄储层的孔隙度和含油、含气饱和度等因素对P波速度、S波速度和介质密度的影响,并利用粘弹性各向异性理论研究了0～50°范围内薄储层物性参数与地震反射特征之间的关系。印兴耀等[24]针对勘探生产中缺乏速度测井资料的情况,利用Gassmann方程建立岩石物理模型,并在此基础上提出了速度反演预测方法。张世鑫等[25]结合Biot-Gassmann多孔弹性介质理论重新推导了Aki-Richards反射系数近似方程,得到了包含Russell流体因子的孔隙弹性介质反射系数线性近似方程。总结以上研究可以发现:除了郭智奇等[23]针对砂-页岩薄储层的研究外,现有的双相介质地震反射理论及应用的研究大都是针对单阻抗差界面或厚的层状介质,Gassmann方程仍是流体替换技术中应用最为广泛的理论基础,得到业界的普遍认可;其次,研究分析含油气薄砂岩储层的地震响应特征并判断其中的流体性质,对提高油气预测的精度有着非常重要的意义。

本文拟针对围岩为泥岩的双相介质薄砂层模型,从Gassmann方程出发,对目标薄砂层进行流体替换,计算出薄砂层在不同孔隙度、流体类型及饱和度下的纵、横波速度及密度;利用薄层位移反射透射系数矩阵方程求取薄砂层的地震PP波及PS波反射系数,分析频率、孔隙度及流体性质对薄砂层地震响应的影响,从而尝试回答薄砂层中流体是否可预测这一基本问题。

1　方法原理

1.1　薄层位移反射透射矩阵方程

对于如图1所示的各向同性弹性单薄层模型,YANG等[26]给出了P波入射情况下的薄层位移反射透射矩阵方程:

(1)

方程(2)中,A=[aij],i,j=1,2,3,4,且有:

图1　薄层模型

1.2　流体替换理论

流体替换是储层岩性研究及流体识别的工具之一,在AVO分析中起了重要的作用。流体替换的理论基础是Wood方程[27]及Gassmann方程[2]。在已知充填流体的体积模量及密度的情况下,根据Wood方程可以获得混合流体的等效体积模量Kf及密度ρf。同时,在给定孔隙度、基质体积模量、干岩体积模量的情况下,根据Gassmann方程可求得饱和流体介质的体积模量Ksat,剪切模量μsat及密度ρsat。在此基础上,利用以下公式便可获得饱和流体介质的纵、横波速度:

(3)

基于流体替换理论,我们可以获得薄层介质的纵、横波速度及密度等参数,将其代入公式(1)中便可求得双相介质薄层的等效反射透射系数。

2　模拟与分析

根据MAVKO[28]给出的矿物体积模量、剪切模量及密度,设定薄砂层各层岩石基质的弹性模量等参数,如表1所示。

表1　岩石基质的模量及密度

变化中间砂层的孔隙度为:0,0.01,0.03,0.05,0.07,0.09,0.12,0.20,0.25和0.30,其中孔隙度为0时即为单相介质情况。同时,变化孔隙流体的类型如表2所示,为了论述方便,下文以序号表征各流体类型。油、气、水的体积模量与密度如表3所示,7种流体组合情况下饱和流体的等效体积模量及密度如表4所示。入射波频率取10,30,50,80,100Hz,中间层厚度设定为10m。

表2　油、气、水饱和度、组合类型及序号

注:So为油的饱和度;Sg为气的饱和度;Sw为水的饱和度。

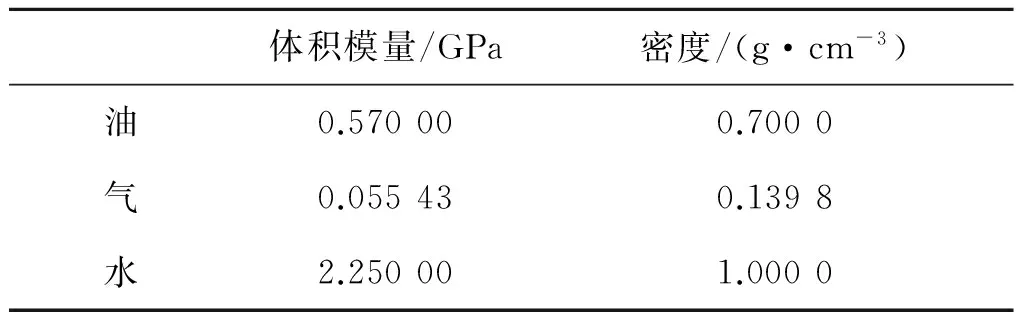
表3　油、气、水的体积模量及密度(据参考文献[29])

表4　不同组合类型的饱和流体等效体积模量及密度

2.1　孔隙度及流体性质对砂岩弹性参数的影响

利用流体替换理论求解双相介质砂层的等效纵波速度、横波速度、密度以及泊松比,不同孔隙度及饱和度下中间砂岩的弹性参数如图2,图3所示。

由图2和图3可看出,中间砂层的纵、横波速度及密度都随着孔隙度的增加而降低,且降低幅度有加快的趋势;在孔隙度为0.30的情况下,纵、横波速度幅值相比无孔隙情况都降低了40%以上,密度幅值相比无孔隙情况降低了23%左右。相同孔隙度下,通过不同油、气、水组合类型对比可知:密度对油、气、水组合类型较为敏感,横波速度次之,纵波速度最不敏感;纵、横波速度在含气饱和度100%(类型2)情况下高于其它流体充填情况,密度在含气(类型2,4,5,6,7)情况下低于其它流体充填情况,且随着含气饱和度的增加而降低。同时,当储层含气时,泊松比较相同孔隙度下不含气情况(类型1,3,5)略低。

图2　中间层弹性参数纵波速度(a)和横波速度(b)的变化

图3　中间层弹性参数密度(a)和泊松比(b)的变化

2.2　流体对薄砂层地震响应的影响

为了直观地说明流体对薄砂层地震响应的影响,取50Hz的雷克子波为震源子波,利用反射率法模拟单相介质及含流体介质的PP波及PS波地震剖面。以孔隙度12%、含油饱和度100%(类型1)为例,地震剖面如图4和图5所示。

由图4和图5可知,流体的存在会一定程度上影响薄砂层的地震响应。孔隙度12%、含油饱和度100%情况下,地震反射PP波及PS波的振幅能量弱于相应的单相介质薄砂层PP波及PS波振幅能量,且流体对反射PP波地震响应的改造作用强于PS波。

同时,为了讨论不同孔隙度、流体性质及入射波频率对薄砂层地震反射的影响,本文以下内容将忽略地震子波的影响,直接对不同情况下的PP波及PS波反射系数进行讨论。

2.3　孔隙度对薄砂层反射系数的影响

以入射波频率为50Hz、含油饱和度100%(类型1)的情况为例,分析孔隙度对反射PP波、PS波振幅及相位的影响,如图6和图7所示。

由图6和图7可知,当孔隙中的流体为油时,对于反射PP波而言,中、低孔隙度(0,0.01,0.03,0.05,0.07,0.09,0.12)情况下振幅随着入射角的增大先降低后升高;高孔隙度(0.20,0.25,0.30)情况下的反射系数振幅随入射角的变化趋势没有明显的规律性。在近垂直位置处,孔隙度为0.20和0.25时的振幅低于中、低孔隙度的情况,而孔隙度为0.30时的情况与中、低孔隙度情况相当。同时,低孔隙度范围内,孔隙度对反射PP波的振幅影响主要体现在小角度及中等角度范围(0～60°);在大角度范围内(60°～90°),孔隙度的改变未引起明显的PP波振幅变化。对于反射PP波相位而言,中、低孔隙度下的相位在小角度及大角度范围内基本相同,在中等角度范围(30°～50°)内相位随着孔隙度的增大而降低,且降低幅度随孔隙度的增加而增大;在高孔隙度(0.20和0.25)的情况下相位出现正、负极性的跳变,而孔隙度为0.30的情况下地震反射相位为负相位,与中、低孔隙度情况明显不同。对于反射PS波而言,除孔隙度0.30情况外,反射振幅随着孔隙度的增加而降低,且中、低孔隙度情况下降低幅度很小,在近垂直或水平入射情况下几乎相同,孔隙度为0.20和0.25的情况较中、低孔隙度幅值降低幅度较大;反射相位整体变化趋势一致,孔隙度越大,由负相位倒转为正相位对应的入射角越大。孔隙度为0.30时,PS波反射振幅及相位的变化趋势不同于其它情况,这是由于该孔隙度下砂岩的纵波速度低于围岩的纵波速度,导致薄层极性由(+,-)变为(-,+)。

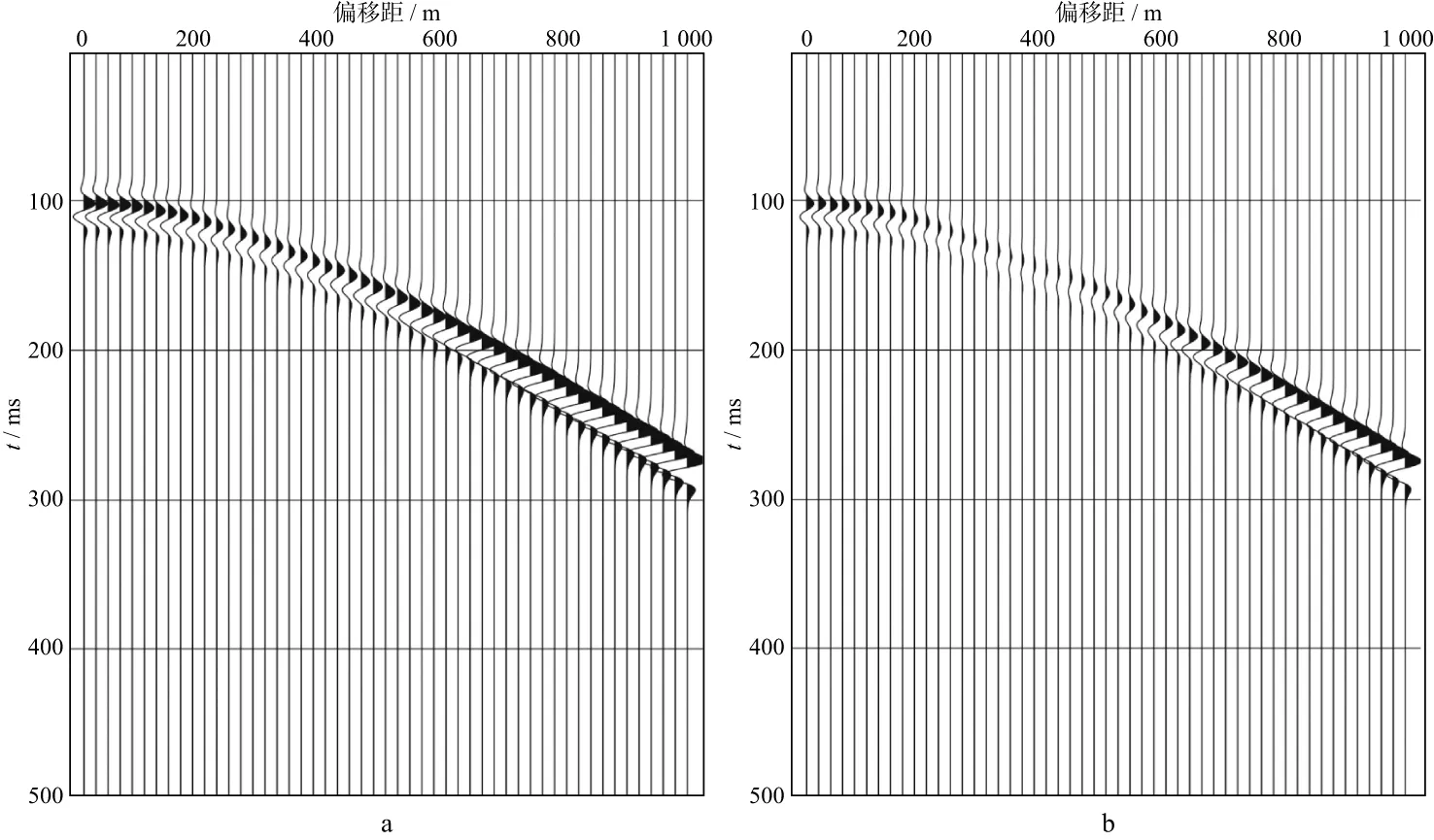
图4　单相介质薄砂层(a)与含流体介质薄砂层(b)PP波地震剖面对比

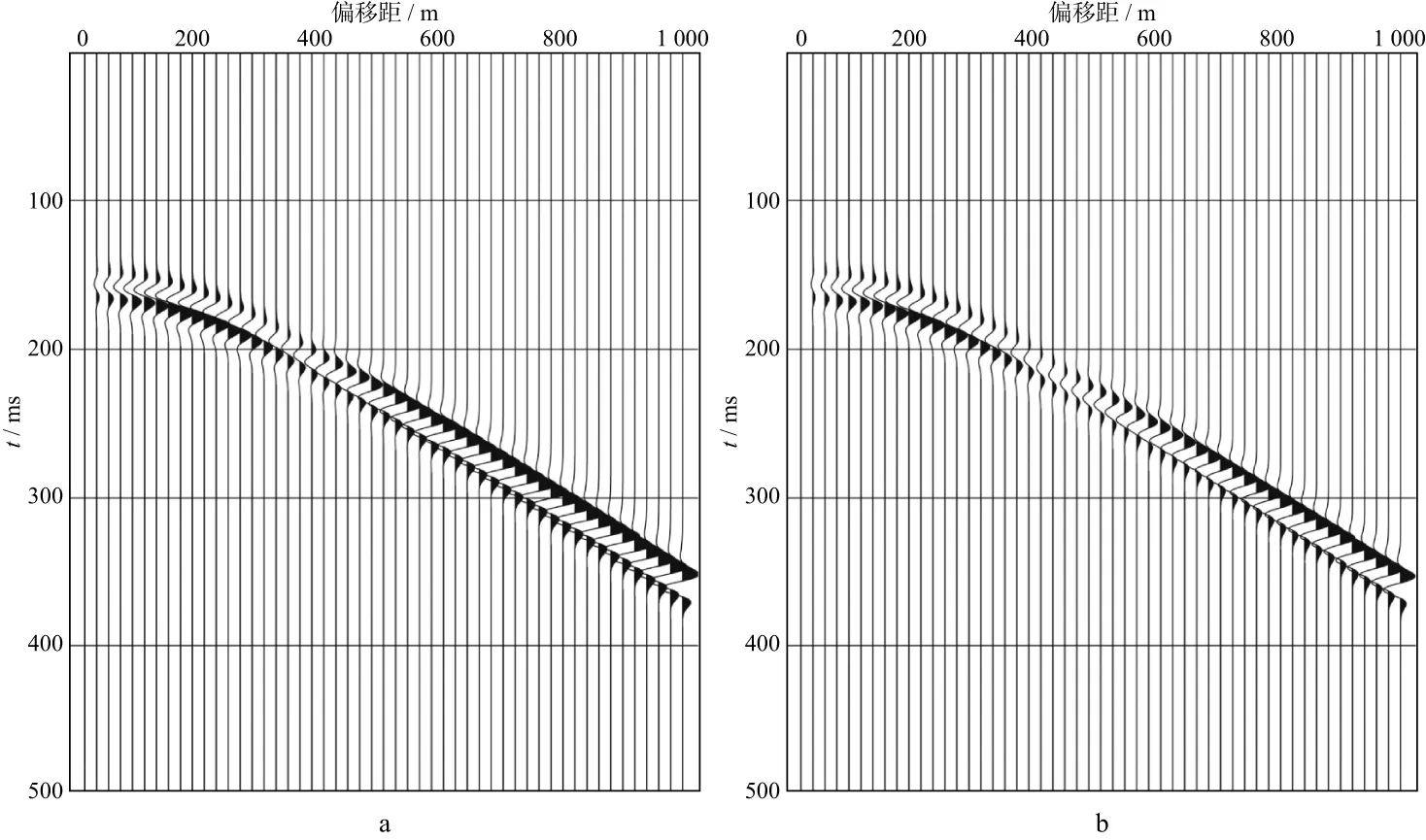
图5　单相介质薄砂层(a)与含流体介质薄砂层(b)PS波地震剖面对比

2.4　流体性质对薄砂层反射系数的影响

考虑入射波频率为50Hz时的薄层PP波及PS波反射系数随不同流体性质的变化,分析不同流体充填对薄层地震响应的影响,如图8～图11所示。

由图8和图9可知:在中、低孔隙度(<0.20)情况下,对于相同孔隙度情况而言,反射PP波及PS波的振幅在含气情况下略低于不含气情况,且反射振幅随着含气饱和度的增大而降低,但相对差异较小,反射PP波及PS波的相位对流体类型无响应;在高孔隙度(≥0.20)情况下,反射PP波振幅出现明显异常,尤其在含气时,随着孔隙度的增加,由相对不含气情况的较弱振幅过渡到相对不含气情况的较强振幅。

图10和图11为入射角30°时反射PP波及PS波的振幅及相位随油、气、水组合的变化。与入射角10°情况类似,都反映了高孔隙度时反射PP波振幅的含气异常;而在中、低孔隙度下,流体性质对反射系数的影响甚微。

图6　类型1反射PP波振幅(a)与相位(b)随孔隙度及入射角的变化(入射波频率为50Hz)(1rad≈57.30°)

图7　类型1反射PS波振幅(a)与相位(b)随孔隙度及入射角的变化(入射波频率为50Hz)(1rad≈57.30°)

图8　入射角10°时反射PP波振幅(a)与相位(b)随流体类型的变化(入射波频率为50Hz)(1rad≈57.30°)

2.5　频率对薄砂层反射系数的影响

薄层地震响应不仅与地层弹性参数有关,还与薄层厚度及入射波频率有关。由于固定厚度、增大频率与固定频率、增大厚度对薄层地震响应的影响作用一致[30],因此该部分仅以频率变化来考察频率(或厚度)对薄砂层反射系数的影响,即固定薄砂层厚度为10m,改变入射波频率为10,30,50,80,100Hz。综合考虑以上分析结果可知:孔隙度对薄层反射的影响较大,而流体类型尤其是含气性仅在高孔隙度下对薄层反射有较为明显的改造作用,因此选取类型1为例,分析入射角10°及30°情况下薄层反射PP波及PS波随入射波频率及孔隙度的变化情况,如图12～图15所示。

图9　入射角10°时反射PS波振幅(a)与相位(b)随流体类型的变化(入射波频率为50Hz)(1rad≈57.30°)

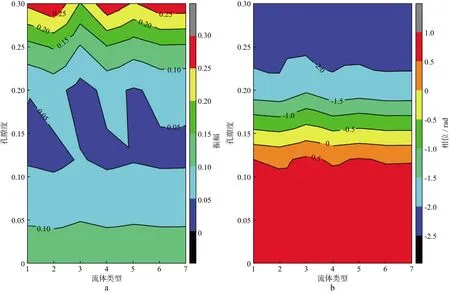
图10　入射角30°时反射PP波振幅(a)与相位(b)随流体类型的变化(入射波频率为50Hz)(1rad≈57.30°)

由图12和图13可见,当入射角为10°时,入射波频率与孔隙度共同作用影响了薄层PP波及PS波反射系数的振幅。对于PP波而言,除孔隙度为0.30的情况外,反射系数振幅随着频率的增加、孔

隙度的减小而增大,相位在中、低孔隙度下变化幅度较小。当孔隙度为0.30时,反射PP波随频率的变化与其它孔隙度情况明显不同。对于PS波而言,反射系数振幅随着频率的增加、孔隙度的减小而增大,相位在中、低孔隙度下变化幅度不大。值得注意的是,高频、高孔隙度下反射系数PP波及PS波的相位都存在数值突变,这是由于讨论的相位为主周期相位造成的。

图14和图15为入射角30°时反射PP波与PS波的振幅及相位随孔隙度及入射波频率的变化,对比入射角10°情况,不难发现:薄层AVA效应明显,入射角的不同造成了反射PP波及PS波反射系数的大小不同,且相对大小关系也有可能发生改变。不同入射角情况下,反射系数随频率、孔隙度的变化趋势一致,只是PP波变化趋势没有入射角10°时明显,而PS波变化则比入射角10°时更为明显。

图11　入射角30°时反射PS波振幅(a)与相位(b)随流体类型的变化(入射波频率为50Hz)(1rad≈57.30°)

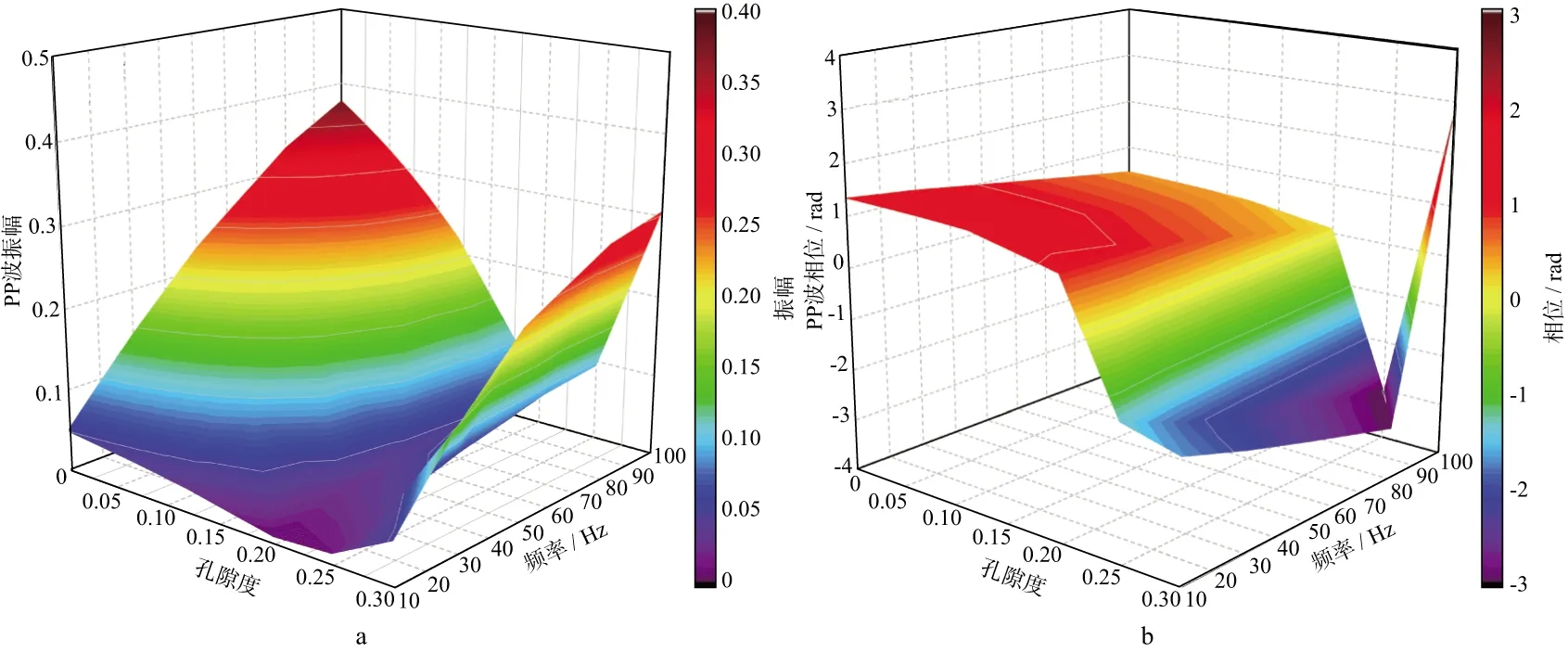
图12　入射角10°情况下反射PP波振幅(a)与相位(b)随孔隙度及频率的变化(1rad≈57.30°)

图13　入射角10°情况下反射PS波振幅(a)与相位(b)随孔隙度及频率的变化(1rad≈57.30°)

图14　入射角30°时反射PP波振幅(a)与相位(b)随孔隙度及频率的变化(1rad≈57.30°)

图15　入射角30°时反射PS波振幅(a)与相位(b)随孔隙度及频率的变化(1rad≈57.30°)

3　结论与讨论

综合双相介质薄砂岩储层在入射波频率、孔隙度及流体类型变化时弹性参数及地震反射PP波、PS波的振幅及相位的变化,可得到如下认识。

1) 弹性参数:随着孔隙度的增大,中间层砂岩的纵、横波速度及密度都会一定幅度地减小;相同孔隙度下,密度对流体类型较为敏感,横波速度次之,纵波速度最不敏感;当储层中含气时,泊松比要比相同孔隙度下不含气情况的泊松比略低。

2) 孔隙度对反射系数的影响:低孔隙度下,PP波反射振幅在小角度及中等角度范围内(0～60°)随着孔隙度的增加先降低后增大,而在大角度范围内对孔隙度的变化基本无响应;PS波反射振幅随着孔隙度的增加而降低。

3) 流体类型对反射系数的影响:中、低孔隙度下,流体性质的改变对反射PP波及PS波的影响微弱;高孔隙度下反射PP波振幅上反映出含气异常。

4) 入射波频率(或厚度)的影响:除孔隙度为0.30情况外,PP波反射振幅随着入射波频率的增大(或厚度的增大)而增大;PS波反射振幅在所讨论的孔隙度范围内都随着入射波频率的增加而增大。

综上可知:孔隙度及入射波频率共同影响薄砂层的PP波及PS波地震响应;高孔隙度下反射PP波振幅会显示出含气异常。同时,利用反演泊松比的方法可以判别储层是否含气。

[1]刘亚茹.薄互层AVO正演模拟及特征分析[D].东营:中国石油大学(华东),2007

LIU Y R.Forward modeling and characteristic analysis of thin beds AVO[D].Dongying:China University of Petroleum,2007

[2]GASSMANN F.Elastic waves through a packing of spheres[J].Geophysics,1951,16(4):673-685

[3]BIOT M A.Theory of propagation of elastic waves in a fluid-saturated porous solid:I-low frequency range[J].Journal of the Acoustical Society of America,1956,28(2):168-178

[4]BIOT M A.Theory of propagation of elastic waves in a fluid-saturated porous solid:II-higher frequency range[J].Journal of the Acoustical Society of America,1956,28(2):179-191

[5]GEERTSMA J,SMIT D C.Some aspects of elastic wave propagation in fluid-saturated porous solids[J].Geophysics,1961,26(2):169-181

[6]PLONA T J.Observation of a second bulk compressional wave in a porous medium at ultrasonic frequencies[J].Applied Physics Letters,1980,36(4):259-261

[7]MAVKO G,MUKERJI T,DVORKIN J.The rock physics handbook:tools for seismic analysis in porous media[M].New York:Cambridge University Press,1998:458-467

[8]MURPHY W F,WINKLER K W,KLEINBERG R L.Acoustic relaxation in sedimentary rocks:dependence on grain contacts and fluid saturation[J].Geophysics,1986,51(3):757-766

[9]DVORKIN J,NUR A.Dynamic poroelasticity:a unified model with the squirt and the Biot mechanisms[J].Geophysics,1993,58(4):524-533

[10]WANG Z.Y2K tutorial:fundamentals of seismic rock physics[J].Geophysics,2001,66(2):398-412

[11]门福录.波在饱和流体的孔隙介质中的传播问题[J].地球物理学报,1981,24(1):65-76

MEN F L.Problems of wave propagation in porous,fluid-saturated media[J].Chinese Journal of Geophysics,1981,24(1):65-76

[12]王尚旭.双相介质中弹性波问题有限元数值解和AVO问题[D].北京:中国石油大学(北京),1990

WANG S X.The double phase medium finite element numerical solution of elastic wave and the AVO problem[D].Beijing:China University of Petroleum (Beijing),1990

[13]WU K,XUE Q,ADLER L.Reflection and transmission of elastic waves from a fluid saturated porous solid boundary[J].Journal of the Acoustical Society of America,1990,87(6):2349-2358

[14]乔文孝,王宁,严炽培.声波在两种多孔介质界面上的反射和透射[J].地球物理学报,1992,35(2):242-248

QIAO W X,WANG N,YAN Z P.Reflection and transmission of acoustic wave at a porous solid/porous solid interface[J].Chinese Journal of Geophysics,1992,35(2):242-248

[15]张应波.Biot理论应用于地震勘探的探索[J].石油物探,1994,33(4):29-38

ZHANG Y B.Biot theory in application to seismic prospecting[J].Geophysical Prospecting for Petroleum,1994,33(4):29-38

[16]陈信平,刘素红.浅谈Gassmann方程[J].中国海上油气(地质),1996,10(2):122-127

CHEN X P,LIU S H.An preliminary introduction to Gassmann equation[J].China Offshore Oil and Gas (Geology),1996,10(2):122-127

[17]SHI G,YANG D.Determination of the elastic wave velocities in porous rocks with the change of overburden pressure and its universal significance[J].Science in China (Series D),2002,45(7):635-642

[18]撒利明.储层反演油气检测理论方法研究及其应用[D].广州:中国科学院广州地球化学研究所,2003

SA L M.The theory research and application of hydrocarbon detection based on reservoir inversion[D].Guangzhou:Guangzhou Institute of Geochemistry,Chinese Academy of Sciences,2003

[19]卢明辉,巴晶,杨慧珠.双相介质分界面上弹性波的反射与透射[J].地球物理学进展,2007,22(5):1439-1445

LU M H,BA J,YANG H Z.Reflection and transmission of elastic waves from a boundary of two-phase media[J].Progress in Geophysics,2007,22(5):1439-1445

[20]张聿文,刘学伟,李海鸥.基于单相与双相介质拟海底反射的AVO研究[J].石油物探,2004,43(3):209-216

ZHANG Y W,LIU X W,LI H O.A study of AVO responses of bottom simulating reflection in single-and two-phase media[J].Geophysical Prospecting for Petroleum,2004,43(3):209-216

[21]夏红敏,王尚旭,李生杰.含气地层的AVO响应分析—以苏4井为例[J].石油物探,2006,45(4):357-361

XIA H M,WANG S X,LI S J.AVO analysis on gas-bearing layer[J].Geophysical Prospecting for Petroleum,2006,45(4):357-361

[22]林凯,贺振华,熊晓军,等.基于Gassmann方程的鲕滩储层流体替换模拟技术及其应用[J].石油物探,2009,48(5):493-498

LIN K,HE Z H,XIONG X J,et al.Fluid substitution and it’s application in Oolitic beach reservoir based on Gassmann equation[J].Geophysical Prospecting for Petroleum,2009,48(5):493-498

[23]郭智奇,刘财,冯晅,等.薄储层的反射特性及其AVO属性分析[J].石油物探,2009,48(5):453-458

GUO Z Q,LIU C,FENG X,et al.Reflection characteristics of thin reservoirs and its AVO attributes analysis[J].Geophysical Prospecting for Petroleum,2009,48(5):453-458

[24]印兴耀,李龙.基于岩石物理模型的纵、横波速度反演方法[J].石油物探,2015,54(3):249-253

YIN X Y,LI L.P-wave and S-wave velocities inversion based on rock physics model[J].Geophysical Prospecting for Petroleum,2015,54(3):249-253

[25]张世鑫,杜向东,韩文明,等.适用Russell流体因子提取的孔隙弹性介质反射系数近似方程[J].石油物探,2016,55(2):178-187

ZHANG S X,DU X D,HAN W M,et al.A reflection coefficient approximation equation of poroelastic media for Russell fluid factor estimation[J].Geophysical Prospecting for Petroleum,2016,55(2):178-187

[26]YANG C,WANG Y,WANG Y H.Reflection and transmission coefficients of a thin bed[J].Geophysics,2016,81(5):N31-N39

[27]WOOD A B.A textbook of sound[M].Scotlan:The MacMillan Co,1955:1-578

[28]MAVKO G.Wave attenuation in partially saturated rocks[J].Geophysics,1979,44(2):161-178

[29]CORREDOR R M,SANTOS J E,GAUZELLINO P M,et al.Reflection and transmission coefficients of a single layer in poroelastic media[J].Journal of the Acoustical Society of America,2014,135(6):3151-3162

[30]杨春.薄(互)层弹性波传播特征研究[D].北京:中国科学院大学,2015

YANG C.Research on elastic wave propagating characteristics in thin beds[D].Beijing:University of Chinese Academy of Sciences,2015