基于压缩傅里叶算法的五维插值技术在改善振幅一致性中的应用

齐　鹏,胡　玮,管文华,汤国松,刘立民

(1.中国石油化工股份有限公司江苏油田分公司物探研究院,江苏南京210046;2.中国石油化工股份有限公司石油物探技术研究院,江苏南京211103)

随着地震勘探的不断深入,对地震数据的保幅性要求也越来越高。在进行叠前属性分析时,如果叠前道集数据振幅不均匀、一致性差,则会严重影响属性分析结果的准确性。可以说,如今地震资料处理的目标不仅仅是提高最终成像的质量,还应该获得振幅相对保真、一致性较好的叠前道集。然而,在实际地震资料采集过程中,由于地表条件复杂,变观现象普遍存在,炮检点分布不规则导致覆盖次数不均匀,影响了地震数据振幅的一致性[1],容易产生采集脚印和画弧现象[2]。因此,对不规则地震数据进行插值处理、提高地震数据振幅的一致性具有重要意义。

关于插值技术的研究,国内外学者已经做了很多工作[3-6]。该技术主要分为三类:①基于波场延拓的插值方法,如DMO和逆DMO结合的地震数据重建[7]。此类方法需要利用地下介质的速度信息,如果地下信息未知或精度较低,则会影响重建结果。②基于预测滤波的插值重建法,如f-x域预测滤波插值[8-9]、f-k域地震道插值[10]等。这类方法利用线性同相轴在f-x域具有可预测性的特点,从地震道已知的低频信息中提取高频成分的预测滤波算子,进而恢复出待重建地震道的高频成分。其优点是能够对地震数据进行抗假频重建,缺点是只能对规则采样的数据进行加密,不能处理非规则采样数据。③基于不同数学变换的重建方法,如Radon变换[11-13]、Fourier变换[14-16]、Wavelet变换[17]和Curvelet变换[18]等。此类方法的特点是基于数学变换理论和信号分析原理。YEN[19]在传统采样定理的基础上进行了拓展,给出了四种有限带宽信号不均匀采样的插值公式。MOORE等[20]根据Yen-4th公式提出了一种最优带宽的压缩傅里叶算法。该方法将Yen-4th公式视为波数k的函数,根据采样间隔确定奈奎斯特波数,以此奈奎斯特波数为基础,按一定间隔对波数进行递减扫描,分别计算这些波数的插值权系数的最小均方根误差,优选出满足最小均方根误差的最大波数,然后利用该波数计算插值用的权系数因子。该方法既可以处理规则采样数据又可以处理不规则采样数据,同时具有实现简单、计算效率高的特点。不足之处是没有引入抗假频机制,对存在假频的数据插值效果不佳。目前国内对该方法尚无系统的实际应用效果分析,对地震数据插值技术的研究主要集中在三维插值上,通过三维插值技术实现缺失道填补或加密空间采样。由于只考虑横、纵方向及时间,三维插值技术忽略了数据体不同偏移距和方位角信息的联系,影响了插值结果振幅的保真性,同时也无法对分布不规则的炮检点进行规则化处理。因此,五维插值技术逐渐成为了地震数据规则化处理领域的研究热点。五维插值综合考虑了地震数据的纵向、横向、时间、偏移距和方位角等五个维度的信息,具有更好的保真性,但是五维插值通常需要较大的计算量。

针对上述问题,本文采用计算效率较高的压缩傅里叶插值算法,插值时考虑了地震数据的主测线(Inline)、联络测线(Crossline)、时间、偏移距和方位角等五个维度的信息,同时针对压缩傅里叶算法不抗假频的问题,增加了局部的倾角校正处理以提高压缩傅里叶插值的抗假频能力,实现了对不规则地震数据的五维插值规则化处理,利用模型数据和实际地震资料对方法进行了测试分析。

1　方法原理

(1)

式中:基函数sinc(x)=sin(x)/x。

(2)

式中:s(xp)代表N个非等间距空间采样点序列;wp(x)代表空间采样点的加权系数,由一系列的sinc函数组成,它只依赖于采样点和插值点的空间位置。

(3)

式中:xp及xq代表不同非等间距空间采样点位置;x代表插值期望输出位置。

CHEN等[21]在上述研究的基础上推导了非等间距采样点重建信号的最小均方误差公式:

(4)

以上插值研究的内容都基于固定带宽的信号重建方法,而实际地震数据在不同插值位置的邻近地震道分布各不相同,用相同带宽插值显然不够精确。为此,MOORE[20]提出了一种压缩傅里叶算法,将插值权系数wp(x)视为空间带宽k的函数:

(5)

式中:y代表插值期望输出位置。

对任意指定的空间位置插值时,首先根据数据空间采样间隔确定最大奈奎斯特波数,以此奈奎斯特波数为基础,按一定间隔不断缩小空间波数,并根据公式(4)分别计算这些波数对应的最小均方根误差,优选出满足设定的最小均方根误差门槛值(例如10%)的最大波数,然后根据公式(5)计算该波数对应的插值权系数。这一过程也可以视为对空间带宽波数k的扫描,通过波数扫描确定最优的插值权系数,具体的波数扫描流程如图1所示。

图1　压缩傅里叶算法流程

目前大部分插值技术利用横向、纵向和时间3个维度的三维数据插值,忽略了数据在不同偏移距和不同方位角之间的联系,插值之后的数据不能很好地保真、保幅以及保持偏移距和方位角信息,影响了插值结果的振幅一致性。本文采用了五维插值技术,将插值数据分选为共中心点道集,同时考虑不同面元数据本身包含的主测线、联络线、时间、偏移距和方位角等五维信息。计算插值权系数的过程与二维、三维数据插值类似,每一维都相对独立地进行波数扫描,确定各自最优插值波数,最终插值公式如下:

(6)

式中:s为期望插值位置的输出道;i代表不同的插值维度;si为不同维度数据插值位置的邻近道;wi为不同维度数据插值的权系数。

为避免空间假频影响,常规的压缩傅里叶算法在插值前需要对数据进行动校正处理。但是在实际应用中,如果数据含有多次波或动校正速度出现偏差,则部分同相轴无法完全校平,插值时仍然会受到空间假频的干扰。因此,本文利用五维压缩傅里叶算法插值时,增加了倾角校正处理,倾角的求取思想与生成速度分析的速度谱方法类似,通过设定倾角范围,对期望插值位置的每个时间样点进行倾角扫描,计算出不同倾角的相干值,优选出相干值最大的倾角。增加倾角校正的插值算法保证了插值时同相轴的局部水平,插值公式如下。

(7)

式中:Δti代表某一维度输入样点的倾角时移。

2　模型测试

为了检验增加倾角校正的五维压缩傅里叶插值算法抗假频的能力,建立一个含有陡倾角的三维速度模型,如图2a所示,层速度分别为1500,3000,6000m/s。对该模型进行三维地震波有限差分正演模拟,上边界为自由边界条件。任意选取一炮地震数据,如图2b所示,对该炮点位置进行五维插值。插值的主要参数:波数扫描范围为最大奈奎斯特波数(由插值空间采样间隔确定)的100%～0,扫描间隔5%;最小均方误差10%;倾角扫描范围12ms,扫描间隔2ms(数据采样间隔2ms)。对比分析了常规压缩傅里叶算法与含倾角校正压缩傅里叶算法对含假频数据的插值效果。图2b为实际模拟的炮集记录,包括第一、第二个反射界面的一次反射波,以及来自第一个界面的一阶和二阶全程多次波,此外还包括来自倾斜界面的反射波。图2c为采用常规只经过动校正处理的五维压缩傅里叶算法得到的插值数据,可以看到,第一个反射界面反射波近偏移距部分和第二个反射界面的反射波插值效果较好,但是第一个反射界面的远偏移距部分反射波、多次波以及陡倾角界面的反射波插值效果不理想。这是因为利用速度模型的一次波速度对原始数据进行动校正时,无法校平多次波和倾斜界面的反射波,同时浅层反射波的远偏移距还存在动校拉伸现象,插值时受到空间假频的影响。图2d 为增加了倾角校正的五维压缩傅里叶算法插值结果。由于进行了倾角校正,保证了插值时同相轴局部水平,因此取得了较好的插值效果。对比图2b和图2d可以看出,增加倾角校正的五维压缩傅里叶插值算法获得的插值数据与理论数据差别不大,波场干净,反射波、多次波以及倾斜界面反射波与原始炮集非常接近,插值信息逼真,空间假频影响得到了较好压制。

图2　模拟数据五维插值处理a 复杂速度模型; b 实际模拟数据; c 只经过动校正处理的五维插值; d 经过倾角校正的五维插值

3　实际应用效果分析

某工区地表条件复杂,观测系统变观位置较多,地震数据采集的炮点、检波点分布如图3a所示,红色代表检波点位置,蓝色代表炮点位置。受地表因素影响,炮、检波点分布很不规则,设计满覆盖次数为42次,但为了避让障碍物而采取了变观措施,实际采集的地震数据覆盖次数从10多次到70多次不等,如图3b 所示。

最小均方根误差门槛值是压缩傅里叶插值的重要参数,要根据实际数据的信噪比特点进行选取,原始数据信噪比高时,最小均方根的门槛值可以相对较大,原始数据信噪比低时,最小均方根的门槛值要相对较小,本次实验选取的门槛值为10%。波数扫描间隔对计算效率有很大的影响,扫描间隔过小时计算时间较长,扫描间隔过大时影响插值精度,本次实验对计算效率和插值效果进行了权衡,选取的波数扫描间隔为10%。其它插值参数与模拟数据测试参数一致。图4a 为五维压缩傅里叶插值方法规则化后数据的炮、检点位置分布图,可见规则化后数据炮、检点分布更加规则。图4b为规则化后数据的覆盖次数属性图,可见数据规则化后覆盖次数的均匀性更好,部分缺失炮点得到弥补。图5为插值前后的CMP道集数据,红色实线代表炮检距分布范围,对比可以发现,五维插值规则化处理后炮检距分布更加均匀,原始数据近偏缺失得到弥补。为了更加准确地分析五维压缩傅里叶插值对炮检距的规则化作用,对该CMP道集数据作了炮检距分布属性分析,如同6所示。可以看出,原始数据存在大量变观现象,炮检距分布稀疏、不均匀,近炮检距数据缺失,而经过五维压缩傅里叶插值后的炮点位置分布规则,炮检距分布更加均匀。

图3　实际地震数据的炮检点分布(红色代表检波点,蓝色代表炮点)(a)及覆盖次数属性(b)

图4　五维压缩傅里叶方法插值后数据的炮检点分布(红色代表检波点,蓝色代表炮点)(a)及覆盖次数属性(b)

图5　五维插值前(a)后(b)CMP道集数据对比

分别对五维压缩傅里叶插值前后数据进行克希霍夫叠前时间偏移处理,图7对比了插值前后叠前时间偏移处理得到的CRP道集。图7a是五维压缩傅里叶插值前CRP道集,由于原始数据炮点、检波点空间分布不规则,导致CRP道集振幅出现跳动,一致性较差,浅中层同相轴杂乱、不连续,不利于后续的叠前属性分析及AVO处理(图中红色椭圆线圈内)。

图7b是五维压缩傅里叶插值规则化处理后的CRP道集,浅中层同相轴连续性增强,道与道之间的能量更加均衡、自然,振幅相对变化关系趋于合理。这表明经过五维压缩傅里叶插值处理后的数据炮点、检波点空间分布规则,CRP道集的振幅一致性得到改善,道集质量得到提高。

图8对比了五维压缩傅里叶插值前后的叠前时间偏移剖面。图8a是五维压缩傅里叶插值前偏移叠加剖面,由于炮检点分布不规则,存在变观、空洞等现象,浅层同相轴受到严重影响,表现为部分同相轴连续性较差(图中红色椭圆线圈内)。图8b是五维压缩傅里叶插值后的叠前时间偏移叠加剖面,对比可以发现,利用五维插值技术对炮检点位置进行规则化处理后,由于部分缺失炮点得到弥补,浅层同相轴的连续性得到明显改善。同时,由于五维插值技术改善了CRP道集质量(图7),五维插值后的偏移叠加剖面信噪比得到提高,一些复杂的断层构造更为清晰(图中黄绿色方框内)。

图6　五维压缩傅里叶插值前后CMP道集炮检距分布(红色点代表插值前;黑色点代表插值后)

图7　克希霍夫叠前时间偏移后CRP道集对比a 五维插值前; b 五维插值后

为了进一步考察五维压缩傅里叶插值规则化处理对振幅一致性的影响,对五维压缩傅里叶插值前后数据体进行了振幅属性切片对比分析(图9)。图9a 是插值前300ms处的振幅切片,由于炮检点分布不规则的影响,振幅切片存在空洞。图9b是五维压缩

图8　五维压缩傅里叶插值前(a)、后(b)叠前时间偏移叠加剖面对比

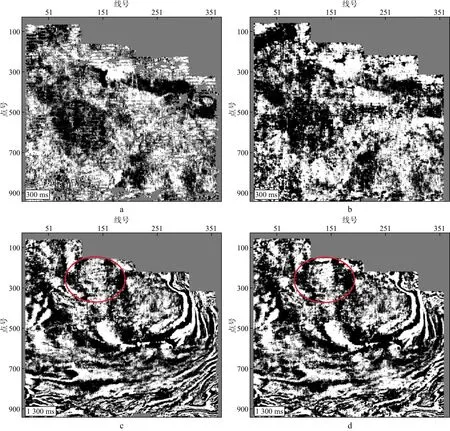
图9　五维压缩傅里叶插值前后不同时间振幅切片对比a 插值前300ms处振幅切片; b插值后300ms处振幅切片; c 插值前1300ms处振幅切片; d 插值后1300ms处振幅切片

图10　五维压缩傅里叶插值前(a)后沿层局部振幅属性对比

4　结论与认识

本文采用压缩傅里叶插值算法,考虑了地震数据的主测线、联络测线、时间、偏移距和方位角等五个维度的信息,同时增加了局部倾角校正处理以提高插值算法的抗假频能力,实现了对不规则地震数据的五维插值规则化处理。模型数据和实际地震资料处理结果表明,本文五维压缩傅里叶插值技术可以很好地降低地震数据炮检点分布不规则的影响,提高地震数据的振幅一致性和叠前道集质量,有利于后续的叠前属性分析和储层预测,在实际生产中具有较好的应用价值。

[1]李生杰,施兴觉,郑鸿明,等.复杂地表条件反射振幅一致性校正[J].地球物理学报,2002,45(6):862-869

LI S J,SHI X J,ZHENG H M,et al.The consistent correction of seismic amplitude in complicated surface area[J].Chinese Journal of Geophysics,2002,45(6):862-869

[2]CANNING A,GARDNER G H F.Reducing 3D acquisition footprint for 3D DMO and 3D prestack migration[J].Geophysics,1998,63(4):1177-1183

[3]张兴岩,潘东明,李列,等.共炮检距矢量域海底电缆数据规则化技术及应用[J].石油物探,2016,55(3):357-364

ZHANG X Y,PAN D M,LI L,et al.The regularization of ocean bottom cable data in common offset vector domain and its application[J].Geophysical Prospecting for Petroleum,2016,55(3):357-364

[4]刘喜武,刘洪,年静波.非均匀地震数据重建方法及其应用[J].石油物探,2004,43(5):423-426

LIU X W,LIU H,NIAN J B.Reconstruction of uneven seismic data and its application[J].Geophysical Prospecting for Petroleum,2004,43(5):423-426

[5]崔永福,郭念民,吴国忱,等.不规则观测系统数据规则化及在相干噪声压制中的应用[J].石油物探,2016,55(4):524-532

CUI Y F,GUO N M,WU G C,et al.Regularization of irregular geometry seismic data and its application in the coherent noise suppression[J].Geophysical Prospecting for Petroleum,2016,55(4):524-532

[6]曹国滨.频率-空间域数据规则化压制采集脚印技术研究[J].石油物探,2010,49(4):359-363

CAO G B.Study of suppressing acquisition footprint by data regularization[J].Geophysical Prospecting for Petroleum,2010,49(4):359-363

[7]RONEN J.Wave equation trace interpolation[J].Geophysics,1987,52(7):973-984

[8]国九英,周兴元,俞寿朋.f-x域等道距道内插[J].石油地球物理勘探.1996,31(1):211-218

GUO J Y,ZHOU X Y,YU S P.Iso-interval trace interpolation inf-xdomain[J].Oil Geophysical Prospecting,1996,31(1):211-218

[9]宜明理,严又生,魏新,等.f-x域抗假频道内插[J].石油物探,2001,40(2):36-41

YI M L,YAN Y S,WEI X,et al.Using anti-alias trace interpolation inf-kdomain[J].Geophysical Prospecting for Petroleum,2001,40(2):36-41

[10]MOSTAFA N,SACCHI D.f-xadaptive seismic trace interpolation[J].Geophysics,2009,74(1):V9-V16

[11]张红梅,刘洪.基于稀疏离散t-p变换的非均匀地震道重建[J].石油物探,2006,45(2):141-145

ZHANG H M,LIU H.Sparseness discretet-ptransform in irregular seismic trace reconstruction[J].Geophysical Prospecting for Petroleum,2006,45(2):141-145

[12]李晶晶,孙成禹,谢俊法.相对保幅的抛物线Radon变换法地震道重建[J].石油物探,2014,53(2):181-187

LI J J,SUN C Y,XIE J F.Seismic trace reconstruction by relative amplitude preserved parabolic Radon transform[J].Geophysical Prospecting for Petroleum,2014,53(2):181-187

[13]孙成禹,尚新民,石翠翠,等.影响地震数据相位特征的因素分析[J].石油物探,2011,50(5):444-454

SUN C Y,SHANG X M,SHI C C,et al.Analysis of influence factor on phase characteristics of seismic data[J].Geophysical Prospecting for Petroleum,2011,50(5):444-454

[14]XU S,ZHANG Y,LAMBARE G.Antileakage Fourier transform for seismic data regularization in higher dimensions[J].Geophysics,2010,75(6):WB113-WB120

[15]HINDRIKS K,DUIJNDAM A J.Reconstruction of 3-D seismic signals irregularly sampled along two spatial coordinates[J].Geophysics,2000,65(1):253-263

[16]SACCHI M D,UIRYCH T J,WALKER C J.Interpolation and extrapolation using a high-resolution discrete Fourier transform[J].IEEE Transactions On Signal Processing,1998,46(1):31-38

[17]CHOI H,BARANIUK G.Interpolation and de-noising of non-uniformly sampled data using wavelet-domain processing[J].IEEE International Conference on Acoustics,Speech and Signal Processing,1999:1645-1648

[18]HERRMANN J,HENNENFENT G.Non-parametric seismic data recovery with curvelet frames[J].Geophysical Journal International,2008,173(1):233-248

[19]YEN J L.On nonuniform sampling of bandlimited signals[J].IRE Transactions on Circuit Theory,2003,3(4):251-257

[20]MOORE I F,VAUTHRIM B.Quality control and bandwidth optimization of compact Fourier interpolation operators[J].Expanded Abstracts of 78thAnnual Internat SEG Mtg,2008,27(1):61-75

[21]CHEN D S,ALLEBACH J P.Analysis of error in reconstruction of two-dimensional signals from irregularly spaced samples[J].IEEE Transactions on Acoustics Speech & Signal Processing,35(2):173-180

[22]ÖZBEK A,VASSALLO M.Anti-alias optimal interpolation with priors[J].Expanded Abstracts of 80thAnnual Internat SEG Mtg,2010:3401-3405