孔隙度和孔隙结构对储层特性影响的定量比较

贺锡雷,林　凯,张祖豪,贺振华,2

(1.成都理工大学地球勘探与信息技术教育部重点实验室,四川成都610059;2.成都理工大学油气藏地质及开发工程国家重点实验室,四川成都610059)

在含流体储层的岩性识别和油气预测中,孔隙度和孔隙结构对储层有效弹性性质的作用和影响十分重要[1-7]。SUN等[3]的研究表明:岩石孔隙扁率(结构)的变化,可使岩石的波速变化在2000m/s以上。但目前,关于孔隙结构参数本身的研究较少,孔隙结构与孔隙度对储层弹性性质影响的定量化研究更少。究其原因,一方面是孔隙结构十分复杂,难以像孔隙度那样用简单明确的参数表示;二是在目前应用十分广泛的含流体双相介质的Gassmann流体方程中未包含孔隙结构参数,使得利用该方程来定量化研究孔隙结构的影响变得复杂和困难;三是孔隙结构的量化表示不统一,例如,ESHELBY等用孔、洞、缝的纵横比(扁率)表示孔、缝的形状,并结合与岩石压实性质有关的基质模量和泊松比等参数,形成岩石结构参数[8-11];PRIDE等[12]在构建结构参数时,以固结度表示孔、缝密度和连通性;NUR[13]以临界孔隙度的倒数表示孔隙度大小和岩石性态;还有很多学者用电性和放射性等以及某些定性方法来表示孔隙结构[1,14-15]。这些关于孔隙结构的表示方法均有各自的适用范围,在应用时如何正确选择和评价十分困难。

为克服上述困难,我们将重点研究以下几方面的问题:探讨孔隙结构参数的含义和数学表述;引入带有孔隙度和孔隙结构的岩石骨架统一模型和公式;将岩石骨架统一公式代入Gassmann流体方程中,形成可定量计算孔隙度和孔隙结构的扩展Gassmann方程;在此基础上推导出孔隙度和孔隙结构对储层等效弹性属性影响的关系式,作为定量比较二者对储层属性影响的理论基础;通过数值模拟计算,验证方法的正确性和适用性。

1　孔隙结构参数及其表述

1.1　孔隙结构的定义

地质上,孔隙结构是指岩石所具有的孔、洞、缝的大小、形状和相互连通关系,是岩石物理的重要参数。但相对岩石的孔隙度、渗透率和饱和度而言,孔隙结构参数的定义很不统一,表述也不一致:有的学者主要考虑孔、缝的大小、形状和岩石基质属性;有的学者除了考虑孔、洞、缝的大小、形状和基质属性外,还要研究与储层界面现象有关的表面张力、吸附作用、湿润度以及孔隙吼道和毛细管作用等的影响。前一类学者,主要是地质、地球物理勘探工作者。他们研究的问题相对宏观一些,且易于孔隙结构的量化表示。如前所述,他们用孔、洞、缝的纵横比(扁率)表示孔、缝的形状,以固结度表示孔、缝密度与连通性,以临界孔隙度表示孔隙度大小和岩石性态。后一类学者主要是地球物理测井和油藏开发工作者,他们对岩石孔喉等微观特征更为关注[1,14-15],涉及的问题更复杂。我们根据地震、地质问题的综合需求和易于定量表示的原则,认为孔隙结构是指孔、喉的形状、大小及其连通性。

1.2　孔隙结构参数的统一表示

HE等[16]根据现有文献中应用广泛的岩石骨架参数模型和相应的数学公式,主要包括Eshelby-Walsh公式、Pride公式、Geertsma公式[17]、Nur公式、Keys-Xu公式[18]和Krief公式[19]等,综合提炼出带有孔隙结构参数的岩石骨架参数模型:

(1)

式中:p和q(或q*)表示孔隙结构参数,在岩石骨架模型中作为孔隙度η的系数;βs为岩石基质压缩系数;βD为骨架压缩系数;μD表示剪切模量。公式(1)有如下优点:①对p,q(或q*)赋与不同的变量和数值可得到完全等价于Eshelby-Walsh,Pride,Geertsma,Nur,Keys-Xu和Krief的岩石骨架模型的表示式,具有通用性(见表1);②可获得不同于现有模型的新关系式,具有更强的适用性;③孔隙结构参数p,q综合了孔隙度大小与范围、孔隙形状(扁率)、岩石基质属性、孔隙连通性、岩石固结度等属性,使丰富的孔隙结构信息可用两个参数来表述;④将(1)式代入Gassmann流体方程,可获得既有孔隙度,又含有孔隙结构的新方程。

表1　常用岩石骨架模型及其p,q值

2　基于Gassmann流体方程的孔隙结构参数的计算

2.1　Gassmann流体方程的扩展

Gassmann流体方程是流体替换和预测的基本公式,适用于低频波传播问题的研究,广泛用于基于地震资料的孔隙流体识别研究[2,13,19-26]。问题在于该方程以岩石体积模量的倒数—压缩系数β为基本参数,未包含孔隙结构参数:

(2)

式中:βE为岩石饱和流体的有效压缩系数;βp为岩石孔隙流体的压缩系数;μE为有效剪切模量。在不考虑剪切模量μ的情况下,(2)式有5个变量,已知其中的4个,可求出另一个变量(参数)。例如,利用预先给定的βE,βD,βp和βs,可方便地求出孔隙度η。为使(2)式能够包含孔隙结构参数,我们将(1)式代入(2)式,得到新方程:

(3)

(3)式包含了孔隙结构参数,我们称其为Gassmann扩展流体方程。

2.2　Gassmann扩展流体方程的简化和实用化

考虑到流体压缩系数βp往往远大于岩石基质压缩系数[22],即βp≫βs,βp-βs≈βp,将其代入(3)式,且暂不考虑剪切模量,可获得含有孔隙结构参数的计算孔隙度的新公式:

(4)

为了方便计算孔隙结构参数,并易于同孔隙度对岩石(或储层)有效弹性性质影响进行比较,实际应用中,需要合并p和q成一个参数。我们对(4)式右边的分母添加辅助项,得:

(5)

(5)式变为:

(6)

在|x|<1的情况下,对1/(1-x)进行二项式展开,得:

(7)

舍去(7)式中x的一次方以上项,就得到了含单一孔隙结构参数S的孔隙度计算公式:

(8)

由(8)式可得孔隙结构参数的计算公式:

(9)

饱和岩石有效弹性的计算公式:

(10)

如果舍去(7)中x二次方以上项,则得:

(11)

考虑到在大多数情况下,q/(p+q)≈1或者0,见表1。当其值为0时,(11)式退化成(8)式;当其值为1时,得:

(12)

由于βE的值恒大于βs[22],所以(12)式的精度满足大多数实际问题的要求。

2.3　误差分析

计算孔隙度的公式(8)和公式(12)以及在此基础上推导的计算孔隙结构和储层饱和弹性参数的公式均存在一定的误差。该误差取决于公式(7)的截断误差。由于(7)的变量,并且其值总是小于1,则截断误差取决于x小于1的程度,因为q/(p+q)≈1。可按实际问题中βE和βs的值确定x。若x≤0.1,则舍去x2以上项,其误差不超过1%;若x≥0.1,则需要保留x的更高次方项。

3　孔隙度和孔隙结构参数对岩石有效弹性性质影响的比较

孔隙度和孔隙结构对饱和岩石等效弹性性质的影响是一个倍受关注的问题。如果孔隙结构相对孔隙度对岩石等效弹性的影响很小,则无须考虑孔隙结构的影响,否则,应当仔细估计其作用。下面我们通过定量分析得出孔隙度和孔隙结构参数在什么情况下对岩石弹性性质有什么样的影响。

3.1　定量比较公式的推导

如前所述,在实际问题中存在:βp≫βs,βs<βE,(8)式可进一步简化为:

(13)

由(13)式得:

(14)

从(14)式出发,分别求取孔隙结构S和孔隙度η对饱和流体有效模量βE的偏导数。得:

(17)

我们称R为孔隙结构相对孔隙度对储层有效弹性性质的影响因子。此因子是从简化公式(13)出发推导出来的,但是仍然具有一般性,如果从精度更高的公式(12)出发进行比值R的推导,我们可得到与(17)式完全一样的结果,只是过程复杂一些,见附录A。

3.2　影响因子R值的大小比较和数值模拟分析

(17)式简单、明了,但是内容十分丰富,能够用它全面评价孔隙度和孔隙结构对储层弹性的不同影响。按R值的大小,得到了下述3种基本情况:

1)R值较大时,孔隙结构对岩石饱和流体有效压缩系数βE的影响大于孔隙度的影响。这对应孔隙度比较大,孔隙结构比较小的情况(参看公式(17))。图1是孔隙结构S与岩石有效压缩系数βE的交会图,孔隙度η作为参量。该图是按附录中的公式(A4)计算的,式中的基质压缩系数βs一般按目标地层的平均值给出,也可根据岩石的主要矿物成分,通过查表获得[10],我们在计算中采用的βs值为14×10-3GPa-1,这是一种通用值。由图1可见,η=0.2的曲线是3条曲线中η值最大的,而该曲线横坐标所对应的孔隙结构S是3条曲线中最小的(横坐标范围为1～8),曲线陡度最大,岩石有效压缩系数βE随孔隙结构的增加,变化值达400×10-3GPa-1以上。说明孔隙结构的微小变化,会引起βE的很大变化。在此种情况下,孔隙结构对岩石弹性性质的影响起主要作用。作为对比,还可看到,η=0.1曲线的横坐标范围为1～18,该曲线的陡度中等;η=0.05曲线的陡度较缓,孔隙结构变化量ΔS达到35,引起的压缩系数变化量ΔβE相对于前者,减小了一倍(变化值达200×10-3GPa-1)。说明在不同条件下,孔隙结构对岩石弹性性质的影响可能成倍增加。

2)R值较小时,孔隙度对岩石饱和流体有效压缩系数βE的影响大于孔隙结构的影响。这对应孔隙结构参数比较大,孔隙度比较小的情况。图2是孔隙度η与岩石有效压缩系数βE的交会图,孔隙结构S作为参量,βE的取值与第1种情况一样。同样,在图2 中,S=15的那条曲线是4条曲线中S最大的,该曲线横坐标的孔隙度最小,而且曲线最陡,孔隙度的微小变化会引起βE的很大变化。此时孔隙度对岩石弹性性质的影响起关键作用。然而这种情况会发生变化,在S值逐渐减小时,所对应曲线的斜率随之减小。S=1时,随孔隙度增大,βE几乎不变,孔隙度对岩石弹性性质没有影响,转化成第1种情况。

3)R值适中时,孔隙结构与孔隙度对饱和流体储层等效模量βE的影响相当。图1和图2是利用本文推导的公式计算的。为验证公式的正确性和上述结论的合理性,我们利用广泛应用的Keys-Xu模型[18]计算了孔隙度和地震纵、横波速度交会图,见图3。图中的参数为孔隙的扁率,它与本文的结构参数呈反比:较小的扁率对应较大的结构参数。由于岩石纵横波速度与弹性参数存在确定的转换关系,因此孔隙度与地震速度交会图等价于孔隙度与岩石弹性参数的交会图。由图3可见,在结构参数较大(扁率为0.01)和孔隙度较小(小于0.1)时,曲线斜率大,纵波速度由5000m/s以上,减小到2000m/s以上,减小量为2000～3000m/s,横波速度由3000m/s以上降低到不到1000m/s,减小量也为2000～3000m/s。说明孔隙度对弹性的影响起主要作用,类似于前面的第2种情况。同时还可看到,随着孔隙度增大,在扁率固定时,曲线迅速变缓,孔隙度引起的速度变化很小,起主要作用的是扁率(孔隙结构),与第1种情况类似。但无论那种情况,孔隙结构和孔隙度均可引起地震纵、横波速度产生2000～3000m/s变化。这与我们的研究结果一致,也与其它学者的研究相符[3]。

需要说明的是,对于前面的第3种情况(R值适

中时,孔隙结构与孔隙度对饱和流体储层有效模量βE的影响相当),需要判断什么是“适中”。为此我们对S进行归一化处理,使其数值像孔隙度一样,也分布在0和1之间。这样在R=1时,孔隙结构与孔隙度对饱和流体岩石有效模量βE的影响相当。同样,R<1,孔隙度的贡献大于孔隙结构;R>1,则相反,孔隙结构的作用大于孔隙度的作用。S归一化处理后,R的作用很好记忆和理解,便于问题的分析。但在制作模版时,还需要利用未归一化的S值。

图1　孔隙结构与岩石饱和压缩系数交会分析结果

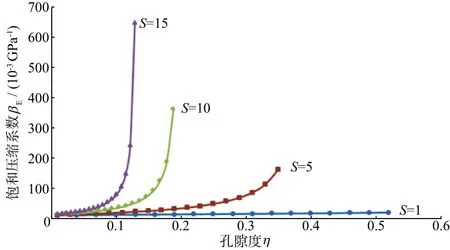
图2　孔隙度与饱和压缩系数交会分析结果

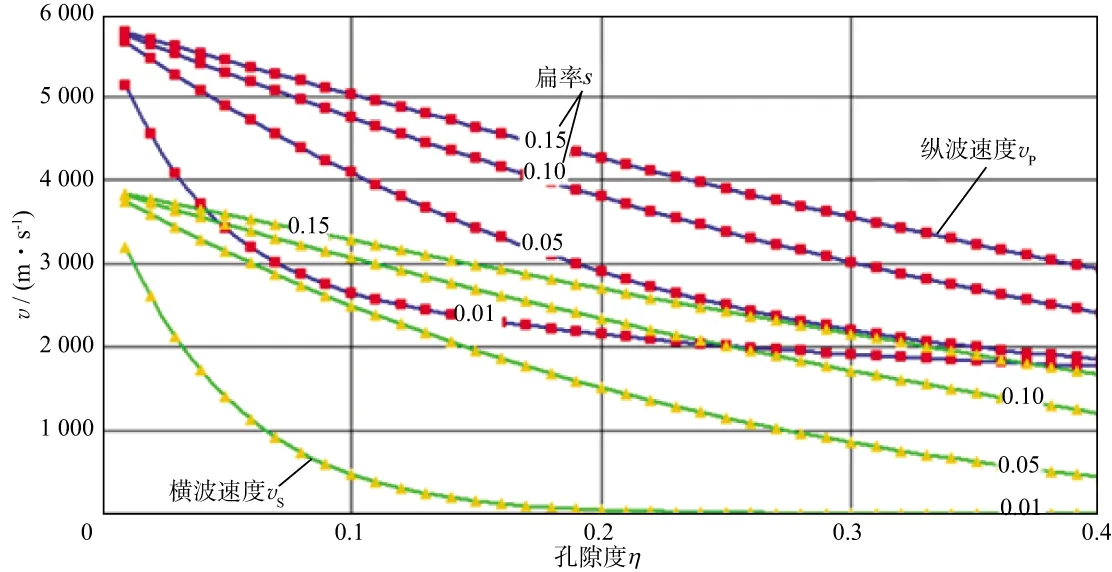
图3　基于Keys-Xu模型计算的孔隙度与地震速度交会分析结果

4　结束语

利用孔隙结构参数的数值化表示以及将岩石骨架统一模型引入Gassmann方程,我们获得了能够同时计算孔隙度和孔隙结构的扩展Gassmann方程。基于此方程,推导了饱和岩石弹性模量随孔隙度和孔隙结构等参数变化的简化公式,并对简化公式进行了适用性和精度分析,为定量解释和反演孔隙度和孔隙结构提供了可能。导出了全面评价和定量比较孔隙度和孔隙结构对储层弹性性质的影响因子R。根据R值的大小,得出3种基本情况:影响因子较大时,孔隙结构对饱和岩石有效压缩系数的影响起主要作用,孔隙结构引起的有效压缩系数的变化,可达一倍以上;影响因子较小时,孔隙度对饱和岩石有效压缩系数的影响起主要作用;影响因子适中时,二者的影响相当。作为对比,采用常见的Keys-Xu模型计算了储层纵、横波速度随孔隙结构和孔隙度的变化,经分析比较,无论是孔隙度还是孔隙结构均可使岩石的纵、横波速度的最大变化量达到2000～3000m/s,变化规律与所推导公式的结果一致。由于孔隙结构的复杂性,其丰富的内涵仍需在实践中继续挖掘。

[1]赵良孝,陈明江.论储层评价中的五性关系[J].天然气工业,2015,35(1):53-60

ZHAO L X,CHEN M J.A discussion on the relationships between five properties in reservoir evaluation[J].Natural Gas Industry,2015,35(1):53-60

[2]于豪,李劲松,晏信飞,等.非均质碳酸盐岩储层微观孔隙结构表征与气藏检测——以阿姆河右岸灰岩气藏为例[J].石油物探,2017,56(4):472-482

YU H,LI J S,YAN X F,et al.Microscopic pore structure characterization of heterogeneous carbonate reservoirs and the gas detection:a case study from limestone gas reservoirs on the right bank block of Amu Darya River[J].Geophysical Prospecting for Petroleum,2017,56(4):472-482

[3]SUN Y F,GOLDBERG D.Effects of aspect ratio changes on wave velocities in fractured rocks[J].Expanded Abstracts of 67thAnnual Internat SEG Mtg,1997:925-928

[4]李宏兵,张佳佳,姚逢昌.岩石的等效孔隙纵横比反演及其应用[J].地球物理学报,2013,56(2):608-615

LI H B,ZHANG J J,YAO F C.Inversion of effective pore aspect ratios for porous rocks and its applications[J].Chinese Journal of Geophysics,2013,56(2):608-615

[5]LIN K,XIAO X J,YANG X,et al.Self-adapting extraction of matrix mineral bulk modulus and verification of fluid substitution[J].Applied Geophysics,2011,8(2):110-116

[6]郭继亮,李宏兵,李明,等.一种体现孔隙形态影响的四参数孔隙度反演方法[J].石油物探,2016,55(4):576-586

GUO J L,LI H B,LI M,et al.Four parameters porosity inversion method representing the effect of pore morphology[J].Geophysical Prospecting for Petroleum,2016,55(4):576-586

[7]蔡涵鹏,贺振华,唐湘蓉,等.碳酸盐岩孔隙结构影响分析和等效孔隙结构参数计算[J].石油物探,2013,52(6):566-572

CAI H P,HE Z H,TANG X R,et al.Influence analysis of carbonate pore structure and calculation equivalent pore structure parameters[J].Geophysical Prospecting for Petroleum,2013,52(6):566-572

[8]ESHELBY J D.The determination of the elastic field of an ellipsoidal inclusion and related problems[J].Proceedings of the Royal Society A(Mathematical,Physical and Engineering Sciences),1957,241(1226):376-396

[9]WALSH J B.The effective of cracks on the compressibility of rock[J].Journal of Geophysical Research,1965,20(2):381-384

[10]MAVKO G,MUKERJI T,DVORKIN J.The rock physics handbook:tools for seismic in porous media[M].Cambridge:Cambridge University Press,2003:1-329

[11]JIANG L,WEN X T,ZHOU D H,et al.The constructing of pore structure model factor in carbonate rocks and the inversion of reservoir parameters[J].Applied Geophysics,2012,9(2):223-232

[12]PRIDE S R,BERRYMAN J G.Linear dynamics of double-porosity dual-permeability materials.I.governing equations and acoustic attenuation[J].Physical Review E,2003,68(3):036603

[13]NUR A.Critical porosity and the seismic velocities in rocks[J].EOS Transactions America Geophysical Union,1992,73(1):43-66

[14]刘曦翔,丁晓琪,王嘉,等.砂岩成分对储层孔隙结构及天然气富集程度的影响——以苏里格气田西区二叠系石盒子组8段为例[J].天然气工业,2016,36(7):27-32

LIU X X,DING X Q,WANG J,et al.Influence of sandstone composition on pore structures and gas enrichment degree:a case study on the 8thmember of Permian Shihezi Fm in the western Sulige Gas Field,Ordos Basin[J].Natural Gas Industry,2016,36(7):27-32

[15]肖忠祥,肖亮,张伟.利用毛管压力曲线计算砂岩渗透率的新方法[J].石油物探,2008,47(2):204-207

XIAO Z X,XIAO L,ZHANG W.A new method for calculating sandstone permeability by using capillary pressure curves[J].Geophysical Prospecting for Petroleum,2008,47(2):204-207

[16]HE X L,HE Z H,WANG X B,et al.Rock skeleton models and seismic porosity inversion[J].Applied Geophysics,2012,9(3):349-358

[17]GEERTSMA J,SMITH D C.Some aspects of elastic wave propagation in fluid-saturated porous solids[J].Geophysics,1961,26(2):169-181

[18]KEYS R G,XU S Y.An approximation for the Xu-White velocity model[J].Geophysics 2002,67(5):1406-1414

[19]KRIEF M,GARAT J,VENTRE J,et al.A petrophysical interpretation using the velocities of P and S waves (full-waveform sonic)[J].The Log Analyst,1990,31(6):355-369

[20]印兴耀,刘欣欣.储层地震岩石物理建模研究现状与进展[J].石油物探,2016,55(3):309-325

YIN X Y,LIU X X.Research status and progress of the seismic rock-physics modeling methods[J].Geophysical Prospecting for Petroleum,2016,55(3):309-325

[21]AVSETH P,MUKERJI T,MAVKO G.Quantitative seismic interpretation-applying rock physics tools to reduce interpretation risk[M].Cambrige:Cambrige University Press,2005:1-408

[22]陈颙,黄庭芳.岩石物理学[M].北京:北京大学出版社,2001:1-231

CHEN R,HUANG T F.Rock physics[M].Beijing:Peking University Press,2001:1-231

[23]RUSSELL B H,HEDLIN K.Fluid-property discrimination with AVO:a Biot-Gassman prospective[J].Geophysics,2003,68(1):29-39

[24]张佳佳,李宏兵,刘怀山,等.岩石物理建模中几种常见的骨架模型的精度分析[J].中国地球物理,2009:221-222

ZHANG J J,LI H B,LIU H S,et al.Accuracy analysis of dry frame models in rock physics modeling[J].The Chinese Geophysics,2009:221-222

[25]王炳章.地震岩石物理学及其应用研究[D].成都:成都理工大学,2008

WANG B Z.Seismic rock physics and its applied research[D].Chengdu:Chengdu University of Technology,2008

[26]熊晓军,贺锡雷,李翔,等.地震岩石物理学分析方法及应用实践[M].成都:四川科学技术出版社,2016:1-172

XIONG X J,HE X L,LI X.et al.Seismic rock physics analysis methods and applications[M].Chengdu:Sichuan Science and Technology Press,2016:1-172

附录A影响因子R的进一步推导

重写正文中的公式(12):

按此式求解饱和等效弹性参数βE。

将文中(13)式引入(12)式,得:

(A1)

对(A1)式整理后得:

(A2)

此式有两解,但βS/βE不能大于1,其值也不可为负。取其有物理意义的解:

(A3)

于是得:

(A4)

于是得:

(A7)

此结果与正文公式(17)完全一致。