一种基于隐私保护的作弊行为调查分析与估计方法

陈　明　彭慧丹　季春元　吴耀文

(湖北中医药高等专科学校　湖北　荆州：434020)

0　引言

考试作弊是一种常见社会现象，对这种行为需要进行一定程度的定量分析，这样有利用教学管理。但是作弊行为是一种敏感问题，如果要对这些行为进行调查，被调查者一般都会有所顾忌，即便采用无记名调查，被调查者很有可能回避或是故意做出错误回答，这样调查数据会失去很大程度上的真实性。因而设计一种调查方案，既能提高回答率又能降低虚假回答率显得十分必要。

本文提出的调查方案有两个基本出发点：首先，被调查者从是否作弊的若干问题中随机选择回答一个。其次，调查者也不知道被调查者回答的是哪个问题。这样既能保护被调查者个人隐私，又能让其对所选择问题真实回答。

1　作弊行为调查模型

1.1　作弊行为调查方案

首先准备若干张外形完全相同的卡片，每张卡片上印有1，2，3，…，m某一位数字，印有数字为k的卡片占总卡片的比例为PK(k=1，2，3，…，m)，且Pk不完全相同。接着被调查者随机抽取卡片一张，易知其抽到数字为k的概率为pK，若被调查者考试中有作弊行为，则回答m+1与其抽取数字之差；相反被调查者考试中没有作弊行为，则回答抽取的数字。

1.2　作弊行为调查分析

为便于数学分析，引入变量xi(i=1，2，3，…，n)并且设

设λ=P(xi=m+1)为被调查者的作弊概率。

设变量yi为第i名被调查者抽到卡片上的数字，易知yi(i=1，2，3，…，n)是独立同分布的且也与xi互相独立。

根据调查方案可知，第i名被调查者所回答的数字为ui=yi-xi，易知1≦ui≦m。

设nk为回答数字为k的人数(n1+n2+…+nm=n)，显然当ui=1，即回答数字为1时，由全概率公式可得

P(ui=1)=(1-λ)P1+λPm+1-1

(1)

推广可知，当ui=k，可得

P(ui=k)=(1-λ)Pk+λPm+1-k

(2)

则ui的数学期望为

(3)

E(ui)=λ(m+1-2E(yi))+E(yi)

(4)

进一步求ui的方差为

D(ui)=D(yi)+λ(1-λ)(m+1-2E(yi))2

(5)

(6)

(7)

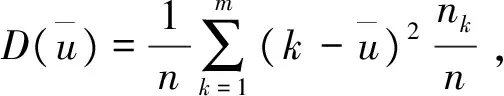
这里A是指该敏感问题(作弊行为调查)直接调查时产生的方差，B是指被调查者随机选取问题(卡片)产生的方差。

2　应用示例

假设被调查者总人数n=500，m=6，即卡片上数字k=1，2，…，6，相应占总卡片比例为

P1=0.5,P2=0.3,P3=0.1,P4=0.03,P5=0.04,P6=0.03。

被调查者回答数字1，2，…，6的人数分别是n1=196,n2=116,n3=50,n4=50,n5=48,n6=40。由此计算：

并代入式(6)与(7)，可知有作弊行为比例估计值

其相应的方差

若精度设为1倍标准差，则有作弊行为比例为19.25±2.33%；若精度设为2倍标准差，则有作弊行为比例为19.25±4.66%。

3　说明

[1]姜启源,谢金星,邢文训,等.大学数学实验[M].第二版.北京：清华大学出版社，2012.

[2]盛骤,谢式千,潘承毅.概率论与数理统计[M].第四版.北京：高等教育出版社，2008.

[3]彭秀云,闫在在.敏感问题调查设计以及估计[J].数学的实践与认识，2015，45(11):181-186.

[4]吴翠芳,曹维芳.敏感问题调查法在公安统计调查中的应用[J].廊坊师范学院学报(自然科学版),2015,15(3):16-19.

[5]Housila P. Singh,Tanveer A. Tarray. A dexterous randomized response model for estimating a rare sensitive attribute using Poisson distribution[J]. Statistics and Probability Letters,2014,90(7):42-45.

[6]彭秀云,闫在在.敏感问题问卷设计技术[J].应用数学学报,2009,32(1)：83-92.

[7]陈根龙.随机化回答技术在敏感性问题调查中的一种新应用[J].统计与决策,2007,(3)：23-24.

[8]蔡丹丰.影响大学生考试作弊行为的因素及干预策略[J].宁波大学学报,2016,38(5):83-86.