基于粗糙集理论修正的后续备件指数平滑预测方法

董骁雄, 陈云翔, 蔡忠义, 张玮玉

(1. 空军工程大学装备管理与安全工程学院, 陕西 西安 710051; 2.中国南方航空股份有限公司西安分公司, 陕西 西安 710065)

0　引　言

后续备件,是指装备在保证期以后所规定的时间内为恢复装备的设计性能所必需的可修复件和不可修复件,以满足使用方各级维修所需的备件为主,包括替换故障的周转备件[1]。在装备的保障资源中,备件对装备完好率的影响是最直接、最敏感的,而备件系统大量订货和管理的是后续备件,因此对后续备件需求预测具有重要的军事和经济研究价值。

后续备件一般已积累了一定数量的实际使用数据,具有丰富的历史故障信息,可以根据备件消耗的历史资料推测未来维修备件的需求量。国内外学者对后续备件需求预测的研究已经取得一定成果,主要体现在预测方法的多元化,有统计分析法、回归分析法、时间序列法、人工神经网络法、灰色预测法等[2-10],这些方法以探究备件需求本身的发展规律为思想进行预测,当数据坡度大、预测周期过长或者系统受外部干扰强烈时,通过传统模型很难得到满意的效果,得到的预测结果通常误差较大。鉴于备件需求预测基本方法的局限,国内外学者开展了对备件需求预测方法的改进研究工作,比如采用改进动态自适应隔代映射遗传算法和阻尼最小二乘法优化的自回归滑动平均模型(auto-regressive and moving average model,ARMA)模型进行预测备件需求[11],又如借鉴物理力学中的矢量合成方法优化回归模型预测备件需求[12]。这些方法大多针对某一基本预测方法的内部缺陷进行改进,这些改进只针对方法本身,而忽视了装备在使用过程中影响备件需求数据波动的因素且缺乏通用性,当与不同的基本预测方法组合使用时,由于各自特性差异会产生新的问题,例如不同预测方法之间的兼容性问题以及组合预测方法的优越性问题。

针对上述情况,从区别于传统备件需求预测改进研究的新视角出发,提出一种不依赖于基本预测方法的基于粗糙集理论修正的备件需求预测改进方法,以指数平滑法作为基本预测方法进行分析验证,通过算例对比分析证明,本文提出的方法可以有效提高备件需求预测精度,从装备使用层面上实现了对备件需求基本预测方法的改进,且因为无需引入其他辅助方法而通用性较强。

1　基于指数平滑法的后续备件预测

1.1　方法原理

指数平滑法最早由美国学者布朗提出[13],其实际上是一种特殊的加权移动平均法,其特点在于:对离预测期最近的观察值,给与最大的权数,而对离预测期渐远的观察值给予递减的权数;运用指数平滑法预测后续备件需求,依照“近大远小”的原则,赋予观测值不同的权重,既充分利用了历史各期观测值的信息,又突出了近期数据的影响,能够及时跟踪反映备件需求量的最新变化[14]。

设备件需求量时间序列为y1,y2,…,yt,则单次、二次、三次指数平滑法模型分别为

(1)

式中,yt为第t年的备件需求量;α为平滑系数,0≤α≤1。

三次指数平滑法的预测模型为

(2)

指数平滑法是一个迭代计算的过程,需要先估算初始值s0,1,当时间序列数量超过20个时,初始值对结果影响较小,可以令s0,1=y1,当时间序列数量不足20个时,可取前几个观测值的平均值代替。

指数平滑法中的平滑系数α是一个可调节的权重值。α的选择是指数平滑法的关键,一般可以从以下几个方面考虑[15]:

(1) 若时间序列中随机波动成分较大,为了尽可能消除随机波动的影响,可选择较小的α;反之若随机波动成分较小,为了及时跟踪需求的变化,突出新数据的影响,可选择较大的α。

(2) 若备件需求趋势的变化很平缓,可选择较小的α,取值可在0.05～0.2;若备件需求有波动,但长期趋势变化不大时,可选稍大的α值, 取值可在0.1～0.4;若备件需求波动很大,长期趋势变化幅度较大,呈现明显且迅速的上升或下降趋势时,宜选择较大的α值,取值可在0.6～0.8,以使预测模型灵敏度更高,能迅速跟上数据的变化;当备件需求量是上升(下降)的发展趋势类型,α应取较大的值,在0.6～1。

(3) 一般应用过程中,也可通过选择大小不同的α进行试算,预测误差最小的α值就是最佳平滑系数。

1.2　预测实例分析

假设空军某部队2001-2015年某飞机发动机备件的需求资料如表1所示。现根据表1中的数据运用指数平滑法来测算备件需求量。

表1　空军某部队2001-2015年某航空备件的需求数据

不同次数的指数平滑法适用范围不同,当时间序列呈线性趋势时,宜采用一次、二次指数平滑法,当时间序列呈非线性趋势时,可用三次指数平滑法。应用Matlab软件对表1中2001-2013年备件需求数据进行拟合,结果呈现二次曲线趋势的拟合程度较高,如图1所示。因此,采用三次指数平滑法建立模型,可以更好地反映备件需求变化趋势。

图1　备件需求量拟合曲线

根据式(2)可得

可得

由式(2)可得s0,1、s0,2、s0,3分别为

(3)

由于备件需求量呈上升的发展趋势类型,α应取较大的值,经过试算,取α=0.60,可得

根据式(1),应用Matlab软件计算得到2001-2013年备件需求量一次、二次、三次指数平滑值,并代入式(2)得到

则线性预测方程为

(4)

根据式(4)预测2014-2015年备件需求量,并与实际备件需求量进行对比,如表2所示。

表2　预测结果与实际值对比

由预测结果可见,误差超过5%,预测精度有待进一步提高。

2　基于粗糙集理论的修正模型

2.1　指数平滑模型的缺点

运用指数平滑法对备件需求进行预测时,若数据序列坡度大,预测区间过长或系统外部环境变化巨大,则该方法预测效果不是很理想,得到的预测结果误差较大。因此需要对结果进行修正,提高预测精度。

从指数平滑预测模型能够看出,预测值是一个通过累加和累减生成的序列,在装备使用相对稳定的情形下,该预测结果预测精度较高,但是通常情况下,装备任务需求、使用环境、保障能力要求和维修水平等因素都一直处于动态变化之中,造成装备实际备件需求量随这些相关因素的波动而改变,所以在实际的备件需求预测中,必须要考虑预测周期内备件需求影响因素的变化,以此为依据修正预测结果,进一步提高预测精度。

2.2　粗糙集修正模型

在预测结果中加入修正因子a,得到修正值为

(5)

式中,Δx指装备入役期间的备件年度需求量最大值和最小值之差,表示为

(6)

2.2.1备件需求影响因素分析

备件是装备维修的重要物质基础,是快速恢复装备完好率和装备作战能力的先决条件。因此,备件需求源于部队的任务需求,但同时也受到使用环境、保障能力要求及维修水平等因素的影响[10]。

(1) 任务需求

任务需求表现为装备执行任务过程中需要的备件品种和数量。任务需求是影响备件需求的重要因素,对备件需求起着拉动式的作用。部队每年不仅需要完成例行的日常训练任务,还需要根据上级安排执行打靶、演习等外出任务。不同的任务,需要完成的训练科目、参与的装备数量、装备的出动强度、工作时间都不尽相同,因此备件需求也不相同。一般情况下,参与的装备数量越多、装备的出动强度越大、工作时间越长,对备件的需求越大。

(2) 使用环境

使用环境是指装备在执行任务过程中的工作环境,不同的任务,装备使用环境都不尽相同,因此备件需求也不相同,一般情况下,装备的使用环境越恶劣,对备件的需求越大。

(3) 保障能力要求

保障能力要求是指在某一时期内备件保障所要达到的目标和水平,衡量保障效能的常用指标是备件保障概率。备件保障概率是指当需要备件时,备件需求被满足的概率。备件保障概率的要求越高,备件需求就越大。

(4) 维修水平

装备维修水平随着维修人员流动会发生改变,维修水平对于可修件的影响表现为备件修复概率,对于不可修件的影响表现为维护时的拆装损耗。

2.2.2指标的规范化

(1) 对备件需求影响因素进行评定,得到样本数据

任务需求以装备工作小时记录,同时考虑到日常训练任务备件需求量和执行外出任务备件携行量。

使用环境参考执行任务地区气象股的观测数据,将其量化为7个等级,数值越大表示环境越恶劣。

保障能力要求根据执行任务性质的不同将其量化为7个等级,数值越小表示保障能力要求越高。

维修水平根据保障单位的实际情况将其量化为7个等级,数值越小表示维修水平越高。

(2) 备件需求影响因素的样本值规范化处理

备件需求影响因素中属于效益型指标的是任务需求,属于成本型指标的是使用环境、保障能力和维修水平。将各项因素对应年度的量化值记为Cij,其中,i=1,2,3,4；j代表年度。通过波动比例bij来表示各影响因素的年度波动情况。

对于正极性(效益型)定量指标,目标效果样本值越大越好,表示为

(7)

对于负极性(成本型)定量指标,目标效果样本值越小越好,表示为

(8)

2.2.3备件需求影响因素权重确定

确定备件需求影响因素的多属性决策中,各属性都具有偏好信息,装备的任务需求、使用环境、保障能力要求及维修水平随着装备使用计划、军队使命任务等因素的波动动态变化,情况不易掌握,属性有时未知,因此,备件需求影响因素的确定是一个不完备的信息系统。

定义1[16]S=(U,A,V,f),其中,U为对象的非空有限集合;A=C∪D为属性的非空有限集合;C为条件属性的非空有限集;D为决策属性的非空有限集合;V是A的属性值集合,Va是属性a∈A的值域,Va可以为实数值的连续型数据也可以为语言描述型数据;f是信息函数,f:U×A→V,即f(x,a)∈Vaf,表示指定U中每一个对象x的属性值。若S中至少有一个属性a∈A,使Va含有空值(*),则称S是一个不完备信息系统。

定义2给定信息系统S=(U,A,V,f),文献[15]给出“相容关系”定义[17]。∀φ⊂P⊆A确定了U上的一个二元关系TP，即

TP(x,y)⟺∀a∈P,f(x,a)=f(y,a)∨

f(x,a)=*∨f(y,a)=*x,y∈U

(9)

显然TP满足自反性和对称性,称TP是由P确定的U上的一个相容关系。简记由属性a∈A确定的相容关系Ta。

定义3给定信息系统S=(U,A,V,f),U={x1,x2,…,x|U|},B⊆C的信息量定义[18-19]为

(10)

式中,|X|表示集合X的基数。

由性质1知,若通过属性集B可以划分U中的每个对象,则B所提供的信息量最大;若B无法划分U中任意两个对象,则B所提供的信息量为零。

定义4对不完备信息系统S=(U,C,V,f),定义属性b∈B⊆C在属性集B中的重要度为

SigB{b}(b)=I(B)-I(B{b})

(11)

定义2表明,属性集B中的属性b在B中的重要性由去掉该属性引起的信息量变化程度进行度量。特别地,单个属性的重要性Sigφ(b)=Sig(b)=I({b}),b在B中的权重通过重要度归一化后确定,即

(12)

2.2.4修正因子计算方法

由综合备件需求影响因素的权重W和波动比例Bj=[b1j,b2j,b3j,b4j]T,年度修正因子aj可表示为

aj=WBj

(13)

式中,W为各影响因素对备件需求波动的影响权重,表示为

W=[W1,W2,W3,W4]

(14)

通过式(13)计算得到修正因子aj,将结果代入式(5),就能得出备件需求量的修正值。

3　算例分析

设某装备入役若干年,得到备件需求影响因素的属性值决策表,如表3所示(部分属性值未知)。根据第2.2.1节中的分析,影响备件需求的因素主要有任务需求、使用环境、保障能力要求和维修水平,因此,有4个条件属性b={b1,b2,b3,b4}和1个决策属性d。各属性值为b1={大,中,小}={2,1,0},b2={好,中,差}={2,1,0},b3={高,低}={1,0},b4={高,中,低}={2,1,0};d={多,一般,少}={2,1,0}。

表3　备件需求量决策表

根据式(9)～式(12)求得b各备件需求影响因素权重为

I(B)=0.84

SigB(b1)=I(B)-I(B{b1})=0.08

SigB(b2)=I(B)-I(B{b2})=0.03

SigB(b3)=I(B)-I(B{b3})=0.04

SigB(b4)=I(B)-I(B{b4})=0.03

w(b1)=0.44,w(b2)=0.17

w(b3)=0.22,w(b4)=0.17

根据第2.2.2节针对该飞机发动机备件,通过调研，有针对性地取得了备件需求影响因素的年度相关数据,如表4所示。

表4　备件需求影响因素量化值

根据式(7)和式(8)对表3中指标进行规范化处理,结合权重W=[0.44,0.17,0.22,0.17]T,代入式(13),得出各年度修正因子为

a=[-0.007 70.023 10.038 50.030 80.007 7 -0.030 7-0.015 4-0.030 7-0.046 2-0.023 1 -0.061 5-0.023 1-0.061 50.053 80.092 3]

将修正因子代入式(5)计算得到修正后的备件需求预测值,如表5所示。将本文所述预测模型与指数平滑法的预测结果进行对比,如图2所示。

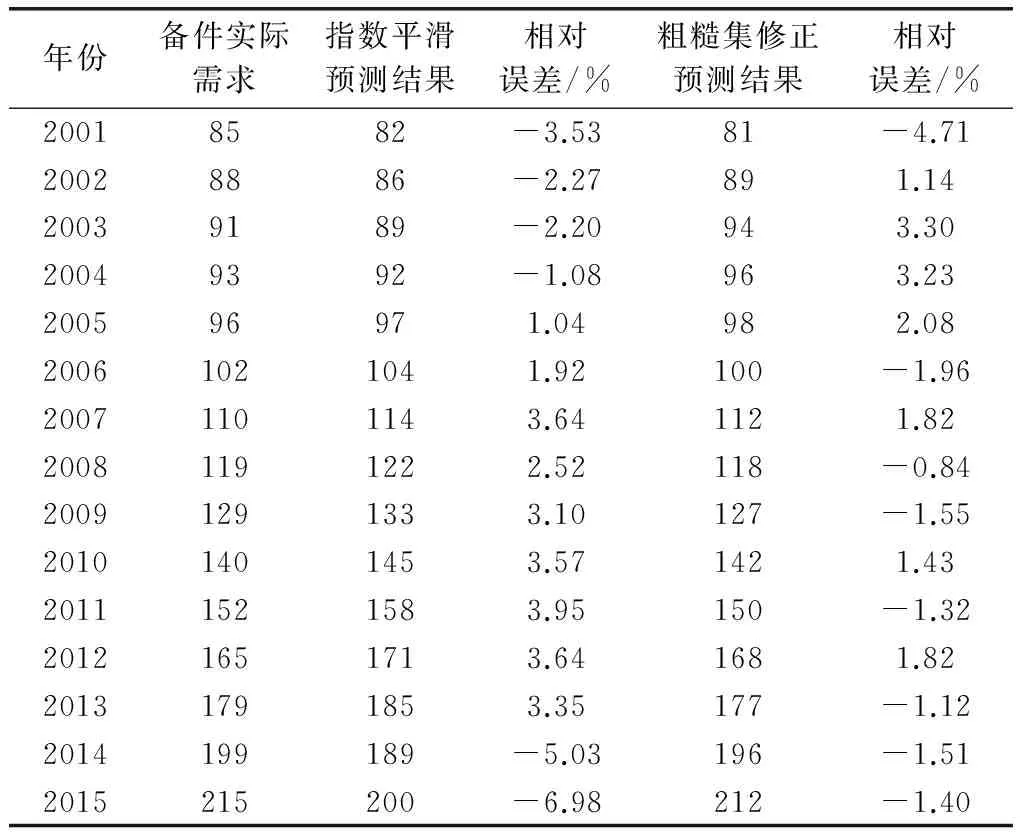
表5　预测结果对比

图2　预测结果对比图

由表5和图2可以看出,指数平滑法的最大预测误差为6.98%,累计预测误差达到47.82%;经过粗糙集修正后的最大预测误差为4.71%,累计预测误差为29.23%;预测结果的准确性显著提高,尤其对于最近两年的备件需求预测,准确率极高,体现了修正模型的优越性。

4　结　论

本文从装备在使用过程中影响备件需求数据波动的因素出发,对后续备件需求预测方法进行改进,并以指数平滑法作为基本预测方法进行算例分析,对本文提出的改进方法的通用性进行验证,计算结果表明,本文提出的改进方法虽然没有从某一基本方法的内部特性出发进行改进,但也可以显著提高备件需求预测精度,且正是因为不依赖于某一基本预测方法的具体特性局限,所以本文提出的改进方法通用性更强。

误差修正是备件需求预测的一个新思路,在应用过程中,该方法还存在依赖装备使用数据的准确性、装备使用和备件需求之间复杂映射关系确定困难等缺点,有待进一步分析和研究,建立完善的备件需求预测误差修正体系,提高备件需求预测精度。

参考文献：

[1] 全军军事术语管理委员会. 中国人民解放军军语[M]. 北京: 军事科学出版社, 2011.

Army military terminology management committee. The Chinese people’s liberation army troops[M]. Beijing: Military Science Press,2011.

[2] JOSE R, MARCO A M. Demand forecasting and inventory control: a simulation study on automotive spare parts[J]. International Journal of Production Economics, 2015, 161(1): 1-16.

[3] ROSIENKIEWICZ M, CHLEBUS E, DETYNA J. A hybrid spares demand forecasting method dedicated to mining industry[J]. Applied Mathematical Modelling, 2017, 49(21): 87-107.

[4] GUO F, DIAO J, ZHAO Q H, et al. A double-level combination approach for demand forecasting of repairable airplane spare parts based on turnover data[J]. Computers & Industrial Engineering, 2017, 110(5): 92-118.

[5] ZHU Q, LIU S Y, HUANG Z J, et al. Prediction model of spare parts consumption based on engineering analysis method[J]. Procedia Engineering, 2017, 174(12): 711-716.

[6] ZHU S, DEKKER R, JAARSVELD W V, et al. An improved method for forecasting spare parts demand using extreme value theory[J].European Journal of Operational Research,2017,261(1): 169-181.

[7] KIM T Y, DEKKER R, HEIJ C. Spare part demand forecasting for consumer goods using installed base information[J]. Computers & Industrial Engineering, 2017, 103(6): 201-215.

[8] SI X S, ZHANG Z X, HU C H. An adaptive spare parts demand forecasting method based on degradation modeling[M]. Berlin: Springer, 2017: 405-417.

[9] HEMEIMAT R, AL-QATAWNEH L, ARAFEH M, et al. Forecasting spare parts demand using statistical analysis[J]. American Journal of Operations Research, 2016, 6(2): 8-12.

[10] BERGMAN J J, NOBLE J S, MCGARVEY R G, et al. A Bayesian approach to demand forecasting for new equipment programs[J].Robotics and Computer Integrated Manufacturing, 2016,47(10): 17-21.

[11] 赵建忠, 徐廷学, 李海军, 等. 基于小波分析的导弹装备备件需求组合预测[J]. 电子学报, 2014, 42(3): 417-423.

ZHAO J Z, XU T X, LI H J, et al. Combination forecasting of missile equipment spare parts demand based on wavelet analysis[J]. Acta Electronica Sinica, 2014, 42(3): 417-423.

[12] 林琳, 陈湘芝, 钟诗胜. 基于特征合成的周期性备件需求预测方法[J]. 哈尔滨工业大学学报, 2016, 48(7): 28-32.

LIN L, CHEN X Z, ZHONG S S. Demand forecasting method for periodic spare parts based on feature synthesis[J]. Journal of Harbin Institute of Technology, 2016, 48(7): 28-32.

[13] SIREGAR B, BUTAR-BUTAR I A, RAHMAT R F, et al. Comparison of exponential smoothing methods in forecasting palm oil real production[J]. Journal of Physics: Conference Series, 2017, 801(1): 1-12.

[15] LIU X C, ZHANG Y L, HUANG A J, et al. Requirement forecasting of equipment’s maintenance spares-parts based on exponential smoothing method[J]. Advanced Materials Research, 2013, 605(12): 9-13.

[16] LIANG J Y, XU Z B. The algorithm on knowledge reduction in incomplete information systems[J]. International Journal of Uncertainty, Fuzziness and Knowledge-based Systems, 2002, 10(1): 95-103.

[17] KRYSCKIEWICZ M. Rough set approach to incomplete information system[J].Information Sciences,1998,112(1/4):39-49.

[18] GUAN J W, BELL D A, GUAN Z. Matrix computation for information systems[J].Information Sciences,2001,131(1/4):129-156.

[19] HU Q W, SALEM C, SAJID S, et al. Spare parts classification in industrial manufacturing using the dominance-based rough set approach[J]. European Journal of Operational Research, 2017, 262(3): 1136-1163.