基于ADS-B的多站时间同步系统的偏差联合估计方法

马永圣, 张　敏, 郭福成

(国防科技大学电子科学学院, 湖南 长沙 410073)

0　引　言

在多站时差定位系统中,主要通过中心站测量和分布式测量两种方式测量信号到达时间差,其中分布式测量法施工难度小、成本低,应用更广泛[1-5]。分布式测量法需要精确的站间时间同步,否则将引起慢时变的定位误差[6-8]。目前基于全球定位系统(global positioning system,GPS)、北斗等导航卫星共视实现站间同步的方法,同步精度一般为几十纳秒[9-10],需要增加双向数据链提高精度[11-12]。通过增加地面标校站进行站间同步的方法,往往需要多个标校站解决共视问题[6],但多个标校站也需要进行时间同步,系统复杂、成本高且隐蔽性差[13]。文献[3]提出利用飞机当前位置的测量值进行同步,但观测站数量必须多于待同步站的数量,且需要多架飞机。由于飞机发射的广播式自动相关监视(automatic dependent surveillance-broadcast,ADS-B)信号中包含飞机位置、速度和航向等信息[14-15],因此,安装ADS-B系统的飞机可以作为已知位置的移动标校站对观测站进行时间同步[16]。基于ADS-B的多站时间同步系统受ADS-B位置误差的影响,其中系统延时误差影响最大[16-17]。系统延时误差是机载导航设备完成对飞机定位到ADS-B消息发射的时间延迟引起的飞机位移,必须对其准确估计,以消除对同步精度的影响。

针对这一问题,文献[18]利用ADS-B跟踪滤波结果和雷达测量数据融合的方法,估计和消除系统低频误差,但该方法要求雷达具备高精度测量能力,并且需要进一步消除雷达测量偏差,同时ADS-B滤波过程也会引入误差,整体系统复杂。文献[19]提出一种基于辅助源和相关熵的ADS-B信息时延估计算法,引入相关熵分析ADS-B信号和辅助源信号的多普勒频移相似性,从而估计时延误差,但该方法利用了飞机对辅助源信号的散射,广义信噪比在35 dB以下时,估计误差已达几百毫秒,且该方法需要建立辅助源,无源性差。文献[20]提出一种精确计算每个ADS-B报文延迟时间的方法,但该方法每隔一段时间将位置测量时刻加载到报文中,需要改变现有报文格式,实用性较差。文献[21]分析了ADS-B时间延迟对ADS-B/广域多点定位(wide area multilateration,WAM)数据关联跟踪精度的影响,存在延迟误差时,概率数据关联(probability data association,PDA)方法的跟踪误差和稳健性均优于最近邻数据关联(nearest neighbor data association,NNDA)方法,但没有提出减小估计误差、提高跟踪精度的方法。文献[16]提出一种航迹相消的方法消除ADS-B延时误差,运用同一架飞机正向和反向飞过的两段航迹进行站间时间同步,但该方法受两段航迹重合度的影响,且正反对应的两段航迹不易获得。

基于各项系统误差对同步精度影响的分析,为消除影响较大的系统延时误差,本文提出一种延时误差和待同步站钟差联合估计的方法,估计性能可以达到克拉美-罗下限(Cramer-Rao lower bound,CRLB),大大提高了基于ADS-B的多站时间同步系统的同步精度。

1　同步模型

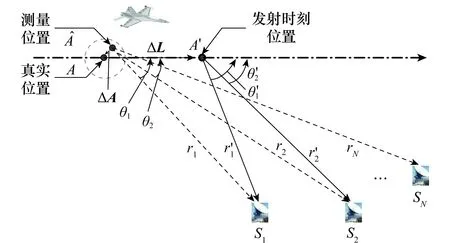
图1　基于ADS-B的多站时间同步模型

ADS-B的位置误差包括固定误差和随机误差,其中固定误差由延时误差引入,随机误差由定位误差和数据链误差引入[14]。设飞机的ADS-B位置误差向量为Ψ,则

Ψ=ΔL+ΔA

(1)

设飞机飞行的方位角为α,俯仰角为β,那么ADS-B位置误差向量Ψ可以进一步分解到x、y、z方向,即

(2)

式中,ΔL=‖ΔL‖;ξx、ξy、ξz分别为ADS-B位置误差的随机误差分量。

(3)

式中,bxq,yq,zq表示各站站址偏差;ξxq,yq,zq表示各站站址随机误差分量。

(4)

(5)

多站定位系统测量时差时，只需将时间同步到同一基准,并不一定是UTC时间,因此可以选择同步到基准站S1。那么各站与基准站的时钟差为

(6)

式中,ξΔti(i=2,3,…,N)表示时差测量随机误差。利用各站与基准站的钟差修正各站时钟，即可完成多站时间同步。

通过上述建模分析可知,基于ADS-B的多站时间同步系统的系统误差主要包括固定偏差和随机误差两部分,其中，固定偏差可以分为3类:ADS-B位置的偏差(即系统延时误差)、待同步站钟差和站址测量偏差。随机误差也可以分为3类:ADS-B位置的随机误差、站址测量随机误差和时差测量随机误差。固定偏差是恒定的未知参量,可以进行联合估计。分析各类误差对时间同步精度的影响,对同步精度影响较小的偏差量可以忽略不计,仅对其余偏差量进行联合估计。

2　同步精度分析

(7)

令

Δt=[t2-t1,t3-t1,…,tN-t1]T,

Ξ0=[ξΔt2,ξΔt3,…,ξΔtN]T

将式(7)写为矩阵形式，即

(8)

那么各系统偏差等效成的时差随机误差的协方差矩阵为

(9)

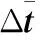
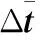
(10)

式中,axi=γi-γ1,其中

(11)

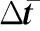
(12)

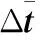
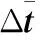
(13)

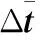
由于时差是根据各站与基准站作时间差求得,包含测时误差等共同误差因素,因此时差测量的随机误差ξΔti之间是彼此相关的,那么

(14)

式中,ηij表示ξΔti和ξΔtj之间的相关系数。

考虑到

(15)

式中,IN-1表示N-1阶单位阵;QN-1表示N-1阶全1矩阵。

因此,式(9)可以化简为

Pf=[ζij],i,j=2,3,…,N

(16)

式中

(17)

那么由随机误差引起的各站与基准站的同步误差的方差为D(Pf),其中D(Pf)表示方阵Pf的主对角线元素构成的列矢量。

各偏差量等效成的时差偏差为

bΔt=HAΔL+D(Hxi)bxi+D(Hyi)byi+

D(Hzi)bzi+Hx1bx1+Hy1by1+Hz1bz1

(18)

因此,总的同步误差均方差为

(19)

ADS-B位置报文中使用导航完整性等级(navigation integrity category,NIC)表征水平位置的误差信息[25-26],采用1 090 MHz扩展断续震荡(extended squitter,ES)数据链的ADS-B消息的NIC小于9,实际中70%以上等于7[16]。全部系统延时小于1.5 s的概率为95%,其中不可补偿延时小于0.6 s(95%),那么飞机速度为250 m/s时,系统不可补偿延时引起的位置误差达到150 m[21, 27]。另外,NIC为7时,ADS-B位置误差的随机误差标准差大致为10 m。站址测量误差(参考美军军用GPS)为0.5 m[16]。

仿真场景:四站星型布站,主站和各辅站的间距均为15 km,位置分别为(0,0,0)km、(0,15,0)km、(-12.99,-7.5,0)km、(12.99,-7.5,0)km;设主站和辅站1的钟差ΔTi1=100 ns,时差测量的随机误差为10 ns,飞机飞行的方位角α=45°,俯仰角β=2°,系统延时0.6 s,飞机速度250 m/s,初始高度8.8 km,ADS-B位置的随机误差为10 m,主站和辅站1的站址测量误差的偏差分量为bx=by=bz=0.5 m,其随机误差分量均为0.1 m。

容易分析得到时差测量的随机误差引起的同步误差为10 ns。选取不同起始位置的航迹进行同步时,ADS-B位置误差和站址测量误差引起的主站和辅站1的同步误差分布如图2所示。

图2　主站和辅站1的同步精度分布图

从图2中可以看出,系统延时引起的ADS-B位置偏差对时间同步的影响最大,图示范围内两站时间同步的均方根误差的最大值为458.65 ns,最小值为0.001 7 ns;飞机在观测站附近空域飞行时,ADS-B位置的随机误差对时间同步的影响较大,图示范围内两站时间同步的均方根误差的最大值为30.59 ns,最小值为0.000 1 ns;站址测量误差对时间同步的影响相对小得多,在图示范围内均小于5 ns,可不进行考虑。

ADS-B位置的随机误差引起的同步误差相比ADS-B位置偏差引起的同步误差要小很多,且各项随机误差均服从正态分布,具有零均值特性,可以通过对多次数据处理结果求平均,以减小随机误差的影响。因此,本文对系统延时误差和待同步站钟差进行联合估计,消除其引起的时间同步误差。

3　延时误差与待同步站钟差联合估计方法

式(7)所示观测方程可以简化为

(20)

式中

(21)

tin-t1n=Δtin+ξΔtin

(22)

(23)

假设Ξ～Ν(0,C),估计参数矢量为θ=[ΔLΔT]T,则似然函数[28]为

(24)

那么

(25)

式中,J(θ)表示代价函数。

假设观测时间内系统延时误差和待同步站钟差为不变常量[28],采用高斯-牛顿迭代算法计算,主要步骤如下:

步骤2迭代计算。

步骤2.1开始迭代,k=1;

(26)

那么修正项

(27)

更新估计值

(28)

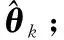
4　CRLB计算

根据式(24)和式(26)计算Fisher信息阵[30]为

(29)

假设各次观测是独立的,且ξΔtin～Ν(0,σ2),则式(29)可以化简为

(30)

那么CRLB为

CRLB=σ2(HTH)-1

(31)

5　仿真分析

5.1　航向对同步精度的影响

5.1.1未消除系统延时误差的场景

根据第2节的理论分析,作为主要的系统偏差项,延时误差引起的同步误差的大小与飞机航向有关,下面通过仿真验证系统延时误差未消除条件下飞机航向对同步精度的影响,以下仿真结果为系统延时误差引起的同步误差(见图3和图4)。

场景1飞机飞行的方位角α=0°,俯仰角β=2°,其余仿真场景的设定与第2节一致。

图3　未消除偏差时主站和辅站1的同步精度分布图(α=0°,β=2°)

场景2飞机飞行的方位角α=0°,俯仰角β=45°,其余仿真场景的设定与第2节一致。

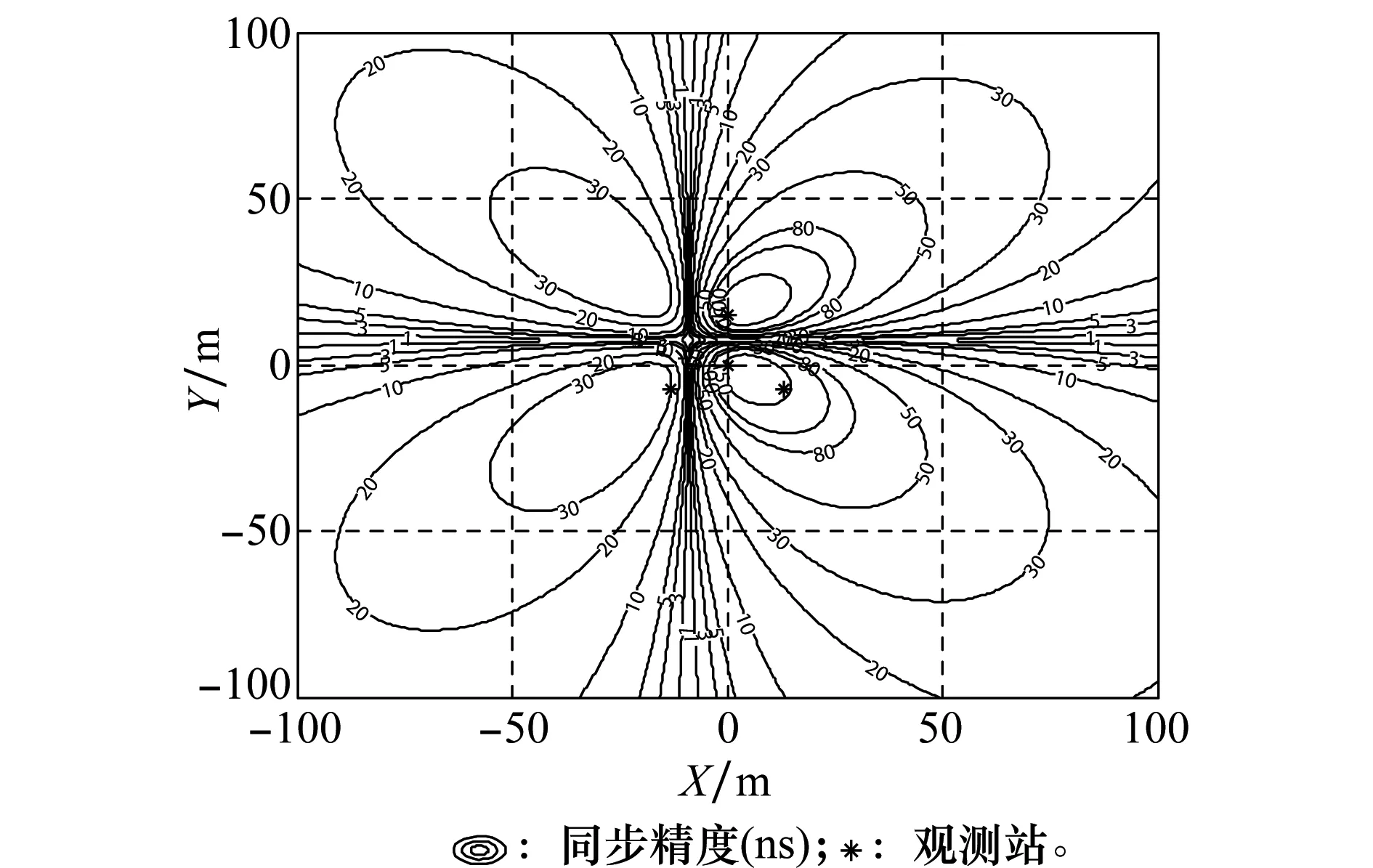
图4　未消除偏差时主站和辅站1的同步精度分布图(α=0°,β=45°)

综合比较图2～图4,可以看出:选取不同航向的飞机进行同步时,同步精度分布的差异较大,这主要是由于不同航向、不同位置飞机的延时误差对测量时差的影响程度不同。在不同场景下,选取沿主站和辅站1时差线方向运动的飞机或者主站和辅站1连线方向空域的飞机进行同步时,同步误差较小,这是因为飞机处于这些空域飞行时,信号到达两个站的时间差基本恒定,系统延时误差对时差测量值几乎没有影响。实际中飞机稳定飞行时俯仰角接近0°,选择沿主站和待同步辅站时差线方向飞行或两站连线方向空域的飞机,在不进行偏差消除的情况下也可以达到较高的同步精度。

5.1.2联合估计并消除系统偏差的场景

利用本文算法对延时误差和待同步站钟差进行联合估计,并予以消除,下面通过仿真验证系统偏差消除后飞机航向对同步精度的影响(见图5和图6)。

场景1仿真场景的设定与第2节一致,观测时长100 s。

图5　消除偏差后主站和辅站1的同步精度分布图(α=45°,β=2°)

场景2飞机飞行的方位角α=0°,俯仰角β=2°,观测时长100 s,其余仿真场景的设定与第2节一致。

图6　消除偏差后主站和辅站1的同步精度分布图(α=0°,β=2°)

比较图5和图6,可以验证飞机航向会影响本文方法的同步精度。通过比较图2(a)和图5,图3和图6,可以看出:在图示范围内,选取大部分探测区域的飞机对主站和辅站1进行同步时,本文方法显著提高了同步精度,但也有部分区域由于观测性较差引起较大的同步误差,主要是由于飞机沿时差线方向运动时,两站的测量时差基本不变,使得系统延时误差不可估计,而根据第5.1.1节的结论,飞机沿时差线方向运动时,不进行偏差消除即可达到较高的同步精度。因此,为了保证较高的同步精度,当有多架次飞机可供选择时,应避免选用观测性较差空域的飞机,当仅在这些观测性差的区域探测到飞机时,对偏差消除前后的同步精度进行比较,选择最佳的同步方案,也可以通过增大观测间隔和累积观测时间,提高联合估计方法的同步精度。

5.2　联合估计算法的性能

仿真场景的设定与第2节一致,飞机初始位置坐标为(10,10,8.8)km,观测时间内飞机始终处于观测站共视范围内,ADS-B空中位置消息的广播速率为2 Hz。系统延时误差的初值可以在m至km量级的较大范围内随机选取,而观测站钟差的初值可以在ns至ms量级的较大范围内随机选取,高斯-牛顿迭代算法的最大迭代次数为5次。

估计量的均方根误差(root mean square error,RMSE)为

(32)

观测时间分别设定为10 s、60 s、100 s,进行10 000次蒙特卡罗仿真,比较本文方法对系统延时误差和待同步站钟差的估计误差均方根RMSE和CRLB,如表1所示。

表1　不同观测时长下的联合估计性能

从表1可以看出,本文方法可以准确估计出系统延时误差和待同步站钟差,同时均方根误差接近CRLB;观测时间较短时,CRLB较大,随观测时间增加,算法性能提高。

为分析本文方法对于同步精度的提高作用,统计观测时长不同时对应的系统偏差消除前后的同步精度,如表2所示。

表2　系统偏差消除前后的同步精度

从表2可以看出,本文方法可以明显提升同步精度,随着累积观测时间的增加,同步精度可以达到5 ns以内。

6　结束语

为了消除基于ADS-B的多站时间同步系统的系统偏差引起的同步误差,本文建立了偏差条件下基于ADS-B信号的多站同步模型,通过对各项偏差引起的同步误差的分析,指出对同步精度影响最显著的系统延时误差,对此提出了一种ADS-B延时误差和待同步站钟差联合估计方法。仿真分析表明:选取不同航向的飞机进行同步时,系统偏差消除前后同步精度分布的差异均较大,选取观测性较好的空域的飞机,可以达到更高的同步精度;本文算法可以准确估计出系统延时误差和待同步站钟差,估计的均方根误差接近CRLB,且观测时间越长,估计性能越好,显著提高了多站时间同步精度。

参考文献：

[1] HUANG B Q,XIE L H,YANG Z. TDOA-based source localization with distance-dependent noises[J]. IEEE Trans.on Wireless Communications,2015,14(1):468-480.

[2] KAY S,VANKAYALAPATI N. Improvement of TDOA position fixing using the likelihood curvature[J]. IEEE Trans.on Signal Processing,2013,61(8):1910-1914.

[3] GALATI G,LEONARDI M,MAGARO P,et al. Wide area surveillance using SSR mode S multilateration:advantages and limitations[C]∥Proc.of the European Radar Conference,2005:225-229.

[4] MANDLIK M,NEMEC Z. An accurate time-difference measurement method for passive radar applications[C]∥Proc.of the 23rd International Conference Radioelektronika,2013:406-409.

[5] SANG V,VESELY J,JANU P. The measure-ment of TDOA short baseline[C]∥Proc.of the International Conference on Military Technologies,2015:1-5.

[6] VELA G,PORTAS J,HERRERO J. Correction of propagation errors in wide area multilateration systems[C]∥Proc.of the 6th IEEE European Radar Conference,2009:81-84.

[7] ABBUD J,MIGUEL G,BESADA J. Correction of systematic errors in wide area multilateraltion[C]∥Proc.of the Tyrrhenian International Workshop on Digital Communications-Enhanced Surveillance of Aircraft and Vehicles,2011:173-178.

[8] MANDLIK M,NEMEC Z. An accuracy synchronization method for passive radar system[C]∥Proc.of the 24th International Conference Radioelektronika,2014:1-4.

[9] JIANG C S,LIU C Z,WANG X G. GPS synchronized wide area multilateration system[C]∥Proc.of the International Confe-rence on Communications,Circuits and Systems,2009:457-459.

[10] LI Z,DESISLAVA D,TORSTEN B,et al. Highly accurate evaluation of GPS synchroni-zation for TDOA localization[C]∥Proc.of the International Federation for Information Processing Wireless Days Conference,2013:1-3.

[11] YOON J,KIM J W,LEE W Y,et al. A TDOA-based localization using precise time-synchronization[C]∥Proc.of the 14th IEEE International Conference on Advanced Communication Technology,2012:166-1271.

[12] HAN J,JEONG D. Practical considerations in the design and implementation of time synchronization systems using IEEE 1588[J].IEEE Communications Magazine,2009,47(11):164-170.

[13] 孙海文, 欧阳中辉, 杜亚杰. 载波相位DGPS标校系统时间同步设计与仿真[J]. 海军航空工程学院学报, 2015, 30(4): 336-340.

SUN H W,OUYANG Z H,DU Y J. Design and simulation of time synchronization on alignment calibration system of carrier phase DGPS[J]. Journal of Naval Aeronautical and Astronautical University,2015,30(4):336-340.

[14] RTCA DO-260B.Minimum operational performance standards for 1090MHz extended squitter ADS-B and TIS-B[S]. Washington,DC:RTCA,2009.

[15] ICAO A.10,Aeronautical telecommunica-tions,volume IV:surveillance and collision avoidance systems[S]. 4th ed. Quebec:Inter-national Civil Aviation Organization,2007.

[16] 张涛. 基于SSR应答信号的广域多站定位关键技术研究[D]. 烟台:海军航空工程学院,2016.

ZHANG T. Research on key technologies of wide area multilateration with SSR replies[D]. Yantai:Naval Aeronautical and Astronautical University,2016.

[17] JONES S. ADS-B surveillance separation error sensitivity ana-lysis[R]. Massachusetts:The MITRE Corporation,2009.

[18] BESADA J,GARCIA J,MIGUEL G,et al. ADS bias cancellation based on data fusion with radar measurements[C]∥Proc.of the 3rd IEEE International Conference on Information Fusion,2000,2(2):23-30.

[19] 栾声扬,邱天爽,宋爱民,等. 基于辅助源和相关熵的ADS-B信息时延估计新算法[J]. 通信学报,2015,36(7):102-108.

LUAN S Y,QIU T S,SONG A M,et al. Novel time delay estimation algorithm for ADS-B based on an auxiliary source and correntropy[J]. Journal on Communications,2015,36(7):102-108.

[20] 程擎. ADS-B延迟时间计算方法的可行性分析[J].计算机应用,2012,32(9):2664-2666.

CHENG Q. Feasibility analysis on method of calculating ADS-B latency[J].Journal of Computer Applications,2012,32(9):2664-2666.

[21] 苏志刚,白冰,郝敬堂.ADS-B时间延迟对ADS-B/WAM数据关联的影响研究[J].计算机测量与控制,2016,24(8):229-232.

SU Z G,BAI B,HAO J T. Research on effect of ADS-B latency on ADS-B/WAM data association[J]. Computer Measurement & Control,2016,24(8):229-232.

[22] 郭福成,樊昀,周一宇,等.空间电子侦察定位原理[M].北京:国防工业出版社,2012.

GUO F C,FAN Y,ZHOU Y Y,et al. Localization principles in space electronic reconnaissance[M]. Beijing:National Defence Industry Press,2012.

[23] ARIAS E,PANFILO G,PETIT G. Status of UTC/TAI[C]∥Proc.of the Union Radio-Scientifique Internationale General Assembly and Scientific Symposium Conference,2011:1-4.

[24] 王洪,金尔文,刘昌忠,等.多点定位TOA精确估计及同步误差校正算法[J].系统工程与电子技术,2013,35(4):835-839.

WANG H,JIN E W,LIU C Z,et al. Accurate estimation of TOA and calibration of synchronization error for multilateration[J]. Systems Engeering and Electronics,2013,35(4):835-839.

[25] 沈笑云,唐鹏,张思远,等.ADS-B统计数据的位置导航不确定类别质量分析[J].航空学报,2015,36(9):3128-3136.

SHEN X Y,TANG P,ZHANG S Y,et al. Quality analysis of navigation uncertain category for position based on ADS-B statistical data[J]. Acta Aeronautica et Astronautica Sinica,2015,36(9):3128-3136.

[26] ALI B. A study of ADS-B data evaluation and related problems[C]∥Proc.of the International Technical Meeting of the Institute of Navigation,2013:444-455.

[27] LEVITT I,WILLIAM J. Modeling ADS-B out system latency[C]∥Proc.of the 31st Digital Avionics Systems Conference,2012:1-24.

[28] HOFFMAN E,IVANESCU D,SHAW C,et al. Effect of ADS-B transmission quality on the ability of aircraft to maintain spacing in a sequence[J]. Air Traffic Control Quarterly,2003,11(3):181-201.

[29] POISEL R A. Electronic warfare target location methods[M]. 2nd ed. Massachusetts:Artech House,2012.

[30] KAY S M. Fundamentals of statistical signal processing:estimation theory[M]. Englewood Cliffs,New Jersey:Prentice Hall,1993.