粘贴钢板加固梁的数值分析方法

苏方毅 任学钰 王 凯

中国建筑第七工程局有限公司 河南 郑州 450004

粘贴钢板法在结构加固中的应用越来越多，但粘贴钢板法的数值计算方法有待简化，在实际工程设计中，我们需要设置一定数量的螺栓来辅助黏结层抵抗荷载引起的剪力，防止在钢板没有屈服时黏结层发生破坏。传统的粘贴钢板设计方法大多基于经验公式，一些已有的观点是用线弹性理论进行分析[1-2]，与实际情况偏差比较大。现有的措施对粘贴钢板加固钢筋混凝土梁单独建立了钢筋混凝土、胶结层和钢板3种力学模型来处理[3]。文献[4]用实体单元分别模拟混凝土、钢板及黏结层，假定它们之间不发生滑移，即耦合在一起。本文3种建模方法不考虑粘贴钢板梁中的黏结层，假设其在使用中不发生破坏，以此简化建模难度，而且在计算费用及工程精度间有一个很好的权衡。

钢板与混凝土组合结构，是通过栓钉、螺栓、环氧树脂胶等连接方式，使它们组合在一起形成整体共同工作。桥梁在运行阶段频繁承受车辆荷载的作用，有时甚至超载，桥梁结构会受到损坏或者局部破坏。粘贴钢板加固法施工简洁且非常有效。粘贴钢板的主要流程为：构件表面处理→钢板现场配套打孔与粘贴表面清理→植入钢板固定螺栓→打磨黏结面钢板的表层→黏结胶的配制→在混凝土底面均匀涂抹黏结胶，粘贴钢板，拧紧螺栓。在设计中，要合理选择螺栓的直径、间距以及螺栓的位置，防止在使用过程中钢板的剥离破坏，在结构达到承载能力之前，钢板与混凝土梁可以整体受力，并且钢板达到屈服应力。

1 试验梁基本信息

对文献[5]中控制梁S0、S23、S33进行数值模拟分析，每个梁的净跨间距为2.1 m，长宽高为240 cm×15 cm×25 cm，梁内钢筋布置按表1执行，加载点间的间隔为0.7 m，按跨中对称部位对称加载（图1）。钢板宽度为15 cm，长度200 cm。控制梁S0是没有加固的混凝土梁，S23梁钢板的厚度2 mm，S33梁钢板的厚度3 mm。

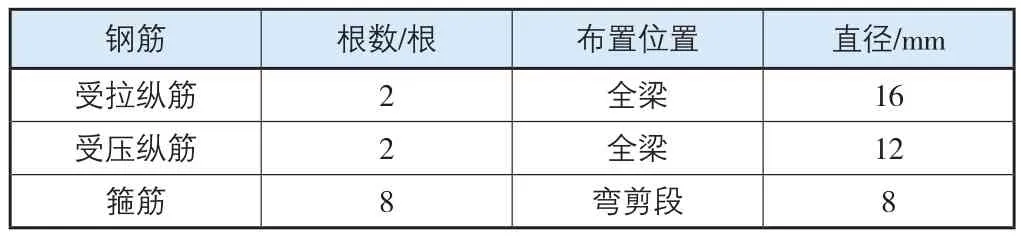
表1 梁内钢筋布置

2 有限元模型

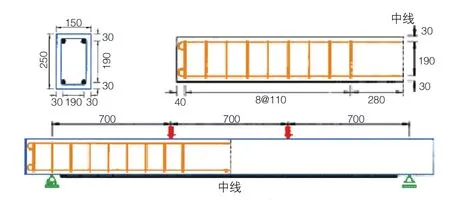
图1 加固梁及加载示意

对梁体采用有限元软件ANSYS进行非线性数值模拟。ANSYS对于混凝土构件有3种主要的有限元模型：分离式、整体式及组合式[6]。分离式主要是用实体SOLID65模拟混现。本实验模型由于要考虑纵筋和箍筋屈服强度的不同，故采用分离式模型来建立。模型主要是在混凝土与钢板间的黏结建立不同处理方式，通过3种不同的数值方法建立。共节点和接触单元模型中，钢板采用SHELL163模拟，厚度通过实常数定义。实体耦合模型中钢板用SOLID45模拟。

2.1 混凝土本构关系

本文所采用的混凝土应力应变关系曲线按照GB 50010—2002《混凝土结构设计规范》规定的公式计算。单轴抗压强度fc=14.0 MPa，单轴抗拉强度ft=1.6 MPa，张开裂缝以及闭合裂缝的剪力传递系数分别取0.5、0.95，泊松比0.2。此处采用多线性随动强化kinh模拟。

2.2 钢材的本构关系

按照理想弹塑性考虑钢筋及钢板材料，受拉纵向钢筋弹性模量200 GPa，屈服强度365 MPa，泊松比取值0.3；主压纵向钢筋弹性模量200 GPa，屈服强度345 MPa，泊松比取值0.3；箍筋弹性模量为200 GPa，屈服强度为420 MPa，泊松比取值0.3；钢板弹性模量209 GPa，屈服强度292 MPa，泊松比取值0.3。为帮助收敛，采用强化阶段的弹塑性模型，在这选用双线性等向强化模型BISO。

3 模型建立的基本过程

3.1 控制梁

控制梁采用分离式模型建立（图2），为节省运算空间，考虑结构对称性，采用1/4模型。加载点为防止局部不收敛，将集中荷载转换为均布荷载，近似代替钢垫板，支座处施加线性约束。为帮助收敛，关闭混凝土压碎，采用位移收敛准则，收敛误差5%，可满足一般工程要求。

3.2 共节点建模

共节点建模（图3）的主要思想是钢板节点与混凝土节点自由度的耦合。主要步骤如下：

1）选择钢板面上的节点并定义钢板节点为元件。

2）GET函数得到钢板节点个数。

3）DIM函数定义钢板节点号组，并存放钢板节点号。定义混凝土节点号组，存放钢板最近的节点号。

4）GET函数得到钢板节点的最小编号，存入钢板节点号组。DO循环依次得到下一钢板节点号，并存入数组，直到得到全部的钢板节点号。

图2 控制梁离散模型

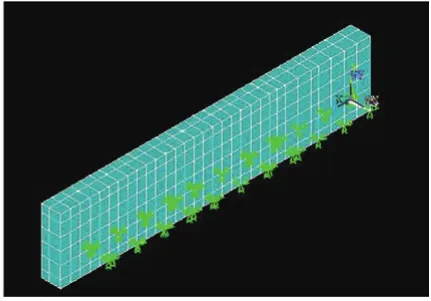
图3 共节点离散模型

5）循环查找钢板距离最近的混凝土节点，将相应的混凝土节点存入数组。

6）循环定义节点耦合集，自由度全部耦合，即Ux，Uy，Uz。为了节省运算成本，采用1/4模型，对混凝土的对称表面通过da,all,symm命令施加对称约束。选定钢板的对称线，通过dl,all,symm对钢板施加对称约束。

3.3 接触单元建模

接触模型（图4）采用CONTA175与TARGE170单元，设置TARGE170的KEYOPT(5)=2，CONTA175的KEYOPT(2)=2，KEYOPT(12)=5。选择钢板的上边面，通过ESURF命令将CONTA175赋予它。选择混凝土的下表面，通过ESURF命令将TARGE170附加到表面。最后通过SHSD将两者装配[7]。采用与共节点模型同样的方法对模型施加对称约束。

3.4 实体耦合建模

钢板采用SOLID45单元，钢板和混凝土划分完网格后，通过vglue,all及nummrg,all命令将钢板与混凝土耦合（图5）[8]。SOLID65单元没有考虑混凝土开裂，即TBDATE参数C3=－1，这样计算结果容易收敛。对钢板以及混凝土表面通过da,all,symm施加对称约束。

图4 接触单元离散模型

图5 实体耦合离散模型

4 模型破坏的理想状态

对于粘贴钢板加固的梁，可能发生多种破坏形式。在设计时，如果能够合理地布置钢板与混凝土之间的连接，钢板与梁能够形成整体共同工作，防止钢板的剥离破坏，这是设计模型最终的破坏形式。钢板能够达到屈服强度，受拉钢筋根据平截面假定，达不到屈服强度，但对于弯曲破坏的混凝土梁，纵筋强度已经非常接近屈服强度，对材料能够很好地利用，没有造成过多的材料浪费。

5 实测结果与数值结果比较

S23、S33梁的试验极限荷载分别为136、137 kN，破坏形式均为板屈服和斜拉破坏，表2给出了3种有限元模拟结果，均可以很好吻合，误差在工程范围10%内，满足工程要求。在钢板不发生剥离的情况下，随着钢板厚度的增加，混凝土梁的承载能力也随之升高。因此，这3种粘贴钢板加固数值方法结果与试验结果均能够很好地吻合，满足工程精度要求。

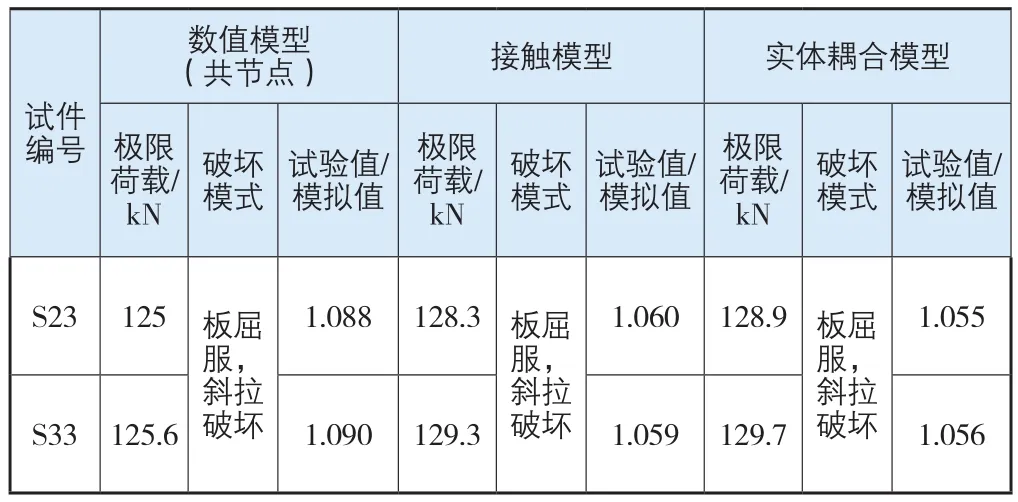
表2 3种有限元模拟结果

本模型只是对于没有发生钢板剥离的粘贴钢板加固梁适用，因为控制梁S0没有进行钢板加固，表现为经典的弯曲破坏形态。梁S23及梁S33都粘贴了一定厚度的钢板，抗弯承载能力有所增大，均表现为剪切破坏形式，梁剪切区域的斜向裂缝延伸并贯穿至梁的上截面，梁纯弯区竖向裂缝发展相比控制梁趋势减弱[9]。图6～图8为控制梁S0及共节点、接触数值模拟S23梁的破坏形态及裂缝的开展情况。

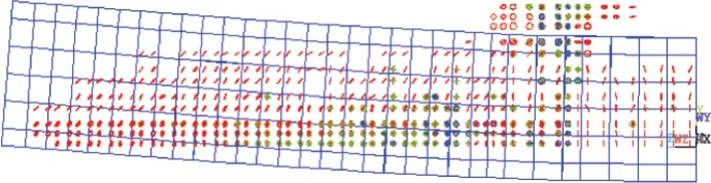
图6 控制梁弯曲破环

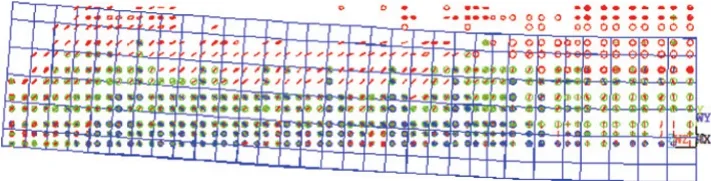
图7 共节点模型剪切破坏

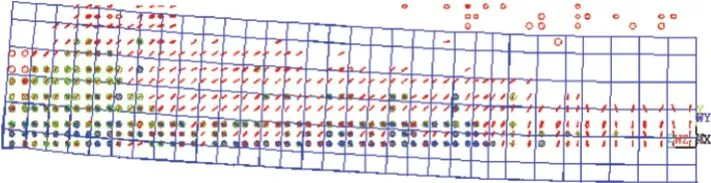
图8 接触模型剪切破坏

图9、图10给出试验梁与3种数值方法模型得到的荷载位移曲线。

表3给出了S23梁试验模型钢筋的极限应变与S23、S33数值模拟极限应变的对比情况。在达到承载能力时，钢板均能够达到屈服应变，纵向受拉钢筋没有达到屈服强度，受压钢筋都达到屈服强度，而且随着钢板厚度的增加，纵向受拉钢筋的极限应变反而降低。对于实际工程中已经修建的桥梁结构，加固钢板的厚度应该有一个界限值，超过界限值时梁的承载能力不再提升。

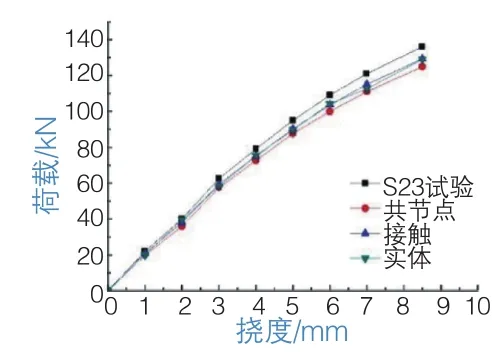
图9 S23及数值模型跨中荷载-挠度曲线

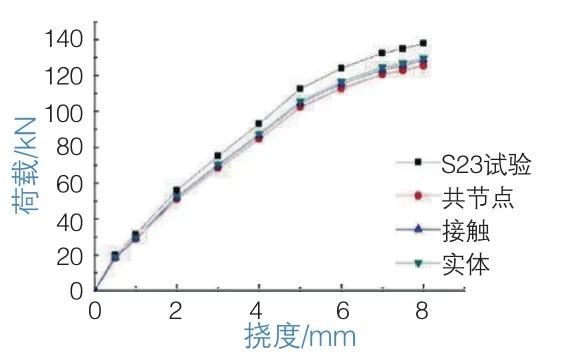
图10 S33及数值模型跨中荷载-挠度曲线

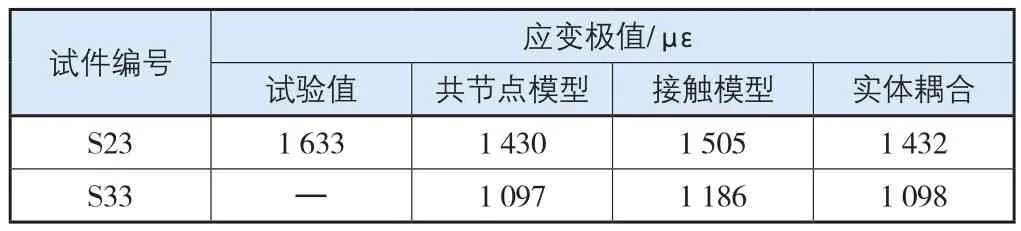
表3 钢筋应变极值

6 结语

本文提出的3种模拟粘贴钢板加固钢筋混凝土梁有限元方法，对于没有发生钢板剥离的混凝土梁，能够准确地模拟粘贴钢板加固梁的破环形态以及承载能力。最主要的是，实体耦合方法适用于一些复杂结构，建模方法简单、思路清晰。尤其对于T梁以及空心板梁这类早期修建桥梁结构，3种方法的计算结果能够为设计提供准确的理论依据，满足工程精度要求。