高速动车组角焊缝应力集中的识别方法
兆文忠,李季涛 ,李晓峰,李向伟,董平沙
(1.大连交通大学 交通运输工程学院,辽宁 大连 116028;2.中车齐齐哈尔交通装备有限公司 技术中心,黑龙江 齐齐哈尔 161002;3.密歇根大学 焊接结构研究中心,美国 安娜堡 48109)
由于焊接结构具有许多独特的优点,弧焊、点焊焊接结构在包括高速动车组在内的轨道车辆产品中扮演着极为重要的角色。然而,在焊接结构传力焊缝上存在着程度不同的应力集中也使其抗疲劳能力明显低于构成母材[1],国内外大量的研究数据[2-5]也证实了这一观点。由于应力集中是影响焊接结构疲劳寿命的最重要因素,因此有效地识别与消除这些因应力集中而导致的疲劳隐患一直是焊接结构设计阶段的一个重点。
在很长的一个时期里,设计人员一直借助于设计手册、设计标准等文件进行抗疲劳设计,这源于他们对英国焊接研究所Gurney T R博士提出的“实际结构和工程构件的疲劳强度是不能用理论的方法求出来的”[6]观点的认同。这些设计手册或设计标准的最大价值在于它们为焊接接头设计提供了一批疲劳试验数据,即基于名义应力的应力—寿命(S—N)曲线数据[7-9]。然而,当一个焊接结构几何形状比较复杂且承受的疲劳载荷也比较复杂时,设计人员将很难从这些设计手册或设计标准中找到合适的疲劳试验数据或S—N曲线数据。
本文基于结构应力法,从焊缝焊趾上非线性应力的分解开始,提出对角焊缝上的应力集中的有效识别方法,给出识别流程,并进行实例计算。
1 基于结构应力法的识别方法
某高速动车组转向架焊接构架上的部分焊接接头三维几何如图1所示。由图1可见:焊接构架的几何形状比较复杂,且承受的疲劳载荷也比较复杂,因此基于名义应力法评估其疲劳寿命时,设计人员很难找到与这几个角焊缝对应的疲劳试验数据。
依据董平沙教授[10]提出的结构应力法,对高速动车组角焊缝应力集中的识别分析时认为:① 在研究角焊缝裂纹扩展时,需要得到焊趾处的应力沿着焊趾所在板厚度方向的分布特征,而不需要得到焊趾所在板表面上某一点的应力;② 根据结构力学理论,将角焊缝截面上的应力分为膜应力和弯曲应力2个部分,前者描述截面上应力状态中均匀分布的部分,后者描述应力状态中应力梯度为线性的部分;③ 虽然角焊缝焊趾处的应力不能通过计算直接获得,但是可以将该处高度非线性的应力分解为两部分:一部分是与外载荷平衡的应力,即满足平衡条件的结构应力,其本质就是外力在角焊缝焊趾处引起的应力集中;另一部分是自平衡的缺口应力,即因焊趾存在缺口而引起的缺口应力[11]。
焊趾所在截面上非线性应力的分解如图2所示。图中:d为板厚度;σx(y)为在焊缝截面上沿厚度方向的应力分布;τ为剪应力;σm和σb分别为沿着板厚度分布的膜应力和弯曲应力。
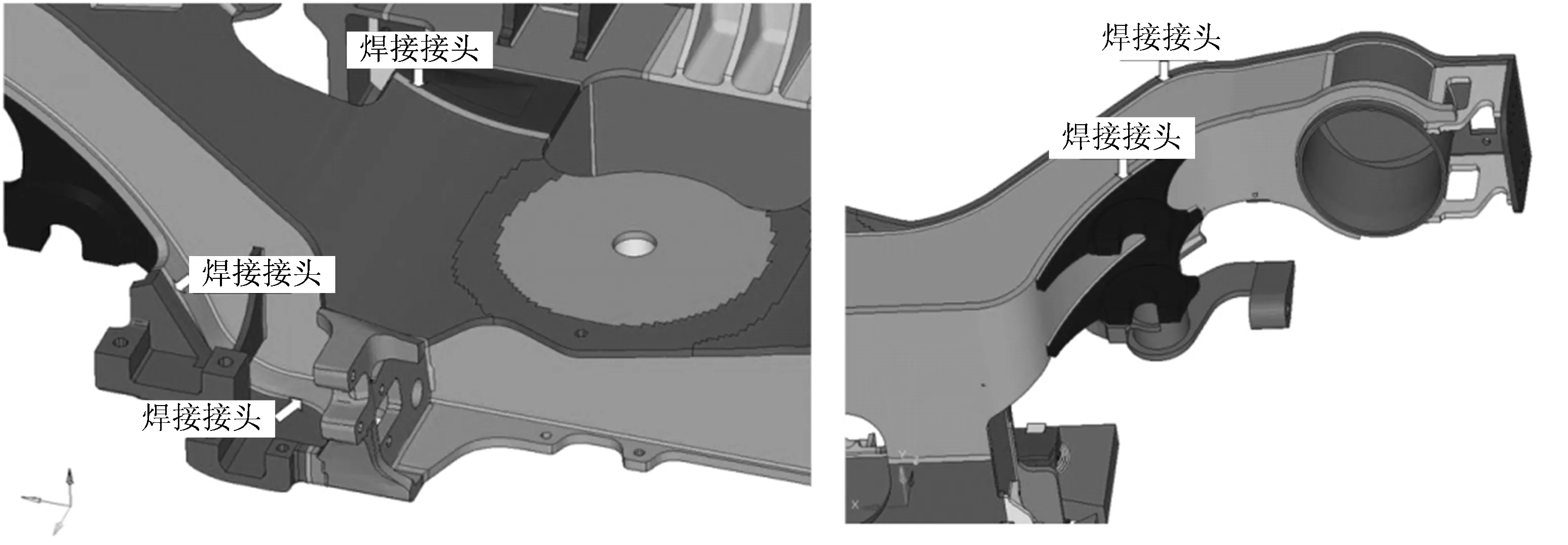
图1 某高速动车组转向架焊接构架上的焊接接头

图2 焊趾所在截面上非线性应力分解示意
虽然在理论上结构应力可以用结构力学公式计算得到,但是在工程上是从有限元求解的后处理文件中提取焊趾上的节点力后再经过一系列变换,并用结构力学公式求解计算得到的。
给定焊接接头焊趾所在板厚以后,参考图2给出的坐标系,截面内产生均匀分布的膜应力和弯曲应力分别为
(1)
(2)
式中:Fy和Mx分别为线力和线力矩,是指将焊趾定义为焊线以后单位长度上的力和力矩。
因结构应力σs为膜应力σm和弯曲应力σb之和,则
(3)
由式(3)可以看出,在计算结构应力时首先要计算线力Fy和线力矩Mx。在有限元计算时,单元边上的分布载荷要向节点转化,而在利用节点力求线力和线力矩时,却是这个过程的逆过程,即需要将有限元求得的节点力和力矩转化为线力和线力矩。
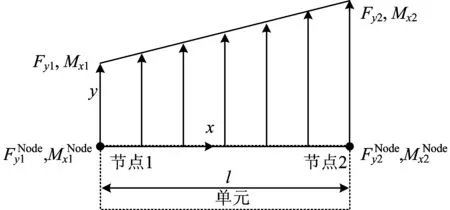
图3 2个节点之间的节点力及线力
根据力的平衡条件,2个节点间的线力用矩阵形式表示为
(4)
同理,2个节点间的线力矩用矩阵形式表示为
(5)
于是节点1与节点2间的结构应力为
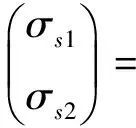
(6)
式中:σs1和σs2分别为节点1和节点2处的结构应力。
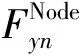
L(Fy1Fy2…Fyn)T
(7)
式中:L为单元长度等效矩阵,只与节点距离相关。
(8)
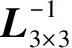
(9)
由此可得线力与节点力的对应关系为
(Fy1Fy2…Fyn)T=
(10)
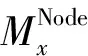
(11)
式(11)即为角焊缝焊趾处结构应力的矩阵形式。结合有限元后处理文件,对上述公式编程即可得到计算结构应力的程序。
2 基于结构应力法的识别流程
图4给出了基于结构应力法的角焊缝应力集中识别流程,其步骤说明如下。① 提出焊接结构初始设计方案,方案中包含角焊缝的具体尺寸;② 创建含焊线(1条焊缝定义2条焊线)的有限元模型,并按疲劳台架试验大纲的要求确定静强度载荷工况,包括液压作动器的具体位置和试验对象在台架上的工装约束;③ 施加边界条件并对每个工况求解;④ 计算结构应力,观察并绘出每个工况下沿焊线分布的结构应力分布,其实该分布就是沿着焊缝的应力集中分布;⑤ 根据应力集中计算结果判断是否满足静强度指标下的安全性要求,如果满足,转向步骤⑥,否则修改设计,转向步骤②;⑥ 根据等效结构应力计算公式,计算考虑了板厚影响以及弯曲比影响的等效结构应力变化范围,根据ASME(2007或2015年)标准,选择计算常数以及标准偏差,计算每个工况下的疲劳损伤;⑦ 基于Miner损伤累积法则,计算总的疲劳损伤;⑧ 如果总的疲劳损伤满足设计要求则结束,否则修改设计,转向步骤②。
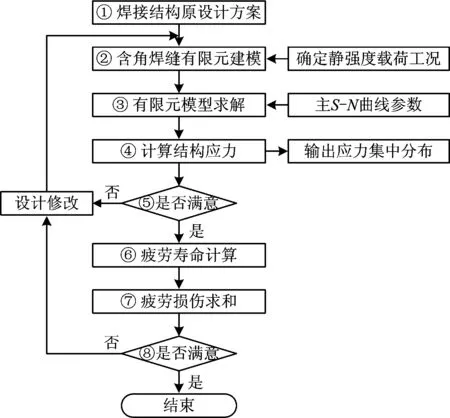
图4 基于结构应力法的角焊缝应力集中识别流程
以当前我国轨道车辆装备制造工厂普遍使用的有限元软件ANSYS为平台,基于图4的计算流程,开发了专用软件WSS(WELDING STRUCTURAL STRESS)。开发工具是C/C++以及ANSYS软件提供的APDL语言,WSS软件由4个基本模块构成:引导模块、前处理模块、计算模块和后处理模块。该专用软件可以在ANSYS求解的结果中自动提取焊线上的节点力。
3 识别实例
下面简要给出1个预测高速动车组焊接构架角焊缝上应力集中与疲劳损伤的实例。某高速动车组转向架焊接构架由2个侧梁和2个横梁组焊而成,对焊结构架上某三维空间焊缝进行有限元建模如图5所示,对模型中1个角焊缝的2个焊趾用2条焊线定义。
按照前述公式,并使用自主开发的专用软件WSS计算出不同载荷工况下结构应力沿着焊缝长度的分布,如图6所示。
由图6可以看出:结构应力的分布清楚地提供了焊缝焊趾处应力集中的峰值及其所在的具体位置,这不仅为疲劳隐患的预判提供了重要的信息,也为分析产生应力集中的原因提供了重要依据。

图5 含角焊缝的某高速动车组焊接构架的有限元模型
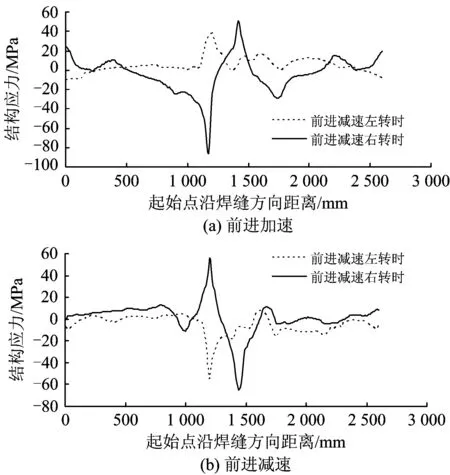
图6 结构应力沿焊线长度的变化曲线
疲劳载荷工况采用UIC515-4[12],疲劳载荷的加载次数取1 000万次,且分3个阶段递增加载,在有限元模型中共定义了132条角焊缝(264条焊线),计算它们的疲劳损伤结果。该结果不仅能给出焊接构架上每条角焊缝上应力集中的具体位置,又能给出具体的峰值及其对应的疲劳寿命,因篇幅所限,部分结果见表1。
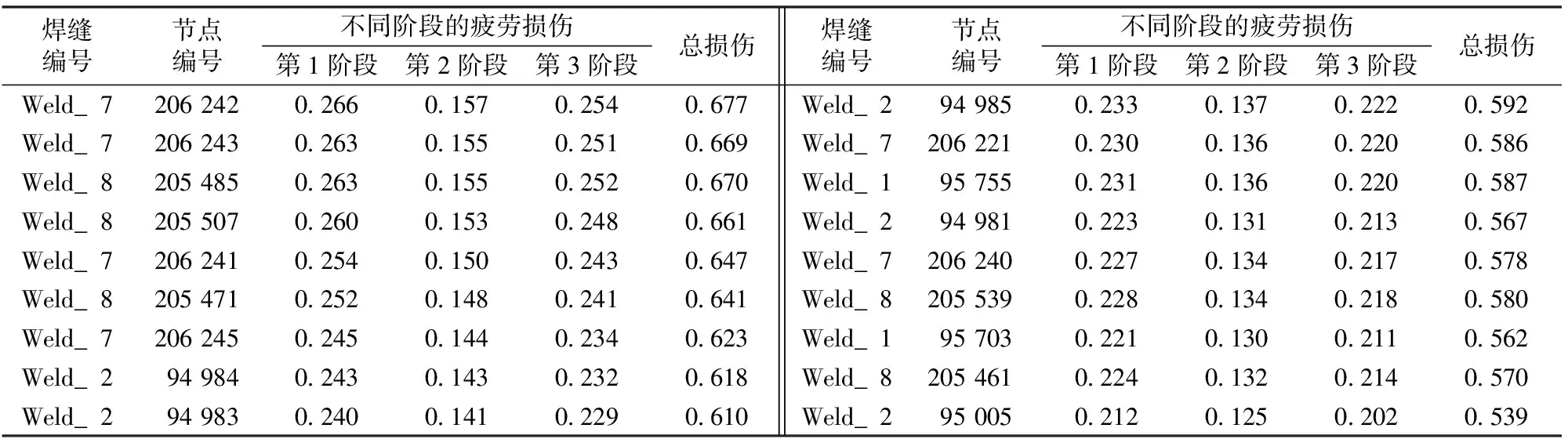
表1 部分角焊缝3个阶段的疲劳损伤结果

续表1 部分角焊缝3个阶段的疲劳损伤结果
4 结 论
(1) 针对高速动车组焊接构架上角焊缝的应力集中识别问题,提出了基于结构应力的识别方法。由于基于理论模型的结构应力具有关于有限元网格不敏感的特点,因此不管焊接构架上角焊缝的分布多么复杂,它都能可靠识别,与传统的名义应力法相比较,结构应力法适用性更广。
(2) 以自主开发的专用软件WSS为工具,并以某高速动车组焊接构架上诸多角焊缝应力集中的识别为应用实例,证明了本文提出的方法不仅能给出焊接构架上每一条角焊缝上应力集中的具体位置,又能给出具体的峰值及其对应的疲劳寿命,因此可用于优化高速动车组焊接构架的抗疲劳设计。
[1]霍立兴. 焊接结构的断裂行为及评定[M]. 北京: 机械工业出版社, 2000.
[2]赵少汴,王忠保. 抗疲劳设计——方法与数据[M]. 北京: 机械工业出版社, 1997.
[3]拉达伊 D. 焊接热效应温度场、残余应力、变形[M]. 熊第京,译. 北京: 机械工业出版社, 1997.
[4]何柏林,于影霞,史建平,等. 应力集中系数对转向架用16MnR钢对接接头疲劳寿命的影响[J]. 中国铁道科学, 2013, 34(6): 89-92.
(HE Bolin, YU Yingxia, SHI Jianping, et al. Effect of Stress Concentration Coefficient on Fatigue Life of 16MnR Steel Butt Joint of Bogie [J]. China Railway Science, 2013, 34(6): 89-92.in Chinese)
[5]周张义,李芾,安琪,等. 钢结构焊缝疲劳强度分析技术的最新进展[J]. 中国铁道科学, 2009, 30(4): 69-75.
(ZHOU Zhangyi, LI Fu, An Qi, et al. Latest Development of Fatigue Strength Analysis Technology for Welds in Steel Structures [J]. China Railway Science, 2009, 30(4): 69-75. in Chinese)
[6]GURNEY T R.焊接结构的疲劳[M]. 周殿群,译.北京: 机械工业出版社, 1988.
[7]British Standard Institute. BS 7608—1993 Fatigue Design and Assessment of Steel Structures[S]. Southampton: BSI, 1993.
[8]IIW Joint Working Group. XIII—1965-03/ XV-1127-03 IIW Document Recommendations for Fatigue Design of Welded Joints and Components[S]. Paris: IIW/IIS, 2003.
[9]Japanese Standards Association. JIS E 4207—2004 Truck Frames for Railway Rolling Stock—General Rules for Design [S]. Japan: JARI/JSA, 2004.
[10]DONG P, HONG J K, OSAGE D A, et al. The Master S-N Curve Method: an Implementation for Fatigue Evaluation of Welded Components in the ASME B&PV Code, Section VIII, Division 2 and API 579-1/ASME FFS-1[M].New York:WRC Bulletin, 2010.
[11]DONG P. A Robust Structural Stress Method for Fatigue Analysis of Offshore/Marine Structures[J]. Journal of Offshore Mechanics & Arctic Engineering, 2005, 127(1): 68-74.
[12]International Union of Railways. UIC 515-4 Test Method of Structure Strength for Passenger Car Bogie [S]. Paris: International Union of Railways, 1993.
[13]刘德昆, 李强, 林浩博, 等. 高速列车转向架构架结构的疲劳可靠性模型[J]. 中国铁道科学, 2017, 38(5):100-106.
(LIU Dekun, LI Qiang, LIN Haobo, et al. Fatigue Reliability Model of Bogie Frame Structure for High-Speed Train[J]. China Railway Science, 2017, 38(5):100-106. in Chinese)
[14]王红, 刘万选, 商跃进. 基于热点应力的国产化Y25型转向架焊接构架疲劳强度分析[J]. 中国铁道科学, 2013, 34(4): 66-70.
(WANG Hong, LIU Wanxuan, SHANG Yuejin. Fatigue Strength Analysis on Welded Frame of Domestic Y25 Bogie Based on Hot Spot Stress[J]. China Railway Science, 2013, 34(4): 66-70. in Chinese)

