随机SIVS传染病模型的持久性和灭绝性

陈易亮，滕志东

(新疆大学数学与系统科学学院，新疆 乌鲁木齐 830046)

0　引言

传染病极大地危害着人类的健康和生活.为了更好地预防和控制传染病，可通过建立相应的数学模型来研究传染病的传播和发展规律.许多学者对确定性传染病模型进行研究，并得到了一些很好的结果.但在现实生活中，传染病在传播过程中不可避免地受到一些随机因素的影响，所以近几年对随机传染病模型的研究得到了广泛重视.[1]由于引入扰动的方法不同，得到的随机传染病模型也不尽相同.引入扰动的方法主要有两种：一种是对确定性模型中的参数进行扰动；另一种是对确定性模型围绕其地方病平衡点进行随机扰动.[2-3]

因为发生率包含了易感者和感染者个体的行为变化和拥挤程度，其对保证传染病模型的准确描述起着关键作用.在许多经典的传染病模型中，双线性发生率和标准发生率被经常使用，如Wang等[4]研究了具有双线性发生率的SIR传染病模型.此外，一些学者对具有非线性发生率的随机传染病模型进行了研究，如Liu[5]研究了具有非线性发生率的随机和确定性SIRS 传染病模型的动力学行为.Zhao等[6]研究了具有饱和发生率的随机SIVS传染病模型

(1)

得到如下结果：

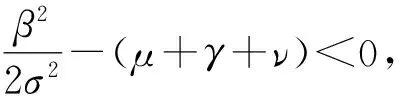
为了更好地描述和预测传染病的动力学行为，在文献[7]的基础上，本文讨论具有非线性发生率的随机SIVS传染病模型

(2)

其中：S(t)和I(t)分别表示种群的易感者和感染者；V(t)表示通过接种获得免疫的人群数量，即接种者；Λ表示人口的输入率；β表示S(t)和I(t)之间的传输率；μ表示自然死亡率；p是对易感者接种的比例系数；q是对新生儿的接种率；δ表示接种个体的丧失免疫率；ν表示因病死亡率；γ表示恢复率；同时假定所有的系数非负.

1　预备知识

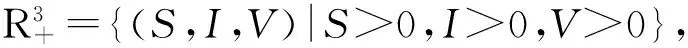
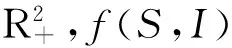
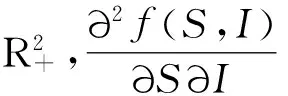
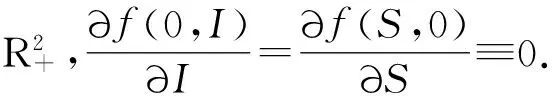
引理1假设(H1)与(H2)成立，D={(S，I)|0≤S≤Λ/μ，0≤I≤Λ/μ}.则

(3)

(4)

即存在常数M1>0，∀(S，I)∈D，

证明(3)式显然成立.对(S，I)∈D，定义函数

由L’Hospital准则，

因此对于(S，I)∈D，H(S，I)和G(S，I)均连续，故(4)式成立.

是系统(2)的正向不变集.

这个引理可用类似文献[7]的方法证明，这里省略.

由引理1，d(S+I+V)≤[Λ-μ(S+I+V)]dta.s.，于是

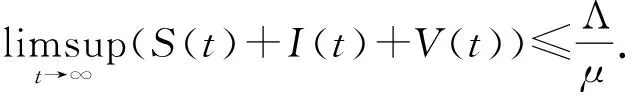
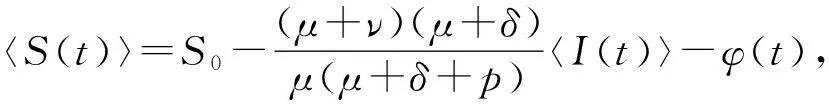
这个引理可用类似文献[6]的方法证明，这里省略.

令

2　疾病的灭绝性

证明对系统(2)的第二个方程应用It公式得

(6)

对(6)式两边从0到t进行积分，再同时除以t有

(7)

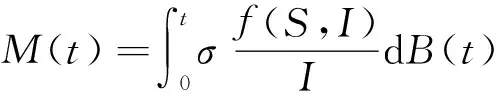
2012年前后，杭州市政府大力探索智慧城市建设，区域医疗信息化建设推进迅速，希望实现医疗机构互联互通，达成“智慧医疗”概念。最终，市民卡成为患者进入杭州医疗服务体系的一个“公共载体”。这些网络基础设施建设，为医院一系列后续流程变革创造了条件。

若条件(A)成立，则有

若条件(B)成立，由假设条件(H1)，(H2)及中值定理，

(8)

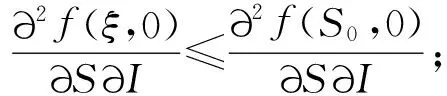
(9)

对充分小的常数ε>0，由(7)式得

(10)

由(7)和(8)式及引理2，进一步有

(11)

(12)

(13)

从而有

(14)

当ε→0时，

(15)

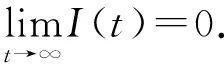
3　疾病的持久性

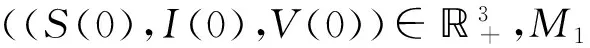
其中

由中值定理，存在(ξ，θ)∈D，η位于S0和S之间，使得

从而

对上式两边从0到t进行积分再除以t，由引理2得

故

因为(ξ，θ)∈Γ，由引理1可知

再根据假设(H1)，

从而

由于

从而

同理可得

因此

进一步地，

并且

此外，

由于

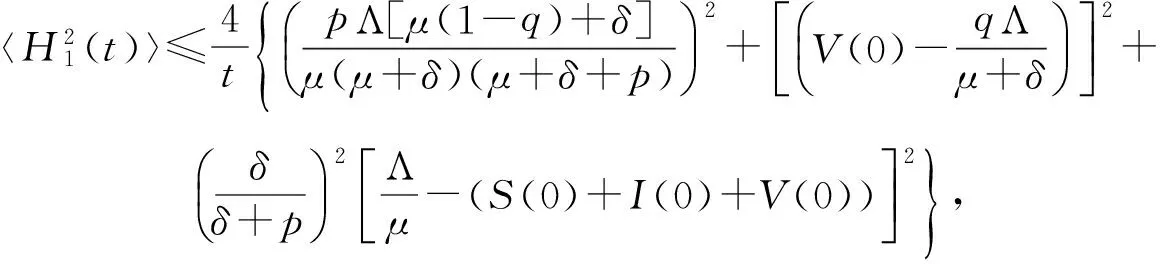
综上，

4　总结

[参考文献]

[1]TORNATORE E，BUCCELLATO S M，VETRO P.Stability of a stochastic SIR system[J].Physica A：Statistical Mechanics & Its Applications，2005，354(1)：111-126.

[2]SANTONJA F J，SHAIKHET L.Probabilistic stability analysis of social obesity epidemic by a delayed stochastic model[J].Nonlinear Analysis Real World Applications，2014，17(1)：114-125.

[3]MENG XIN-ZHU.Stability of a novel stochastic epidemic model with double epidemic hypothesis[J].Applied Mathematics & Computation，2010，217(2)：506-515.

[4]WANG J J，ZHANG J Z，JIN Z.Analysis of an SIR model with bilinear incidence rate [J].Nonlinear Analysis Real World Applications，2010，11(4)：2390-2402.

[5]LIU Q，CHEN Q.Analysis of the deterministic and stochastic SIRS epidemic models with nonlinear incidence[J].Physica A：Statistical Mechanics & Its Applications，2015，428：140-153.

[6]ZHAO D，ZHANG T，YUAN S.The threshold of a stochastic SIVS epidemic model with nonlinear saturated incidence[J].Physica A：Statistical Mechanics & Its Applications，2016，443：372-379.

[7]ZHAO Y，JIANG D，O’REGAN D.The extinction and persistence of the stochastic SIS epidemic model with vaccination[J].Physica A：Statistical Mechanics & Its Applications，2013，392(20)：4916-4927.