基于扩展粒子群优化的支持向量机短时交通流预测

王锦添，蔡延光，黄何列，戚远航

（广东工业大学 自动化学院，广东 广州 510006）

1　引言

随着城市化进程的加快，交通拥堵问题日益严重，对人们的出行带来了极大困扰，但也促进了智能交通系统的快速发展. 智能交通系统对城市交通控制、交通诱导和交通管理有着至关重要的作用，它起到了监测、预测、分流、调度等作用，从而提高了城市道路的利用率. 而影响其作出决策的一个重要参数就是道路的交通流. 能否对城市道路的交通流进行实时、准确的预测，是评价一个智能交通系统好坏的重要因素. 因此，多年来，道路交通流预测都是智能交通领域内的一个研究热点，国内外学者为此提出了多种预测方法. 根据其预测时间的跨度，对交通流预测又可以分为短时交通流预测和长时交通流预测. 在这两种预测中，又以短时交通流预测最为热门.

目前，常用的短时交通流预测算法有卡尔曼滤波算法[1－2]、K邻近算法[3－5]、神经网络模型[6－9]和支持向量机模型[10－11]等，其中，支持向量机以其小样本、精度高等特点得到广泛应用，但支持向量机模型中的参数设置较为困难，常用的方法是采用网格搜索法[12]进行寻优. 该方法首先估计参数的大致取值范围，然后设置步长，通过不断缩小范围而寻找到一组使支持向量机性能最优的参数. 虽然采用网格搜索方法能够找到使支持向量机性能很高的一组参数，也即全局最优解，但如果想在更大的范围内寻找最优的一组参数时就会非常费时. 因此，近年来，有学者采用启发式算法对支持向量机的参数进行寻优，有效避免了网格搜索法需要遍历所有解和费时的缺点，同时也能找到全局最优解. 例如：混沌云粒子群优化算法[13]，基于蝇优化的最小二乘支持向量机[14]，利用PSO算法优化基于联合核函数的最小二乘支持向量机模型等[15]，在以上算法中，虽然对支持向量机模型参数优化做了很多研究，但是还没有将扩展粒子群优化算法（Extended Particle Swarm Optimization， EPSO）和支持向量机结合的短时交通流预测方法. 扩展粒子群优化算法不仅具有标准粒子群优化算法的优点，而且改善了标准粒子群优化算法容易陷入局部最优的问题。因此，本文试图采用扩展粒子群算法优化支持向量机模型参数，使得支持向量机模型在预测交通流的应用上性能有所提高.

2　支持向量机

支持向量机是由Vapnik提出的，用于模式分类和非线性回归，它的主要思想是以一个分类超平面作为其决策面，并使正例与反例之间实现边缘最大化.

已知训练集（Xi，Yi），其中Xi为输入向量，Yi为输出向量，支持向量机通过引入一个非线性函数φ（x），将输入数据映射到另一个高维特征空间中，并在此空间构造一个线性决策函数，这样就使得原来的非线性问题转化为线性问题.

式（1）就是线性决策函数，其中l为训练样本数.

另外，引入一个不敏感损失函数：

使用它来求解出一个f（x），它使得式子最小. 其中，ε称为不敏感损失参数，C称为惩罚参数，w为一个线性权值向量w＝[ω1，ω2，…，ωN]T

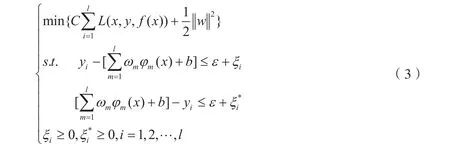
从而转化为一个二次规划问题的求解，因此，可以引入一个核函数K（xi，x），然后利用拉格朗日乘子法并进行对偶化操作，可以得到如下式子：

最后可以归结为：

其中核函数K（xi，x）有多个种类，包括线性核函数、多项式核函数、径向基核函数和两层感知核函数. 由于线性核函数是径向基核函数的一个特例，而两层感知器核函数在特定的参数条件下又与径向基核函数相同，多项式核函数与径向基核函数相比自身参数个数太多，所以本文选取只有一个自身参数σ的径向基函数作为支持向量机核函数，其函数形式如下：

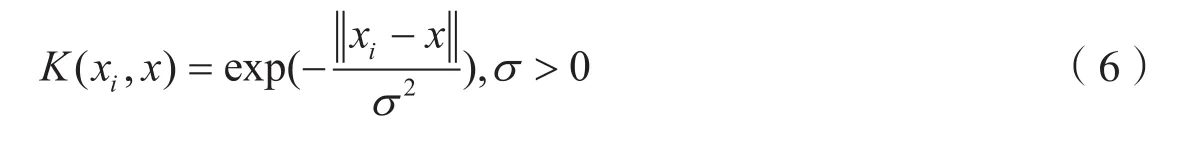
3　基于扩展粒子群优化的支持向量机

3.1　标准粒子群优化算法

支持向量机有着小样本、精度高的特点，非常适合大数据处理预测，但是仍然有3个参数是需要辨识的. 当选择径向基函数作为核函数时，其整个模型所需辨识的参数为最少，只有3个，分别为惩罚参数C、不敏感损失参数ε和核函数自身参数σ. 目前对于支持向量机这个参数在国际上并没有一个公认的好的辨识方法. 传统方法是通过网格搜索法来寻找出使得模型训练效果最优的一组参数，其主要思想是首先根据经验估测各个参数的大致范围，然后用算法不断缩小范围，最终经过多次尝试后才能确定出一组能够满足精度要求的参数值，这种传统方法费时费力，由此产生了利用其他具有寻优特性的算法来代替这种方法.

粒子群优化算法是一种基于群体智能的演化计算技术，它具有收敛速度快、参数少的特点，相比于网格搜索法，是一种效率非常高的并行搜索算法，近年来越来越多的学术研究者用它来进行模型参数的寻优.

粒子群优化算法的主要描述为：在目标搜索空间中，有一个由n个粒子组成的粒子群，每个粒子包含了两个D维的向量，一个是位置向量xi=（xi1，xi2，…，xiD），另一个是速度向量vi＝（vi1，vi2，…，viD）. 粒子群中存在着一个适应度函数f（x），用来衡量粒子在整个解空间中的好坏. 因此，在整个粒子群进行解空间搜索时，会产生两个最优极值，一个是个体最优极值pi＝（pi1，pi2，…，piD），它是每个粒子在更新迭代过程中所出现过的历史最优极值；另一个是群体最优极值它是整个粒子群在更新迭代过程中所出现过的历史最优极值. 在粒子的更新过程中，粒子的位置向量和速度向量就是根据这两个最优极值来进行更新的. 其更新公式如下：

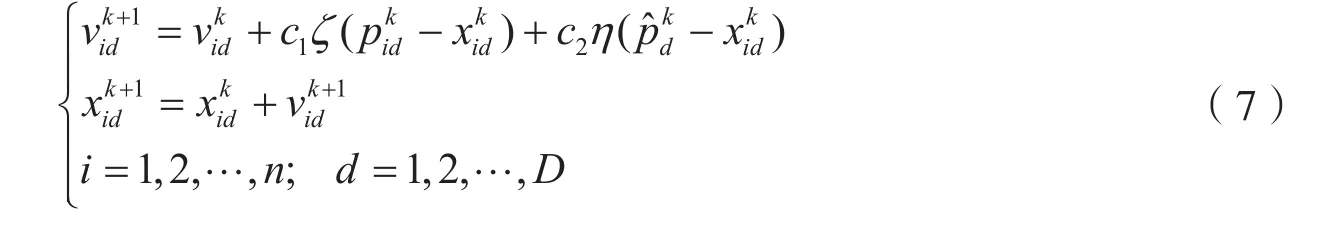
式中：c1、c2被称为学习因子，都是非负常数；ζ、η都是随机数，取值区间为（0，1）.

3.2　扩展粒子群优化算法

虽然相较于网格搜索法而言，粒子群优化算法在寻优速度和参数精度上有了较大的提高，但是仍然避免不了它自身所存在的缺点，容易陷入局部最优值，使得整个算法进程停滞不前，不能往更高精度方向搜索. 因此，国内外学者提出了很多方法来改善粒子群优化算法这个缺点. 例如，在粒子更新迭代过程中加入自适应算子，使得粒子具有一定概率产生变异，从而从局部最优值中跳出来；又或者与混沌算法结合[16]，使得粒子具有混沌特性，不易陷入局部最优值.

扩展粒子群优化算法，在粒子的更新迭代过程加入了更多的粒子迭代寻优过程信息，使得算法收敛得更快，有效解决容易陷入局部最优值的问题. 扩展粒子群优化算法与标准粒子群优化算法相比，只是在粒子的更新公式上有所不同，其更新公式如下：

从上述更新公式可以看出，该扩展粒子群优化算法在更新迭代过程中根据粒子前h个个体最优极值和整个粒子群的前q个群体最优极值的信息来更新当前粒子的速度和位置，这样使得粒子有效避免容易陷入局部最优值，同时相比其他改进的粒子群优化算法，比较简单，容易操作. 因此整个扩展粒子群优化算法的步骤如下.

步骤1：确定寻优参数个数D，以此构建一个D维的粒子；

步骤2：随机初始化整个粒子群，包括学习因子c1、c2等；

步骤3：通过适应度函数f（x）计算出各个粒子的适应度值；

步骤4：根据适应度值选取个体最优极值和群体最优极值；

步骤5：若适应度值满足要求或者达到迭代次数，则算法结束；否则转到步骤6；

步骤6：根据式（8）来更新粒子的速度和位置向量，转到步骤3.

3.3　基于扩展粒子群优化的支持向量机建模

在利用基于扩展粒子群优化的支持向量机建模之前，需要对数据进行预处理. 常规的预处理就是只有归一化，而对于交通流数据，由于其特殊性，除了要进行归一化处理外，还需要对样本进行构造处理.

首先，归一化处理采用最常见的最大最小归一化处理，其处理公式为：

式中，a’i是归一化处理后的数据；ai是归一化处理前的数据；amin，amax分别为归一化处理前样本数据集中的最小值和最大值.

对样本数据进行归一化处理后，再对样本进行重新构造. 考虑到算法的复杂度以及运算量，本文参考国内外学者的文献以及实际情况，采用嵌入维数为5来重新构造样本数据. 其构造原理如下：假设有某时间段内交通流量数据序列a（n），从中可以构造出一个训练样本（X，y）＝[（xi，yi）|i＝1，2，…，n]，其中xi＝（ai，ai＋1，ai＋2，ai＋3，ai＋4）为第 i个样本点的输入向量，yi＝ai＋5为对应的第i个输出值 . 形式如下：

在进行完预处理后，采用支持向量机进行建模. 其中需要辨识的模型包括：惩罚参数C、不敏感损失参数ε和核函数自身参数σ. 然后利用扩展粒子群算法对这3个参数进行寻优辨识，其详细寻优步骤如下.

步骤1：由需要寻优的参数，惩罚参数C、不敏感损失参数ε和核函数自身参数σ组成一个三维的粒子；

步骤2：随机初始化粒子群，包括学习因子c1、c2等，种群大小为20，迭代次数为2000；

步骤3：通过适应度函数f（x）计算出各个粒子的适应度值，其中本文采用平均相对误差作为适应度函数：

式中n为训练样本的样本数目；yi为第i个样本的真实值；y’i为第i个样本的预测值.

步骤4：根据适应度值选取个体最优极值和群体最优极值；

步骤5：若适应度值满足要求或者达到迭代次数，则算法结束；否则转到步骤6；

步骤6：根据式（8）来更新粒子的速度和位置向量，转到步骤3.

获取到最优的一组参数后，将这组参数应用到预测模型中，并用新的数据进行泛化测试. 整个建模流程如图1所示.

图1　算法建模过程

4　实验验证与分析

4.1　数据来源及仿真环境

本文选取由广州市交通流监测系统提供的某路口2016年4月1日至6月30日的数据作为样本数据集. 该数据集每天的数据从00：00开始采集，采集时间间隔为15 min，至23：45结束，每天共采集96个交通流数据. 选取4月1日至6月20日的样本数据作为训练集，选取6月21日至30日的样本数据作为测试集.

对于本文的样本数据集，采用嵌入维数为5来重构训练样本，即输入数据的维数为5，输出数据的维数为1，所得输入输出样本训练集的形式如式（10）所示.

然后寻找使模型训练效果最好的一组参数. 本文利用扩展粒子群优化算法对支持向量机中3个参数惩罚参数C、不敏感损失参数ε和核函数自身参数σ进行寻优. 对扩展粒子群优化算法中的参数值以及参数取值范围进行设置：粒子群大小为20；解空间为3维，分别对应惩罚参数C、不敏感损失参数ε和核函数自身参数σ的取值，取值范围分别为：C为[0.01，500]，σ为[0.1，10]，ε为[0.01，10]；最大迭代次数为2 000；加速因子c1=c2=2.

本文进行的所有实验均在同一实验环境中进行，其中CPU为Intel（R） Core（TM） i5－4210M@2.60 GHz，内存为12 GB，操作系统为64位Windows 7，仿真软件为MATLAB R2014a，在程序中调用了libsvm.

4.2　参数优化

为了验证本文优化方法的计算速度，分别采用扩展粒子群算法、标准粒子群算法和传统网格搜索法对支持向量机模型参数进行优化，3种参数优化方法结果及时间如表1所示.

从表1可以看出，扩展粒子群算法优化速度最快，标准粒子群算法优化速度比扩展粒子群算法稍慢，网格搜索法的优化速度最慢，从而验证了扩展粒子群算法优化支持向量机的速度优势.

表1　参数优化结果及时间

4.3　效果分析

支持向量机经过扩展粒子群优化得到一组最优参数为C＝143、σ＝0.1、ε＝0.01. 将这组参数代入到支持向量机模型中重新训练，最终得到经过扩展粒子群优化的支持向量机预测模型. 利用样本测试集测试经过扩展粒子群优化的支持向量机预测模型的泛化预测能力，图2所示为测试集中的6月21日各时段的预测结果. 从图2可以看出，基于扩展粒子群优化支持向量机所取得的预测结果与实际交通流数据拟合程度较高，其预测效果良好；各个数据采集点的预测数据与实际数据之间的相对误差较小，基本都在20以下.

为了定量分析本文预测模型的预测性能，将本文预测模型分别与传统网格搜索法和标准粒子群算法优化的支持向量机模型比较，采用一天的平均相对误差（Mean Relative Error， MRE）作为预测效果的评判标准，其公式如下：

图2　本文预测模型一天的预测结果

从表2可以看出，基于扩展粒子群优化支持向量机所取得的预测效果普遍好于其他两种优化算法，而且经过计算，3种优化模型10 d的平均MRE分别为：扩展粒子群法9.45%，标准粒子群法11.83%，网格搜索法11.29%.

综合表1和表2可以看出，基于标准粒子群优化支持向量机所取得的预测效果与常用的基于网格搜索法优化支持向量机相比，虽然其预测效果略有不足，却胜在省时省力，优化时间少了1 189 s. 而相比其他两种优化算法，用扩展粒子群优化支持向量机的优化时间最少，而且其取得的预测效果相比常用的网格搜索法提高了16.30%，相比标准粒子群优化算法提高了20.11%. 所以，用扩展粒子群优化支持向量机不仅优化时间快，而且预测结果相比其他两种优化算法在精度上有明显提高，验证了本文方法在交通流预测中的可行性和有效性.

表2　3种优化模型每天的平均相对误差结果

5　结束语

支持向量机具有小样本、精度高等特点，非常适合于交通流预测. 利用扩展粒子群优化算法对预测模型中的3个参数惩罚参数C、不敏感损失参数ε和核函数自身参数σ进行寻优，不仅避免了传统的网格搜索法中耗时费力的缺点，而且相较于标准粒子群优化算法有效避免了其容易陷入局部最优的问题，并且搜索精度进一步提高. 实验分析表明，基于扩展粒子群优化的支持向量机预测模型在交通流预测中要好于网格搜索法和标准粒子群优化的支持向量机预测模型，能够满足短时交通流预测的需要.

参考文献：

[1]DENG M J， QU S R. Fuzzy state transition and kalman filter applied in short－term traffic flow forecasting[J]. Computational Intelligence and Neuroscience， 2015， 2015：1－7.

[2]朱征宇，刘琳，崔明. 一种结合SVM与卡尔曼滤波的短时交通流预测模型[J]. 计算机科学，2013，40（10）：248－251.

[3]YU B， SONG X， GUAN F， et al. K－nearest neighbor model for multiple－time－step prediction of short－term traffic condition[J]. Journal of Transportation Engineering， 2016， 142（6）：1－10.

[4]CAI P， WANG Y， LU G， et al. A spatiotemporal correlative k－nearest neighbor model for short－term trafficmultistep forecasting[J]. Transportation Research Part C－Emerging Technologies， 2016， 62：21－34.

[5]侯晓宇，吴萌，李要娜. 基于双层K近邻算法的短时交通流预测[J].交通标准化，2014，42（7）：1－9.

[6]YANG H J， HU X. Wavelet neural network with improved genetic algorithm for traffic flow time series prediction[J]. Optik，2016， 127（19）：8103－8110.

[7]KAZEMI R， ABDOLLAHZADE M. An adaptive framework to enhance microscopic traffic modelling： an online neuro－fuzzy approach[J]. Proceedings of the Institution of Mechanical Engineers Part D－Journal of Automobile Engineering， 2016， 230（13）： 1767－1779.

[8]LI H. Research on prediction of traffic flow based on dynamic fuzzy neural networks[J]. Neural Computing & Applications，2016， 27（7）：1969－1980.

[9]张琛， 徐国丽. 基于云遗传的RBF神经网络的交通流量预测[J]. 计算机工程与应用， 2014， 50（16）：216－220.

[10]王珂， 田瑞， 王菲菲. 基于灰色遗传支持向量机的短时交通流预测[J]. 武汉理工大学学报（交通科学与工程版），2014， 38（5）：1006－1010.

[11]刘静. 基于AFSA－LSSVM的短时交通流量预测[J]. 计算机工程与应用， 2013， 49（17）：226－229.

[12]唐世星， 柯凤琴. 基于改进的SVM的短时交通流预测[J]. 煤炭技术， 2012， 31（5）： 208－209.

[13]LI M W， HONG W C， KANG H G. Urban traffic flow forecasting using Gauss－SVR with cat mapping， cloud model and PSO hybrid algorithm[J]. Neurocomputing， 2013， 99： 230－240.

[14]HU W， YAN L， LIU K， et al. A Short－term Traffic Flow Forecasting Method Based on the Hybrid PSO－SVR[J]. Neural Processing Letters， 2016， 43（1）：155－172.

[15]CONG Y， WANG J， LI X. Traffic Flow Forecasting by a Least Squares Support Vector Machine with a Fruit Fly Optimization Algorithm[J]. Green Intelligent Transportation System and Safety，2016，137：59－68.

[16]SHANG Q， LIN C， YANG Z， et al. Short－term traffic flow prediction model using particle swarm optimization－based combined kernel function－least squares support vector machine combined with chaos theory[J]. Advances in Mechanical Engineering，2016，8（8）：1－12.