具两相同热储备部件可修系统的渐近稳定性分析

乔　兴

（大庆师范学院　教师教育学院，黑龙江　大庆　163712）

1　引言

文献[1][2]中用补充变量方法建立了此可修系统的数学模型，并用Laplace变换分析了系统的可用度，得到了一系列有意义的结果.但上述结论的取得依赖于如下两个条件：条件（1）该系统存在唯一非负时间依赖弱解.条件（2）该时间依赖解是渐近稳定的[3].当故障后的修复时间服从指数分布时，上面两个条件成立.当故障后的修复时间服从任意分布时，上面提到的两个条件是否成立仍有待于研究.作者的意图是提出两个条件成立的结论，为此类可修系统的可靠性研究提供严格的理论基础.在文献[4]中柳等人给出了系统唯一非负解是0本征值所对应的本征向量的结论，即验证了上面条件（1）成立.在本文中我们通过研究算子的谱点分布，检验了算子的谱点除虚轴上0点外均位于左半复平面，得到了该系统的渐近稳定性分析，即证明了上面提到的条件（2）.

2　模型描述

文献[5]中作者已经给出了系统的解唯一存在的结论.在本文中我们将给出该可修复系统的渐近稳定性分析过程.有了上面的准备，可得描述此模型的积分—微分方程组[6]：

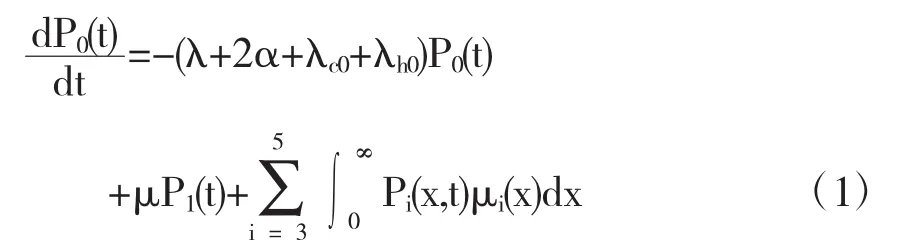
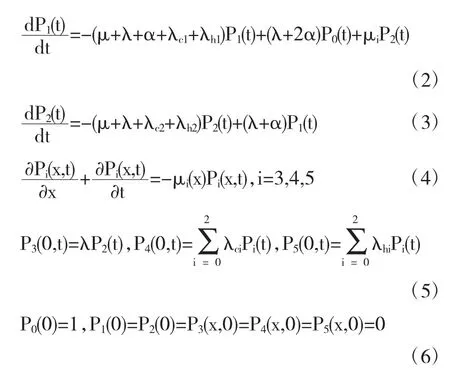
其中i=0时刻代表1个部件工作、2个部件热储备的状态.i=1时刻代表1个部件工作、1个部件发生故障、1个部件热储备状态.i=2时刻代表1个部件工作、2个部件发生故障的状态.i=3时刻代表3个部件均发生故障的状态.i=4时刻代表该系统处于常规故障的状态.i=5时刻代表该系统处于人为故障的状态.λ代表运行系统由自身原因引起的损坏率.λci代表在状态i时刻系统的常规故障率(i=0,1,2).λhi代表在状态i时刻系统的人为故障率(i=0,1,2).α代表热储备部件的损坏率.μ代表运行部件的常数修复率.Pi(t)代表t时刻该系统处于状态i的概率(i=0,1,2).Pi(x,t)代表t时刻该系统处于状态i且已修时间为 x 的概率，(x,t)∈[0,∞)×[0,∞).μi(x)代表时刻系统处于状态i时的修复率，且满足

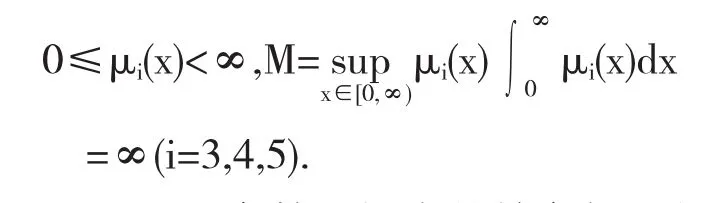
下面用巴拿赫空间中的抽象柯西问题来刻画上面积分——微分方程组，为方便，记：

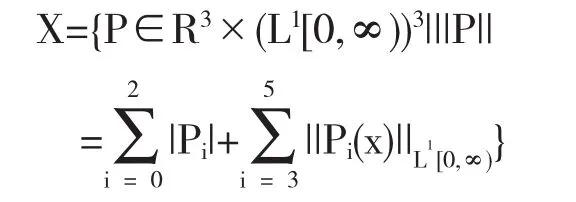
显然(X,||·||)为巴拿赫空间.取算子A的定义域如下：

D(A)= ｛ P∈X|Pi(x)(i=3,4,5)是绝对连续的函数，

则系统方程（1）—（6）可描述为巴拿赫空间中的一个抽象柯西问题（ACP）：

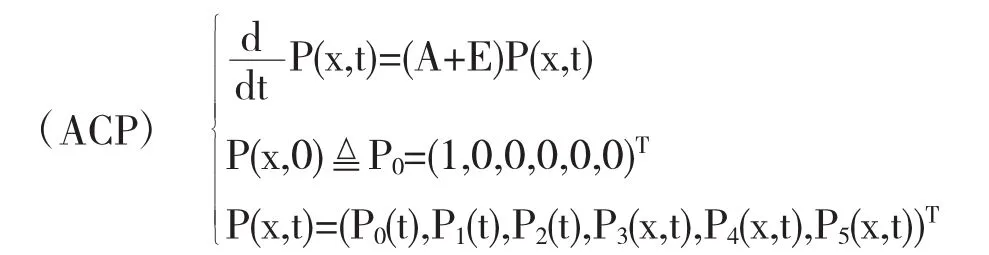
3　解的渐近性

为了在后面的论证过程中方便，我们先给出两个非常有用的引理.

引理1设部件寿命是非负的连续型随机变量x，其分布函数是Gi(x)，密度函数是gi(x)且Gi(0)=0，则有：则当{γ∈C|Reγ＞0 或 γ=ia,a∈R,a≠0}时，有 |g|＜1.

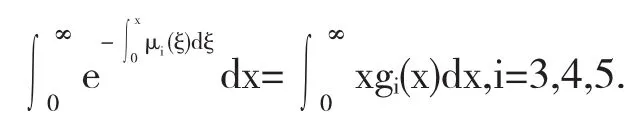
定理10是算子A+E的简单本征值.证明考虑如下方程组得：

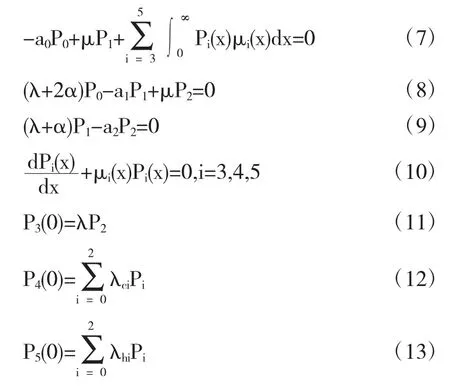
引理2记g=

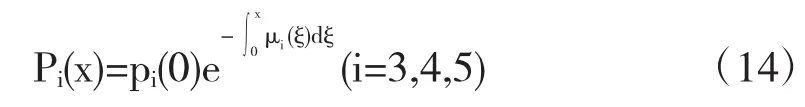
将（14）代入（7）并联立（8）—（9）可得：

(-a0+λc0+λh0)P0+(μ+λc1+λh1)P1+(λ+λc2+λh2)P2=0，

(λ+2α)P0-a1P1+μP2=0，

(λ+α)P1-a2P2=0，

容易验证上述方程的系数行列式的值为0，并且当 P0＞0 时，P1,P2均大于零.同时由 P0＞0 和 a0,a1,a2的表达式知Pi(x),i=3,4,5均是非负的，因此向量P*=(P0,P1,P2,P3(x),P4(x),P5(x))是算子A+E的0本征值对应

定理 2{γ∈C,Reγ＞0 或 γ=ia,a∈R,a≠0}⊆ρ(A+E).

证明对任意给定的 γ∈C，Reγ＞0或 γ=ia，a∈R，a≠0,=(y0,y1,y2,y3(x),y4(x),y5(x))∈X.解方程(γI-A-E)P=y→得

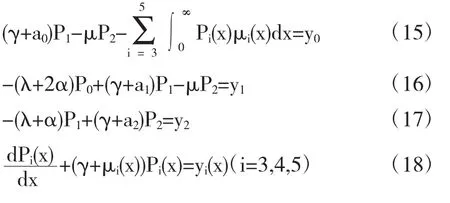
解（18）得

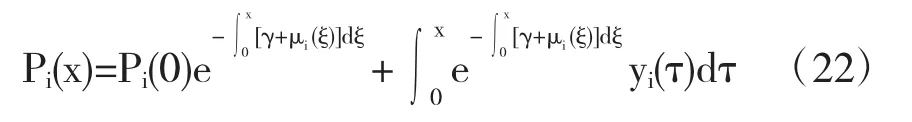
因为 yi(x)∈L1[0,∞)i=3,4,5，结合引理 2有：

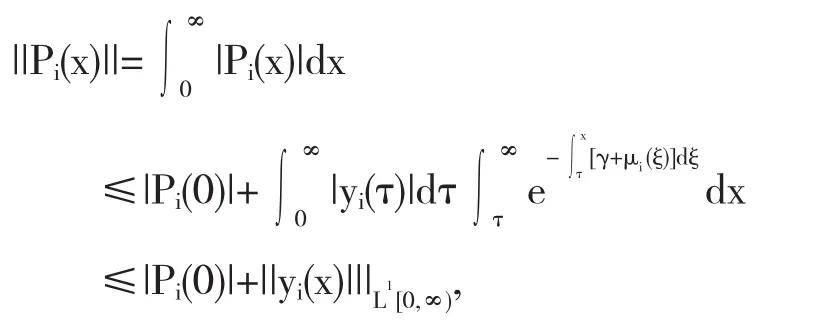
故 Pi(x)∈L1[0,∞),i=3,4,5.将其代入（15）并联立（16）—（17）有：

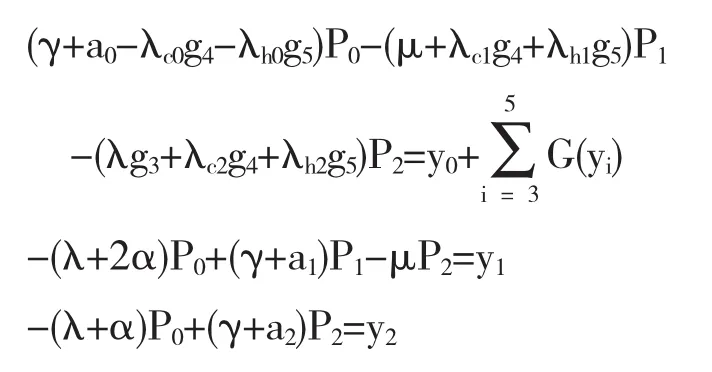
其中：gi=

当 Reγ＞0 或者 γ=ia,a∈R,a≠0 时，有 |gi|＜1，故可得上面方程组的系数矩阵是严格对角占优矩阵.根据文献[7]可知，系数行列不等于零.从而当→=(y0,y1,y2,y3(x),y4(x),y5(x))≠0 有：P=(P0,P1,P2,P3(x),P4(x),P5(x))≠0即上述方程存在唯一解，故R(γ-A-E)=X，又因为(I-A-E)是闭算子，由文献[8]可知(γ-A-E)-1存在且有界，即{γ∈C,Reγ＞0 或 γ=ia,a∈R,a≠0}属于算子A+E的预解集.

上述结论对于其它各科教师当然也是成立的．更一般地说，这也正是医生、律师等具有较强实践性质的专业人员何以需要较长见习期的主要原因，即是工作的复杂性与不确定性，从而就不可能被完全纳入任一固定的理论框架．这也就是指，即使相关人士已较好地掌握了相关的专业知识，仍然不可能通过这些知识的简单应用就能有效地解决所面临的各种问题，而必须主要依靠自身的创造性劳动，包括相关知识的创造性应用．

推论1ACP存在非负的稳定解.

在定理2中，我们证明了算子A+E的所有谱点除虚轴上0点外均位于左半复平面.同时P*是算子A+E的0本征值的0本征向量，故P*是非负的，所以P*是ACP的非负的稳定解.

定理3令P*是算子A+E的0本征值的本征向量且满足||P*||=1，取Q=(1,1,1,1,1,1)，则ACP的时间非负依赖解P(x,t)，当时间t趋于无穷时趋于系统的非负稳定解P*：

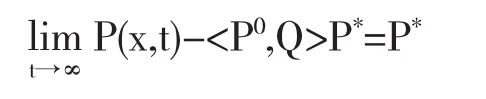
其中P0是方程初始值.

由[9]可知，定理3的结论是强连续半群稳定性的一个结果.故此，我们就验证了A+E的0本征值的本征向量P*是ACP的唯一非负的稳定解且满足

参考文献：

〔1〕Gupta S M.Stochastic analysis of systems with primary and secondary failures[J].Microelectronics Reliability,1995,35(1):65-71.

〔2〕Gupta P P,Tyagi L.MTTF and availability evaluation of a two-unit,two-state,standby redundant complex system with constant human failure[J].MicroelectronicsReliability,1986,26(4):647-650.

〔3〕徐厚宝,柳合龙,于景元,等.具有临界和非临界操作错误的人机系统的渐近稳定性[J].系统科学与数学,2005,25(5):513-524.

〔4〕柳京爱,郑福.具有四类故障可修系统解的存在唯一性[J].数学的实践与认识,2004,34(12):133-136.

〔5〕GupurG,LiXZ,ZhuGT.Functional Analysis Method in Queueing Theory[M].Research Information,Hertfordshire,2001.

〔6〕马艳英,李秀珍,乔兴.具有四类故障可修复系统非负弱解存在唯一性[J].吉林工程技术师范学院学报,2008,24(4):78-80.

〔7〕云鹏,凯院,仲.矩阵论[M].西北工业大学出版社,2006.

〔8〕张恭庆,林源渠,郭懋正.泛函分析讲义[M].北京：北京大学出版社,1990.

〔9〕Lyubich Y,V?P.Asymptotic stability of linear differential equations in Banach spaces[J].Studia Mathematica,1988,88(1):37-42.