奇解的判别法

布仁满都拉

（赤峰学院　数学与统计学院，内蒙古　赤峰　024000）

对于某些微分方程，存在一条特殊的积分曲线，它并不属于这方程的积分曲线族，但是，在这条特殊的积分曲线上的每一点处，都有积分曲线族中的一条曲线和它在此点相切，在微分方程里，这条特殊的积分曲线所对应的解称为方程的奇解.

若一个微分方程它有奇解，怎么求它的奇解是本文主要讨论的问题.

判别微分方程奇解时，我们常用P-判别曲线法、C-判别曲线法.P-判别曲线法、C-判别曲线法，都是分别先求出P-判别曲线、C-判别曲线，再验证所求曲线中的某一支是微分方程的解，如果是微分方程的解，也不一定是奇解.但在求微分方程的奇解时，通常会采用这两种判别式.

1　奇解的定义

定义1[1]设在平面上有一条连续可微的曲线Γ，如果对于一点Q∈Γ，在单参数曲线族V(x,y,C)=0中都有一条曲线和它在Q点相切，其中C是参数，则称曲线Γ是曲线族V(x,y,C)=0的包洛.

定义2[1]设一阶微分方程有一特解Γ：y=φ(x)，如果对每一点 Q∈Γ，在 Q点的任何邻域内方程有一个不同于Γ的解在Q点与Γ相切，则称Γ是微分方程的奇解.

2　P-判别曲线法

定理1[2]设函数F(x,y,p)对x,y,p是连续的，而且对y和p有连续的偏微商F′y和F′p，若函数y=φ(x)是微分方程的一个奇解，则奇解y=φ(x)满足一个称之为P-判别式的联立方程

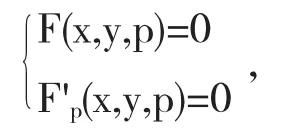
或(从中消去p)与其等价的方程Δ(x,y)=0,(x,y)平面上决定的曲线称为P-判别曲线.

例1求方程的奇解.

解从

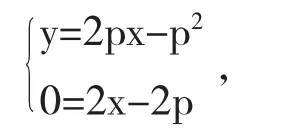
消去p,得到P-判别曲线

因为求得原方程的参数形式的通解为

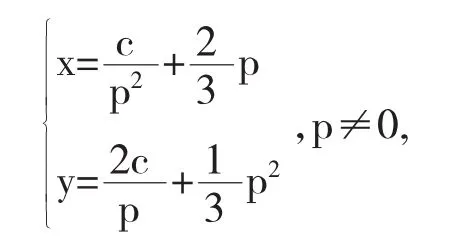
当p=0时，直接推得y=0也是方程的解.

但y=x2不是方程的解，故此方程没有奇解.

例2求方程的奇解.

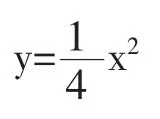
因为原方程的通解为

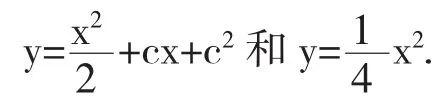
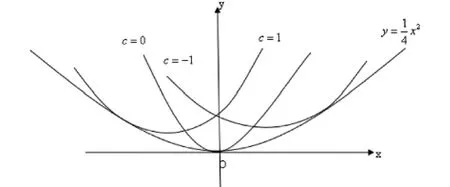
3　C—判别曲线法

定理2[3]设微分方程有通积分V(x,y,C)=0，又设积分曲线族V(x,y,C)=0有包络为：y=ø(x)，则奇解 y=ø(x)满足如下 C- 判别式

或（从中消去C）与其等价的方程Ω(x,y)=0.

例3求方程的奇解.

解易求得方程的通解是

对C求导，得-2(x-c)=0，

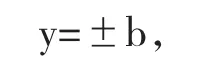
验证它显然是解，又是通解一圆族的包络线，因此y=±b是奇解.

定理1和定理2都是判断微分方程奇解的必要条件.也就是说，用P-判别曲线法和C-判别曲线法求出的解不一定是微分方程的解.如果是微分方程的解，也不一定是奇解.但在求微分方程的奇解时，通常会采用这两种判别式法.

参考文献：

〔1〕东北师范大学微分方程教研室.常微分方程[M].北京：高等教育出版社，2005.

〔2〕丁同仁，李承治.常微分方程教程[M].北京：高等教育出版社，2004.

〔3〕王高雄，周之铭，等.常微分方程[M].北京：高等教育出版社,2006.