基于随机森林方法的地震插值方法研究

徐凯，孙赞东

中国石油大学(北京)地质与地球物理综合研究中心，北京 102249

0 引言

在地震勘探中，采集资料的准确与否对勘探结果有着至关重要的作用。但是在地震资料的采集过程中，由于地形、实际采集方法等条件限制，采集得到的地震数据经常会存在坏道、死道、空道等情况，严重影响了后续的偏移解释等工作。地震插值是一种较为有效的解决该问题的方法。

地震插值主要有以下几种方法：(1)基于变换域的插值方法。该方法主要是将地震信号变化到其他域内进行操作，然后再反变换到时空域。主要有Radon变换，Fourier变换，曲波变换等方法。Fourier变换方法是将其变换到波数域进行道集重建。在波数域可以实现五维插值的效果[1-3]。Sacchi[4]等在反演的思想下实现了五维插值的方法。曲波变换是小波变换的另一种形式，可以较好的描述地震数据的稀疏特性，可以采用压缩感知的方法来进行插值[5-7]。(2)基于预测滤波的插值方法。Spitz[8]在f-x域实现了基于预测滤波的插值方法，Claerbout[9]在此基础上研究了t-x域的预测误差滤波地震插值方法，实现了含假频的数据重构。上述传统插值方法都是基于较为复杂的数学变换或者波场重构理论，计算较为繁琐，而且在变换重构过程中需要多种近似，难以精确预测缺失地震道的真实情况。

机器学习方法在地球物理中得到了广泛的应用。目前应用主要集中于地震属性预测领域[10-14]。在地震插值领域，机器学习方法应用较少。由于地震道缺失问题可以看作是一个随机的、非线性的数学问题，而且地震道插值主要用了周围几道的的信息，所以本文尝试采用机器学习中有监督学习，从局部规律学习的角度出发来进行缺失道数据的补全处理。有监督学习是一种从标签化训练数据集中推断出抽象函数的机器学习技术，常见的算法包括决策树、神经网络、支持向量机、梯度下降树和随机森林等算法。各类算法各有利弊，其中随机森林算法是由Brieman于2001年提出的一种集成机器学习算法[15]，可用于解决高维非线性的分类预测、回归预测与特征选择。它是Bagging集成学习算法[16]的改进版本，大量实践证明随机森林能够有效解决高维非线性问题，是目前阶段被广泛使用的一种机器学习算法[17]。

本文首先介绍了基于机器学习思想的随机森林回归预测方法。从理论上推导了本文方法的可行性。随后在机器学习的思想下，以无缺失道为学习样本集，补全缺失的地震数据。最后将该方法分别应用于模型资料与实际资料，验证了该方法的正确性与有效性。

1 基于随机森林的缺失道补全

1.1 随机森林回归预测算法

随机森林回归预测算法是一种集成大量随机决策树模型的集成学习算法[13]，其基础是CART回归决策树算法[14]。对于y=F( X)，其中X={x1, x2... xP}型的回归问题，CART回归树算法通过优选分割变量及其阈值，将原始的P维输入空间递归分割为有限个子空间。在具体的递归分割过程中，假设当前父节点所对应子空间为XC，记对于第i个输入变量xi阈值为的分割为S()，则S()等效于将其分割为左右两个节点，设左边节点对应子空间XL，右边节点对应的子空间为XR，分割规则可表示如下：

对于回归问题CART决策树将遍历XC中P维输入x1, x2... xP中每一个潜在的分割S()，优选最佳分割使得“不纯度”I()最小，其中I()可表示为：

(1)当前父节点中所有样本P维特征均一致；

(2)当前父节点中样本个数小于给定最小叶子节点样本个数；

(3)当前父节点中样本的y值方差小于给定方差阈值。

条件满足时，停止递归分割并将当前父节点设置为叶子结点。在完成递归分割后，所生成的CART决策树等效于将整个样本空间X分割为X1, X2... XS，并以二叉树的形式存储分割逻辑。在预测时，CART决策树取每个空间内的样本在预测变量y上的均值作为该子空间内的预测值，建立回归预测函数：

式中，I为脉冲函数，E为期望值。

综上所述，可见CART可通过对训练样本的学习拟合出一个分段常数函数，该函数能够在一定程度上有效表示原始训练样本中的潜在统计关系，但往往过于粗糙且不稳定。对此Brieman利用集成学习的思想，通过对原始样本集进行Bootstrap抽样获取N个样本子集，而后在这N个样本子集的基础上分别构建CART回归树，在预测时取这N个CART回归树的预测均值作为最终的预测结果，这种方法被称之为Bagging集成，它能够在一定程度上克服单个CART预测模型的弊端。

而后Brieman通过数学证明和数据实验表明，在保证Bagging集成模型中每棵树的有效性同时，使得每棵树间的差异越大则最终的集成预测效果越好。在此思路的指导下，Brieman通过对决策树的生成过程中引入更多随机性来提高每棵树间的差异。该算法被称之为随机森林算法，其算法框架如图1所示，其随机性的引入通过两方面进行：

(1)与Bagging集成相同，随机森林首先对全部样本集进行Bootstrap抽样，生成一系列随机样本子集，在各样本子集的基础上进行决策树的构建。

(2)在节点分割过程中，与CART决策树遍历所有输入的所有潜在分割不同，随机森林中随机决策树仅在K个随机抽选的特征子集中进行优选来分割当前节点。

根据上述方法构建出的随机决策树在保证每棵树具有相当的准确性的同时，使得树与树之间的差异性足够大。较之于Bagging集成随机森林模型具有抗噪性好、有效避免过拟合且得到的函数关系更为平滑。大量实践证明，随机森林回归预测算法能够有效学习样本集中的高维非线性统计关系，因此本文主要基于随机森林算法学习缺失道集临近道各点振幅间的高维非线性统计关系，据此进行缺失道的补全。

1.2 从局部学习角度进行缺失道补全

目前常用的地震插值方法虽然易用性较高，但是存在以下问题：

第一，各类插值方法本身具有其模型假设，例如三次样条插值方法假设相邻数据点间满足三次多项式关系，而克里格类插值方法假设整个剖面上的数据点满足二阶平稳假设，当实际资料中的地震数据与这些假设偏差较大时，强行基于这些插值方法进行缺失道补全，将造成不可避免的计算误差。

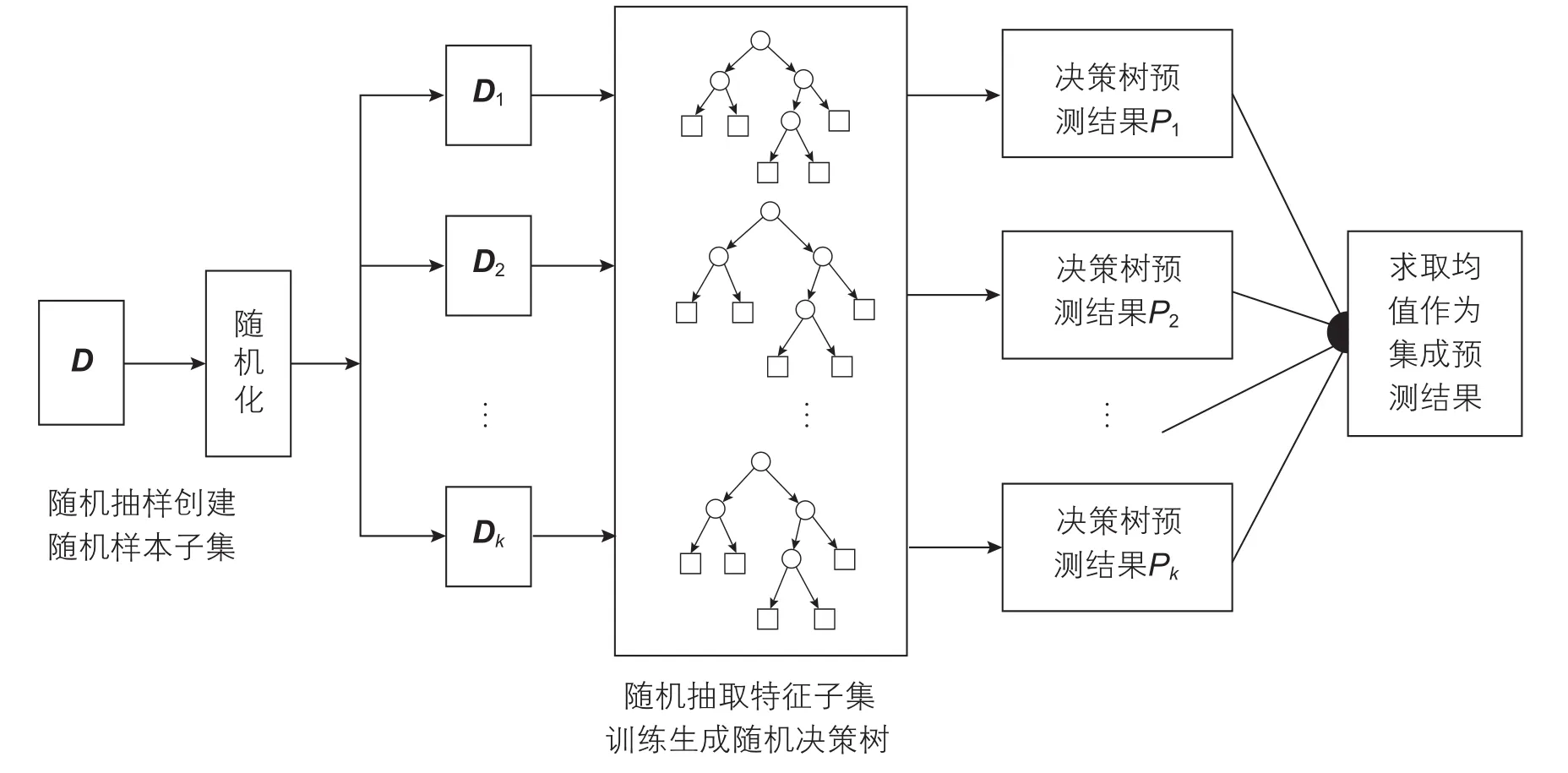
图1 随机森林回归预测算法示意图Fig. 1 A schematic diagram of random forest regression prediction algorithm

第二，插值方法完全忠实于所给出的数据点(插值得到的一维曲线、二维曲面一定过各数据点)，对于噪音干扰较大的数据无法保证各数据点上数据测量结果的准确性，完全忠实于所有数据点进行插值会把采集误差、随机噪音等引入到插值结果中。

此外，作为一种全局方法，通过插值方法进行缺失道补全将依赖整个道集剖面中的所有数据，而实际上对缺失道某一时间点振幅补全结果产生实质影响的仅仅是临近道临近时间范围内的数据点。考虑到对于缺失道Ti的给定时间点t处的振幅Ai,t，在整个共炮集剖面中与其具有较强相关性的数据点仅是Ti的临近道Ti+n的t+m范围内数据点的振幅Ai−n,t−m,…,Ai,t,…,Ai+n,t+m。本文所提出方法的基本思路是以Ai,t为学习目标，而以Ai−n,t−m,…,Ai,t,…,Ai+n,t+m等为输入，基于随机森林算法基于机器学习过程，根据未缺失部分数据建立回归关系Ai,t=F( Ai−n,t−m,…,Ai,t,…,Ai+n,t+m)，而后将回归预测函数F( x)应用到缺失道位置处，基于缺失道的临近道数据对其进行补全。

对于真实的地震数据，数据道的确实情况可分为两种，一种为单道缺失(如图2(a)中所示），对于这种情况缺失道左右两侧的临近道均可获取；另一种情况则为连续缺失(如图2(b)中所示），这种情况下仅有最边缘缺失道的左侧或者右侧的临近道可确定。针对这两种情况，分别采用不同的策略进行缺失道补全。

对于单道缺失的情况，以同一道集剖面中未缺失数据道为基础，分别以Ti道的t时间点处的振幅Ai,t，以及Ti左右Ti±2的t±5范围内的共44个数据点的振幅Ai±2,t±5等构建机器学习样本集，在此样本集的基础上使用随机森林方法，通过机器学习得到统计关系Ai,t=Fm(Ai±2,t±5)。其中m代表缺失道两侧。同时考虑到这一统计映射关系可能随着空间位置(道号i)和时间发生变化，因此同时将道号i和时间t也纳入输入空间之中，所得到的Fm实质上为Ai,t=Fm(Ai±2,t±5,i, t)。对于单一缺失道Tj时间点为t处的振幅，可通过将其所在左右临近道t附近44个点的振幅Ai±2,i±5道号i、时间t带入Fm按照Aj,t=Fm(Ai±2,t±5,j, t )计算得到。

对于连续缺失的情况，由于无法获取各道左右临近两道数据，无法按照回归预测函数Fm(x)进行预测，对于这种情况采用递推方法进行预测补全。以最左侧缺失道的补全为例，按照与单道缺失相同的方法，以同一道集剖面中未缺失数据道为基础，分别以Ti道的t时间点处的振幅Ai,t，以及Ti左侧Ti−1,Ti−2,Ti−3,Ti−4,范围内的t±5范围内的共44个数据点的振幅、道号等构建机器学习样本集，在此基础上利用随机森林算法学习得到Ai,t=Fl( Ai−1…5,t±5,i, t )统计关系，其中l代表缺失道左侧。对于连续缺失的最左侧道Tj，带入Aj,t=Fl( Aj−1…5,t±5,j, t)计算其各点振幅，而后将预测的到的T*j作为未缺失道，按照同样的方法计算Tj+1道各点的振幅。以此类推得到连续缺失各道的振幅响应。

图2 单道缺失和连续缺失情况下的输入点分布示意图Fig. 2 A schematic diagram of input point distribution for single trace loss and continuous loss

与此同时，以同一道集中未缺失数据道为基础，分别以Ti道的t时间点处的振幅Ai,t，以及Ti右侧Ti+1,Ti+2,Ti+3,Ti+4范围内的t±5范围内的共44个数据点的振幅、道号等构建机器学习样本集。在此基础上利用随机森林算法学习得到Ai,t=Fr( Ai+1…5,t±5,i, t)的统计关系，其中r代表缺失道右侧。按照同样的方法从最右侧缺失道开始，从右至左预测各道振幅。最终，取从右至左和从左至右个点两个振幅预测结果的均值作为最终预测结果。

2 方法应用分析

我们将本文方法分别应用于正演模型资料与r1区域的实际采集资料，分析预测结果，验证该方法的正确性与有效性。随机森林主要的算法参数包括：(1)随机树的个数，(2)随机特征子集的大小，(3)叶子结点中最少样本点个数。一般而言树越多越好，但过多的随机树会带来巨大的计算时间，权衡利弊后，选择使用500棵随机决策树构建随机森林。而在树的生长过程中，考虑到46个随机特征子集输入中可能存在无效输入，通过从1到46逐个尝试，最终确定取23个随机特征子集预测时效果最佳。而叶子结点中最少样本点个数往往取决于样本集中的噪音强度，考虑到地震数据中不可避免的存在测量误差，为提高机器学习预测模型抗噪性、防止过拟合，最小叶子节点样本个数不应太小，在本文的实验中将其设置为20。

2.1 正演模拟数据应用验证

首先将本文所提出方法应用到正演模拟数据上来验证方法的正确性。地层模型采用的是Marmousi模型。该模型里还有较多的断层、背斜、尖灭等地质情况存在，可以较好的验证该插值方法在复杂地质条件下的插值效果。对于给定地层模型，通过交错网格正演方法得到各道的波形记录(共100道，每道以2 ms为采样间隔，如图3(a)中所示），然后人为将第10、20、30、40、50、60-63、80-85道数据设置为缺失道(在图3(a)中使用虚线标出），而后利用在前文中所提出的方法，根据缺失道之外的各道数据构建机器学习样本集，得到回归预测函数Fm(x )、F1( x )和Fr( x)。据此对人为设置为缺失的道进行补全，补全结果在图3(b)中用红线标出。图3(b)中看出该方法能较完整的补缺道集。对于10、20、30、40等单道来说，该方法得到的补全道同相轴的连续性较好,与周围各地震道保持了连贯性。振幅的相似性较高，与周围各道保持一致。对于60-63、80-85各道的连续缺失来说，该方法也能较好的补全连续缺失道。从图中可以看出，补全连续缺失道中的第2道和第3道的振幅依然饱满，与前道相似度较高，同相轴连续性极佳，与单一缺失道的补全基本没有区别。

图3 正演数据模型及数据补全效果Fig. 3 Forward modeling data interpolation result

图4 单道振幅对比图Fig. 4 Single channel amplitude contrast diagram

为了测试该插值方法的保幅性，本文又抽取了第10、20、30、40、50、60、80、85道做单道振幅对比。由于这几道是人为设置缺失的，其真实模型振幅是可通过正演模拟得到的，因此可通过对比这些道的正演波形和补全波形，从而验证补全波形的正确性。图4中分别为第10、20、30、40、50、60、80、85道的正演波形(红色)和补全波形(蓝色)。从图中可以看出，除去在振幅非常强的波峰和波谷处存在差异外，正演波形和补全波形整体而言非常相似，各层振幅能量均衡，补全道与正演值匹配性较好。对于单道缺失跟多道缺失的第一道来说，本方法预测的振幅值在0.13左右，而真实振幅值在0.15左右，误差在10%左右。对于多道缺失的最后一道来说，预测值与真实值误差变大，大约在30%左右。但是振幅形态分布、波峰波谷位置保持一致，有效的证明了本方法的适用性。此外，搜集第10、20、30、40、50、60-63、80-85道上各点正演波形和补全波形振幅值，以正演波形的振幅值(真实幅度)为X轴、以补全波形的振幅值(预测幅度)为Y轴绘制散点图如图5所示。可以看出在幅度为(-0.2,0.2)范围内的数据点，真实幅度和预测幅度的点基本处于Y=X的对角线上，而对于幅度大于0.2的点还是存在着一定的偏差，这是因为决策树的预测本身为局部均值，而随机森林又为多颗决策树的估计均值，对于振幅过高的波峰和波谷将带来一定的平滑作用。但整体而言对于数据较为密集的区域，两者之间一致性非常高，整体相关系数R2可达0.906。

图5 各道波形真实幅度与预测幅度对比分析图Fig. 5 Comparison of real amplitude and predictive amplitude

众所周知，噪音是地震采集资料中不可忽视的一个重要影响因素。为了测试本算法的抗噪音能力，本文将模型数据加了20%的白噪，随后对再进行插值测试，如图6(a)所示。从图6(a)中可以看出，加噪音的插值结果与无噪音的补全结果基本一致，且与原始道集相似性高。图6(b)与图5相似，也是各道波形真实幅度与预测幅度的对比分析图。从图中可以看出，相关系数有一定的减少，但是整体形态变化不大，说明有噪音情况下的插值结果与真实值较为接近，可信度较高，证明了该方法有较好的抗噪性。

2.2 实际资料数据处理

图6 加噪音后的补全剖面与振幅散点图Fig. 6 Interpolation section and amplitude

同时本文将该方法应用于工区中的叠前采集数据，首先考虑对工区中无缺失道数据进行人工缺失，对比利用该方法得到补全道集与真实道集间的相似性，验证方法的有效性。将r1剖面(如图7(a)中所示）中的第10、70-75道人为设置为缺失道(如图7(b)中所示），而后按照前述方法以未缺失道部分数据为基础对第10、70、72道这三道进行补全，补全效果如图7(c)中所示。对比图7 (a)中和图7 (c)中剖面可以看出在人工缺失道位置处二者差别很小，在能看到同相轴区域，补全道能较好的延续同相轴走势，且从图中能直观看出振幅能量较强，图像的一致性较好。针对连续缺失的情况，如第70-75道,该方法也能较好的补全缺失道集，保持同相轴的连续性。

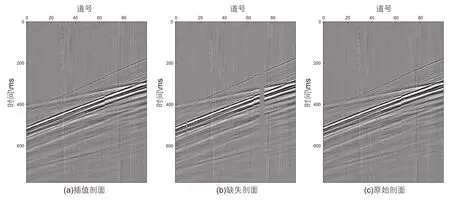
图7 人工缺失道集剖面补全效果Fig. 7 Real data interpolation result

图8 人工缺失道补全波形与真实波形对比图Fig. 8 Single channel amplitude contrast diagram

图9 缺失各道波形真实幅度与预测幅度对比分析图Fig. 9 Comparison of real amplitude and predictive amplitude

为了测试该方法的保幅性，本文抽取了10、70、72三道进行单道对比。在图8中将这三道的真实波形(红色)和预测补全波形(蓝色)进行对比，并以三道数据原始波形振幅为X轴、预测波形振幅为Y轴绘制散点图(图9)。从图9中可以看出，由于受真实数据中噪音和波形的复杂性影响，真实波形和预测波形间的一致性略逊于正演剖面数据，但二者之间的波形相似性依旧很高。无论是反射较强的区域还是反射较弱区域，补全道的振幅能量与真实资料较为一致，振幅大小也较为相似。对于单道缺失跟多道缺失的第一道来说，本方法预测的振幅值在50左右，而真实振幅值在40左右，误差在20%左右。对于多道缺失的最后一道来说，预测值与真实值误差变大，大约在40%左右。但是振幅形态分布、波峰波谷位置保持一致，有效的证明了本方法的实用性。

从图9中可以看出各点基本处于Y=X的对角线附近，以相关系数来定量评价二者相似性，原始波形振幅和预测波形振幅之间的整体相关系数R2可达0.899，已达到误差可接受范围内，说明本文所提出方法可应用于r1的实际地震资料插值。为了验证本文方法在插值方面的优越性，同时选用快速傅里叶变换的插值方法进行对比。图10为快速傅里叶变换方法的插值结果对比图。从图10中可以看出，快速傅里叶在单道缺失中效果较好，与随机森林方法类似，可以补全缺失道，并保证同相轴的延续性。但是连续道缺失情况下，该方法插值效果一般，同相轴连续性较差，缺失道异常现象明显。图11为单道振幅对比图，从图中可以明显看出，在第10道，70道时红色线与蓝色线吻合性较好，证明该方法对于单道缺失效果较为理想。第72道为连续缺失道的中间道，从图中可以看出，对于这种连续缺失道，快速傅里叶插值方法与理论值差别较大，波形相似性较低。单道缺失的振幅误差还能保证在20%以内，而多道缺失波形基本没有相似性，没有误差对比的必要。图12为预测振幅与真实振幅的散点图，从图中可以明显看出，真实振幅与预测振幅相差较大，散点图的趋势没有沿着对角线方向。通过与快速傅里叶变换插值的对比证明，本文提出的插值方法精确度更高。特别是对于连续缺失道插值，该方法能很好的保持同相轴趋势的连续性，较好的补全缺失道集。

图10 快速傅里叶方法插值结果Fig. 10 Fouries interpolation result

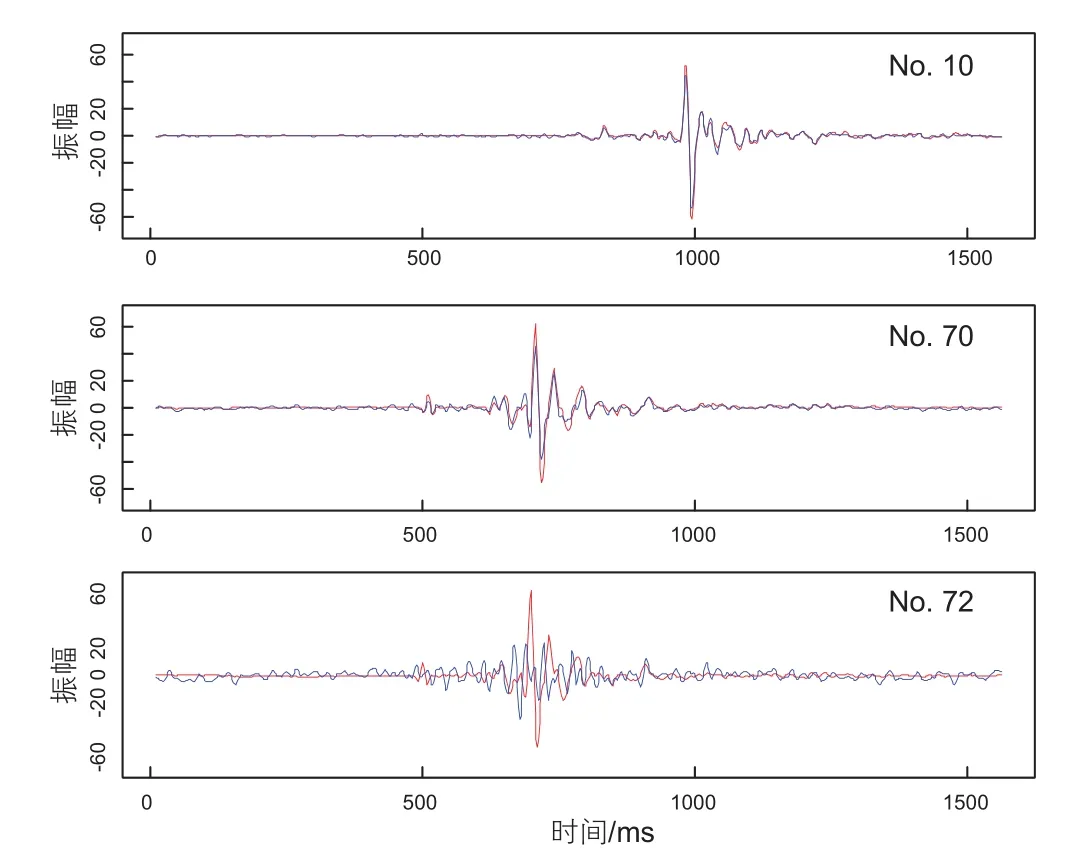
图11 快速傅里叶法缺失道补全波形与真实波形对比图Fig. 11 Single channel amplitude contrast diagram

图12 缺失各道波形真实幅度与预测幅度对比分析图Fig. 12 Comparison of real amplitude and predictive amplitude

3 结论与展望

目前针对地震插值的主要方法是将原始地震数据变换到其他域进行计算，随后反变换到时空域输出结果。不同于这一常用的方法，本文从利用机器学习进行地震插值的角度进行了研究。首先将无缺失道作为机器学习的样本集进行训练，学习各道各点之间的振幅关系。随后引入随机森林回归方法，预测缺失道的振幅时间关系，从而补全道集，得到一个较好的地震插值效果。本文采用了高随机性的多维随机森林回归预测方法，具有较好的抗噪性，而且能有效的避免过拟合现象。由于地震插值主要利用周围几个点的振幅值，所以本文引入了局部学习的方法，结果表明，该方法能够较好的补全缺失的地震道集，而且振幅准确，差异性较小。对于模型资料来说，基本可以完整补全缺失地震道，抽取的单道振幅表明，除了最强的波峰波谷处可能存在一定的误差，剩余波形基本能保持一致，且对噪音的压制作用较好。实际资料试算表明，该方法能够较好的补全缺失道，能保证同相轴的连续性，振幅的一致性，尤其对于多道缺失情况，该方法效果较好。相关函数表明除去波峰波谷，剩余波形相关性较高，证明该方法有较好的实用性。

但是该方法依然存在一定的局限性，主要表现为：(1)三维插值计算量太大，难以大规模应用。(2)无法与真实地下介质信息结合。所以本文下一步研究方向主要集中于以下两个方面：(1)三维资料插值需要使用124维数据。如何进行算法优化，利用先验条件(如上覆地层信息等)来约束插值过程，减少计算量是我们下一步研究的重点与难点。(2)由于不同地质条件对应的道集会存在一定的差异，所以本文方法针对不同地质条件得到更为精确的插值结果也是需要探索的内容。

[1] HAMPSON D. Inverse velocity stacking for multiple elimination [J]. Journal Canadian of Society of Exploration Geophysics, 1986,61(3):891-901.

[2] DANIEL T. A strategy for wide-azimuth land interpolation[C]. 77th Annual SEG Meeting Expanded Abstracts, San Antonio, 2007, 26:946-950.

[3] DANIEL T. Five-dimensional interpolation: Recovering from acquisition constraints [J].Geophysics, 2009, 74(6):123-132.

[4] SACCHI M D, GAO J J, STANTON A, et al. Tensor factorization and its application to multidimensional seismic data recovery[C]. 85th Annual SEG Meeting Expanded Abstracts, New Orleans, 2015, 4827-4831.

[5] 唐刚.基于压缩感知和稀疏表示的地震数据重建与去噪[D].北京:清华大学, 2010. [TANG G. Seismic data reconstruction and denoising based on compressive sensing and sparse Representation [D].Beijing: Tsinghua University, 2010.]

[6] 孔丽云,于四伟,程琳,等.压缩感知技术在地震数据重建中的应用[J].地震学报, 34(5), 659-666. [KONG L Y, YU S W, CHENG L,et al. Application of compressive sensing to seismic data reconstruction [J]. Acta Seismologica Sinica, 2012, 34 (5): 659-666.]

[7] 路交通,曹思远,董建华,等.基于稀疏变换的地震数据重构方法[J].物探与化探, 2013, 37(1), 175-179. [LU J T, CAO S Y, DONG J H, et al. A study of seismic data recovery based on sparse transform [J]. Geophysical and Geochemical Exploration, 2013, 37(1): 175-179.]

[8] SPITZ S. Seismic trace interpolation in the F-X domain. Geophysics [J]. 1991, 56(6): 785-794.

[9] CLAERBOUT J F, NICHOLS D A V E. Interpolation beyond aliasing by (t, x)-domain PEFs [C]. 53rd Annual EAEG Meeting ExpandAbstracts, Paris, 1991, 2-3.

[10] KADKHODAIE I A, REZAEE M R, RAHIMPOUR B H, et al. Petrophysical data prediction from seismic attributes using committee fuzzy inference system[J]. Computers & Geosciences, 2009, 35(12): 2314-2330.

[11] HUANG L, DONG X, CLEE T E. A scalable deep learning platform for identifying geologic features from seismic attributes [J].Leading Edge, 2017, 36(3): 249-256.

[12] SMITH T. Geobody interpretation through multiattribute surveys, natural clusters, and machine learning [C]. 87th Annual SEG Meeting Expanded Abstracts, Houston, 2017, 2153-2157.

[13] GUITTON A, WANG H, TRAINOR G, et al. Statistical imaging of faults in 3D seismic volumes using a machine learning approach [C].87th Annual SEG Meeting Expanded Abstracts, Houston, 2017, 2045-2049.

[14] LIN Y, GUTHRIE G, COBBLENTZ D, et al. Towards real-time geologic feature detection from seismic measurements using a randomized machine-learning algorithm[C]. 87th Annual SEG Meeting Expanded Abstracts, Houston, 2017, 2143-2148.

[15] BIEIMAN L. Random forest [J]. Machine Learning, 2001, 45:5-32.

[16] BREIMAN L. Bagging predictors [J]. Machine Learning, 1996, 24(2):123-140.

[17] WU X, KUMAR V. The top ten algorithms in data mining [M]. New York, USA: CRC Press, 2009.

[18] ZHOU Z H. Ensemble methods: Foundations and algorithms [M]. Boca Raton, FL: Taylor & Francis, 2012.

[19] BREIMAN L, FRIEDMAN J H, OLSHEN R A, et al. Classi fication and regression trees [M]. Belmont, CA: Wadsworth and Brooks,Monterey, 1984.